转发式干扰条件下LFM雷达的检测概率估计

田元荣, 王俊迪, 吴笑天

(1. 国防科技大学电子对抗学院, 安徽 合肥 230037; 2. 空军工程大学航空工程学院, 陕西 西安 710038)

0 引 言

通过电子对抗手段压制防空雷达在空中进攻作战和攻势防空作战中扮演着极其重要的角色[1-2]。随着雷达技术和电子对抗技术的交替进步,现代战场上投入的干扰装备和雷达越来越多,一部干扰机的干扰信号可能会进入多部雷达的接收机产生干扰效果。从雷达的角度来看,是一部雷达受到多部干扰机的干扰,有些干扰是专门针对该雷达释放的干扰,有些则是针对其他雷达释放的干扰。针对被分析雷达,本文称这两种干扰分别为有意干扰和无意干扰。在这种情况下,为了准确地评估干扰效果,首先需要精细地估算被干扰雷达在一部干扰机有意干扰和无意干扰作用下的检测概率[3-5]。

在经典的电子干扰理论中,对对方雷达压制的效果评估可通过干信比(jamming to signal ratio, JSR)是否大于固定的压制系数来表示,但是在实际应用中需要精确获取雷达的辐射功率等参数以估算JSR[6]。文献[7]通过矩母函数推导了异构环境下雷达实现恒虚警检测时的检测概率闭式表达,并对比分析了所提方法与纽曼-皮尔逊准则检测的结果。文献[8-9]讨论了只存在噪声干扰的条件下雷达检测概率的计算方式,并且在分析计算时假定到达判决环节的干扰信号功率已知。最新的研究主要聚焦在对环境杂波和单点假目标干扰的建模中,例如文献[10]将背景和目标建模为指数分布和韦布尔分布,文献[11]分析了符合高斯分布的目标检测概率的估计方法,文献[12]对比分析了韦布尔分布和对数正态分布杂波背景下目标的检测概率等。开展以上分析主要借助了分布函数、特征函数和矩母函数等随机变量的统计特性。

综上所述,绝大多数现有研究是从雷达使用方的角度出发进行分析,且假定干扰是针对被分析雷达而施放的有意干扰,对无意干扰如何影响雷达的目标检测能力还有待进一步探索。基于这一研究目的,同时考虑篇幅和典型性,本文以线性调频(linear frequency modulation,LFM)雷达为对象,重点分析其在利用一部干扰机利用转发方式产生的有意干扰和无意干扰作用下的检测概率估计问题。

1 LFM雷达目标检测模型

从信号流向的角度来看,一部LFM雷达对回波信号的接收处理主要包括天线接收、射频段处理、数字信号处理、目标判决4个环节[13],如图1所示。其中,目标判决一般根据恒虚警率(constant false alarm rate, CFAR)检测技术来实现,根据背景杂波的不同,CFAR检测有单元平均CFAR(cell averaging CFAR, CA-CFAR)、有序统计CFAR(order statistic CFAR, OS-CFAR)等多种选择。在现代雷达信号分析中,通常将射频段处理过程称为接收机,并且认为系统噪声主要由该过程中的模拟器件产生,噪声服从正态分布N(0,v2),噪声功率可表示为Pn=v2。如果忽略模拟器件的性能,仅从数字信号处理的角度来看,LFM雷达接收到的信号可以归纳为匹配滤波、相参积累、检波和非相参积累4个步骤。

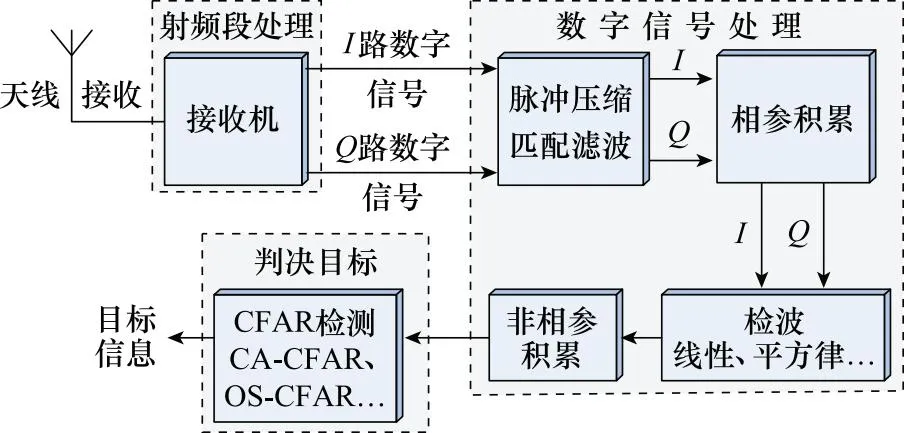
图1 LFM雷达信号处理流程图Fig.1 Flowchart of LFM radar signal processing

由于多个正态分布平方的和服从卡方分布,所以经过检波和非相参积累后,在CA-CFAR判决环节(见图2)中,被检测单元含有目标(H1)和不含目标(H0)的信噪比概率密度可表示为

(1)

图2 雷达CA-CFAR检测原理示意图Fig.2 Schematic diagram of radar CA-CFAR detection principle

式(1)中,Ia(·)和Γ(·)为修正的贝塞尔函数和伽马函数;Pto=CIPrtGtp/(v2Gnp)为CI个脉冲非相参积累后信噪比均值之和。式(1)中,H0情况下的概率密度推导过程是用v2Gtp对wI和wQ归一化,那么wI和wQ均服从N(0,1/2),CI个脉冲非相参积累即等效为2CI个N(0,1/2)非相参积累,参考卡方分布的定义可以得出上述表达式。

根据图2所示的CA-CFAR检测机制,用于估计检测门限变量Z的概率密度与H0条件下p(yt)的表达式类似,如下所示:

(2)

根据式(1)和式(2),LFM雷达对目标的检测概率和虚警概率可以表示为

(3)

2 LFM雷达对转发式干扰信号的接收增益

干扰信号对对方雷达产生压制效果的前提是干扰信号进入雷达的接收机,并影响目标判决的门限。如图1所示,雷达对干扰信号的增益主要体现在天线接收、匹配滤波、脉冲积累3个方面,这3个方面也可称为空域增益、频域增益和时域增益。

2.1 空域增益

实际作战场景中干扰机通常距离对方雷达较远,因此雷达天线对干扰机信号的接收增益主要体现在方位向上,假设简要作战态势如图3所示。

图3 雷达天线对不同方位向来波信号接收增益示意图Fig.3 Schematic diagram of radar antenna’s receiving gain for incoming wave signals from different directions

根据文献[14-15]给出的结论,雷达对干扰信号的空域接收增益可以近似为

Gsj(θj)=(1+q(2θj/θ0.5)2)-2Gst, |θj|∈[0,180°)

(4)

2.2 频域增益

h(n)=st(-n)*=exp(-j2π(kt/2)((Nt-1-n)Ts)2)

(5)

(6)

(7)

根据式(7),当n=Nt-1时,匹配滤波器输出可达到峰值Nt=τrfs=2τrBr,如图4(a)所示。

图4 目标回波和干扰信号的匹配滤波接收效果Fig.4 Matching filter receiving results of jamming signal and target’s echo signal

当信号调频范围为[-Br/2,Br/2]时,Nt=τrBr为信号的时宽带宽积,这与经典的雷达探测理论一致[13]。

干扰信号sj(n)经过匹配滤波器h(n)后,雷达接收到的信号为

(8)

(9)

近似效果如图4(b)所示。

综上所述,经过匹配滤波后,目标回波、干扰信号和高斯噪声的接收增益Gtp、Gjp和Gnp分别为

国际化、信息化、网络化、个性化成为21世纪的“标记”[1]。2014高等教育版的美国地平线报告预测，学生从知识的消费者转变为创造者，将是未来3-5年的趋势[2]。2014年全球举办了100余次创客大会，其中包括日本、中国、美国和意大利等国家[3]。创客精神和教育融合的新型教育模式——创客教育，在全世界得到迅速发展。

(10)

式(10)中,关于匹配滤波对高斯噪声的接收增益Gtp=Nt可参考一些经典书籍[13],这里不做赘述。

2.3 时域增益

根据图1所示的处理流程,干扰信号在时域上的增益主要由相参积累和非相参积累获得,由于转发式干扰主要依赖数字射频存储器(digital radio frequency memory, DRFM)实现,而且目前的DRFM几乎可以完美复制雷达辐射的脉冲信号。因此,雷达的相参处理机制对目标回波和转发式干扰信号的增益理论上是相等的,在工程实际中的差异可以忽略[14]。基于这一现状,在后续的分析和仿真中忽略相参积累增益,重点分析非相参积累的增益。雷达对进入接收机信号的非相参积累增益主要由被积累脉冲的个数决定,对于被检测单元,其非相参积累的个数等于雷达一视中相参处理周期的个数CI。

干扰信号对雷达目标检测的影响最终体现为在CFAR阶段抬高目标检测门限,因此非相参积累对干扰信号的增益主要体现为有多少干扰信号进入了CFAR的参考单元。如图5所示,干扰信号要进入雷达CFAR的参考单元,干扰持续时间必须覆盖雷达的CFAR单元,即图5上下两个脉冲序列中的阴影部分重合的比例。

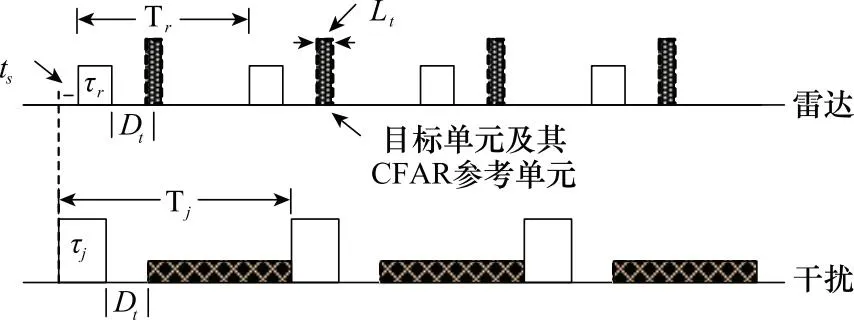
图5 雷达和转发式干扰机的脉冲时序示意图Fig.5 Schematic diagram of pulse timing of radar and repeater jammer

如图5所示,干扰覆盖目标回波和其CFAR参考单元的个数由时间差值ts决定。根据文献[16]的研究结果,如果ts服从均匀分布,那么目标单元及其CFAR参考单元被干扰覆盖的概率为

(11)

3 转发式干扰条件下LFM雷达的检测概率

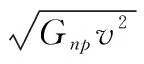
(12)

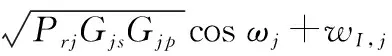
(13)

式中:Pjo=ρCIPrjGjsGjp/(v2Gtp)表示ρCI个含有干扰的脉冲非相参积累后的干噪比;ρ表示干扰与目标的重合率;Pto=CIPrtGtp/(v2Gnp)表示CI个脉冲总的信噪比。

(14)

同理,在干扰存在的条件下,用于估计CA-CFAR检测门限的变量Zj的概率密度可表示为

(15)

根据式(13)～式(15),在存在干扰的条件下,LFM雷达对目标的检测概率和虚警概率可以分别表示为

(16)

式(16)中,检测概率和虚警概率的公式非常相像,利用Marcum Q函数[17]进行推导,Pd,j的计算公式可进一步简化为

(17)

式中:g(m)为超几何函数的加权:

(18)

由于超几何函数具有性质a1F1(a+1,c,z)=(2a-c+z)1F1(a+1,c,z)+(c-a)1F1(a-1,c,z),所以:

(19)

式(19)中,β=1/(1+α)。同理,如果令式(17)中Pto=0,那么可以方便地计算出检测概率Pf,j。

针对式(17)中第二项无限累加的计算,由于Pjo关于m是单调递增的,所以随着m的增加,当Pd,j或者Pf,j的增幅小于需要的精度时即可停止,不需要无限累加。

4 实验结果与分析

4.1 基本设置

现代战争中,无论是空中突防战斗、攻势防空战斗,还是阵地进攻或者防御作战,单架干扰机在一次干扰中通常面临1～2部目标雷达的干扰[1-2]。为了验证本文所提转发干扰条件下脉冲压缩雷达检测概率估计方法的有效性,设定如下微缩版的场景进行仿真实验:一架电子干扰无人机(位于(6 km,0.4 km))掩护一架攻击飞机(位于(16 km,0 km))突破对方的防空雷达阵地,对方在(0 km,0 km)和(-1 km,6 km)阵地位置部署两部雷达,分别记为雷达1和雷达2。雷达1和雷达2对15 m2目标的最大探测距离分别为30 km和40 km,态势如图6所示。由于干扰机和雷达的天线俯仰宽度较宽(测高雷达除外),因此在图6中忽略了各参战目标的高度参数。

图6 一架干扰机掩护一架攻击机突防对方防空雷达态势示意图Fig.6 Schematic diagram of situation for a jamming aircraft covering an attack aircraft penetrating enemy air defense radar

由于干扰无人机体积较小,假设两部雷达的回波信号仅由大型的攻击机反射产生。通常情况下,干扰机的干扰波束较宽,实验设定干扰无人机在释放干扰时,雷达1和雷达2均能收到干扰信号。干扰机采用转发干扰方式进行干扰,转发的信号为雷达2辐射的信号。在这种态势下,本节的实验聚焦分析雷达1的检测概率,即转发式无意干扰对雷达1检测概率的影响。雷达1和雷达2辐射的信号样式均为LFM信号,且重频和脉宽固定,具体参数如表1所示。

表1 仿真中雷达的性能参数

雷达1判决目标采用CA-CFAR机制,虚警概率设为10-3,CA-CFAR的保护单元在被检测单元左右各设置1个。由于本文聚焦分析雷达1的检测概率,因此不对雷达2的性能参数进行设定,而只在表1中给出了其信号参数。值得说明的是,本文的目的是评估干扰机分别转发雷达1和雷达2的信号干扰雷达1的干扰效果,转发的干扰信号功率是相同的。

所有实验均在仿真软件上进行,为了便于表述,称式(3)和式(16)计算的结果为理论结果,称由所建立仿真雷达系统统计的结果为仿真结果。其中,仿真结果基于Matlab相控阵工具箱中提供的功能实现,仿真中雷达检测概率为独立仿真10 000次后目标被检出的次数与仿真次数的比值,不同仿真轮次中接收机混入的噪声独立。同理,虚警概率为超过门限的非目标单元个数与总的非目标单元个数的比值。

4.2 结果与分析

实验 1有效性分析

设置雷达1的CFAR参考单元个数为24,设置干扰机功率使得干扰信号出现在目标单元的JSR分别为0、0.05和0.3,被掩护目标(攻击机)RCS的平均值为从0.01 m2至25 m2均匀选取的60个值。统计雷达1的检测概率,结果如图7所示。其中,JSR=0意味着干扰机不释放干扰,此时雷达的检测概率和虚警概率由式(3)计算。

图7 雷达检测概率随RCS变化的曲线Fig.7 Radar detection probability changing curve with RCS

从图7可以看出,由式(3)和式(16)计算的理论结果变化趋势与仿真结果变化趋势一致,说明在本文提出的干扰条件下雷达检测概率估算方法是有效的。从图7还可以看出,无论干扰存在或不存在,由式(3)和式(16)计算的理论结果均高于仿真结果,主要原因为在计算干扰信号经过目标雷达的匹配滤波器时,忽略掉了LFM信号频谱中的菲涅尔波动,而是用矩形做了近似,加之回波信号距离旁瓣的存在(见图4),导致CFAR参考单元中的信号强度高于理论值,即判决目标时所用的Z值高于式(3)和式(16)中的Z值,从而降低了检测概率。相对于较大的干扰功率,为了保证虚警率恒定,菲涅尔波动对小功率干扰信号的影响更大。

影响理论结果与仿真结果差值的另一个因素是CFAR参考单元的个数R,保持其他实验参数不变,设置JSR分别取0和0.25,R分别取4、8、32和64,统计实验结果如图8所示。

图8 JSR和R取值不同检测概率随RCS变化曲线Fig.8 Curve of detection probability with RCS for different values of JSR and R

从图8(a)可以看出,随着R的增大,理论结果与仿真结果的差值在减小,并且差值减小的幅度同样在减小。这其中的原因为,如果匹配滤波对干扰信号的输出功率恒定,那么CFAR参考单元个数越多,对干扰功率的估计就越准确。除此之外,R越大,回波信号距离旁瓣越小,这也是一个原因。图8(b)中,JSR=0.25时,R=64的理论结果与仿真结果与R=4时差值比较接近;而当JSR=0时(即无干扰条件下),R=4的理论结果与仿真结果差值明显大于R=64对应的差值。

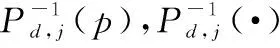
实验 2有意转发干扰和无意转发干扰的效果对比

为了探究有意转发干扰和无意转发干扰对雷达探测概率的影响,设置干噪比在[0,1.5]范围内均匀取50个样本值进行实验,统计干扰机转发雷达1的信号(LFM1)和雷达2的信号(LFM2)对雷达1的干扰时,雷达1的检测概率结果如图9所示。其中,雷达1在干扰机转发LFM1时,虚警概率的理论值等于Pf=(NfPd,LFM1+(Ng-Nf-Nt)·Pf,LFM1)/(Ng-Nt),Ng、Nt、Nf分别表示距离门、真目标、假目标的个数,对于本实验来说,真目标仅为攻击飞机,即Nt=1。Pd,LFM1和Pf,LFM1表示雷达1对干扰机转发自身辐射的信号(LFM1)形成假目标的检测概率和虚警概率,可以通过替换式(3)中的pto为pjo求得。

图9 干扰机转发不同雷达信号检测概率随JSR的变化曲线Fig.9 Curve of detection probability with JSR for jammer forwarding different radar signals

从图9(a)可以看出,当转发LFM1且JSR接近1时,检测概率突降到0,这主要是由于在CFAR单元中,当真目标和假目标的强度相等时,会导致或者目标和干扰信号同时被检出,或者同时都不被检出。影响该突变点的主要因素是α变化一个分辨率时所导致的检测率变化。转发LFM2时,检测概率突变的原因与转发LFM1时的原因基本相同,不同的是,此时CFAR参考单元中信号的和Z服从参数中心为Rpjo、自由度为RCI的非中心卡方分布,目标单元服从中心为pjo+pjo、自由度为2CI的非中心卡方分布。由于实验中设置的R(R=18)远大于2,所以当JSR不断增大(相当于pjo增大)时,Z的分布比目标单元中信号的分布更快地趋于平坦,因此也就更早导致检测率降到零。不难发现当R减小时,检测概率趋于突变到零需要更大的JSR,如图9(b)所示。图9中理论结果高于仿真结果的原因与实验1的分析相同。

另外,从图9还可以看出,为了达到同样的干扰效果,干扰机转发LFM2比转发LFM1需要更少的干扰功率。这二者之间的关系具有重要意义,因为在雷达对抗实际应用中,根据战前情报和战术编队通信,容易推算出被干扰的目标雷达接收机输出的信噪比、雷达脉冲描述字等信息,但是无法获得雷达接收机中的噪声功率,从而将导致干噪比pjo无法计算。而使用目标雷达和非目标雷达信号进行干扰时所取得的干扰效果关系,将为多雷达多干扰机场景下干扰资源分配等应用提供支撑。

5 结束语

准确估计干扰条件下雷达对目标的检测概率是现代战争中雷达对抗攻守双方的迫切需求。针对转发干扰条件下LMF雷达的检测概率估计问题,本文首先分别计算了雷达对干扰信号在空域、频域和时域上的接收增益,并进行了合理的近似;其次,将干扰存在下目标回波的概率分布建模为服从非中心卡方分布,并基于此给出了雷达的检测概率估计方法。实验结果和深入的分析表明,在一部干扰机的无意干扰下,本文给出的LFM雷达检测概率估计结果可作为实际雷达检测概率的上限,而且相比转发被干扰LFM雷达辐射的信号,在转发其他LFM雷达的信号时,干扰机可用较小的干扰功率实现相同的压制效果。虽然本文的实验结果证明了所提方法的有效性,但考虑的是转发式干扰一种样式,并且被干扰雷达也假定为LFM雷达。如何评估多干扰机、多干扰样式场景下的干扰效果,尤其是转发式干扰产生的密集假目标压制和宽带噪声压制共同作用于目标雷达后其检测概率如何估计的问题,将是后续探索的一个主要方向。