E-WID 三维拓扑关系计算方法与实现

杨国红，周晓光,2，贺鸿愿,2，侯东阳,2，李存志,2

1. 中南大学 地球科学与信息物理学院， 长沙 410083；

2. 自然资源部时空信息与智能服务重点实验室，长沙 410083

1 引 言

自然资源部办公厅2022 年《全面推进实景三维中国建设的通知》中称：“实景三维作为真实、立体、时序化反映人类生产、生活和生态空间的时空信息，是国家重要的新型基础设施”。其建设包括建立地上、地下、室内、室外等地理空间实体的三维结构及时空关系等（陈军等，2022）。三维拓扑关系作为最重要也是最基本的空间关系（Belussi 等，2020），是实景三维建设及三维（three dimensions，3D）地理信息系统（geographic information system，GIS）中三维空间数据质量控制（何建宁等，2022）、更新处理与空间分析（Emamgholian 等，2021；Salleh，2021；黄兰兰等，2022）的理论基础。

三维空间数据间的拓扑关系类型多样（曹全龙等，2023）。其无法一一存储，不同拓扑关系类型对应的冲突与更新等处理操作迥异，因此，需要用特定模型对其进行形式化区分，以便于计算机自动识别与计算（Egenhofer 和Franzosa，1991；陈军和赵仁亮，1999）。国内外研究针对这一关键问题开展了大量工作，如建立了三维4I（郭薇和陈军，1997）、9I（Egenhofer 和Herring，1990）、25I（Zhou 和Guan，2019）、K6N9-I（郭甲腾和吴立新，2008）和GA-based（Yuan 等，2014） 等模型。这些模型大多是基于二维4I 、9I 模型发展起来的，并存在一些不足，如对于复杂目标的适用性有限、区分能力不足等。另外，当前应用比较广泛的9I（3D）模型仅定义了三维简单目标间的拓扑关系，不能区分带通道（如带窗户的墙壁）或空穴（如带溶洞的地质体）等复杂目标间的拓扑关系类型，且9I（3D）模型只能区分八种简单体/体关系（其中只有一种相交关系），不能区分如图1（b）~（d）所示的三种常见拓扑关系。因此，贺鸿愿（2021）引入流形拓扑理论，将已有的 E-WID（ Euler-number-based whole-object intersection and difference）模型（Zhou 等，2013），拓展至三维空间，建立了适用于复杂目标且比现有三维拓扑关系模型区分能力更强的三维E-WID（3D）拓扑关系模型。拓扑关系在三维数据更新中具有重要作用。如图1（b）、（d）所示，灰色墙壁为室内新增墙壁，与原红色墙壁间都有交，但图1（d）新增墙B 穿过了旧墙A，一般为冲突。E-WID（3D）虽然能够区分如图1 所示拓扑关系，但目前尚缺乏其拓扑关系计算方法。

图1 主墙墙壁与隔墙墙壁间不同的拓扑关系示例Fig.1 Example of different topological relationship between a main wall and a partition wall

E-WID（3D）模型并不局限于单一的数据组织方式，但由于拓扑关系计算依赖于空间目标的几何数据，因此，计算的具体实现需借助特定的三维空间数据组织模型。现有代表性三维数据组织模型中，B-Rep模型在GIS 中使用最为广泛，且已被ISO、OGC（open geospatial consortium）和CityGML（city geography markup language）等组织所采用(Zhou 等，2013；吴立新和史文中，2005；樊文平等，2005)。其中, Nef多面体数据组织模型具有能够表达复杂目标（如带通道或空穴的体），对应的布尔运算结果可表示为闭集且可以保留低维的几何元素（如两体间交集的点、线与面片）等特点（Hachenberger 等，2007）相较于其他B-Rep 模型能更好地与E-WID（3D）模型结合。

综上所述，本文利用Nef 多面体3D 数据模型及对应的布尔运算算法，研究了三维E-WID 拓扑关系计算方法，其中，包括基于集合运算结果的空间组件构建、维度与欧拉数计算算法等，模拟实现了三维空间目标间的E-WID（3D）拓扑关系的计算。

2 基于Nef 多面体的E-WID(3D)拓扑关系计算总体思路

2.1 E-WID(3D)拓扑关系模型

E-WID（3D）拓扑关系模型引入流形拓扑对二、三维基本空间目标进行统一形式化定义，通过目标整体交/差结果的维数和欧拉数取值的不同来区分二元目标间的拓扑关系类型。E-WID(3D)模型的描述公式如下（贺鸿愿，2021）：

式中，fD为集合运算结果的维度取值，当结果为空或各组件纯为点（零维）、纯为线（一维）、纯为面（二维）、纯为体（三维）五种基本情形时，对应的取值分别为{–1,0,1,2,3}；当结果为点线混合、点面混合、点体混合、线面混合、线体混合、面体混合、点线面混合、点线体混合、点面体混合、线面体混合与线面体混合时，对应的取值分别为{4,5,6,7,8,9,10, 11,12,13,14}；fE为集合运算结果中各空间组件欧拉数的合计值，当结果为空时取值为0，整体取值范围为（–∞,+∞）。

2.2 E-WID(3D)拓扑关系计算总体思路

两空间目标间E-WID（3D）拓扑关系计算一般包括五个关键步骤。以图2 中的两简单体A和B为例，其计算步骤包括 ：①获取两空间目标的几何数据等； ②对两目标进行整体交/差集合运算；③构建满足E-WID（3D）模型中维度和欧拉数计算需求的交/差空间组件，如图2（b）中交集的非流形需分解为流形等；④依次计算各交/差组件的维度和欧拉数；⑤计算各集合运算结果的fD和fE取值并进行形式化表达与检验。

图2 两三维空间目标（简单体）间E-WID（3D）拓扑关系计算步骤示例“Dim（）”为组件的维数；“Eul（）”为组件的欧拉数；si 为交集组件；sd 为差集组件Fig.2 Example of the steps for calculating the E-WID (3D) topological relationship between two three-dimensional objects(simple monomers)

基于Nef 多面体的E-WID（3D）拓扑计算流程，如图3 所示。包括如下步骤：①读取三维空间目标A、B空间数据，并将其转换为Nef 多面体；②对两Nef 多面体A与B进行整体交/差集合运算；③构建交/差运算结果的拓扑组件；④依次计算各交/差组件的维度和欧拉数；⑤计算各集合运算结果的fD和fE取值；⑥将计算结果转化为式（1）中的描述矩阵。上述过程中，数据获取与格式转换、布尔运算、形式化结果转换与检验等的实现均相对简易，但两Nef 多面体整体间交/差集组件拓扑构建及其应欧拉数计算实现相对复杂。

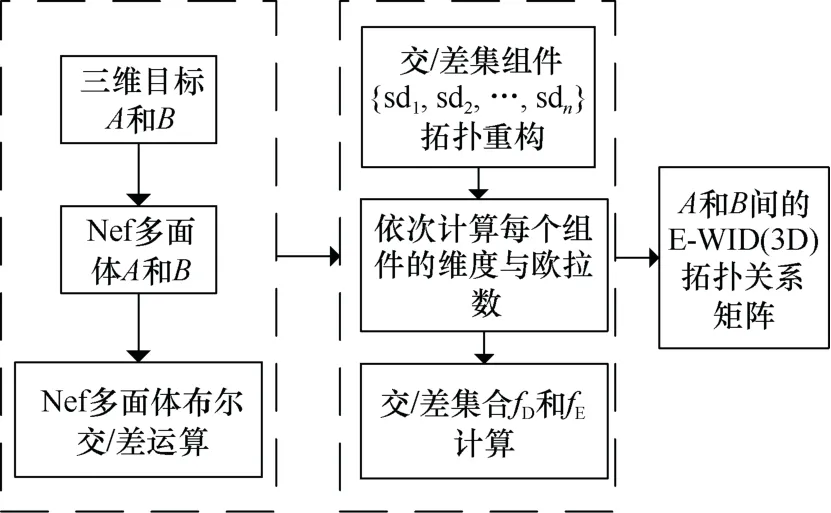
图3 Nef 多面体的E-WID（3D）拓扑关系计算流程Fig.3 Calculation flow of E-WID (3D) topological relations in Nef polyhedron

3 E-WID(3D)拓扑关系计算方法

由于三维空间目标的几何结构及相互关系的复杂和多样性，三维空间目标间的交/差集合运算的结果极其复杂多样。如图4 所示，两目标之间的交集可能同时出现点、线、面和体四种不同维度交集组件混存的情形；且这些交集组件之间不一定彼此相离，如图2（b）中（si1和si2相接）。而对两Nef多面体（空间目标）进行布尔运算后，其运算结果依然是将其整体作为一个Nef 多面体，并未自动将其分割成彼此独立的空间组件（流形）。因此，要计算两Nef 多面体间的E-WID(3D)拓扑关系，需先依据布尔运算结果对相应的交/差组件进行拓扑构建。

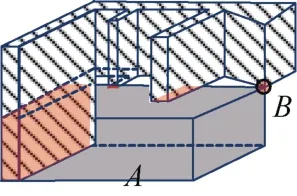
图4 两体体间具有不同维度的交集组件示例Fig.4 Example of intersection components with different dimensions between two objects

3.1 交/差组件的拓扑分析与构建

3.1.1 交/差组件集合的拓扑分析

在三维空间目标的交/差集合运算结果中，常见的空间对象点、线、面可以相对容易地识别（图5），因为它们具有明确的几何形状和位置。因此，获取它们的空间信息相对较为简单，无需进行过多的处理。通过识别和获取这些基本组件的空间信息，可以进一步分析和处理三维空间目标的交/差集合运算结果，以获得更复杂的拓扑关系和几何信息。

图5 交/差集合运算中Nef 多面体的基础情形Fig.5 Basic scenarios of Nefpolyhedron in set operations of intersection/difference

在集合交/差运算中，还会出现一些混合或相连的情况，包括：①线与面相连，如在图6（a）中，线l1与面s1相连；②线与体相连，如在图6（b）中，线l1与体sd1相连；③面与面相连，如在图6（c）中，面s1与面s2相连；④面与体相连，如在图6（d）中，面s1与体sd1相连。

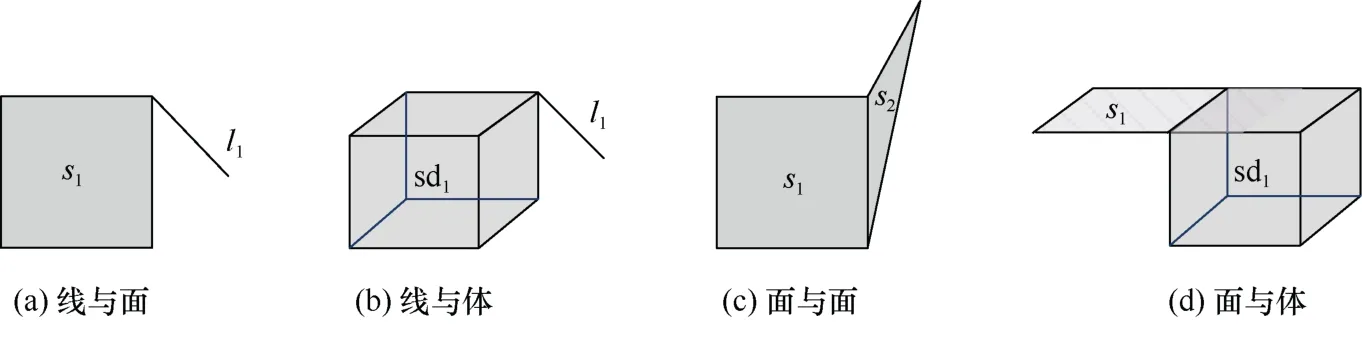
图6 集合运算结果中Nef 多面体的带悬挂情形Fig.6 Hanging situation of the Nef polyhedron in set operation results

在存在不同维度组件混合的情况下，需要对各个组件分别进行处理，并获取它们的拓扑信息。特别是当集合交/差运算中存在不同维度组件相连时，需要对不同维度的组件进行拆分，以便准确地分析和计算它们的拓扑关系。因此，在进行三维空间目标的交/差集合运算时，需要综合考虑不同维度组件之间的连接和相互关系，并采取相应的方法来处理和解决这些情况，以获得准确的拓扑信息。

以交/差运算结果中存在面与面连接或面与体连接的情况为例，可以判断面元素中的所有边是否都与其他面相连来获取交/差运算结果的拓扑信息。如果存在一条或多条边没有与其他面相连，则该面可以构成一个独立的二维交/差组件。例如，在图6（c）中，面s1只有一条边与相连面相连，其余的边没有与其他面相连；在图6（d）中，面s1也只有一条边与相连体的面相连，其余的边没有与其他面相连。因此，根据边界相连情况，可以确定s1为一个独立的二维交/差组件。通过识别和判断交/差运算结果中的二维面元素，以及其边与其他面的连接情况，可以将独立的二维组件确定出来，并进行相应的处理。这样可以准确地分析和计算三维空间目标间的拓扑关系。

在处理三维空间目标间的交/差集合运算结果时，处理空洞是一个关键问题。空洞是在交/差运算结果中存在未被填充或连接的空缺区域。在图7 中，简单面A与简单面B进行差集运算（AB）形成了一个带有空洞的平面目标（图7（b））。针对这个问题，可以利用简单面A与简单面B的交集运算结果（A∩B，图7（c））与目标进行判断。通过判断两个目标是否完全相同，可以得出目标B 是否包含于目标A，从而获取差集运算（AB）的空洞信息，并完成目标的构建。这种方法通过比较交集运算结果与目标本身的一致性，来判断空洞的存在与位置，从而实现对空洞的处理。这种处理方式可以提供更准确的空间信息，并为后续的拓扑关系计算提供可靠的基础。

图7 集合运算结果中Nef 多面体的带空洞情形Fig.7 Nef polyhedron with voids in set operation results

3.1.2 交/差组件的拓扑构建

在E-WID（3D）模型中，集合运算结果中的空间组件都对应着一个连通的紧致（闭集）的n流形，其中，n表示维度，取值范围为0≤n≤3。每个维度的组件都具有特定的几何结构和拓扑特征。以二维交/差组件的拓扑构建为例，为了从集合运算结果中识别并构建二维交/差组件，采取步骤如下。

首先，遍历所有的面目标，判断每个面是否与其他面相连。如果某个面有一条以上的边没有与其他面相连，则将其记录为一个二维组件。同时，当遇到带有空洞的平面时，也需要将其记录为二维组件并进行标记。其次，完成所有面目标的处理后，需要进一步判断构建的二维组件之间是否存在相连。如果存在相连的情况，需要将它们合并为一个更大的二维组件。此外，如果二维组件的连接形成了环形通道，需要将这些环形通道单独记录并进行存储。最后，通过这一系列步骤，完成二维交/差组件的构建。

判断规则一：设face 为集合运算结果平面集中faces 中的任意一个面，edge 为 face 的边，facei(i∈(1,n))为faces 中的面，edgej(j∈(1,n))为组成facei中的边，isolatedFace 为孤立面；如果edge 不等于facei.edgej，则face 为孤立面。

当使用CGAL 库中Nef 多面体表示时，可以通过检查Nef 多面体中的平面数据是否存在内环和外环，来判断是否存在空洞，可直接判断目标是否存在空洞，此处不再展开，二维组件是否相连与一维组件中的判断类似，下面是设计的规则。

判断规则二：设 isolatedFace 为孤立面，isolatedFacei(i∈(1,n))为孤立面isolatedFaces中的面，mergedFace(isolatedFace,isolatedFacei)为孤立面合并函数，edge 为孤立面的边；如果isolatedFace.edge与 isolatedFacei.edge 相等，则执行合并操作mergedFace(isolatedFace,isolatedFacei)。

基于二维组件的构建规则，使用交/差集合运算结果中的平面集合与平面边界集合，可实现二维交/差组件的构建，二维交/差组件的构建算法如图8所示。

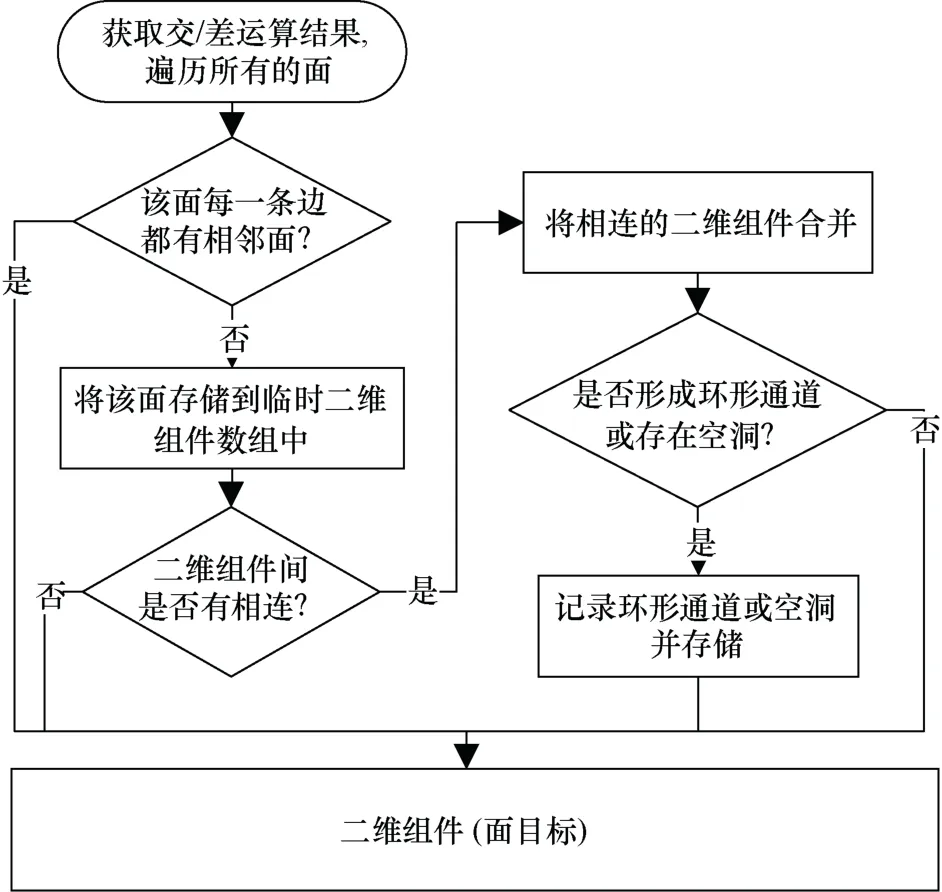
图8 二维交/差组件的构建算法Fig.8 Construction algorithm for 2D intersection/difference components

3.2 交/差组件的欧拉数计算

因为已构建好的各维度交/差组件均对应于一个流形（可胞腔剖分），所以其对应的欧拉数均可以通过如下计算（Lee，2010）：

式中，X为一个可胞腔（或三角）剖分的拓扑空间（或紧致流形）；n为X的维度；ai为X中i维胞腔（cell）的数目；Eul（X）为X的欧拉数。

对于零维、一维和二维的交/差组件，因均不包含三维胞腔，故其欧拉数可以统一通过式（2）的简化公式来计算，即

式中，V为对应组件经胞腔（或三角）剖分后的顶点数；E为边数；F为面数。

需要说明的是，虽然Nef 多面体数据中含有顶点、边和面等几何元素，但是这些元素并非胞腔剖分的结果，故需将对应的交/差组件先进行三角剖分，才能依式（3）计算。经剖分后，零维组件的边数和面数均为零，一维组件的面数为零。如图9（a）中零维组件A只含有1 个顶点，所以欧拉数等于1（V=1）；图9（b）中一维组件B含有3 个顶点和2 条边，所以欧拉数等于1（V–E=3–2=1）；图9（c）中二维组件C(简单面)含有3 个顶点、3条边和 1 个面，所以欧拉数等于 1（V–E+F=3–3+1=1）；图9（d）中二维组件D(带洞面)含有8个顶点、16 条边和8 个面，所以欧拉数等于0（V–E+F=8–16+8=0）。

图9 零维、一维与二维组件的欧拉数计算示例Fig. 9 Example of Euler number calculation for zero-dimensional, one-dimensional and two-dimensional components

由于三维交/差组件含有三维胞腔，但Nef 多面体只表达了其边界而忽略了其三维内部，所以在数据层面无法依式（2）或式（3）直接计算。需先将其边界进行三角剖分后，然后依式（2）计算其边界的欧拉数，最后依式（4）计算其最终的欧拉数（Lee，2010）：

式中，C为一个体目标；∂C为体的边界。

4 实验验证

为了验证所提出的三维空间数据间的E-WID（3D）拓扑关系计算方法的可行性，选取开源的Blender 构建实验数据，对系统的相关功能及相应拓扑关系的计算进行实验验证。验证了体/体关系19种，体/面关系18 种，面/面关系18 种，体/线关系11 种，面/线关系10 种，线/线关系10 种，体/点关系3 种，面/点关系3 种，线/点关系3 种，点/点关系2 种等基本拓扑关系类型（贺鸿愿，2021）计算的可行性。图1 中新建墙壁与原墙壁相交，存在冲突的两种情形，9I（3D）模型不能区分。而本文方法实现了自动计算，并且可以准确区分墙体打断、贯穿情形，如图10 所示。

图10 E-WID(3D)拓扑关系计算示例（A）为三维空间目标A；（B）为三维空间目标B；R(A,B)为两个三维空间目标在真实空间中的相对位置形态Fig. 10 Example of E-WID (3D) topological relation calculation

5 结 论

三维拓扑关系是最基本且最重要的空间关系，其计算实现是空间数据质量控制与处理等应用的基础。基于Nef 多面体数据模型及布尔运算，本文分析了三维空间目标间的交/差集合运算的结果，设计了E-WID(3D)拓扑关系模型中的交/差组件拓扑构建与欧拉数计算的方法，并研发了对应的原型计算系统，实现了三维空间数据间E-WID(3D)拓扑关系的自动计算。这为三维空间数据冲突检测与基于拓扑关系的分析等应用奠定了基础。

本文仅实现了基于Nef 多面体的三维基本拓扑关系计算方法，而三维地理信息表达方式多样，其他数据组织方法的三维拓扑关系计算可以参考本方法来实现或通过数据格式转换方式调用。另外，三维拓扑关系的细分及在三维数据质量控制、更新处理等方面的应用将是下一步的研究方向。