基于数值分析的电网精细化气象预报∗

梁 允，李 哲，孟高军，苑司坤，高 阳

(1.国网河南省电力公司电力科学研究院，河南 郑州 450052；2.南京工程学院电力工程学院，江苏 南京 211167)

随着电网规模的不断扩大和延伸，灾害性天气对电网安全运行的影响越来越大。同时，随着全球气候变暖、环流异常，灾害性天气产生的几率逐年上升，对电网安全运行的威胁不断增大。架空线路等输变电设备长期暴露于大气环境之中，其能否安全可靠运行与外部环境有密切关系，因此，精细化气象预报和输电线路的故障关联特性，提升电网运行可靠性水平一直是电力系统规划、调度运行、设备维修等工作所关注的重点[1－3]。严重的强对流大风、暴雨等偶发性天气均会影响输电线路运行稳定性，严重的气象变化会导致聚集性故障，对电力系统可靠运行危害极大。因此研究气象要素精细化预报，是避免电网发生气象灾害稳定运行的重点。

在气象因素对输电线路运行影响研究方面，文献[4]采用一种新的集合深度学习方法，对数值模式预报结果进行订正，并将其应用于数值模式预报误差通常较大的新疆乌鲁木齐城市群地区，文献[5]以气象数值模式数据为基础，设计风电功率预测系统的整体框架，基于高分辨率中尺度气象模式，利用卡尔曼滤波方法和实时观测资料对模式输出结果进行订正，文献[6]从气象对电网影响的周期性特征出发，采用统计算法计算全年纵向时间方向故障率分布函数，提出了一次基波傅里叶函数描述输电线路逐月故障率分布。文献[7]基于历史统计数据，分析天气随机变化特点，采用单项S－粗规律分析方法，建立F－分解规律分析气候对可靠性指标的影响程度，对输电线路故障率进行预测。文献[8]基于气象学原理和电网风险评估技术，建立电网台风灾害预警系统，综合处理台风信息和输电线路位置参数，给出输电线路的台风灾害分析和相应预警等级。文献[9]引入绝对值函数，以输电线路有功潮流与线路传输容量比值的绝对值定义输电线路负载率，建立一个恶劣天气条件下考虑电网载荷均衡程度及N－1 安全约束的防灾经济调度模型，文献[10]采用数据解析服务器分析采集气象数据写入数据库内，设计气象精细化数据电网灾害检测预警系统，实现电网系统运行脆性部位精确定位，并对气象灾害快速响应制定应急方案。

本文基于区域数值预报产品获得某地区未来三天的气象要素预报。采用动力降尺度技术消除具体地形和障碍物差值对气象数据的影响，通过历史样本统计分析，同时引入实时预报误差作为订正因子，利用回归统计方法，建立参考目标格点处的精细化订正模型，提升气象数据预报精度，并对气象数据及电网数据按照不同规则进行元素拆解，研究电力气象的数值分析整合，提高电网附近区域气象要素预报精度。

1 建立精细化气象预报模型

对于数值预报数据建立误差指标，采用经验统计方法对连续变量(风速、相对湿度和气温)进行检验，包括偏差检验(Bias Inspect，BIAS)和均方根误差(Root Mean Squared Error，RMSE)分析。

式中:Vobs，i代指INCA 预报的气象要素值，Vmodel，i代指WRF 预报的气象要素值，M表示统计样本个数，BIAS 为偏差检验值，RMSE 为均方根误差值。

依据气象要素平均绝对误差分析值分析气温、湿度、风速和风向等数值误差变化趋势，各要素的绝对误差变化值与奥地利国家气象局开发的短临集成分析预报系统(Integrated Nowcasting through Comprehensive Analysis，INCA)预报效果进行对比分析，数值预报基于高精度气象模拟软件(Weather Research Forecast，WRF)开发完成，WRF 模式中包括辐射过程、边界层参数化过程、对流参数过程、次网格湍流扩散过程、以及微物理过程等，利用卫星资料反演了土地利用类型、叶面积指数、植被覆盖度等产品[11]，在此基础上形成了可直接应用的数值模式。

降尺度预报采用微尺度模式中的网格化复杂地形风场动力诊断模式来进行，它利用质量守恒原理对风场进行动力诊断[12]，主要考虑了地形对近地层大气的动力效应、斜坡气流产生和障碍物阻挡效应，并采用三维无辐散处理消除插值产生的虚假波动。主要原理是，假设地形作用产生的垂直气流w与气流辐合辐散的关系为:

式中:f是模式网格平均风速，ht是地形高度，z是距地面的高度，k是与稳定度相关的衰减系数，表示为:

式中:N为布伦特－维赛拉频率。斜坡气流的速度采用经验的方法:

式中:Se是斜坡气流的平衡风速，Le是平衡尺度。障碍物阻挡的热力和动力效应用局地弗劳德数来衡量，局地弗劳德数表示为:

式中:Δht是障碍物的有效高度。如果局地弗劳德数小于等于临界弗劳德数且网格点风速有上坡的分量，则风向就调整为与地形的切线一致，风速不变；如果局地弗劳德数大于临界弗劳德数[13－15]，就不进行调整。

采用微尺度模式对两个重点实验区进行动力降尺度计算[16－18]，生成重点区域水平分辨率1 km 的未来3 天逐小时预报结果，预报要素包括气温、风速、风向、气压、湿度、降水等，预报高度层为地面、30 m、50 m 和70 m。对于地面气象要素而言，不同预报时效、不同区域存在不同的误差分布特征，在降尺度预报的基础上采用统计订正预报技术。

2 气象统计订正预报技术

首先利用地形订正的方法将气象站观测资料修正至临近模式格点处，得到参考目标格点处的观测和预报序列[19]；利用回归统计方法，建立参考目标格点处的精细化订正模型；利用反距离插值和地形订正相结合的方法，得到参考目标格点处的观测和预报序列，将精细化的订正模型拓展至模式预报的全网格[20]。

订正模型中引入实时预报误差作为订正因子，模型的业务运行稳定性受到一定限制；订正方案中大多引入全球再分析资料进行误差分析和预报订正，适用于时空尺度较大的区域范围预报，模式预报误差在时间上，随着预报时效的增长逐渐增大，可用预报信息减少，且预报误差具有显著的日变化特征，需要针对各个预报时次建立不同的订正模型；空间上相对湿度和气温的误差大小与海拔有密切关系，即海拔高的地方，误差也相对较大，这可能与该模式下参数设置比较粗糙有关，需要按照地形特征分区域建立不同的订正模型。

依据海拔差异的影响个例分析，气象站与模式格点的距离分别约为4 km 和7 km，距离较近，但气象站的海拔比模式最近格点处的海拔偏低约100 m，地形差异可引起较大的气温和相对湿度的变化。

在海拔订正基础上，利用回归统计方法，依次计算站点匹配的格点订正模型系数a和b；空间一致性检验及优化，即大于1 个气象站匹配同一个模式格点时，从数学的角度计算出多套统计订正模型，则对比模型相关系数、模型订正系数与周围临近格点的订正系数差异，选出最优且唯一的格点订正模型；全网格点订正模型:空间外推及平滑，最终建立了气象要素(地面气温和相对湿度)的精细化订正模式。

选取风速较大资料中质量较好的气象站为优选站，在每个优选站周围选取n个模式预报格点，将n个模式格点值插值到优选气象站点，按月份建立优选站点观测风速与模式预报风速的相关模型，用模式风速计算高精准预报值。每个模式格点周围选m个优选站，将m个优选站点位置的高精准预报值插值到模式格点，得到模式格点的高精准预报值。总计选出675 个优选站，模式预报格点为2 298 个。对于风速订正技术，首先选取风速较大资料中质量较好的气象站为优选站，在每个优选站周围选取n个模式预报格点，将n个模式格点值插值到优选气象站点，按月份建立优选站点观测风速与模式预报风速的相关模型，用模式风速计算高精准预报值。每个模式格点周围选m个优选站，将m个优选站点位置的高精准预报值插值到模式格点，得到模式格点的高精准预报值。

对于气温和湿度订正技术，模式预报误差在时间上，随着预报时效的增长，误差逐渐增大，可用预报信息减少，且预报误差具有显著的日变化特征，需要针对各个预报时次建立不同的订正模型；空间上相对湿度和气温的误差大小与海拔有密切关系，即海拔高的地方，误差也相对较大，这可能与该模式下参数设置比较粗糙有关，需要按照地形特征分区域建立不同的订正模型。因此，研究中将建立分月、分时次、分站点的精细化订正模型。

3 算例分析

以中部某省区域的数值预报为例对本文气象精细化数值分析技术进行验证，针对该地区气象要素，依据不同预报时效、不同区域误差分布特征，开展统计订正预报技术研究，以精细化专业气象预报服务的时空需求为目标，通过历史样本的统计分析，针对地面要素建立精细化的客观订正预报模型，以期提高面向专业服务的气象要素预报精度。

利用某省121 个国家级气象观测站和2 274 个区域自动气象站的逐小时地面观测资料，对模式近地层的气象要素(风速、气温和相对湿度)进行统计订正。某省地区自动气象站的分布如图1 所示，其中六要素指风速、风向、气温、相对湿度、气压和雨量，单要素为简易雨量站。时间范围取某地区14 个月数据。

其中圆形为国家站、三角形为六要素区域站、正方形为四要素区域站、圆点为单要素区域站。

数值模式逐小时预报资料:某省9 km 未来0～72 h 数值预报资料，时间范围为14 个月。首先利用地形订正的方法将气象站观测资料修正至临近模式格点处，得到参考目标格点处的观测和预报序列；利用回归统计方法和第2 节参考目标格点处的精细化订正模型；利用反距离插值和地形订正相结合的方法，将精细化的订正模型拓展至模式预报的全网格。

在海拔订正基础上，利用回归统计方法，依次计算站点匹配的格点订正前模型系数和订正后模型系数；空间一致性检验及优化，即大于1 个气象站匹配同一个模式格点时，从数学的角度计算出多套统计订正模型，则对比模型相关系数、模型订正系数与周围临近格点的订正系数差异，比选出最优且唯一的格点订正模型；全网格点订正模型:空间外推及平滑，最终建立了气象要素(地面气温和相对湿度)的精细化订正模式。

选择某省西部山区的某站点进行海拔差异影响研究，气象站见图1。可见，气象站的距离分别约为4 km，距离较近，但气象站的海拔比模式最近格点处的海拔偏低约100 m，地形差异可引起较大的气温和相对湿度的变化。

为了检验订正模型的预报效果，图2 和图3 给出了订正前后预报误差(以RMSE 为指标)的对比。

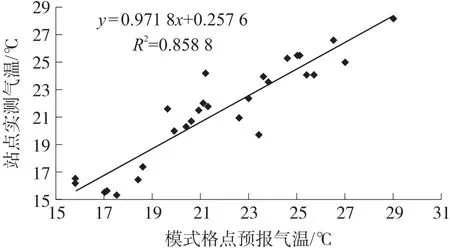
图2 地形订正前观测点与临近格点预报图

图3 地形订正后观测点与临近格点预报图

图4 中为地面湿度平面对比结果，图中<0 代表订正后的误差比订正前的误差小，图中可见订正模型在某省西部山区订正效果明显，东部平原地区也有正的订正效果，可见空间上订正效果理想。图5中的线条代表全区域平均的误差随预报时次的对比，图5 中虚线线条代表订正后的误差，实线为订正前的误差，横坐标代表未来1 个～73 个预报时次，图中可见，在未来73 个预报时次上，订正后的误差都普遍小于订正前。总体而言，地面气温的精细化订正模型在时间、空间上都具有明显的正效果。

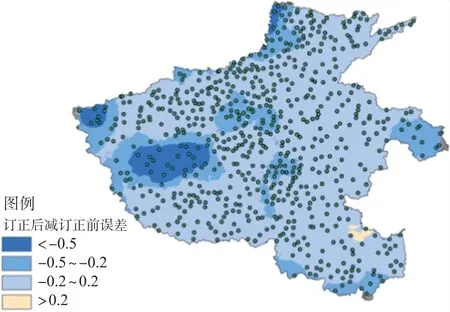
图4 地面气温平面对比图

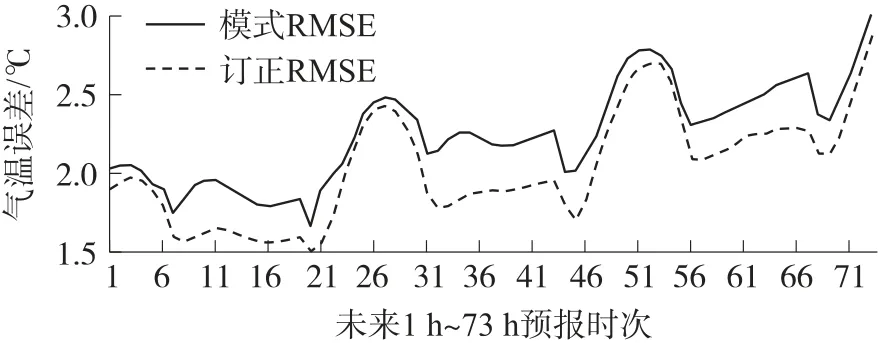
图5 地面气温误差对比图

与气温订正类似，下图中给出的相对湿度的订正效果，对比结果也显示出了较好的订正效果(见图6 及图7)。

图6 地面湿度平面对比图

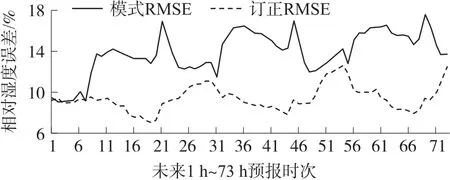
图7 相对湿度误差对比图

风速订正效果分析从总体特征、地理分布特征、时间分布特征三个角度来分析订正效果，具体分析如表1、图8 和图9 所示。

表1 某省不同预报时段气象站点风速统计结果 单位:m/s

表2 某省不同预报时段模式所有格点风速统计结果

图8 次气象站点风速绝对误差分布

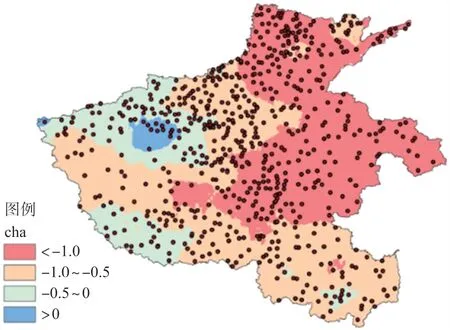
图9 次气象站点订正与模式风速绝对误差分布

总体特征:如表1 所示，从所有优选站30 天72 个预报结果总体均值来看，订正均值与观测均值非常接近，偏差仅为0.1 m/s～0.3 m/s；而模式预报均值偏差达到1.4 m/s～1.8 m/s。从绝对误差来看，模式的绝对误差为1.8 m/s，订正后绝对误差为0.9 m/s，92%优质站67.2%的时次都有改进。从675 个优质站推广到2 298个格点，与675 个优质站的统计结果非常接近。

次气象站点风速依据地理分布特征如图8 和图9 所示，从订正效果的绝对误差来看，中东部平原地区的误差小，西部山地误差大；和模式的绝对误差相比，订正后绝对差减小幅度最大的是北部和中东部，绝对误差减小1.0 m/s 以上；西部山地减小幅度不大，绝对误差减小不到0.5 m/s，部分地区订正后绝对误差比模式误差还大。次气象站点风速均值如图10 所示，模式与订正风速与观测风速的日变化特征基本一致，白天风速大，夜间风速小。订正误差在第二天中午前后最大，其他时间比较平稳。

图10 次气象站点风速均值统计结果

为了验证资料同化的作用，该部分工作主要将INCA 预报产品和同期的输入INCA 的区域模式场资料与某省境内119 个国家气象站常规观测资料进行相同参数的统计对比分析，检验资料同化对地面要素预报性能的影响。

各要素预报平均绝对误差曲线如图11 所示:从分析时刻到12 h 预报时效，气温、湿度、风速、风向预报误差缓慢增长，各要素的INCA 系统预报绝对误差增长情况为:温度从0.3°增加到1.5°，相对湿度误差从3%增加到10%，风速从0.3 m/s 增加到1.8 m/s，风向从30°增加到50°，这种预测准确率的水平与INCA 在奥地利的应用水平相当，各要素INCA 预报的效果均优于数值预报结果。

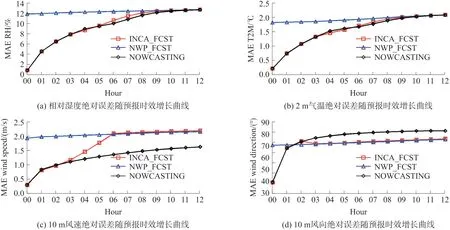
图11 INCA 系统在某省预报区预报效果检验

通过上述统计检验及分析可知，应用INCA 系统同化融合了某省区域几千个区域站资料及14 部雷达资料后，常规要素(温度、风速、风向、湿度等)和降水的预报效果均得到了改善，在12 h 预报时效内，均是INCA 的效果比INCA 接入的背景场BJRUC效果优。

4 结论

本文基于准确的气象要素预报提出了基于数值分析的电网精细化气象数值分析技术，通过研究得出以下结论。

①数值分析预处理以实时资料融合及外推预报系统INCA 开展某省区域地面观测资料在数值预报产品中的融合同化及预报技术研究，在0～6 h 内的多要素预测结果都是外推结果，而6 h～12 h 之间是外推预报和数值预报的融合结果，

②降尺度预报采用微尺度模式来进行，利用质量守恒原理对风场进行动力诊断，采用三维无辐散处理消除插值产生的虚假波动，生成重点区域水平分辨率为1 km 的未来三天逐小时预报结果，预报要素包括气温、风速、风向、气压、湿度和降水等，预报高度层为地面、30 m、50 m 和70 m。

③订正模型引入实时预报误差作为订正因子，针对地面要素建立精细化的客观订正预报模型，通过订正模型前后对比效果验证，订正模型提高面向电网的气象要素预报精度。