惯性MEMS 传感器在输电线舞动状态监测中的优化设计与应用∗

丁 杨，林孟豪，路金达

(国网新疆电力有限公司电力科学研究院，新疆 乌鲁木齐 830000)

我国能源分布广阔、负荷中心距离能源中心远，需要大量长距离的输电线路来完成能源供给[1]。由于地理位置原因，我国是遭受输电舞动灾害最严重的国家。输电线路舞动会严重影响输电质量，产生线路跳闸、金具磨损等问题，严重时甚至会使得线路断裂、电塔倒塌，出现输电停运等事故[2]。通过技术手段进行舞动防御，虽然可以处理相关问题，但是投资成本巨大，不具备全面操作性。

输电线舞动的原因是由于气流的作用，当受到风速影响或者输电线覆冰时，舞动概率大大增加。对于输电线的舞动幅度进行监测和抑制，对于输电线路安全具有重要的意义[3]。惯性微机电系统(Micro-Electro-Mechanical System，MEMS)传感器由于成本低、使用方便、不受天气影响、更智能的优点，被大量应用于输电线舞动状态监测之中[4]。李国倡等[5]研究了MEMS 惯性传感器的积分发散问题，利用位移频域积分方法，提高了传感器位移还原的精度。Shao 等[6]研究了一种新的陀螺加速度计，通过磁力计等的添加，使得线路舞动信息的监测更为精确。但是，当前的舞动监测系统采用的加速度传感器多为三轴加速度计，使得在监测过程中无法有效反映线路扭转和相对位移情况。

本文研究了基于六轴传感器的舞动监测方法，通过仿真和验证，证明其相比三轴MEMS 传感器具有更好的精度，并利用相关算法，实现输电线的姿态还原，且还原精度更高。

1 输电线舞动状态监测

1.1 输电线舞动

输电线舞动的方向通常垂直于导线的轴向，摆动过程中伴随一定程度的扭转。一般情况下，摆动和扭转是同时存在的，两种运动频率相近[7]。从表现程度上来说，扭转和摆动只有一个运动表现剧烈，另一个表现的并不明显。

气流的运动引起输电线的小幅摆动，对于输电线路来说影响并不明显。线路舞动具有持续时间长、摆动幅度大的特点，从而会严重加剧线路和输电塔的负载，尤其是在降雪、冻雨、覆冰等恶劣天气时，线路舞动的破坏力十分巨大，需要对其加以监测和抑制，避免电力输送被破坏。

当受到轻量风荷载时，输电线路会发生横向摆动，忽略其他条件因素时，输电线摆动的线速度Ul可以近似为风速U。而恶劣情况下的输电线，不再是圆形，从而在受到风速作用时，存在一部分力的分量，使得线路垂直运动。因此，当线路受到剧烈荷载时，线路的舞动属于两个自由度的运动，在垂直方向上同样会有剧烈的运动存在。

1.2 舞动参数

对于输电线路监测来说，其系统测量的参数主要是舞动的速度、加速度、角速度等参考量[8]。但是对于线路安全性来说，其关键参数主要包括舞动幅度大小和舞动的频率。

输电线路允许其幅度在一定范围内摆动，通常情况下舞动时的幅值大约为输电线直径的5 倍～300 倍，从而使得输电塔与线缆的连接受到巨大应力作用，舞动幅值越大，线缆断裂的概率越高，从而需要在舞动状态监测时，密切注意其幅度大小。

除了舞动幅度，另一个影响线路受力的因素为舞动频率，不同的频率作用下，线路受到的力并不一致，一般情况下共振时线路受到的应力最大。线路舞动的频率介于0.1 Hz～3 Hz 之间，会严重影响线路的安全性，因此需要在监测过程中，利用幅值对线路舞动频率加以监测。

根据国家电网的企业标准文件，«输电线路舞动监测装置技术规范»要求，输电线路的监测中，对于线路舞动的技术参数要求其舞动误差低于10%。

从而需要利用高精度的舞动监测系统来完成状态监测任务。

1.3 惯性MEMS 传感器

MEMS 是一种新型的加工技术，利用微电子的工艺加工出一系列机械装置结构[9]。由于尺寸小、结构稳定、性能好，被广泛应用于各传感器的制备和设计之中。

惯性MEMS 传感器主要包括加速度计、陀螺仪等常用惯性器件，利用传感器微结构之间的电参数变化，通过公式换算后，得到一系列惯性参数。惯性MEMS 传感器可以等效为一个“质量块－弹簧－阻尼”系统，用于其力学分析。

利用MEMS 传感器进行舞动测量，属于一种接触式的监测方法，通过将传感器与输电线固定，从而利用传感器的惯性信息来表征输电线的舞动状态参量[10]。利用MEMS 传感器的机理，可以用来记录输电线上监测位置处的加速度，并可以通过积分，获得输电线的位移情况。

假设输电线的某点，在t时刻的加速度为a(t)，则其速度可以由加速度进行求解，用公式表示为:

由速度方程可以获得t时刻位移s(t)，表示式为:

式中:v0为输电线在0 时刻的初速度，s0为0 时刻时输电线的初始位置。式(1)和式(2)中均包括X、Y、Z三个轴向的位移速度参数。

对惯性传感器来时，其收集的数据均为离散数据，从而需要将加速度和位移进行离散化求解。设定传感器的采样时间间隔为Δt，则离散形式的加速度和位移方程可以表示为:

2 舞动参数识别算法

利用惯性MEMS 传感器对输电线的舞动状态进检测，需要检测舞动的各种参数，包括角速度、加速度、幅度、频率等，需要利用一定算法对其进行求解。

2.1 识别流程

根据惯性导航的基础参数求解理论，可以利用惯性导航系统中的参数输出，获得陀螺仪的角速度输出值[11]。并可以在确定陀螺仪初始角的情况下，根据角速度的大小，求得输电线的空间姿态。

由于加速度的空间坐标系，分别对应X、Y、Z三个轴向，而惯性导航系统的求解需要在统计坐标下完成，因此需要利用姿态转换矩阵，利用不同坐标系下加速度进行坐标系转换，使其统一至导航坐标系坐标，进而求解目标空间姿态角度、速度和位移等参数。

识别算法的过程主要在于，将线路的舞动参数进行辨别，尤其是输电线的舞动幅度、舞动频率等。

识别的过程主要包括:检测传感器以及线路的空间姿态，对加速度坐标进行统一转换，并将由于重力引起的加速度分量进行删减。优化后的加速度可以根据积分计算，求得线路舞动幅度、频率等关键参数。

特征参数的识别，主要利用模块思路进行处理，将传感器数据通过预处理、姿态计算、参数求解三个过程，完成整个数据处理过程。

利用数据预处理，将器件的零漂、误差干扰项进行处理，以提高数据的有效性和准确性[12]。姿态计算求解获得输电线的空间姿态，进而可以通过处理后的加速度数据对舞动参数利用积分算法进行求解。

2.2 空间姿态求解

空间姿态的求解是对于输电线舞动参数计算的关键步骤，精确的舞动姿态求解，可以有效提高舞动参数求解的精度，是特征参数辨识的基础。

根据三轴加速度计和三轴陀螺仪均能获得其姿态角[13]。但是加速度计获得姿态角会受到输电线的高频信号干扰，使得航向角结果出现误差。而陀螺仪的姿态角容易受到零点偏移的影响和外界干扰的作用，从而形成累积误差。因此需要通过算法来将其进行融合，以获得准确的姿态角。

利用Mahony 滤波融合可以有效处理上述问题，结合两种传感器的姿态角，获得精确的计算结果。其滤波融合的原理图如图1 所示。

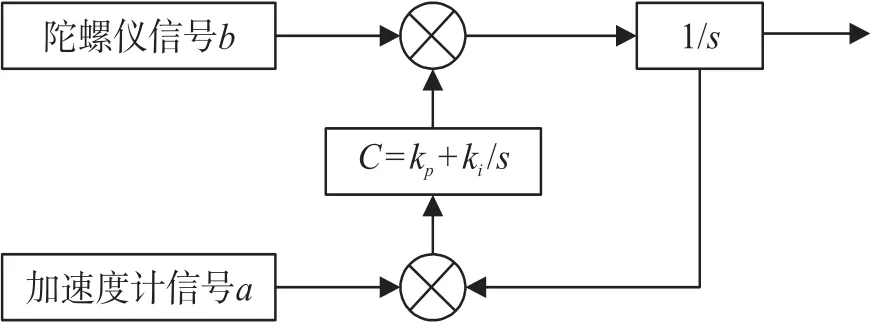
图1 Mahony 滤波原理

Mahony 滤波的姿态预测要求系统处于平衡状态，存在运动加速度情况时，会导致补偿和修正后数值不准确情况。因此需要对其进行修正，以使其适应输电线舞动监测的工作环境。

传统Mahony 滤波的两个重要参数kp和ki是固定数值，需要进行修正以适应加速度的显著状态。根据系统工作状态对参数进行优化，优化结果为:

2.3 舞动幅值辨识

在统一的坐标系情况下，需要对输电线舞动的加速度中减去由于重力加速度引起的变化。进而可以获得惯性系统的方程:

式中:f为MEMS 加速度计的输出加速度，Cn为惯性系统的姿态转化矩阵，g为重力加速度。

对舞动加速度进行二次积分，即可获得线路的舞动幅值[14]。由于单纯时域或频域积分均会给系统带来不小的积累误差，因此可以采用时域频域混合的积分方式。

具体计算过程为:利用时域积分去除数据中的一次误差，利用频域二次积分，获得精确的舞动幅值。

输电线路舞动速度的计算公式，如式(3)所示。对于式中N比较大的情况，会增加系统数据的计算量，占用大量的系统资源。因此可以将式(3)利用迭代计算的方式进行表示，公式为:

将式(8)中的离散速度，在频域下积分，以便获得输电线的舞动幅度。

对于时域速度信号v(NΔt)，其中共存在N个速度数据，每个数据的时间间隔为Δt，假设数据的分辨率为Δf，则傅里叶变换后的频域离散速度可以表示为:

将频域速度进行积分，即可获得傅里叶变换后的频域位移S(k)，利用傅里叶积分变换关系，可以得到:

式中:ωk为位移变化的频率，H(k)为模型中对应的数字滤波器输出，其表示式为:

式中:fd为速度频域信号的下限截止频率，fH为速度频域信号的上限截止频率。

将式(10)中的S(k)进行傅里叶逆变换，从而可以获得位移的时域信号S(nΔt)，获得输电线路舞动的幅值。

2.4 舞动频率辨识

输电线的舞动状态类似于两端固定的圆周运动，从而使得线上某点的运动轨迹为水平运动、垂直运动或者圆周运动情况[15]。由于端点固定，不同位置上传感器的舞动幅度并不相同，但是在相同的时间里，舞动的周期是一致的，从而也具有相同的舞动频率。

根据舞动幅度的周期性变化情况，获得在采样时间T内的舞动频率f，用公式表示为:

式中:N为T时间内，幅值变化的周期数量。

3 实验结果与数据分析

为了验证本文关于惯性MEMS 传感器在输电线舞动状态监测方面的准确性，在实验室中对本文算法进行验证。

由于输电线的舞动类似于圆周的特性，因此实验平台的搭建采用卓立汉光的单轴转台和悬臂进行舞动模式模拟，转台具有高的定位精度，角度定位优于0.01°，转速可以达到60 °/s。选择六轴惯性传感器为InvenSense MPU－6050。

3.1 姿态求解测试

对于传感器的姿态求解算法采用本文的改进Mahony 滤波算法。将MEMS 惯性传感器固定于转台转接板处，分别考虑不同航向角、不同俯仰角和不同横滚角情况下的测试情况。

不同姿态情况下的求解测试结果如表1 所示。

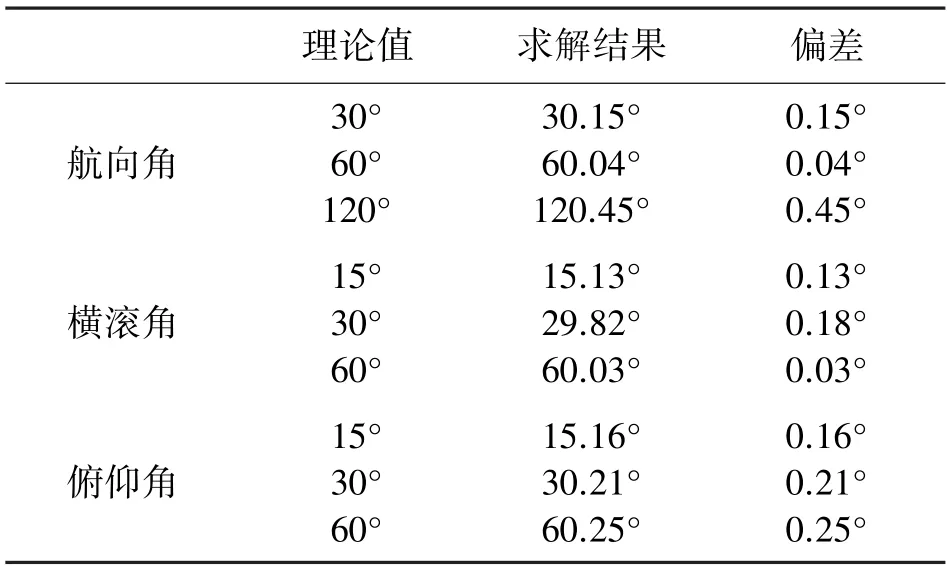
表1 姿态求解结果

从表1 的结果可以看到，对于航向角的求解结果，其偏差低于0.45°，横滚角及俯仰角的偏差也很小，均低于0.25°。通过算法修正，利用姿态转换矩阵和重力加速度去除，使得角度的偏差可以进一步降低。对于输电线路舞动状态的参数总偏差低于10－3，符合电力系统对于输电线路舞动偏差的精度要求。

利用转台特性对40°测试俯仰角进行周期为T的周期性变化，比较改进Mahony 滤波姿态算法与传统Mahony 滤波算法之间的准确性情况。两种算法的结果如图2 所示。

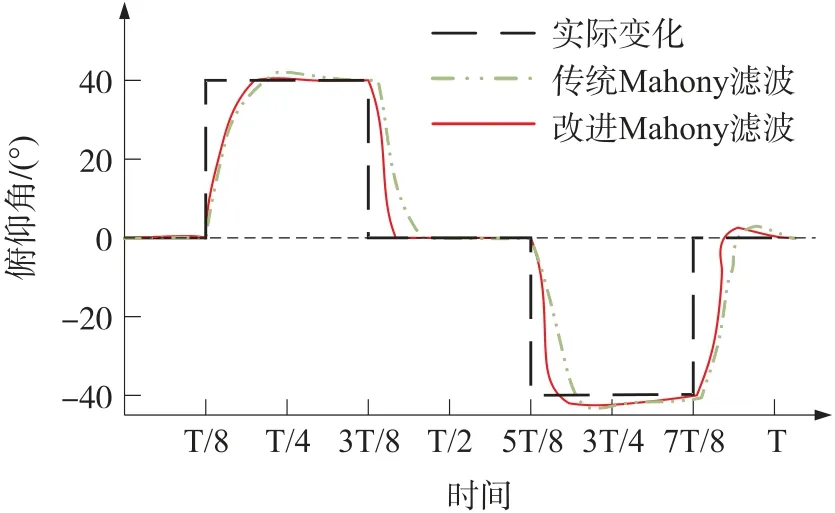
图2 算法对比

从图2 中可知，两个Mahony 滤波姿态算法都可以很好地对系统姿态进行估计，但改进Mahony 滤波姿态算法对于转动姿态的跟踪更为精确，姿态变化更迅速，产生的误差更小。

3.2 舞动特征参数辨识

①静态特征辨识

在角度为45°的静态倾斜块上，固定本文的惯性MEMS 传感器，分别调节其俯仰角、横滚角，设定角度为30°和－30°的情况下，计算其加速度情况，结果如表2 所示。

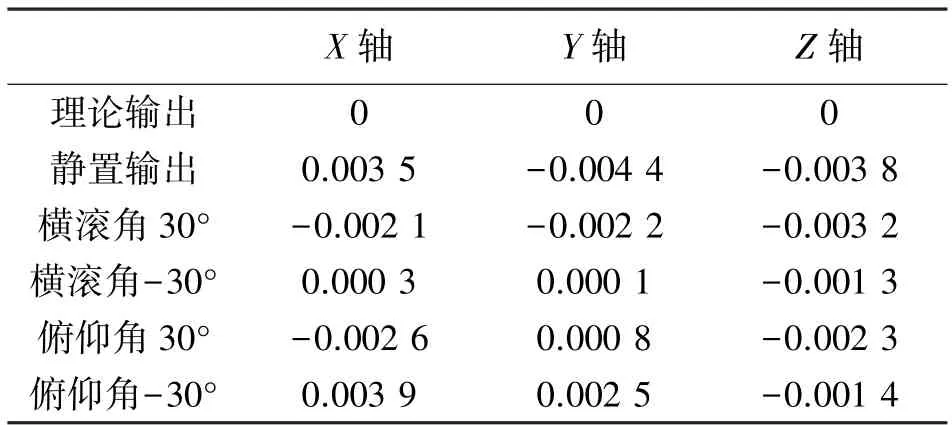
表2 运动加速度对比 单位:m/s2

从表2 的结果上可以看到，在静态的情况下，传感器输出的加速度误差大小均低于0.005 m/s2，与理论结果具有良好的吻合度，证明本文算法的有效性。

在不同的俯仰角和滚动角情况下，加速度的误差更低，低于0.004 m/s2，与理论结果的符合性更好，为运动模式下的加速度求解奠定基础。

②往返动态特征辨识

设定水平滑台进行往返运动，在固定频率下，计算传感器在线性运动状态下的特征参数，结果如表3所示。

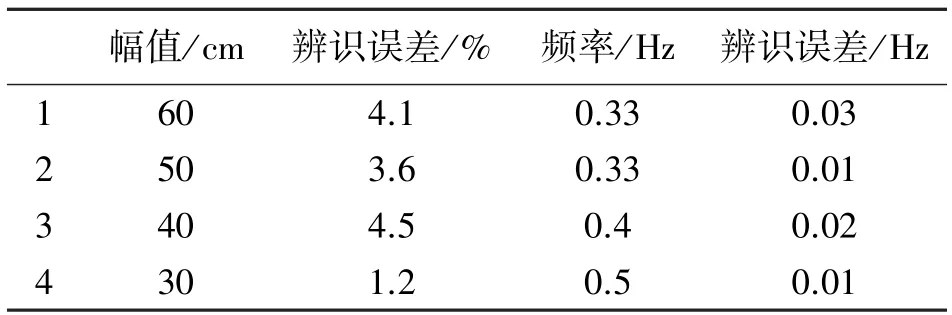
表3 不同往返运动参数辨识结果

从表3 的结果可以看到，本文状态辨识结果与真实数据十分接近，其中幅值辨识误差的最大结果为4.5%，而频率的辨识与实际情况十分接近，最大误差约为0.03 Hz，证明本文算法在往返运动中的精确性和合理性。

③转动特征辨识

将六轴惯性MEMS 传感器固定于转台连接板处，使转台进行周期匀速旋转，设定悬臂长度为50 cm，转动频率为0.1 Hz。

利用本文算法监测测试平台的转动参数和特征参数。对转动平台的幅值进行辨识，辨识结果如图3所示。

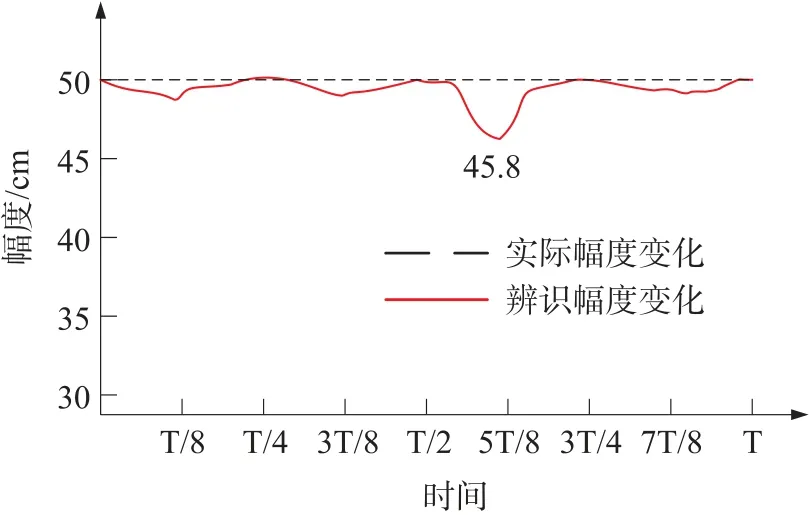
图3 幅值辨识结果

从图3 的幅值辨识结果可以看到，本文辨识算法的误差很低，幅值偏差低于4.2 cm，平均误差低于1.5 cm，相对误差约为3%，符合输电线舞动的测试要求。

对幅值进行傅里叶变换，利用识别算法求得传感器的运动频率，计算结果为0.105 Hz，与实际结果相近。

对上述转动运动在不同条件下进行多次测试，平均测试结果如表4 所示。

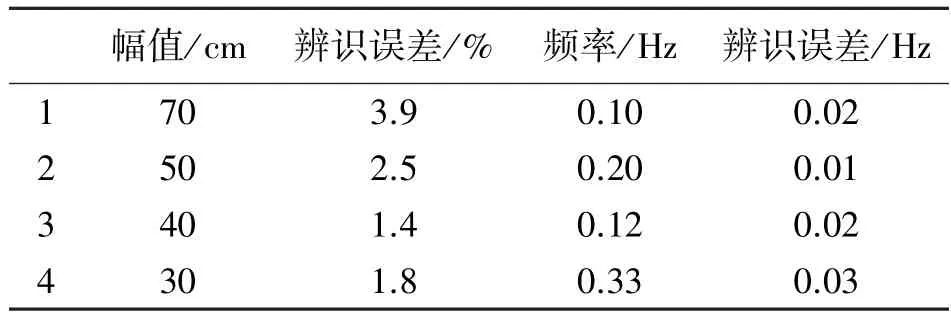
表4 不同转动运动参数辨识结果

从表4 结果可以看到，本文辨识结果在转动幅度方面误差低于4%，最大辨识误差出现在幅度为70 cm情况下。在频率辨识方面，辨识结果与实际频率接近，最大误差为0.03 Hz，出现在转动幅度30 cm情况下。

从辨识结果可以看到，本文辨识的幅度和频率均与实际运动结果一致，证明本文算法在舞动特征参数获取方面的准确性。

4 结论

对于惯性MEMS 传感器在输电线舞动状态的监测问题，本文主要研究了关于舞动状态的算法优化，利用改进的Mahony 滤波姿态算法，可以更好地对处于加速度状态下的输电线姿态进行辨识，利用时域频域结合的方式，使得对于舞动参数的计算更为精确。在实验条件下，对本文的研究内容进行验证，分别考虑稳定状态下、往返状态下以及转动状态下的辨识误差情况，从最终的结果来看，无论是舞动幅度还是舞动频率，辨识误差均很低，最大幅度误差约为4%，频率误差低于0.03 Hz，可以满足输电线舞动状态监测的需要。