基于灰狼算法的步进电机滑模控制系统设计

白天羽,赵南南,马毓敏,宗世祥

(西安建筑科技大学机电工程学院,西安 710055)

0 前言

随着我国现代化工业的发展,转台作为机电一体化控制的集合体,已经被广泛应用于模拟飞行器运动系统、雷达通信系统、航空航天技术等重要领域。

步进电机作为数控伺服电机,具有定位精度高、响应速度快、无累积误差等优势,在转台控制系统中应用广泛,学者们对此展开了深入研究。Son 等[1]在有界扰动、不确定性的情况下,对步进电机位置控制系统展开了研究,提出了一种自适应增益超扭曲滑模观测器,使用动力学方程进行了证明,实验验证了该算法的位置估计性能得到了提升。文献[2]使用绝对式光栅记录了位置误差,设计了模糊PID 控制系统,实验证明设计系统在一定程度上削减了抖振现象,提高了控制系统的位置精准度。文献[3]对步进转台建模,测试控制系统输出脉冲信号的幅值增益与相位偏移量,应用抽象粒子群-遗传算法迭代计算,得到建模控制的待定参数,实验结果表明设计的控制器精准度较高。文献[4]将时变边界层滑模算法应用于步进电机控制系统,实验验证了控制系统具有较高的位置精准度,削弱了抖振现象。Li 等[5]为了解决控制系统存在的非线性因素影响,通过功率近似法提出了新的滑模趋近律算法,使用李雅普诺夫理论证明了控制器的稳定性,仿真验证了该控制系统的响应速度较快、抗干扰能力较强。Zhao 等[6]提出一种步进转台闭环控制系统,系统使用BP 神经网络算法优化了双轴转台控制系统的PID 参数,实验验证了优化后的控制系统具有较高的跟踪精度。Chen 等[7]为了降低转台低速工况下的摩擦现象,使用指数收敛性的扰动观测器设计滑模控制器。通过与PID 控制系统进行比较,优化后的控制器克服了低速时的摩擦力,具有较高的位置精准度。文献[8]设计了频域控制与滑模控制系统结合的双闭环控制器,通过伺服转台硬件平台验证了设计的双闭环控制系统具有较强的抗干扰能力。文献[9]将反步法、自适应滑模和LuGre 模型应用于光电转台控制系统,引入积分滑模切换面降低了稳态误差。通过实验证实该方法有效弥补了摩擦产生的误差,提高了系统的循迹精度。

本文选择步进电机作为控制载体,设计了一种灰狼算法与滑模算法结合的位置闭环控制方法。通过灰狼算法搜寻滑模参数最优值,输入到滑模变结构控制的初始端。其中指数趋近律方程选择了积分滑模切换面,引入Sigmoid 函数,搭建了基于MATLAB/Simulink的位置三闭环控制系统仿真,对系统位置的动态性能、抗干扰能力进行分析与对比。最后搭建以STM32F10ZET6 为主控芯片的硬件平台验证系统的位置精准度与稳定性情况。

1 电机控制系统的数学模型

在忽略了涡流效应、定转子漏磁现象、磁滞的情况下,两相绕组的电压可表示为:

式中,UA、UB分别为A、B 两相绕组的端电压;iA、iB为A、B 两相绕组相电流;L0、L2分别为定子绕组的自感平均系数和自感基波系数;ω为转子实际角速度;rA、rB为两相内阻;θ为转子角度;ke为反电动势系数;t为电机运行时间。

步进电机机械运动方程可以表示为:

式中,Te为电磁转矩;J为转动惯量;B为粘滞摩擦系数;TL为负载转矩。

两相步进电机的矩角特性表示为单相励磁转矩的矢量和[10],电磁转矩可以表示为:

式中,Nr为齿数;Msr为定转子之间的互感系数;Im为励磁电流值。

在静止坐标系中,转子位置角随着电机运行而不断变化,为了简化步进电机的数学模型分析,本文引入了dq旋转坐标系。

电流id、iq在旋转坐标系下可表示为:

电流iA、iB在静止坐标系下可表示为:

旋转坐标系下的电磁转矩如式(6)所示,可联合式(3)～(5)求得:

当id=0 时,iq正比于电磁转矩,如式(7)所示:

2 位置控制方程设计

2.1 滑模控制原理

滑模变结构控制为一种非线性控制方法,非线性指控制的不连续性[11]。在一定的特殊规则下,通过不同的切换规律,迫使系统在状态轨迹上做小幅度运动,使系统符合所期望的点位。趋近模态运动是指在限定时间内,由任意初始位置沿着空间滑模表面的任意一点滑行的运动。如果系统在滑模面的切换过程不存在空间滞后与系统惯性的影响,系统的滑模运动将是光滑的,不存在抖振情况。现实应用中无法避免抖振情况的出现,在开关系统中产生抖振现象的原因是切换的滞后[12]。削弱抖振主要手段有两种:对理想切换采取连续近似的方法[13],优化趋近律的方法[14]。

为了减弱抖振现象,越来越多的学者通过设计出合理的控制方程,并结合其他控制策略使电机系统的位置精准度与稳定性得到有效的提升。文献[15]对三轴转台系统的位置精准度进行研究,采用扩展卡尔曼滤波算法辨识了各项坐标的惯量参数,对摩擦造成的误差进行了补偿,应用神经网络算法整定补偿方程的控制参数,实验验证了设计的控制系统的位置精准度较高。文献[16]采用天牛须算法整定了PID 控制系统的参数,将其与模糊PID 控制、传统PID 控制进行了比较,优化后的控制系统具有较小的稳态误差,响应速度较快。文献[17]为了提升永磁同步电机调速系统的响应速度,采用粒子群算法优化PI 模糊控制器的比例项与积分项系数,仿真验证了优化后的控制策略的鲁棒性较强,响应速度较快。

2.2 滑模控制器设计

选择指数趋近律可以改善滑动模态的品质,减弱控制系统的抖振情况。位置变化的中间变量如式(8)所示:

式中,e为位置误差值;θref为期望位移量;θreal为实际位移量。定义滑模切换面如式(9)所示:

式中,s为滑模面;kp为比例变量;ki为积分变量。求导可得式(10):

本文选择Sigmoid 函数代替传统的符号函数,该函数曲线是连续变换且光滑的图像,在自变量趋于无穷大时函数值无限趋于1。将两者结合作为步进转台的趋近律,如式(11)所示:

式中,ε为切换增益系数;k为设计参数;X为状态变量;α为状态变量的指数值,α＞1。

式中,a是大于零的任意数。s为滑模面,当s趋于正无穷时,因变量为1;当s趋于负无穷大时,因变量为-1。联立式(10)与式(11)并整理可得:

对位置误差求导可得角速度误差值,如公式(14)所示:

联立式(13)与式(14)可得位置控制的趋近律,令U=ωreal,可得:

式中,U为指数趋近律的控制率;k越大趋近滑模面的速度越快;切换增益系数ε越大收敛速度越快,接近滑动表面的速率快一些,不过存在明显的抖振现象;切换增益系数ε越小,抖振现象会在一定程度上削弱,但收敛速度又会变慢。通过调整合适的滑模参数值,尽可能增大设计参数,减小切换增益系数,不仅缩短了有效时间,还削弱了抖振现象。

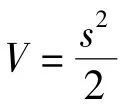
式中,ε＞0,α＞1,k＞0,即s·s·恒小于0,确保控制系统有较快的收敛速度并可以到达滑模切换面。

2.3 灰狼算法整定参数

在解决实际工程问题中,种群智能算法由于较容易实现,收敛性较强,在复杂的非线性问题上应用广泛。Mirjalili 等[18]提出了新的智能优化算法:灰狼算法(GWO)。在精确度和收敛速度上,灰狼智能算法大大提高了解决具体工程问题的能力。Madadi 等[19]使用灰狼算法整定PID 控制的参数,优化后的系统降低了稳态误差,提高了抗干扰能力。文献[20]对永磁同步电机系统的不确定因素对鲁棒性的影响,采用改进的灰狼算法优化了滑模控制器的参数。在空载与增加固定负载转矩的工况下,通过仿真对比了自抗扰控制系统与传统滑模自抗扰控制系统,实验结果验证了优化后的控制系统具有较强的鲁棒性。

灰狼种群的自适应过程包括搜寻猎物、包围猎物、攻击猎物。灰狼算法的结构较简单、需调参数少、实现较容易、全局域搜索能力强、收敛速度较快,适用于非线性控制系统。步进电机系统若采用传统的拼凑法整定控制方程参数,会存在一定的偶然性、较大的误差、耗时较长、控制效果不显著等问题。故本文选取灰狼算法对滑模控制系统的多项未知参数进行整定,将得到的最优数值输入到位置控制器中,图1 为GWO 优化滑模控制系统位置三闭环。

图1 GWO 优化滑模控制系统位置三闭环

关键在于灰狼算法自适应搜寻控制率未知变量Kp、Ki、α、ε、k的值。

灰狼种群分别表示为α狼、β狼、δ狼、ω狼,α为种群中的头狼,负责群体各项决策事务,如狩猎、休息时间与地点、食物分配等。β为种群的智慧团队,主要协助α执行决策,β的支配地位仅次于α,β将α的命令传达给种群中的其他个体,并将种群成员的执行结果反馈给α狼。δ听从于α、β的命令,主要负责侦查、放哨、看护等事务,ω主要维持种群内部的平衡关系[21-22]。灰狼种群包围猎物过程定义为:

剩余ω个体向最优三匹狼靠近的位置向量如式(21)所示:

ω狼的当前位置向量如式(22)所示:

当猎物被锁定时,灰狼种群展开攻击,收敛因子会不断的减小,随着时间由2 递减至0。

图2 灰狼种群搜寻猎物过程

使用灰狼算法寻优滑模位置控制器中的未知参数,选择MATLAB/Simulink 仿真软件中的workspace模块连接到M 编辑器,将未知参数Kp、Ki、α、ε、k的值输入为自变量,设定种群为100,迭代次数为100,实现自适应寻优。

图3 为灰狼算法优化参数流程图,首先初始化种群,其次比较个体间的适应度值,确定最优解、次优解、第三优解,更新收敛因子,系数向量和的值;然后更新最优三匹狼的位置与适应度,最后迭代次数未达到最大次数重复以上步骤,达到最大迭代次数输出优化后的各项滑模参数值。

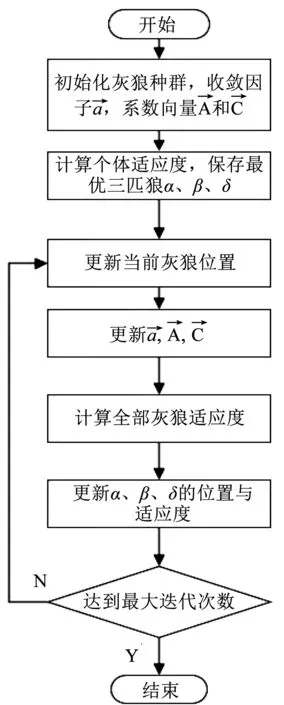
图3 灰狼智能算法流程图

图4 为自适应曲线对比图,使用灰狼算法分别寻优了PID 与指数趋近律的参数,由图中看出滑模控制系统的适应曲线收敛速度更快、效果较好,在一定程度上提升了指数系数、减少了切换增益系数。

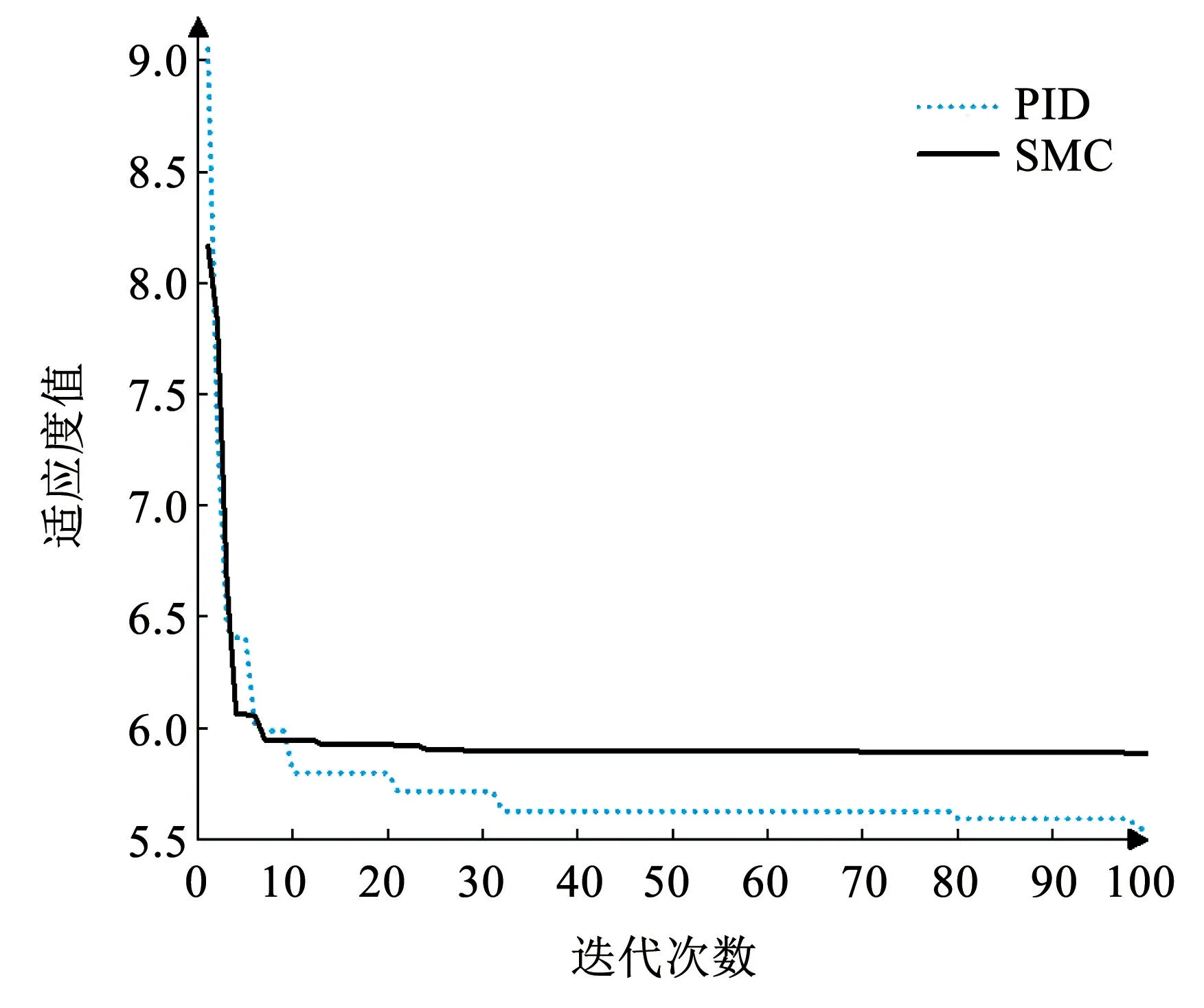
图4 自适应曲线对比图

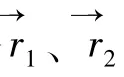
3 仿真验证

使用MATLAB/Simulink 验证灰狼算法优化后的滑模控制系统的性能,仿真模型如图5所示。灰狼算法对指数趋近律的多项未知参数进行自适应寻优,得到最佳数值输入到位置控制器中。速度闭环采用PI控制电机转速,比例系数为2.5698,积分系数为1.4596。电流环采用id=0 的控制方式,对两相电压进行Park 反变换,通过SVPWM 模块采样电压脉冲信号输入到步进电机。编码器将速度、电流值及位移及时反馈,经过Park 变换得到电流值进行反馈调节。

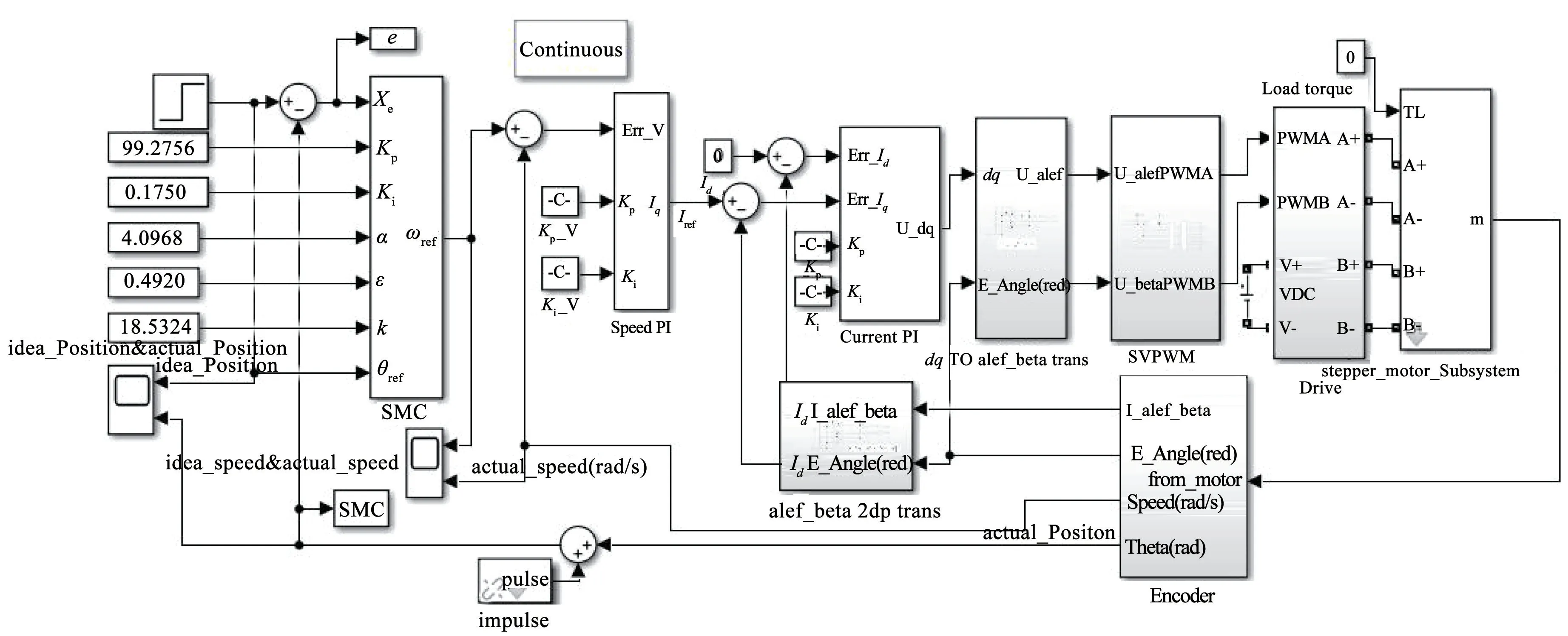
图5 基于GWO 优化滑模的位置控制MATLAB 仿真模型

图6 为控制系统的位移对比情况,由图中看出在参考位移量为1cm 时,PID 的位移在15ms 系统产生了超调,在75ms 达到参考位移值。传统滑模控制系统在75ms 达到参考值,但响应速度较慢。使用灰狼算法优化的滑模控制系统在15ms 很快达到期望位置值,且没有发生超调,位置的精准度得到改善。

图6 转台控制系统的位移量对比图

图7 为带干扰信号情况下的控制系统位移量对比,仿真在125ms 加入脉冲宽度为0.01 的干扰信号测试控制系统的鲁棒性。从图中可以看出GWO-SMC控制系统的响应速度快,没有产生超调。

图7 加扰动的控制系统比较图

图8 为加入扰动信号的局部放大图,由图像可观察到PID 控制系统的振幅较大,抖振现象较明显,抖振最低点为0.93688cm,在166ms 恢复到期望位移值。传统的滑模控制系统振荡较小,抖振最低点为0.96744cm,在163ms 恢复到期望位移值。灰狼算法优化后的滑模控制系统振荡最低点为0.97682cm,在145ms 恢复到了期望位移值,其抗干扰能力与前两者相比较强,控制效果较好。

图8 加扰动控制系统的位置局部放大图

4 实验验证

为了验证电机控制系统的可行性,选择STM32F10ZET6 为主控芯片搭建了硬件测试平台,该芯片具有高性能、低功耗、低成本的特性。在Keil μVision5软件中,使用C 语言编译PID 控制与优化后的滑模算法程序进行比较。

选用两相混合式步进电机,具体参数见表1。图9为步进转台控制系统的现场测试图。将上位机、核心控制板、电源、驱动器与步进电机依次连接。

表1 步进电机参数

图9 步进控制系统实验测试图

上位机界面通过Modbus 应用层协议将指令信号传送给串行链路上的RS485 通信,协议选择RTU 模式提高了串口传输效率,使用串口指令控制步进电机正常运转。

当步进电机控制系统的额定转速为600r/min 的低速工况下,实验使用PB632 型动平衡分析仪测试系统的性能,使用±0.01°的角度传感器检测步进电机控制系统的精准度。现选取120°与360°测试控制系统的位移角度。

步进电机控制系统在启动阶段会产生波动,实验过程统计了500～600ms 平稳工作运行时的转动角度值,图10所示为位置指令控制电机转动情况,在图(a)中,使用PID 控制的位移误差范围保持在±0.23°,灰狼算法优化后的滑模控制系统误差范围保持在±0.16°。图(b)中可以看出PID 控制系统的误差范围保持在±0.24°,优化后的滑模控制系统的误差范围保持在±0.16°。

图10 位置指令控制步进电机角度测试

图11 为动平衡分析仪测试系统运行时的振幅速度有效值情况,1.8mm/s 为小型电机振动速度有效值的最大限值,实验测试的振动速度有效值越低表示电机的控制性能越佳[23]。

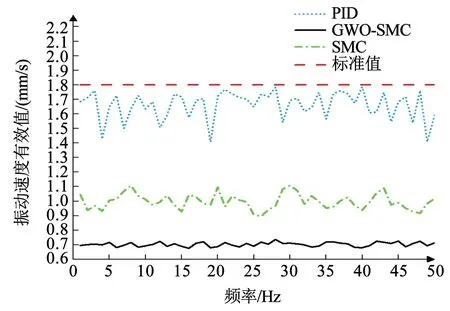
图11 步进电机振动速度测试图

当频率在50Hz 时,PID 控制系统振幅较高,数值波动范围较大,振动速度有效值在1.6mm/s 附近,抖振现象较明显。传统的滑模控制系统的抖振较小些,振动速度有效值维持在1.0mm/s 附近。灰狼算法优化后的滑模控制系统的振动速度有效值较低,数值波动范围较小,维持在0.7mm/s 附近,抖振现象得到改善,系统运行较稳定。电机的内部机械误差、放置表面的平整度、滑模控制系统的固有属性、步进电机的运行矩频特性是其存在小幅度抖振的主要原因。

5 结论

本文以提升转台控制系统的精准度与鲁棒性为目标展开了研究,针对步进电机位置控制系统进行设计。首先,选择了指数趋近律作为控制方程,应用灰狼算法整定滑模控制系统方程的多项参数。其次,通过MATLAB/Simulink 搭建了三闭环位置控制系统仿真模型,比较了PID 控制、传统滑模变结构控制的位移、抗干扰能力。仿真结果表明优化后的滑模控制系统对位置的响应速度快,位置精准度得到了明显的改善;在125mm 加入干扰脉冲信号时,控制系统的鲁棒性得到了加强。最后在低速工况下,通过实验证明了优化后的滑模控制系统的位移角度较PID 控制系统更精准,达到±0.16°,电机控制系统削弱了抖振现象,提升了鲁棒性,具有一定的工程参考价值与应用前景,后续考虑通过改进灰狼算法的搜索机制来提升搜寻精度与收敛性。