边缘计算网络中区块链赋能的异步联邦学习算法

黄晓舸 邓雪松 陈前斌 张 杰

(重庆邮电大学通信与信息工程学院 重庆 400065)

1 引言

据GSMA预测，2025 年全球物联网设备将达250 亿台，海量数据处理请求成为亟待解决的问题[1]。机器学习(Machine Learning, ML)可从用户环境等多样特征中挖掘出复杂的“模式和见解”[2]。ML的复杂计算推动了边缘计算网络(Edge Computing Network, ECN)的发展，为减轻云端负荷并减少任务反馈延迟，将任务卸载到边缘节点 (Edge Nodes, ENs) 计算[3]。此外，用户对隐私保护的关注日益提升，使得数据本地化处理成为当前热门研究方向[4]。

联邦学习 (Federated Learning, FL)允许多个设备在保证用户隐私的前提下共享模型参数[5]，由此受到多方关注，其性能优化方案层出不穷。文献[6]引入信誉机制，根据时间序列来预测信誉值，筛选高质量节点参与FL任务，提升训练性能。文献[7]提出一种异步聚合FL方式，可在收到模型更新后可立即聚合，无需等待所有节点完成本地训练，提高训练效率。但是，设备上传模型的时间和质量不确定，异步FL性能不稳定。为克服性能回退，文献[8]提出一种半异步FL，可自适应调整本地迭代数以解决掉队者问题。考虑到异步FL的复杂性，一些学者在网络结构上寻求突破。文献[9]发现神经网络深层参数的更新频率需求低于浅层，基于此特性，提出了时间加权的异步FL，使用不同频率更新深浅层模型参数，以减少数据传输量并提高学习效率。

传统FL的服务器容易遭到单点攻击，其数据安全面临巨大挑战。区块链技术包含分布式存储、共识机制等[10]，可有效提高FL的安全性。文献[11]旨在去除传统FL的中央服务器，提出由本地链和全局链构成的双层区块链。本地链按时间顺序记录本地模型，形成本地设备的长期信誉值。全局链被划分为逻辑隔离的FL任务链，以提高效率和可信性。文献[12]使用区块链记录FL中的高质量节点，使用三重主观逻辑模型计算节点的信誉值，作为节点筛选指标。此外，设计了一种质量证明机制，提高区块链共识效率。文献[13]提出了一个基于区块链的异步FL框架，使用动态比例因子提升FL训练效率，并保证训练的有效性。同时，提出基于委员会的共识机制，以尽可能小的时间成本保证可靠性。

为提高FL的训练效率与安全性，本文提出基于区块链的异步联邦学习(Asynchronous Federated Learning based on Blockchain, AFLChain)算法。本文主要贡献如下：

首先， AFLChain将网络中的任务发布者和响应者定义为主节点 (Primary Node, PN) 和次节点(Secondary Nodes, SNs)。为提高FL训练效率，SNs根据算力进行不同轮次的本地训练。PN持续本地训练至全局聚合，与SN构成异步FL。

其次，为解决FL中央服务器易受单点攻击的问题，使用区块链技术保证数据安全。区块链由PN和SNs领导者交替上传的两种区块组成，确保数据可追溯性。SNs领导者由熵权信誉机制选出。

此外，本文提出一种基于次梯度的最优资源分配(Subgradient based Optimal Resource Allocation, SORA)算法，通过联合优化计算和通信资源提升AFLChain的性能，最小化网络总延迟。

最后，广泛的仿真验证了所提算法的有效性。

2 系统建模及分析

2.1 系统模型

如图1，本文在ECN中实现FL架构，EN(如智能车间、智能楼宇等)具有足够的本地数据和算力，可支撑训练任务和共识算法。发布任务的EN为主节点(Primary Node, PN)，参与任务的 EN 为辅助节点(Secondary Nodes, SNs)。PN为可信节点，负责模型聚合，SN负责本地模型训练及上传。

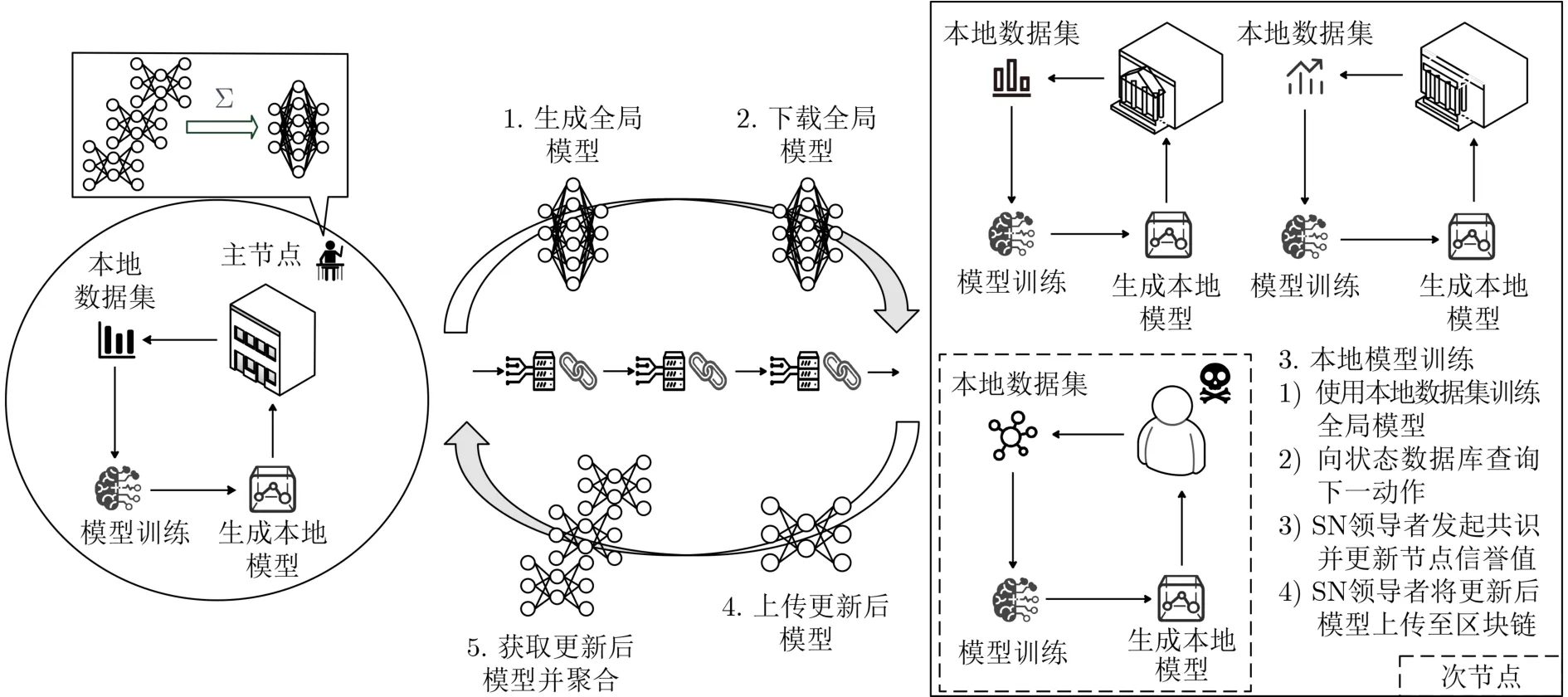
图1 网络结构图

在区块链网络中，所有节点共同维护一条联盟区块链，由PN和SN领导者交替上传的区块组成。共识机制也可用权益证明(Proof-of-Stake, PoS)等，但需要额外方案防止分叉。考虑到联盟链中节点较少，基于投票机制的实用拜占庭容错(Practical Byzantine Fault Tolerance, PBFT)机制更高效。

2.2 工作流程

设AFLChain中有1个PN和K个SNs。图2显示了一个epoch的工作流程，包含以下步骤：

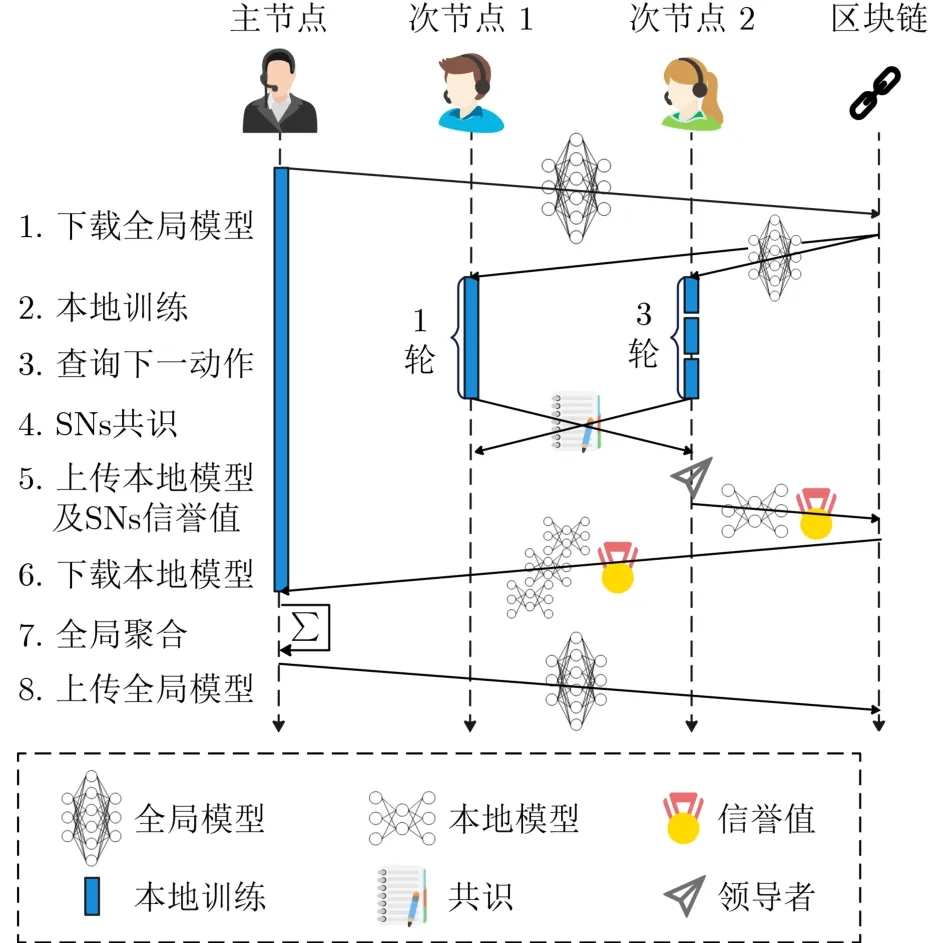
图2 一个epoch的工作流程

步骤1 SNs从区块链网络中获取全局模型。

步骤2 在epochh，第i轮本地迭代中，SNk使用本地数据集(Xk,Yk)的部分样本计算交叉损失熵作为损失函数，以获取模型梯度：

其中，b表示数据集样本大小，θ表示数据类别号，(X,Y)分别是数据的样本特征和标签。Fθ是模型权重ω的函数，表示输出为类别θ的概率。

本文采用随机梯度下降(Stochastic Gradient Desc ent, SGD)优化算法更新本地模型：

其中，η表示本地学习率。

步骤3 SN发送状态信息到状态数据库，查询下一个动作。如果返回操作是TRAIN，则继续进行下一轮本地训练，否则进入共识过程。

步骤4 所有SNs进入共识后， SNs领导者开启共识。共识达成后，SNk基于模型更新，本地训练轮数以及历史信誉值更新信誉值。

步骤5 SN领导者将SNs的信誉值与模型打包成块并上传至区块链。仅SNs领导者有权上传区块，所以分叉现象将不会发生。

步骤6 智能合约(Smart Contract, SC)通知PN从区块链下载更新后的SNs模型和信誉值。

步骤7 当PN接收到聚合信号，它将基于PN和SNs模型，采用加权平均策略进行全局聚合。

步骤8 PN将全局模型上传至区块链网络。

重复上述步骤至模型收敛或目标精度达成。

2.3 信誉机制

AFLChain依赖于多个SNs的共同维护，为保障模型质量，需对SNs进行评估。与主观加权方法相比，根据信息差异确定权重的熵权法具有更好的客观性。本文中，信誉值由模型训练进度、本地训练轮数和历史信誉值决定。信誉值大于上分位点thupper的SN为候选SN，信誉值最高的候选SN为领导者。信誉值小于下分位点thlow的SN为潜在SN，不能参与当前FL任务，其余为普通SN。本文使用余弦相似度表示模型间差异，以保证高维向量计算的准确性[14]。epochh中SNk模型与epochh-1中全局模型ωh-1的余弦相似度为

对于SNk,表示epochh中指标j的标准化值，均采用正标准化，其占比为

其中，j=1,2,3分别表示SNk在epochh-1的信誉值，本地训练轮数rk和余弦相似度sim(ωkh,ωh)。

指标j的熵权值为

3 异步联邦学习架构

为缓解同步FL训练效率低下的问题，本文提出异步FL算法，如图3，通过包含SNs状态信息的状态数据库调整SNs本地训练轮数，提高训练效率，其功能可在SC中实现以克服安全问题。

SNk状态信息为为epoch计数，rk为本地训练轮数，为本地训练时间，为查询时间，Tk为发信时间戳。

最后，由式(10)确认SNk是否进行继续训练，

其中，tc是状态服务器的当前时间戳。

SNk的等待时间可表示为

其中，Tqry为查询时间，相对于其他时延可忽略不计，则=0。为优化本地训练轮数rk以最小化整体等待时间，建立优化目标如下：

若式(10)成立，状态数据库返回ak=1。否则，剩余等待时间不够完成一轮训练，SNs领导者开启共识。flag为SC发送至PN的信号，flag=1表示聚合，否则PN持续训练。细节如算法1所述。

4 问题建模

4.1 计算模型

SNk的本地训练时间表示为

其中，ck表示SNk训练一个样本所需CPU周期，D为样本个数，表示SNk可提供CPU频率。

算法1 状态数据库决策流程

SNk训练模型所需的CPU周期数表示为ckD。因此，SNk在一次训练迭代中的能耗为

其中，β是SNk计算芯片组的有效电容系数。

4.2 通信模型

本场景中通信时延为共识和领导者块上传的时延。其中，共识过程分为块传播和块验证。

在块传播阶段， SNs向领导者l发送包含本地模型的块信息，传输速率(bit/s)可由式(17)计算：

其中，B表示带宽，pk为SNk的传输功率，gk,l为SNk到领导者l的信道增益，n0为噪声功率。

因此，在共识过程中块传播时延可表示为

其中，δb表示块大小。

在块验证中，SN确认块信息，确认时延为

其中，φb表示验证块所需的CPU周期数，为SNk验证块的计算频率。

此外，领导者l的块上传时延可由式(20)计算：

其中，γl为领导者l的传输速率，块上传能耗为

4.3 优化问题

为使SNs的本地训练时延、共识时延和块上传时延之和最小化，将优化问题建模为

其中， C1为SNk计算资源约束； C2表示块验证时延不能超过最大可容忍延迟； C3 和 C4表示模型更新和块上传的能耗限制； C5为传输功率约束。

4.4 资源分配优化

本节提出SORA算法解决优化问题(22)，首先根据 C4，最优块上传功率可表示为

(1) 最优计算资源分配

将pk视为常数并去除常量项，原问题简化为

为降低复杂度，采用交替求解法获取最优解。

其中，π1,π2是C1,C3的拉格朗日乘子。由Karush Kuhn Tucker (KKT)条件，可得以下充要条件：

为求解3次方程式(30)，引入盛金公式[15]。对3次方程ax3+cx2+cx+d=0，定义以下辅助变量：

结合式(30)与式(31)，可得如下判别式：

由盛金公式可知，当Δ=0时，该3次方程有3个实根，且其中两个实根相等。令Δ=0，可得

则等式(30)的3个实根表示为

π1和π2由拉格朗日对偶法求解，对偶函数为

因此，等式(25)的对偶问题可表示为

次梯度法可求解 (38)， π1和 π2的更新方程为

其中，t是迭代因子，ϵ1和ϵ2分别是更新步长。

(2) 最优传输资源分配

P2是单调递减函数，在传输功率最大的情况下达到最小值，从而有

算法2给出了SORA算法的细节，设定容忍阈值ϵ3，问题式(38)的复杂度为O(log2(1/ϵ3))，K个SN的复杂度表示为O(Klog2(1/ϵ3))，在迭代因子上限tmax下，SORA算法的复杂度为O(Ktmaxlog2(1/ϵ3))。

5 仿真结果及分析

5.1 仿真场景及参数设置

本文使用Python和Pytorch评估AFLChain的性能，Matlab验证SORA的有效性，采用Mnist和FashionMnist训练卷积神经网络(Convolutional Neural Network, CNN)，Cifar10训练ResNet18。路径损耗模型采用3GPP，140.7+36.7lg(ς)，ς为节点距离。默认算力比ρ=3，其他设置见表1。

表1 仿真参数设置

5.2 结果分析

图4展示了不同FL算法的性能。使用Mnist训练CNN，选取5个SNs参与任务。基线为单机训练CNN，比较算法为谷歌提出的Vanilla FL和文献[8]的ESync FL。由结果，非同步FL算法可以获得更高准确率和更快收敛速度。此外，与ESync相比，AFLChain可筛选高质量SN，以达到更好的性能。

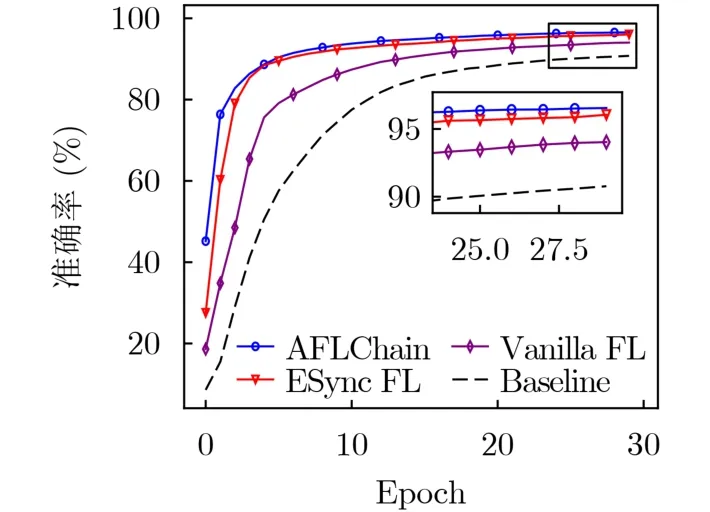
图4 不同算法准确率与全局epoch的关系

如图5所示，本文比较了AFLChain分别采用异步和同步算法时的性能。在FashionMnist上，全局模型为CNN，两者准确率差异不明显，但异步算法能更快达到收敛。在更复杂的通用图片数据集Cifar10上，ResNet18被用作全局模型。相较同步算法，异步算法收敛速度更快，准确率更高。

算法2 基于次梯度的最优资源分配算法(SORA)

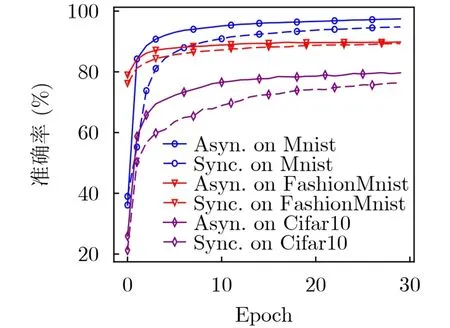
图5 不同FL算法在不同数据集上的性能表现

图6展示了SN数量对算法性能的影响。设目标准确率为95%，达到该准确率的epoch数随着SN数量的增加而减少。当有6个SNs参与训练任务时，与5个SNs所需epoch数相当，因为新加入SN可能算力较低，降低平均算力水平。

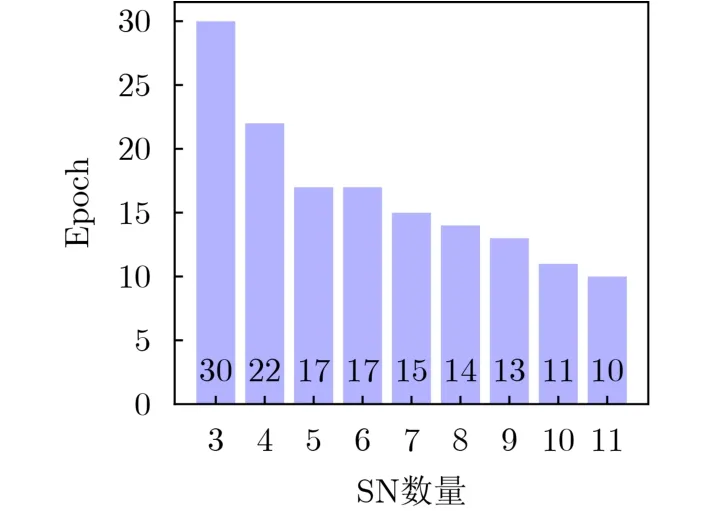
图6 AFLChain在不同SN数量下的性能表现

图7对比了AFLChain在不同算力比ρ下的性能。随着ρ的增大，高算力SNs可进行更多轮次本地训练，对模型准确率提升的贡献更大。ρ=1时，即所有SNs只能完成一轮本地训练时，AFLChain性能等价于同步FL。此外，区块链技术可在不降低训练精度的同时，保证数据安全性和可追溯性。

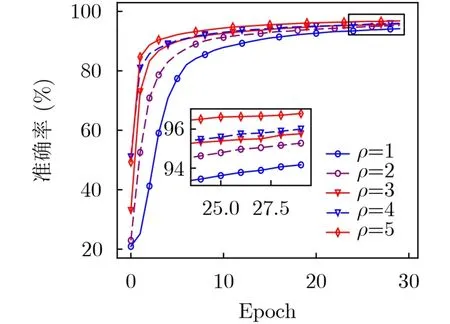
图7 AFLChain在不同算力比时的性能表现

图8描述了不同掉队者比例(低算力SN数量/参与训练SN数量)对算法性能的影响，8个SNs参与FL任务。模型准确率随低算力SN数量的增加而降低，因为低算力SN增多，本地训练轮数相应减少，导致准确率降低。但是，即使掉队者比例大于1/2时，AFLChain仍能达到95%以上的准确率。

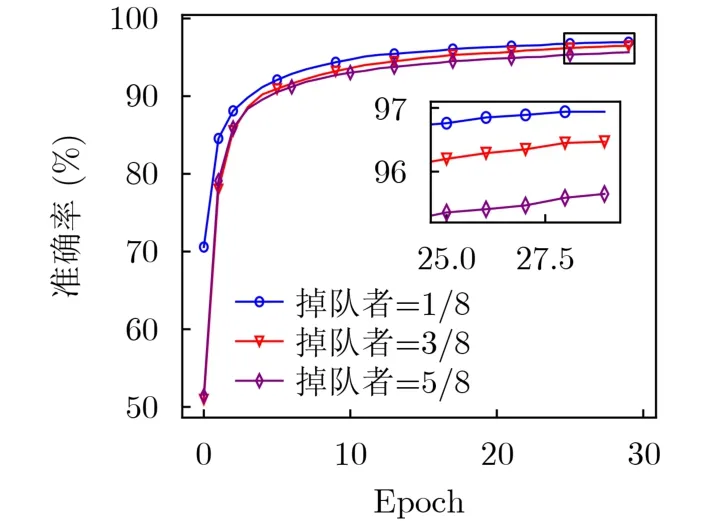
图8 AFLChain在不同掉队者比例下的性能表现

图9对比5种场景到95%模型准确率的性能表现：(1)同步FL，ρ=5；(2) AFLChain，ρ=5；(3)同步FL，ρ=2；(4) AFLChain，ρ=2；(5)同步FL，ρ=1。ρ=5时，同步FL中高算力SN需要等待低算力SN，而AFLChain允许高算力SN在等待时间内持续训练，提高效率效率。ρ=1时，epoch数显著增加，AFLChain等价于同步FL。综上，SN的算力比越高， AFLChain的性能增益越大。

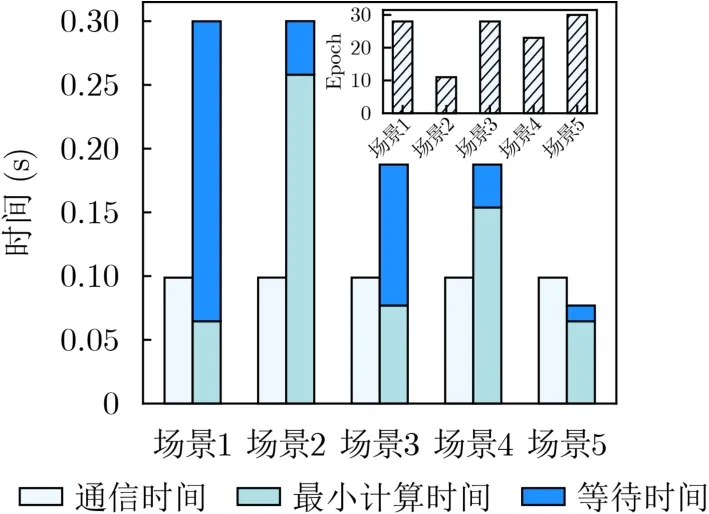
图9 不同算法在不同场景下的时间开销

图10展示了SNs信誉值随着epoch的变化。以SN 3为例，在epoch a，初始信誉值为51＞thupper，为候选SN。在epoch b，其信誉值为16＜thlow，说明它可能出故障，无法继续任务。在epoch c，排除故障或重启后，其信誉值重置为50。在epoch d，其信誉值根据其训练表现有相应升降。每个epoch的领导者由信誉机制选取，避免某个SN的绝对控制。

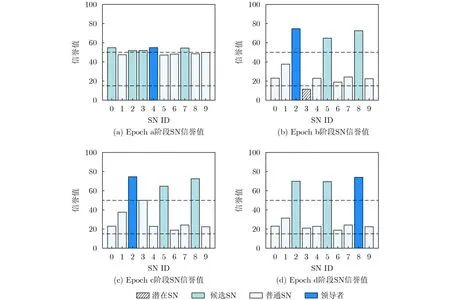
图10 SNs信誉值的变化

图11展示了7个SNs参与任务时，信誉策略对模型准确率的影响。理想场景中，所有SNs均持有高算力且积极训练，不会缺席训练，信誉机制影响极小；非理想场景考虑SNs算力不均且可能掉线，分别对平均权重策略与熵权法策略进行验证。平均权重策略中权重皆为1/3。结果表明，本文所提出的基于熵权法的信誉机制性能接近理想策略。

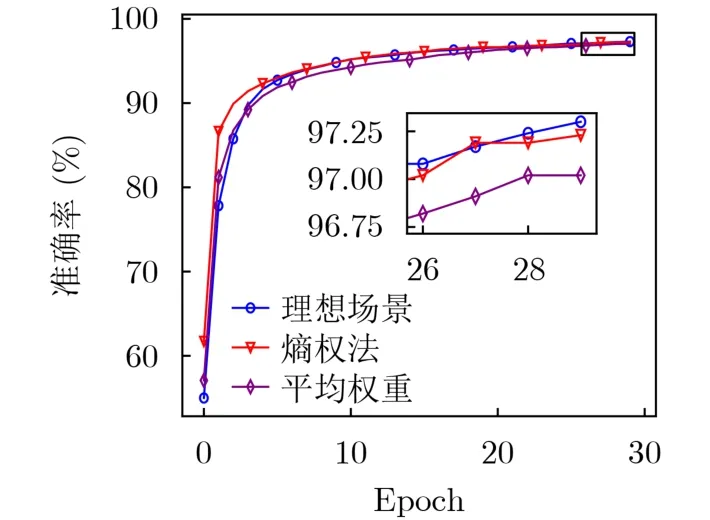
图11 不同信誉机制对准确率的影响

图12显示了SORA算法在不同fmax下的网络时延。SORA算法在分别在迭代8, 10, 12次之后趋于收敛。此外，网络时延随着fmax的增加而降低，因为fmax越大意味着可以分配的计算资源越多， FL任务计算时延和块验证时延也相应降低。

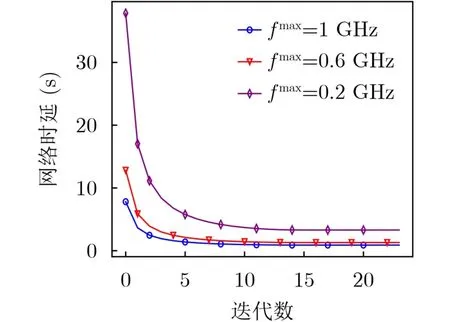
图12 SORA算法在不同最大算力时约束的收敛情况

图13比较了SORA、统一资源分配 (Uniform Resource Allocation, URA)、随机频率分配 (Random Frequency Allocation, RFA)和随机功率分配(Random Power Allocation, RPA) 算法的网络时延。其中，SORA算法性能最好，RFA算法由于计算时延较大，性能最差。RPA算法优化了计算频率分配，训练时间大大减少，性能接近SORA算法。

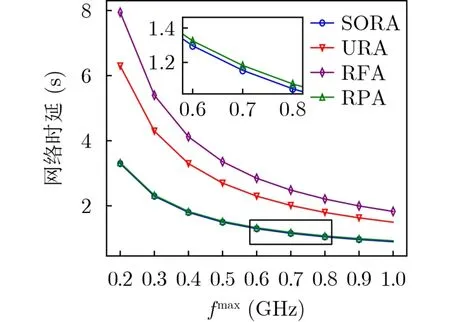
图13 不同资源分配算法的网络时延对比

6 结束语

为提高联邦学习效率，本文提出了一种基于区块链的异步联邦学习算法AFLChain。首先，基于ENs算力分配训练任务，提高计算资源利用率。其次，引入熵权信誉机制评估ENs并对其分级，承担更多训练任务的SN将获得更高信誉值。最后，通过联合优化传输功率和计算资源分配，最小化整体网络延迟。仿真结果验证了所提算法的有效性。