考虑锚节点位置不确定的水下目标定位算法研究

闫 敬 张 婷 尤康林 商志刚 杨 晛 罗小元

①(燕山大学电气工程学院 秦皇岛 066099)

②(哈尔滨工程大学水声工程学院 哈尔滨 150001)

1 引言

水下无线传感器网络被广泛应用于水下目标追踪、辅助导航和海洋数据采集等诸多方面[1]。准确获取传感器节点的位置信息是支持这些应用的基础和关键。目前，水下目标定位技术主要面临以下挑战：其一，由于水下温度与晶振制作工艺的差异，不同类型传感器节点晶振片输出频率不同，存在时钟异步现象。其二，受海水的盐度和压力等影响，声波无法沿直线传播，呈现分层效应。其三，现有定位算法多依赖于测量噪声的先验信息[2,3]，然而水下通信环境恶劣，人为噪声和环境噪声复合后具有随机性和不确定性，并随着测量环境和设备精度的不同而变化[4]，使其具体的统计特性难以确定。其四，受到水体波动等因素影响，某些锚节点位置不确定[5]，引起误差在网络拓扑中的累积传播，导致当前目标节点位置估计的性能下降。

文献[6]考虑锚节点位置不确定的影响，提出了一种基于最大似然估计的定位算法。但该算法严格依赖于噪声的先验信息。文献[7]考虑节点移动性的影响，提出了一种基于最小二乘的定位算法，但该算法容易陷入局部极值。针对局部极值的问题，文献[8]通过使用凸松弛将非凸的目标定位问题转换为凸问题进行求解，然而凸松弛无法完全确保放缩的严密性且转化难度大。近年来，一些研究人员逐渐开始将学习类算法应用到水下目标定位领域。文献[9]提出了一种基于深度Q学习的水下定位算法，将定位问题离散化，在保护隐私的同时完成目标定位任务。然而，深度Q学习依然面临过高估计、样本利用率低和收敛性脆弱等诸多问题[10]。柔性动作-评价(Soft Actor-Critic, SAC)方法引入了熵的概念，使得期望奖励和熵的加权和达到最大时输出最优策略，很大程度上保证了策略的鲁棒性和优越性[11]。

基于上述分析，本文提出考虑锚节点位置不确定的深度强化学习水下目标定位算法。主要贡献如下：(1)提出基于SAC的水下目标定位算法，摆脱了对噪声先验信息的依赖，在锚节点位置不确定情景下完成目标定位任务；(2)设计合理的奖励函数，实现精确定位，并减弱锚节点的位置不确定性；(3)采用层归一化技术，加速深度神经网络学习和收敛，进一步提高模型泛化能力。

2 系统模型

水下无线传感网络包含水面浮标、锚节点和目标节点3种类型的节点。其中，水面浮标不受水下环境的影响，通过全球定位系统获取自身位置并校准时钟。锚节点漂浮在水面以下，可直接与水面浮标通信，用于目标节点定位。由于自身位置精度的限制，其分为精确锚节点和不确定锚节点。目标节点是需要被定位的节点。锚节点与目标节点之间时钟异步，并将目标节点时钟定义为真实时钟。

采用射线追踪法模拟声波的分层效应，获取两节点间的传输时延。依据文献[3]，将水下声速建模为与深度相关的线性函数V(z)=b+az,a=0.017s-1,b=1473 m/s。其中，z为深度，b为水面处的声速，a为与环境相关的常数。

令PS=[xS,yS,zS]T和PR=[xR,yR,zR]T分别为发送节点 S和接收节点 R的位置向量。由Snell定律可得cosθ/V(z)=cosθS/V(zS)=cosθR/V(zR)。其中，θS,θR∈[-π/2,π/2]分别为发送节点 S和接收节点 R处的射线角，进而可导出∂r=∂z/tanθ，∂l=∂z/sinθ，∂t=∂l/V(z)。其中，l为两点间声线长度，t为传输时间，r为水平距离。

由此可以导出发送节点 S和接收节点 R之间的单向传输时延τS,R，表示为

其中，β0=arctan((zS-zR)/rS,R) 为 S点和 R点之间的直线与水平轴的夹角，θS=β0+α0,θR=β0-α0,α0=arctan(arS,R/(2b+a(zS+zR)))为声线偏离角度。

锚节点之间的时钟是完全同步的，但水下目标节点的时钟无法与锚节点完全同步。本文同时考虑了时钟漂移和时钟偏移的影响，表示为

其中，T为本地时钟，t为参考时钟，α和β分别为时钟漂移与时钟偏移。这里，取α=1.005,β=0.002。

3 定位优化问题的建模

3.1 异步通信协议设计

当定位过程开始时，目标节点向整个网络广播消息。传感器节点记为n=1,2,...,N,N ≥3。传感器节点n的位置为(xn,yn,zn)，目标节点的位置为(xM,yM,zM)。

步骤1：初始时刻为TM,M，目标节点 M向锚节点发送定位请求。启动信息包含锚节点的发送顺序n=1,2,...,N。随后，水下目标 M进入监听状态，等待来自锚节点的信息有序传回。

步骤2：在tM,n时刻，锚节点n收到目标节点的信息后，进入监听状态，对来自k=1,2,...,n-1的所有信息进行解码，将到达时间记录为tk,n。节点n接收完来自节点n-1的信息之后，进入发送模式，在tn,n时刻发送自己的信息。节点n发出的信息包含tM,n,{tk,n}∀k，以及发送时间tn,n。

步骤3：水下目标 M在tn,M时刻收到来自锚节点n的回复信息，其中n=1,2,...,N。在接收到最后一个锚节点N的信息后，一轮信息交互完成，收集到的时间戳为

步骤4：基于上述测量值，利用SAC定位算法获取目标节点的水平位置，进而得到3维坐标。

3.2 定位优化问题建立

不同类型节点间的时钟是异步的，因此，为了消除时钟异步现象的影响，定义时间差：

假设定位过程受到统计特性未知但有界的测量噪声干扰，参考文献[12,13]构建以下测量噪声模型，模拟定位过程中未知噪声的干扰。

其中，lS,R是发送节点 S和接收节点 R之间的距离，t是当前迭代步数。

时间差和传输时延之间的关系如下：

其中，ωn,k和ωk,n为测量噪声，分别与对应的发送节点和接收节点间声线传输距离ln,k和lk,n相关。

针对目标节点 M建立如下定位优化问题：

4 基于深度强化学习的水下目标定位算法

4.1 SAC定位算法

SAC算法在目标函数中添加了一个熵项，使得策略的熵和累积奖励均最大化，

其中，H为策略π(at|st)的熵，表示策略的随机性。α为温度系数，控制熵和奖励之间的权重。

基于动作-评价网络架构，采用深度神经网络对Q函数和策略进行拟合，通过随机梯度下降更新网络参数。这里，取最小的Q值来避免过高估计。

算法开始时，初始化策略网络和软Q网络参数，清空经验回放池D。依据以下规则更新参数：

(1)V网络参数：通过残差平方定义损失函数，训练软状态值函数，更新V网络参数。

其中，λ是学习率，是LV(ϕ)的梯度，

对目标Vϕtarget网络的参数进行软更新：

其中，χ为软更新系数。

(2)Q网络参数：用软Bellman残差定义损失函数，训练软Q函数，更新Q网络的参数。

SAC采用重参数技巧，即在原有动作中添加噪声向量ςt～N(0,I)，并使用压缩函数tanh将输出限制在(-1,1)范围内。µφ(st)和σφ(st)分别是策略网络πφ输出的平均值和标准偏差。

因此，方程(14)中的目标函数可以改写为

4.2 算法实现

考虑状态空间和动作空间均连续的情况，记S=[x,y]为状态向量，A=[Δx,Δy]为动作向量。这里，x,y ∈[0 m,100 m], Δx,Δy ∈[-1 m,1 m]。基于此，设置定位任务的整体奖励函数为

其中，rerror=-ρ*Θ(st)为即时奖励，Θ(st)为状态st下的优化目标，ρ为大于零的常数；rpenalty为惩罚项，用于引导目标节点向着奖励增大的方向迭代，加速模型训练；rdone为终止标志，当奖励rt小于阈值ζ时，任务循环结束。这里，

为了提高模型的泛化能力，采用层归一化技术将网络输出转换为固定均值和方差的高斯分布，则第i个通道的归一化输出可以写成如下：

其中，H为一层中隐藏单元的数量，为第i个通道的第l层中的原始输出，ε为添加到分母的偏移量，gi和bi为仿射变换因子。

5 仿真与实验验证

5.1 环境部署

在200 m3的水域中放置3个锚节点A1,A2,A3定位目标节点M 。A1=(200,0,0)和A2=(0,200,0)为精确锚节点，A3为不确定锚节点～N(rA3,K)。其中，rA3=(10,20)为A3的真值，K=diag{5,5}为其方差矩阵。

网络训练的超参数设置如表1所示。

表1 超参数设置

5.2 仿真结果

节点部署与定位结果如图1(a)所示，可知目标节点的坐标收敛至(29.89,79.95, -30)，目标点迭代过程如图1(b)所示。由图1(c)可以看出，改进后的算法在训练速度和稳定性方面均有明显提升。

图1 目标节点定位结果

每个回合对不确定锚节点A3坐标通过求期望进行修正，结果如图2(a)所示。并且，每回合结束时会重置A3的坐标值，将当前回合得到的最佳值复位清除，故其坐标值一直在±0.2 m的小范围内波动。由图2(b)、图2(c)可知，其修正值集中分布在以(10±0.1, 19.9±0.1)为中心的0.1 m2范围内。

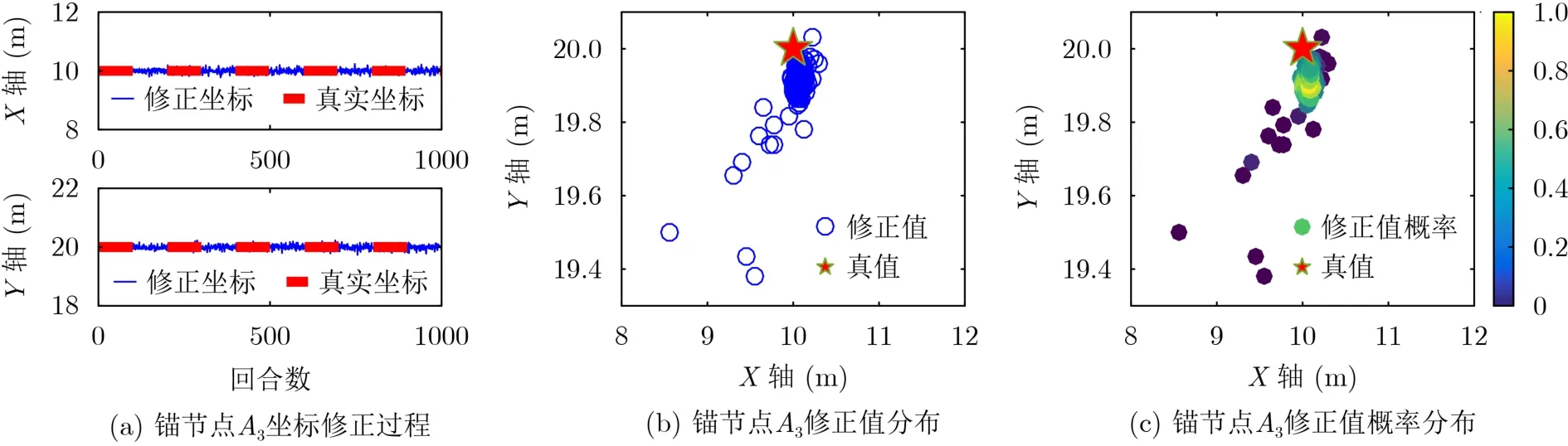
图2 不确定锚节点 A3修正结果

在给定区域内随机采点进行一组和多组测试来验证算法的有效性。一个回合内X轴、Y轴上的定位误差如图3(a)-图3(c)所示。可以看出，171步时done条件被触发，定位任务提前结束，误差收敛到0.35 m以内。15回合内定位结果如图3(d)-图3(f)所示。可以看出，80%的测试点定位精度在1 m以内，其余20%的测试点精度在1～1.2 m。

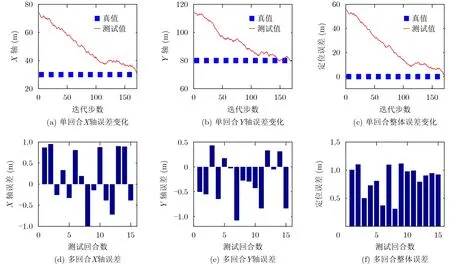
图3 目标节点测试效果

将本文所提定位算法与文献[14]中基于宽度学习的定位算法进行对比。其中，锚节点3为位置不确定锚节点，其余为精确锚节点，仿真结果如图4(a)、图4(b)所示。可以看出，忽略锚节点位置不确定时，文献[14]中算法的定位精度明显下降，而本文所提算法的精度在0.2 m范围内，由此可以看出考虑锚节点位置不确定的必要性。

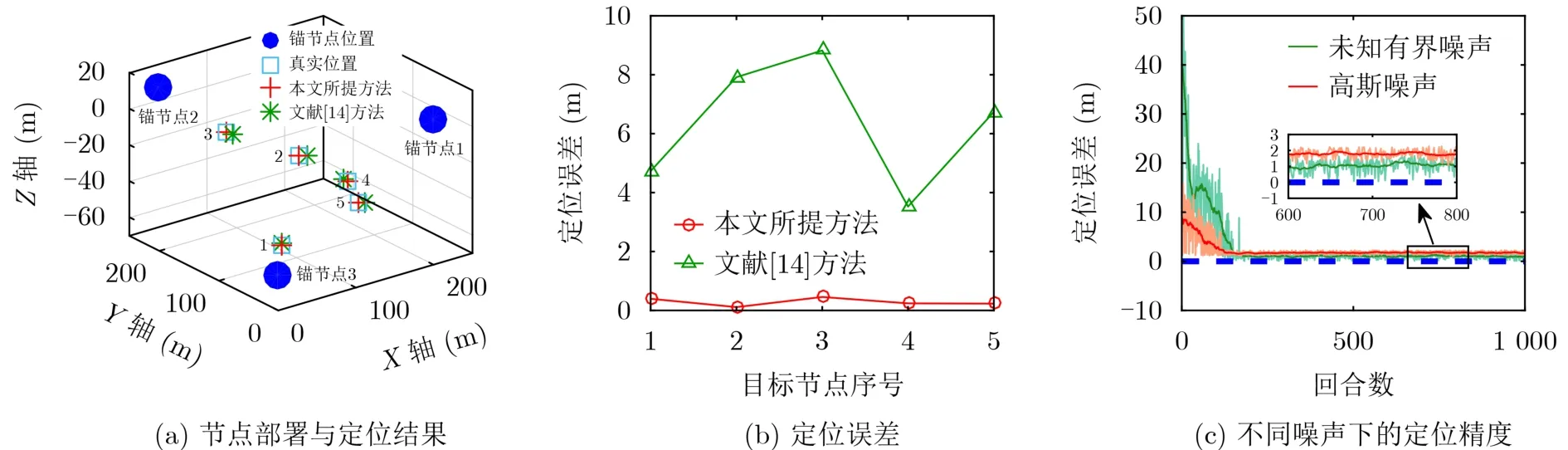
图4 SAC定位算法的优势与适用性

此外，为验证所提算法在不同测量噪声模型下的适应性，分别在文中所提未知有界测量噪声下和高斯测量噪声两种模型下进行验证。这里，采用文献[7]中的高斯测声模型N(0,0.0001)，仿真结果如图4(c)所示。可以看出，两种测量噪声模型下，算法均在200回合之后收敛，且本文的噪声模型下定位精度更高，验证了本文所提定位算法的适应性与有界测量噪声模型的合理性。

5.3 水池实验

在5 × 6 × 1.5 m3的水池中对所提算法进行实验验证。硬件设备主要包括锚节点、目标节点和控制中心3部分。本实验中，将通信机作为锚节点，分别部署于水池中。这里，通信机的工作频带为21～27 kHz，采用正交频分复用模式，稳定通信速率为300 bit/s，最大通信速率为2 000 bit/s。使用水下GPS定位装置(Underwater Global Positioning System, UGPS)对锚节点进行自定位，获取其位置坐标用于目标节点定位。其中，锚节点3为位置不确定锚节点。将UGPS测得的位置作为其真值，在此基础上加入均值为0、方差为0.01的高斯噪声，得到定位过程可用的锚节点3的坐标值。将搭载通信机与深度传感器的有缆遥控水下机器人作为目标节点，可与锚节点通过水声通信方式进行信息交互，并且可直接获取其Z轴信息。将笔记本电脑作为控制中心，操纵机器人移动至不同的位置，模拟对多个目标节点进行定位的过程。同时，将机器人缆线传输的数据输入本文所提的深度强化学习定位算法中定位目标节点。实验平台如图5所示。

由于水池的深度较浅，将声速看作1473 m/s 。对该区域内5个目标节点进行定位，节点分布情况和每个目标节点的定位误差如图6(a)、图6(b)所示。可以看出，相比于文献[7]中基于最小二乘的传统水下目标定位方法，本文考虑锚节点位置不确定影响所提出基于深度强化学习的定位方法整体定位误差较小，精度更高，可以有效完成定位任务，这表明了文中所提算法的实际效用性。

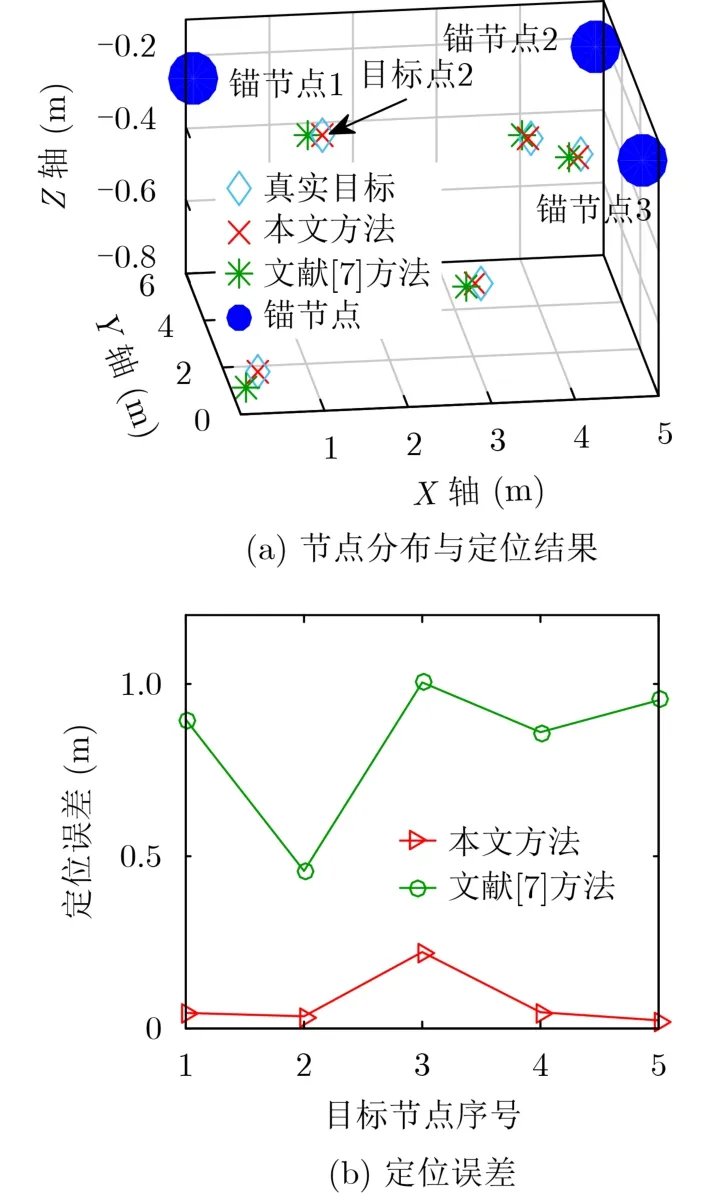
图6 多目标节点定位

6 结束语

本文研究了锚节点位置不确定情景下的目标定位问题。提出了一种基于深度强化学习的水下目标定位算法，完成目标定位的同时可修正不确定锚节点的位置。最后，仿真验证了所提算法的有效性。未来，将研究移动目标节点的定位问题，并通过海洋环境实验对算法的性能做进一步测试。