一种估计最大信息系数阈值最优取值的方法

摘  要：为了简化最大信息系数计算的复杂度，达到计算准确性与计算复杂度的最优平衡，通过基因与疾病相关性实验研究了最大信息系数阈值的合适取值区间及最优取值。结果表明：利用变量间强相关数据和不相关数据出现的频数，及其在不同阈值下的变化趋势，可以估计出阈值的合适取值区间；通过统计阈值取值区间上界集合的最小值，可以估计阈值的最优取值；对于不同变量，阈值的最优取值也不相同，并且随着采样数的增大，阈值的最优取值有减小的趋势。

关键词：最大信息系数；互信息；相关性；阈值；最小最大策略

中图分类号：TP311.1；TP311  文献标识码：A  文章编号：2096-4706（2023）24-0077-05

A Method for Estimating the Optimal Value of Threshold of Maximum Information Coefficient

TAN Zaowen

（Academy of National Space Planning， Hualan Design （Group） Co.， Ltd.， Nanning  530011， China）

Abstract： In order to simplify the computational complexity of the maximum information coefficient and achieve the optimal balance between computational accuracy and computational complexity， the correlation experiment between genes and diseases is used to investigate the appropriate value interval and optimal value of the threshold of the maximum information coefficient. The results show that the appropriate value interval of the threshold can be estimated by using the frequency of strongly correlated data and uncorrelated data between variables and the variation trend under different thresholds. By calculating the minimum value of the upper bound set of threshold values， the optimal threshold value can be estimated; for different variables， the optimal value of the threshold is not the same， and with the increase of the number of samples， the optimal value of the threshold tends to decrease.

Keywords： maximum information coefficient; mutual information; correlation; threshold; Min-Max strategy

0  引  言

最大信息系數（Maximum Information Coefficient， MIC）由Reshef [1]等人在2011年提出，用于解决变量之间的相关性问题。与传统方法相比，最大信息系数具有通用性和公平性的特点，包括：1）对复杂系统具有适应性，能够识别变量之间的线性以及非线性关系；2）泛化能力强，对不完整或有噪声的数据有着抗干扰的能力；3）具有能够分析先验信息的潜力；4）可以对不同类型的数据进行分析，而无须对数据的统计分布（如正态性）进行假设[2]。最大信息系数方法的提出，很好地解决了皮尔森相关系数不能用于非线性相关变量之间相关性的问题。

然而作为一种计算机密集型方法，最大信息系数很难使用手动或者计算器的方式计算得出[3]，即使当前计算机的计算能力已经有了很大的提高，想要计算变量之间的最大信息系数的确切值仍然十分困难。随着变量数据规模的提升，计算最大信息系数所需要迭代的次数将大幅提升，计算的时间复杂度也将迅速增长。

不少学者通过各种方式对最大信息系数进行算法优化，并取得一定程度的效果。曹丹提出了最大信息系数优化估计算法BackMIC[4]，该算法使得网格划分更合理，最大信息系数的估计值更加准确，具有更出色的统计效率和等价性。曹珊将最大信息系数与改进的和声算法结合，提出了两阶段特征选择方法MIC-MHS[5]，该算法能够得到更小的子集，并且能够更高的分类准确率。王月将最大信息系数与K-means聚类算法相结合，提出了适用于海量数据集的MIC聚类算法[6]，提升了计算效率。孟燕霞提出了一种基于动态均分的最大信息系数算法DE-MIC[7]，具有更快的计算速度与更好的效率，同时保持了MIC算法原有的均匀性、普适性。郭园园基于最大相关最小冗余（mRMR）提出了新算法mRMR-ChiMIC[8]，其提取的特征相比于原算法拥有更高的分辨率，同时降低了计算复杂度。邵福波提出了针对大规模数据的最大信息系数快速算法[9]，使得计算时间更短。刘汉明利用全基因关联性研究，提出了MICSNPs、mBoMIC等多种算法[10]，克服了最大信息系数的不足。朱道恒等提出了一种最大信息系数并行算法PCMIC[11]，旨在解决大规模数据下MIC计算时间复杂度高的问题。

为了使最大信息系数能够在较短时间内计算，一个可行方法为限制互信息（MI）计算次数的上限，即阈值，从而简化最大信息系数计算的复杂度，以得出最大信息系数的近似值。本文将通过基因与疾病之间的相关性实验，估计最大信息系数阈值的合适取值区间及最优取值，以达到计算准确性与计算复杂度的最优平衡。

1  关键技术

1.1  皮尔森相关系数

皮尔森相关系数（Pearson correlation coefficient）可以用来计算两个变量之间的相关性[12]。对于两个变量的采样X = {x1，x2，…，xn}，Y = { y1，y2，…，yn}，变量的皮尔森相关系数ρxy为：

为了表示方便，也可以使用皮尔森相关系数的平方  来表示变量间的相关性。但皮尔森相关系数适合用来计算线性相关变量之间的相关性，并不能很好地表达出非线性相关变量之间的相关性。而最大相关系数可以解决这一问题，能够同时计算线性相关和非线性相关变量之间的相关性。

1.2  最大信息系数

最大信息系数是基于互信息[13]（Mutual Information）提出的一种算法。对于两个变量的采样X = {x1，x2，…，xn}，Y = { y1，y2，…，yn}之间的互信息I （X;Y）为：

式（2）为连续型变量的情况下互信息的计算方法，对于离散型变量，互信息Inavive{x; y}的计算公式为[2]：

把所有的（xi，yi）采樣放置到坐标系平面中，将平面沿y方向和x方向分割成nx列和ny行。式（3）中， 表示第i列第j行网格中的散点数量占散点图中所有散点数量的比例， 表示第i列中的散点数量占散点图中所有散点数量的比例， 表示第j行中的散点数量占散点图中所有散点数量的比例。

最大信息系数基于互信息的方法，将式（3）改进为式（4）[2]：

其中，nx和ny分别表示分割成的网格的列数与行数， 表示分成的网格为nx列和ny行时，最大的互信息值，即分成nx列nyny行的网格后，调整行、列之间的距离，找到一个最大的互信息值。

用mx， y表示分成的网格为nx列ny行时的最大信息系数，则最终的最大信息系数为[2]：

其中，N为散点数量，α为阈值，取值为（0，1]。α的取值越大，最大信息系数越准确，但计算复杂度也会大幅上升，因此有必要将α限制在一个合适的区间里，以达到计算准确性与计算复杂度的最优平衡。

1.3  最大信息系数网格分割过程

由上一章节可以看出，在求最大信息系数的过程中，需要对采样所在的坐标系平面沿y方向和x方向进行分割，从而计算互信息值。如图1所示：

从图1可以看出，坐标系平面沿y方向和x方向被分割成2×2的网格，以下称为m2，2，其中不同颜色的线代表不同的网格分割方法（图1中只展示出其中3种划分方法）。我们需要找到m2，2下使得互信息取得最大值的划分方法，进而求出m2，2对应的最大信息系数MIC2，2{x，y}。

然后将坐标系平面沿y方向和x方向分割成2×3（或3×2）的网格，即m2，3（或m3，2），并求出其最大信息系数MIC2，3{x，y}（或MIC3，2{x，y}）。以此类推，直到nx ny = N α为止。最后，找到所有最大信息系数中的最大值，作为最终的最大信息系数，即式（5）所示。

2  实验分析

2.1  实验数据

本文利用基因与疾病之间的相关性实验，来估计最大信息系数阈值α的最优取值。

本实验使用的数据存放在csv文件中。文件每一行表示一种基因，列上有多种疾病的探针采样，有患病的和未患病的采样作为对照。可以从列标签看出，N前缀表示未患病，T前缀表示患病。后缀数字表示同一种疾病的不同采样。每个采样（列）中，不同基因的表达程度可以从单元格中读出。

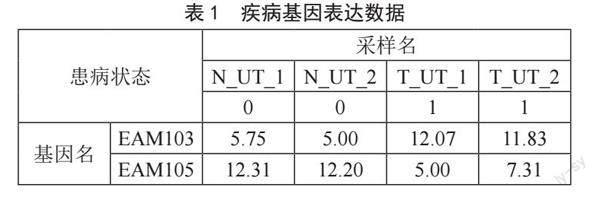
需要对每个基因、每种疾病分别进行最大信息系数的计算。对于某种基因、疾病，将患病状态作为y值，0表示未患病，1表示患病，将对应的基因表达程度采样值作为x。如表1所示（此处仅列出部分数据）。

表1展示了UT疾病的部分基因表达数据，每行表示不同的基因，N前缀列表示未患UT疾病的采样，即对照组，T前缀列表示患UT疾病的采样。表中的数值表示某个基因在对应采样中的表达程度，数值越高，表达程度越明显。

表1的第二行表示该列采样是否患病，1为是，0为否。对该疾病的基因画散点图，一般会有以下几种情况，如图2所示。

从图2中很难直观地得出基因与疾病之间的相关性程度，但可以根据图中散点的分布情况得出，在基因与疾病之间具有较强相关性的情况下，它们的关系是正相关还是负相关。具体方法如下：设P = { pr，i | i ∈ [1，nr]，r = 0，1}为某个基因相对于某个疾病的散点图上所有的点，例如图2所示，每个散点表示一个探针。其中r = 0，1分别表示未患病和患病的类别标签，nr表示该类别的探针数量。令 ，表示类别为未患病的所有探针的表达程度平均值，，表示类别为患病的所有探针的表达程度平均值。如果 ，则该基因与该疾病的相关性为正相关；反之，如果 ，则该基因与该疾病的相关性为负相关。值得注意的是，从本质上来说，当 时，基因与疾病之间的关系应为无关，或相关性不大，但这里仅仅讨论如何区分正负相关性，基因与疾病是否相关，或者相关的程度，应通过计算最大信息系数得出。

部分基因的散点图与图2中的EAM185类似，患病状态为0的点的平均值 ，在患病状态为1的点的平均值  的左侧，即 ，可以认为该基因与疾病之间的相关性为正相关。部分基因的散点图与图2中的EAM192类似，患病状态为0的点的平均值 ，在患病状态为1的点的平均值  的右侧，即 ，可以认为该基因与疾病之间的相关性为负相关。部分基因的散点图与图2中的EAM103类似，患病状态为0的点的平均值 ，与患病状态为1的点的平均值  近似，即 ，可以认为该基因与疾病无关，或相关性不大。

2.2  最大信息系数和阈值的关系

仍以UT疾病下，EAM103、EAM185、EAM192这三个基因举例，观察最大信息系数的结果和阈值 的关系。我们将 在 之间，每隔一小段距离取一个值，计算该值下这三个基因的最大信息系数，获得基因与疾病间的最大信息系数随阈值 变化的情况。如图3所示。

从图3中可以看出，EAM103基因最终的最大信息系数较低，为0.656，这印证了2.1章节所述的假设，EAM103基因和UT疾病的相关性不大；EAM185基因、EAM192基因最终的最大信息系数较高，分别为0.808、0.998，这也印证了2.1章节所述的假设，EAM185基因、EAM192基因和UT疾病有较强的相关性。从原始数据中还可以看出，EAM185基因与UT疾病之间的相关性为正相关，EAM192基因与UT疾病之间的相关性为负相关。

结合图3中的三条折线，还可以推断出，当阈值α取值较小时，最大信息系数的取值也较小，并且几乎不变化；当α大于某个值时，最大信息系数开始变化并增大；当α继续增大，再次超过某个值时，最大信息系数的增长达到极限，此时的最大信息系数为最终的、也是最准确的最大信息系数。

可以看出，当阈值α增大到某个程度时，继续增大阈值，最大信息系数的变化程度将变得不明显，但此时的计算复杂度仍然在明显增大。因此，有必要为阈值α确定一个合适的取值。

2.3  阈值的合适取值区间估计

本文使用以下方法估计阈值α的合理取值。

记nx为横坐标的网格数，ny为纵坐标划分的网格数，B表示最大的网格总数即nxny≤B，其为样本数量的函数，记B = N α，N为样本数量，α为阈值参数。对于阈值α，Reshef等人[1]只提供了參考的经验值0.60或0.55，但网格的疏密度会直接影响到最优的最大信息系数值，因此对于不同的样本，需要估计不同的阈值α，从而提高最大信息系数的最优度。

假定当最大信息系数值小于0.1时，X和Y是不相关，该条件下记为A1，当MIC值大于0.9时，X和Y是强相关，此条件下记为A2。仍然使用UT疾病数据，统计出A1和A2在不同的阈值α ∈ [0.2，1.0]下对应的基因出现频数。如图4所示。

从图4中可以看出，在α = 0.6时，A1对应的基因频数开始有下降的趋势，而A2对应的基因频数则开始出现上升的趋势，在α = 0.73时，二者有一个交点，继续增大α，A1状态变化不明显。因此可以认为在该样本下，阈值α设置在[0.6，0.73]之间是比较合适的。

2.4  阈值的最优取值估计

在估计出阈值α合适的取值区间后，本文还将继续探讨如何估计阈值α的最优取值。

对某一疾病下，所有基因的最大信息系数在阈值α ∈ [0.2，1.0]的范围内进行迭代，获得所有的基因与该疾病的最大信息系数阈值α的取值区间。由于最大信息系数随α变化的曲线并不平滑，本文使用如下方法求出阈值α的取值区间：

对于每个基因，以最大信息系数开始变化的值作为阈值α的取值区间下界αmin，以最大信息系数停止变化的值作为阈值α的取值区间上界αmax，则区间[αmin，αmax]即为所求的阈值α的取值区间。仍以UT疾病为例，部分数据表2所示。

由于不同基因之间的阈值α取值区间下界αmin过于近似，本文使用阈值α取值区间上界αmax的最小值，即最小最大策略，作为阈值α的最优取值，结果为0.61。

对其他疾病也进行同样的实验，获得更多的阈值α最优取值，仍然使用最小最大策略，结果如表3所示。

从表3中可以看出，不同疾病下，阈值α的最优取值也不相同。并且随着采样数的增大，阈值α的最优取值有减小的趋势。

3  结  论

最大信息系数之所以近年来才被发现，是因为它实际上是为大数据而生的一种典型的计算机密集型方法的应用，旨在加强大数据下的统计相关性研究。

本文利用基因与疾病之间的相关性实验，估计出最大信息系数阈值α的合适取值区间及最优取值，并得到如下结论：1）最大信息系数具有很好的广泛性和均匀性，能够识别变量之间的非线性以及非线性关系；2）对最大信息系数阈值α进行合理的取值，能够达到计算准确性与计算复杂度的最优平衡；3）利用变量间强相关数据和不相关数据出现的频数，在不同阈值α下的变化趋势，可以估计出阈值α的合适取值区间；4）通过统计阈值α的取值区间上界集合的最小值，可以估计阈值α的最优取值；5）对于不同变量，阈值α的最优取值也不相同。并且随着采样数的增大，α的最优取值有减小的趋势。

参考文献：

[1] RESHEF D N，RESHEF Y A，FINUCANE H K，et al. Detecting novel associations in large data sets [J].science，2011，334（6062）：1518-1524.

[2] 武利园，潘宇霖，陈开宇，等.基于最大互信息系数的城市节水驱动因素分析 [J].人民黄河，2023，45（1）：87-92.

[3] 孟燕霞，郭禹辰，王莉.一种基于动态均分的最大信息系数改进算法 [J].山东大学学报：工学版，2019，49（5）：105-111.

[4] 曹丹.最大信息系数优化算法及在生物信息学中的应用 [D].长沙：湖南农业大学，2020.

[5] 曹珊.最大信息系数与改进的和声算法相融合的特征选择方法 [D].长春：吉林大学，2020.

[6] 王月.最大信息系数的算法分析及改进 [D].西安：西安电子科技大学，2019.

[7] 孟燕霞.最大信息系数算法研究 [D].太原：太原理工大学，2019.

[8] 郭园园.基于互信息的信息基因选择算法研究 [D].长沙：湘潭大学，2018.

[9] 邵福波.最大信息系数改进算法及其在铁路事故分析中的应用 [D].北京：北京交通大学，2016.

[10] 刘汉明.基于最大信息系数的复杂疾病全基因组关联算法研究 [D].成都：电子科技大学，2015.

[11] 朱道恒，李志强.最大互信息系数的并行计算方法研究 [J].科学技术与工程，2021，21（34）：14625-14633.

[12] 尹欢一.基于皮尔森系数距离权重KNN算法的P2P流量分类方法研究 [D].株洲：湖南工业大学，2019.

[13] 闵捷.基于互信息极大化的多时相遥感影像分类算法研究 [D].西安：西安电子科技大学，2022.

作者简介：谭藻文（1993—），男，汉族，广西南宁人，系统分析师，硕士，研究方向：计算机技术、数据挖掘、人工智能、地理信息系统。