塔筒安装条件下法兰盘受力变形分析研究
龚 欢,卫红英,叶兆艺,王欣怡,李小鹏
(1.中国电建集团华东勘测设计研究院有限公司,浙江杭州311100;2.浙江华东工程咨询有限公司,浙江杭州311100;3.浙江大学港口海岸与近海工程研究所,浙江杭州310058;4. 锡林浩特市泰富风力发电有限公司,内蒙古锡林浩特026099)
0 引 言
随着全球对可再生能源的需求不断增加,风电作为一种具有潜力的清洁能源,其重要性逐渐凸显出来[1]。相比于传统的能源形式,如化石燃料,风电具有零排放、无污染等优势。
法兰盘是连接塔筒的关键组成部分,通常由高强度钢材制成[2]。塔筒翻身吊装施工过程中,法兰盘及螺栓孔容易发生损伤变形,导致螺栓连接失效,严重影响塔筒的安全稳定性。目前已经有学者对塔筒法兰盘进行了相关研究[3-7],樊轲等[3]通过模型试验以及有限元软件对高强度铆钉的疲劳特性进行研究,发现该高强铆钉能有效提升抗疲劳性能。李勇芝等[4]采用ANSYS有限元软件研究了不同法兰防变形支撑结构对法兰变形的影响规律,研究表明三字支撑结构防变形效果最好。张卜铜等[5]针对法兰盘焊接后出现微小变形导致连接螺栓应力集中的问题,提出了一种热矫正工艺。林定果等[6]采用EasyLaser平面度分析软件,分析了下料误差对塔筒法兰平面度的影响,提出控制下料误差的方法以解决法兰平面度超标问题。胡良明等[7]通过ABAQUS对带有法兰螺栓的塔筒结构进行结构振动特性研究,得到一种快速检测螺栓断裂的理论方法。
近年来,风电机组的额定功率已经从2 MW逐步提升到10 MW以上[8-10],高功率风力机组需要更高、更重的塔筒;对塔筒的吊装也提出了更高的要求,工程中经常出现吊装导致法兰盘上的螺孔变形使得塔筒上下端连接不紧密等问题。但是目前对塔筒吊装翻身时塔筒法兰以及螺孔的受力变形特征研究较为匮乏。
本文以吊装条件下的法兰盘为研究对象,基于有限元软件ABAQUS,建立塔筒及法兰盘三维数值模型,分析塔筒翻身吊装过程中法兰盘螺孔变形特征,研究结果可为塔筒安全吊装施工提供理论支持。
1 塔筒吊装施工工艺
塔筒吊装施工是风电工程建设重要的组成部分。施工工艺为主吊车起吊上法兰,辅助吊车起吊下法兰,对塔筒进行抬吊翻身。两台吊车协调工作,防止法兰与地面接触,直到辅吊端法兰朝下,卸掉塔同底部辅吊端吊座组件。其中,主吊端法兰面安装4个吊耳,辅吊端法兰面安装2个吊耳,并用高强度螺栓紧固。此外,安装专用吊带、钢丝绳和滑车组件等,如图1所示。塔筒吊装翻身时,结构组件受力分析如图2所示。
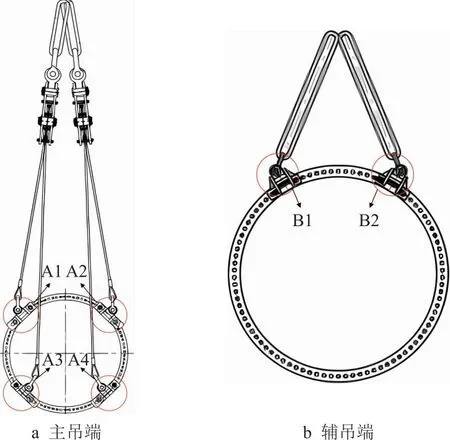
图1 法兰盘吊耳安装位置

图2 塔筒翻身吊装受力分析示意
2 塔筒及法兰盘有限元模型
2.1 有限元模型参数设置
基于塔筒及法兰盘的实际尺寸建立模型,其中,塔筒长28.1 m,直径4.238 m,塔筒壁厚0.06 m。法兰盘外径4.678 m,厚0.22 m,宽0.2 m,法兰盘上有96个螺孔,其中螺孔中心距法兰盘外径0.08 m,螺孔直径0.06 m。塔筒及法兰盘有限元模型见图3。采用八结点线性六面体单元(C3D8R)对网格进行划分。模型材料设为弹塑性材料,质量密度7 850 kg/m3,弹性模量206 GPa,泊松比0.3;塑性参数见图4。

图3 塔筒及法兰盘有限元模型
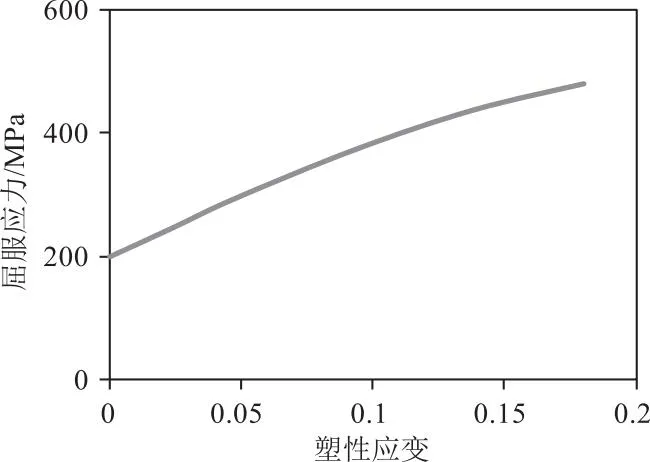
图4 模型塑性特征[11]
2.2 边界条件及加载方式
考虑塔筒翻身过程中,主吊端向上偏转,因此,将辅吊端的两个吊点进行约束,对吊点B1设置3个方向的约束,对吊点B2设置水平和竖直方向的约束。对模型整体施加重力,主吊端的吊点采用表面荷载进行加载。边界条件以及荷载施加方式,如图3所示。
3 水平条件下法兰盘受力特征分析
3.1 应力分析
图5为塔筒水平状态时法兰盘的Mises应力云图。从图5可以看出,主吊端法兰盘上应力集中主要发生在A1、A2、A3、A4等4个吊点以及法兰盘上下端。辅吊端应力集中主要发生在B1、B2等2个吊点。从法兰盘上端沿圆周分别绘制主吊端及辅吊端法兰盘的应力曲线,绘制方向如图5箭头所示,所得应力曲线见图6。

图5 法兰盘应力云图
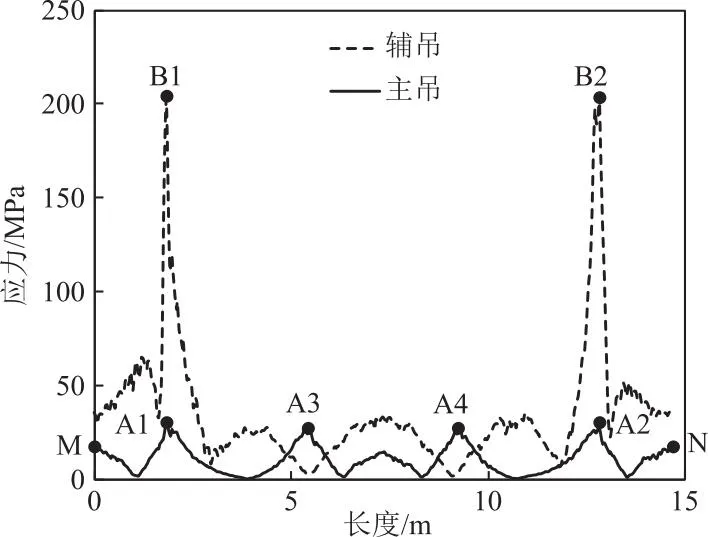
图6 法兰盘应力曲线
从图6中可以看出,主吊端吊点A1与A2应力为30.0 MPa,吊点A3与A4的应力为26.8 MPa。主吊端法兰盘的上端以及下端也出现了应力集中现象,上端应力为17.2 MPa,下端为14.5 MPa。吊点A1、A2处的应力约为吊点A3、A4处的1.12倍,主吊端法兰盘上端应力约为下端应力的1.19倍;辅吊端吊点B1与B2的应力均为211.7 MPa,约为主吊端吊点A1的7倍。辅吊端法兰盘的上下端应力集中现象不明显,但整体应力远大于主吊端,最危险点为辅吊端的两个吊点。
3.2 应变分析
上述应力分析表明,辅吊端法兰盘为危险端,且该端的吊点B1、B2为最危险点,因此,提取辅吊端法兰盘以及吊点B2的应变云图,见图7。
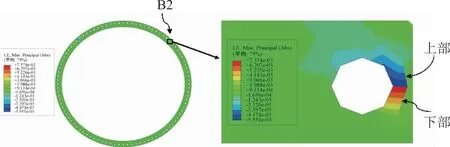
图7 辅吊端法兰盘及螺孔应变云图
从图7中可以看出,辅吊端法兰盘整体应变分布均匀,吊点B2处螺孔下半部分应变值最大值为0.007 4,螺孔上半部分应变最大值为-0.005 6,说明螺孔上半部分受压,下半部分受拉,螺孔整体发生剪切变形。
图8显示B2处螺孔的等效塑性应变(PEEQ),等效塑性应变区域集中在螺孔中心到法兰盘中心的另一侧,等效塑性应变PEEQ的峰值约为0.006 4,说明该处已经发生屈服。

图8 螺孔等效塑性应变应变云图
图9为辅吊端法兰盘位移云图。从图9中可以看出,辅吊端法兰盘水平方向沿中间压缩5.08 mm,竖直方向沿上下两端拉伸4.76 mm。从中可以提取B2吊点处螺孔位移为0.55 mm。

图9 辅吊端法兰盘位移云图
4 不同倾角条件下法兰盘受力特征分析
4.1 应力分析
开展塔筒由水平翻身至竖直状态的过程中法兰盘受力特征分析。设置倾角为0°、30°、45°、60°、90°5组工况,研究不同翻身阶段时法兰盘及螺孔的受力变形特征。其中,在倾角为90°工况时,辅吊端吊耳拆除,仅有主吊受力,因此对边界条件重新设置为主吊端吊点A2、A3、A4约束方向上的位移,吊点A1约束3个方向上的位移,模型整体受到竖直向下的重力。
图10为不同工况法兰盘的应力云图,从图10可以看出,主吊端法兰盘最大应力在倾角为30°、45°、60°、90°时为31.2、29.5、26.3、200.3 MPa;辅吊端法兰盘最大应力为208.2、204.7、202.3、0.3 MPa。在吊装至垂直状态,拆除辅吊端吊耳前,随着倾角的增大,主吊端和辅吊端法兰盘应力均减小,主吊端的最大应力远小于辅吊端。但是当吊装至90°时,吊耳拆除,此时辅吊端应力趋近于0,应力主要集中在主吊端4个吊点上。
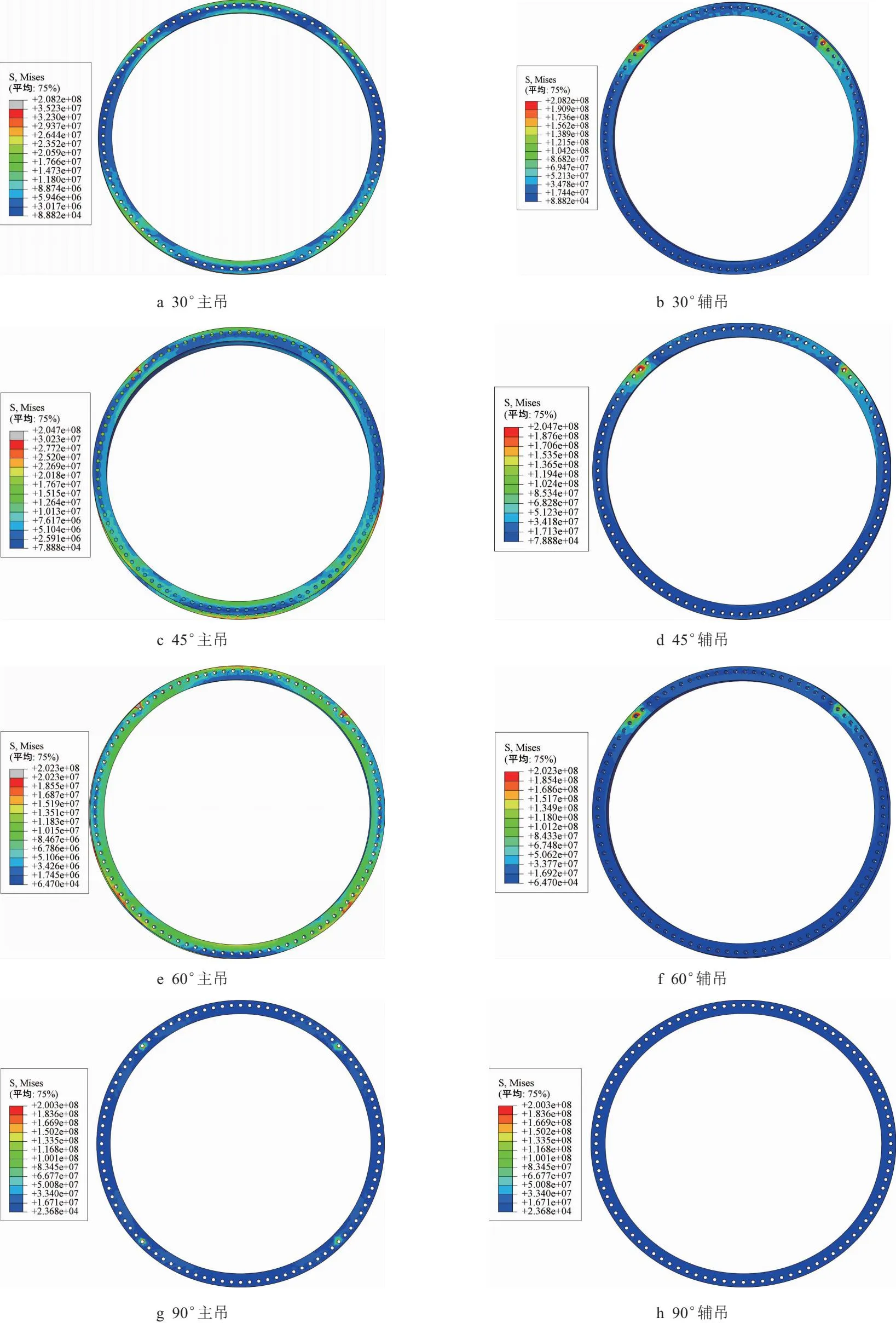
图10 不同工况法兰盘应力云图
4.2 应变分析
由图11可知,在塔筒倾角90°之前,辅吊端应力最大,在90°时,主吊端应力最大。因此提取30°、45°、60°工况下的辅吊端法兰盘及螺孔应变云图以及90°工况时的主吊端法兰盘及螺孔应变云图,见图11。

图11 不同工况法兰盘及螺孔应变云图
从图11可以看出,倾角为30°、45°、60°时辅吊端螺孔的塑性应变的值分别为0.004 2、0.002 4、0.001 5,在倾角为90°时,整体塑性应变为0,因此选取提取主吊端螺孔的弹性应变,值为0.001。在90°之前,随着倾角的增大,辅吊端螺孔的塑性应变逐渐减小,均为上半部分受压,下半部分受拉,说明在塔筒翻身阶段,辅吊端螺孔始终发生剪切变形。在吊装至90°时,主吊端螺孔边缘应变为正值,说明螺孔周围发生拉伸。提取辅吊端吊点B2处的螺孔位移变形,以及主吊端吊点A1处的螺孔位移变形,如表1所示。

表1 不同工况辅/主吊端螺孔变形
从表1可知,随着倾角的增大,辅吊端螺孔的变形逐渐减小,在0°时最大为0.55 mm,当吊装至竖直状态时,主吊端螺孔变形达到整个吊装翻身阶段的最大值为0.15 mm,为辅吊端螺孔最大变形值的27%。上述分析表明,整个塔筒吊装过程中,法兰螺栓孔最大变形发生在塔筒水平起吊时。
5 法兰螺孔变形预测公式
由于风电机组的功率及样式不同[12-13],所需的塔筒及法兰盘的几何尺寸各不相同,需要对不同塔筒及法兰盘尺寸进行敏感性分析。得到塔筒壁厚T,法兰盘厚度W以及塔筒长度L对法兰盘螺孔最大变形的D的影响规律,通过非线性拟合方法[14],建立螺孔最大变形与塔筒及法兰盘几何尺寸的预测公式,并验证公式的准确性。
5.1 敏感性分析
从表1可知,当塔筒处于水平状态时,辅吊端B2处螺孔变形最大,因此基于辅吊点B2处的螺孔变形开展塔筒及法兰盘几何尺寸敏感性分析。敏感性分析的参数取值范围如下:法兰盘厚度W取18、20、22、24 cm;塔筒长度L取26、28、30、32 m,塔筒壁厚T取6、8、10 cm,共计48组工况,部分敏感性分析结果如图12所示。从图12可以看出,法兰盘螺孔的最大变形随塔筒壁厚及塔筒长度增大而增大,随法兰盘厚度增大而减小。

图12 螺孔最大变形的影响因素
5.2 螺孔变形预测公式
通过非线性拟合方法[14],分析48组工况的分析结果,建立基于塔筒壁厚T、法兰盘厚W、塔筒长度L等3个变量的法兰盘螺孔最大变形D的预测公式,即建立函数关系D=f(T,W,L),具体公式为
D=(-0.017 4WL+0.437L+0.41W-10.3)T+0.056 3WL-1.4L-1.3W+32.33
(1)
式(1)的可靠性分析结果如图13所示。通过对比实际螺孔变形数据和公式(1)预测变形数据,结果显示公式(1)计算所得的法兰盘螺孔最大变形平均误差仅为6.79%,可以为吊装条件下法兰盘螺孔最大变形预测提供有效的理论支持。
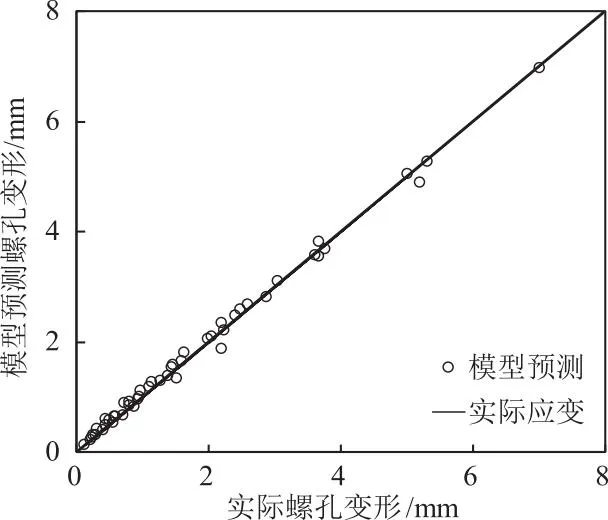
图13 预测模型可靠性验证
6 结 论
采用有限元数值模拟方法,开展塔筒吊装翻身时法兰盘受力特性研究,得到如下结论:
(1)塔筒吊装翻身过程中,当塔筒处于水平状态下法兰盘所受应力变形最小。辅吊端吊点最大应力约为主吊端吊点的7倍;法兰盘螺孔上半部分受压,下半部分受拉,螺孔局部屈服,出现剪切变形。
(2)塔筒法兰盘几何参数盘敏感性分析显示,法兰盘螺孔的最大变形随塔筒壁厚及塔筒长度增大而增大,随法兰盘厚度减小而增大。
(3)基于敏感性分析数据,提出了基于非线性拟合方法的法兰盘螺孔最大变形预测公式,平均误差仅为6.79%,可以为吊装条件下法兰盘螺孔最大变形预测提供有效的理论支持。

