基于高速摄影的直角壁面附近柱形空泡动力学行为研究1)

吴冠豪 苏泓臣 王笑语 张宇宁 李惊涛

(华北电力大学电站能量传递转化与系统教育部重点实验室，北京 102206)

(华北电力大学能源动力与机械工程学院，北京 102206)

当空化现象发生在水力机械壁面附近时[1]，空化泡溃灭产生的射流冲击将会对壁面造成严重损害[2-4]，极大影响水力机械的安全运行。水力机械内部壁面类型多样复杂，其中角形壁面广泛存在，例如：阀门[5]、泵[6]、管道弯头[7]等。而当角形壁面位于比较狭窄的液体流动通道处时，由于受到狭窄流道的约束，空泡往往会呈现出圆柱形的形态。尽管与一般的球形空泡形态不同，但是柱形空泡溃灭时对壁面造成的损害依然是存在的。因此，本文基于高速摄影实验系统地分析了直角壁面附近柱形空泡的动力学特性。

目前，关于直角壁面附近空泡动力学的研究以球形空泡为主。Brujan 等[8]研究了直角壁面附近激光诱导空泡的动力学行为，发现空泡溃灭阶段会产生液体射流，并且空泡会沿着射流方向移动，而射流方向与空泡初始位置和壁面的距离有关。Tagawa 等[9]基于势流分析简要构建了溃灭射流速度和方向的表达式，用来预测射流的方向和空泡的位移，用实验中获得空泡射流方向数据对理论模型进行了验证，并将其理论模型扩展到了不同角度的锐角壁面。而对于柱形空泡的研究目前相对较少，Zwaan 等[10]应用实验初步展示了平壁面附近柱形空泡的溃灭过程，定性研究了微射流及其诱导的气泡分裂和空化云旋转现象，并将其扩展到了更复杂的几何形状（例如：封闭三角形和正方形等）附近柱形空泡的液体射流情况。此外，Chen 等[11-12]通过实验研究了窄缝中稳定的微气泡附近另一个激光诱导空泡的溃灭行为及它们之间的相互作用，发现后者的正向射流引起前者的各向异性压缩，并使其在复杂作用下破碎成更小的气泡。而当两者间距较小时，前者的作用使得后者在溃灭阶段产生反向射流。综上所述，目前对于壁面附近柱形空泡动力学的研究尚有不足。主要表现在以下两点：（1）相对于球形空泡来讲，柱形空泡的稳定生成手段相对复杂，空泡的位置和半径等参数难以准确控制，导致难以实现系统和参数化的研究；（2）关于柱形空泡动力机制的研究还不够深入和完善，柱形空泡在溃灭过程中形态和位置变化的规律还没有被揭示。本文将针对上述问题进行深入研究。

本文基于高速摄影实验，探究了直角壁面附近柱形空泡动力学行为，分别对空泡位于对称位置和非对称位置的情况进行了分析。各小节安排如下：第1 节介绍了高速摄影实验系统、实验参数，进行了误差分析，验证了实验的可重复性，展示并分析了一个典型实验结果的高速摄影图像；第2 节分析了对称位置处典型柱形空泡高速摄影图像及其对应的空泡形态变化规律和动力学机理、溃灭过程中的空泡圆度变化以及空泡形心移动距离变化；第3 节分析了非对称位置处典型柱形空泡高速摄影图像及其对应的空泡形态变化规律和形心移动方向变化；第4 节总结了本文的主要工作，并进行了展望。

1 高速摄影实验系统与参数

本节主要介绍了高速摄影实验系统布置、基本的实验流程以及实验模型相关参数。进行了误差分析，验证了实验的可重复性。然后展示并分析了一个典型位置的柱形空泡高速摄影实验结果。

图1 是实验系统的示意图。实验系统主要由高速摄影机、数字延迟发生器、激光发生器、聚焦透镜、水箱、光源、三维平移台、电脑等组成。其中，高速摄影机型号为千眼狼高速摄影机X113系列，本次实验拍摄速度为47 619 帧/s，相邻两帧之间的时间隔为Δt= 21.00 µs；数字延时发生器型号为斯坦福DG535，最高能达到5 ps 延迟分辨率；激光发生器型号为Penny-100A-SC，最大能量为100 mJ，本次实验采用波长为532 nm的平行激光；聚焦透镜放大倍率为20×。如图1所示，在实验过程中，通过数字延迟发生器使得激光发生器发出规律性的平行激光，并通过透镜将激光聚焦于水箱。水箱中的实验模型被浸没在去离子水中，由两块平行玻璃板及被夹在中间的直角壁面构成。激光聚焦于直角壁面以及两块平行玻璃板之间的狭小液体区域，并诱导形成空泡。由于平行玻璃板间距较小，空泡在振荡的过程中将会受到前后两侧玻璃板的限制，两侧泡壁总是紧贴玻璃板，从而表现为近似柱形的特性。调整光源位置和强度，保证高速摄影机拍摄画面清晰可见。使用电脑控制高速摄影机拍摄柱形空泡完整的振荡过程，并将实验数据保存在电脑上。通过调节三维移动平台可以控制直角壁面与柱形空泡的相对位置关系，从而得到本文分析的包括直角壁面对称和非对称位置处柱形空泡的多组实验数据。

图1 实验系统图Fig.1 Experimental system diagram

图2 展示了实验模型中的一些重要参数，其中图2(a)是模型的正视图，即高速摄影机拍摄的方向，图2(b)是右侧视图。在图2(a)中，Rmax是柱形空泡第一周期的最大半径，本文Rmax=1.15 mm。Z0是柱形空泡最大半径时刻的形心位置。l是柱形空泡形心Z0与直角壁面顶点O的距离。θ 是l与X轴正方向的夹角，用来表示柱形空泡所在的位置角度。θk表示柱形空泡形心在溃灭过程中的移动方向与竖直方向的夹角。在图2(b)中，h为两玻璃板之间的间距，本文h= 1.5 mm。

图2 实验参数图：（a）正视图，（b）右侧视图Fig.2 Experimental parameter diagram: (a) front view,(b) right-side view

为方便后续定量分析，定义无量纲距离l*

本次实验得到的高速摄影图像的比例尺为0.073 7 mm/pix。在后续对实验数据进行分析时，即对柱形空泡轮廓进行取点时，存在人为误差。最大误差计算为

式中，ΔX和ΔY为分别为取点时横轴和纵轴上的误差值，为一个像素点的宽度；ΔC为最大误差。

此外，对同一位置处的柱形空泡进行了多次实验，并挑选了其中一组，将其形心位置和最大空泡半径等数据统计在表1 中，然后分别得到其对应的相对误差大小。可以发现，本次实验中同一位置处柱形空泡形心位置和最大空泡半径的相对误差均小于3%，在误差允许范围之内，因此本次实验具有较好的重复性。

表1 实验相对误差统计表Table 1 Statistical table of experimental relative error

表1 中，X0，Y0为柱形空泡出生时刻的横、纵坐标的测量数据。ΔX*，ΔY*为柱形空泡出生时刻横、纵坐标的相对误差。ΔRmax*为柱形空泡最大半径的相对误差。

为了更加直观地描述实验结果，图3 展示了一组典型的直角壁面附近柱形空泡的高速摄影实验图像。空泡的具体位置为：l*= 3.84 和θ =30º。图中按照时间顺序展示了柱形空泡在第一周期溃灭过程中的若干典型高速摄影图像，每张子图所对应的序号和时间分别位于该图片的右上角和下方。在本文中，柱形泡出生时刻被定义为初始时刻t= 0 µs。图3(a)对应柱形空泡第一周期半径最大的时刻，图3(g)对应的是高速摄影机所能捕捉到的第一周期柱形空泡的最小半径时刻。另外，比例尺标注在图3(a)的左上角。可以看到，直角壁面附近的空泡在第一个振荡周期的绝大部分时间内（对应图3(a)～图3(f)），均有比较明显的深色轮廓，并且内部呈现出明亮通透的特征。这表明由于实验中设置的前后玻璃板间距h明显小于空泡能达到的最大直径，致使在此过程中空泡的前、后泡壁分别附着在前、后玻璃板上。因此，在这个时间段内可以将空泡近似看作高度保持不变的柱形。此外，在溃灭的中后期（对应图3(e)～图3(g)），远离直角壁面一侧的柱形空泡表面出现凹陷。随着空泡的溃缩，凹陷程度逐渐加深，液体射流逐渐形成并将柱形空泡分成两团（对应图3(h)）。随后，在第二周期中，两团空泡不断做方向相反的自旋运动，并不断向着壁面移动。此时空泡的柱形特征不再明显，并且空泡也相对混乱。因此，本文将着重分析柱形空泡在第一振荡周期中的特性。

图3 直角壁面附近柱形空泡的典型高速摄影图像（l* = 3.84，θ = 30º）Fig.3 Typical high-speed photographs of the cylindrical cavitation bubble near the right-angle wall (l* = 3.84, θ = 30º)

2 对称位置柱形空泡动力学行为分析

本节围绕柱形空泡的轮廓、柱形空泡在溃灭过程中圆度的变化情况以及形心移动距离的变化情况，对位于对称位置处的柱形空泡在径向上的各向异性运动特性以及平移特性进行分析。

图4～图6 分别展示了具有不同无量纲距离l*的直角壁面附近对称位置处典型柱形空泡高速摄影图像（如图4(a)，图5(a)，图6(a)所示）及其对应的空泡轮廓及形心位置随时间的变化（如图4(b)，图5(b)，图6(b)所示）。图4(a)，图5(a)，图6(a)展示了对称位置处柱形空泡溃灭阶段5 个典型时刻的高速摄影图像，其对应的比例尺均与图3 相同。在图4(b)，图5(b)，图6(b)中，相同时刻下空泡的轮廓和形心分别由具有相同颜色的虚线和符号点表示。可以看到，其中均包含与图4(a)，图5(a)，图6(a)对应的5 个典型时刻。具体来说，绿色对应于柱形空泡最大半径时刻（对应图4(a)，图5(a)，图6(a)的第一帧），而红、蓝、紫和黑色分别对应于柱形空泡在第一振荡周期溃灭过程中被高速摄影机捕捉到的最后4帧（对应图4(a)，图5(a)，图6(a)的2～5 帧）。除此之外，灰色代表直角壁面。从图4～图6 中均可以看出，当柱形空泡位于对称位置时，在空泡溃灭阶段内，靠近壁面顶点一侧的泡壁基本上不发生移动。而远离壁面顶点一侧的泡壁产生明显移动，并且逐渐形成指向壁面顶点方向的凹陷。此外，在溃灭过程中空泡的形心持续向直角壁面的顶点方向移动。但是，由于无量纲距离的不同，导致空泡在溃灭过程中的变形过程存在差异，空泡表面的凹陷出现的时间以及凹陷程度均有所不同。针对上述现象，可以进行如下解释。对称位置处柱形空泡周围液体压力分布不均匀，并且关于θ = 45°对称。同时，柱形空泡附近靠近壁面顶点一侧的压力较小，远离壁面顶点一侧的压力较大。这种压力的差异，呈现为指向壁面顶点的Bjerknes 力。在溃灭过程中，Bjerknes 力始终作用在空泡上，使得空泡的凹陷不断演化，形心位置不断移动。对于整个溃灭过程，可以用Bjerknes力在时间上的积分得到的Kelvin 冲量来分析柱形空泡的形态变化程度和移动的距离。当柱形空泡位于不同位置时，Bjerknes 力和Kelvin 冲量大小不同，从而导致柱形泡凹陷和移动的程度不同。

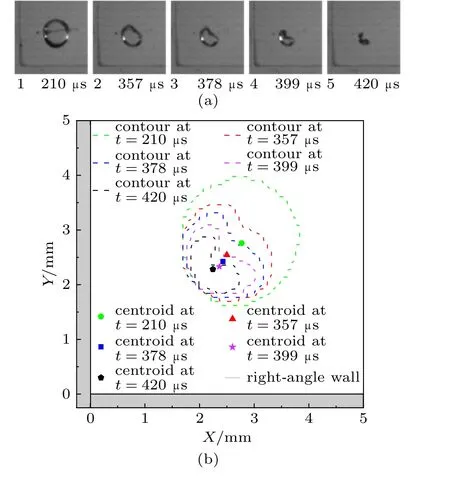
图4 （a）对称位置典型柱形空泡高速摄影图像及其（b）对应的空泡轮廓和形心位置（l* = 3.41，θ = 45º）Fig.4 (a) Typical high-speed photographs of the cylindrical cavitation bubble and (b) corresponding bubble contours and centroid positions in symmetrical position (l* = 3.41, θ = 45º)

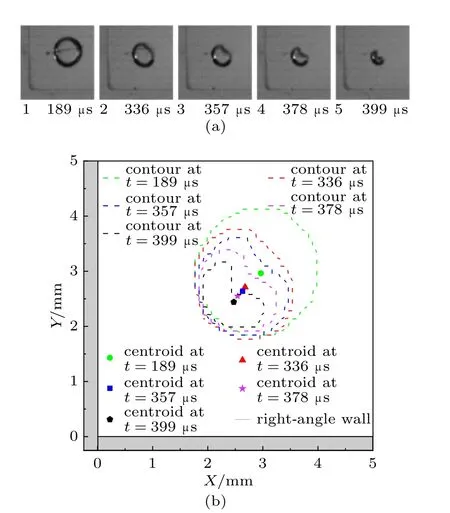
图5 （a）对称位置典型柱形空泡高速摄影图像及其（b）对应的空泡轮廓和形心位置（l* = 3.63，θ = 45º）Fig.5 (a) Typical high-speed photographs of the cylindrical cavitation bubble and (b) corresponding bubble contours and centroid positions in symmetrical position (l* = 3.63, θ = 45º)

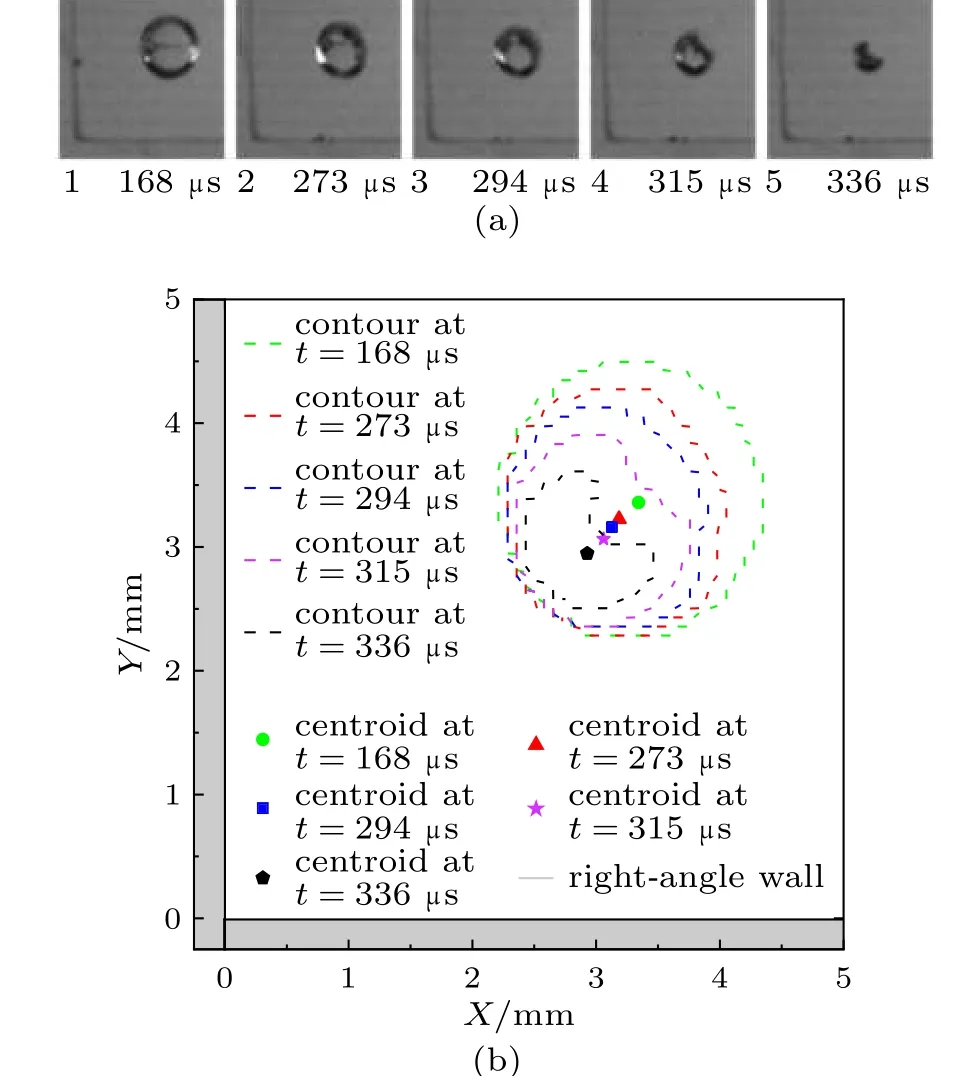
图6 （a）对称位置典型柱形空泡高速摄影图像及其（b）对应的空泡轮廓和形心位置（l* = 4.13，θ = 45º）Fig.6 (a) Typical high-speed photographs of the cylindrical cavitation bubble and (b) corresponding bubble contours and centroid positions in symmetrical position (l* = 4.13, θ = 45º)

在图4 状态，空泡与壁面顶点的无量纲距离较近，其l*= 3.41。可以发现，由于l*较小，空泡受到壁面的影响程度较大，因此空泡受到的Bjerknes 力和Kelvin 冲量较大，空泡表面的凹陷在溃灭中期就已出现（对应图中的红色虚线）。随着空泡的溃灭，该凹陷不断发展，在溃灭末期非常明显，且空泡整体呈现为比较扁的形状（对应图中的黑色虚线）。

在图5 状态，空泡与壁面顶点的无量纲距离居中，其l*= 3.63。此时，空泡受到的Bjerknes力和Kelvin 冲量大小相对适中。可以发现，在溃灭中期，空泡表面的右上方表现为较为平直（对应图中的红色和蓝色虚线）。与图4 相比，空泡表面的凹陷出现的时间更晚（对应图中的紫色虚线），且在溃灭末期凹陷的程度也更弱（对应图中的黑色虚线）。

在图6 状态，空泡与壁面顶点的无量纲距离较远，其l*= 4.13。可以发现，由于l*较大，空泡受到壁面的影响不明显，因此空泡受到的Bjerknes力和Kelvin 冲量较小，空泡在溃灭中期还能够保持准圆柱形（对应图中的红色和蓝色虚线）。与图4 和图5 相比，空泡表面的凹陷出现的时间最晚，且凹陷程度最弱。

此外，通过对比图4～图6 中空泡溃灭到最小体积对应的时间可以发现，随着l*的减小，空泡第一周期振荡的时间逐渐增长。也就是说，直角壁面对空泡的振荡周期具有一定的延长作用。

为了进一步定量分析柱形空泡在溃灭阶段的形态变化过程，引入圆形度e，其表达式为[13]

式中，S和L分别为被相机拍摄到的柱形空泡横截面的面积和周长。e的结果越接近于1，表示柱形空炮横截面越接近于圆形。

在此基础上，图7 展示了对称位置处具有不同无量纲距离的柱形空泡的圆度随时间的变化情况。在图7 中，红、绿和黄色数据点分别代表对称位置处无量纲距离l*= 3.41，3.63 和4.13 的情况，分别与图4～图6 相对应。图中t0表示柱形空泡最大半径对应的时刻。从图7 可以看出，对于不同的无量纲距离l*，在溃灭过程中柱形空泡的圆形度均越来越低，且减小的速度逐渐增大。这表示空泡在溃灭初期的变形程度较小，而在溃灭中后期各向异性变形的程度逐渐增大。此外，通过比较不同无量纲距离的情况可以发现，当无量纲距离较小时，空泡的变形受到直角壁面的影响最为强烈，空泡在溃灭末期的圆度可以达到较低的水平，约为0.60。而当无量纲距离较大时，空泡在溃灭末期的圆度维持在较高水平，约为0.77。

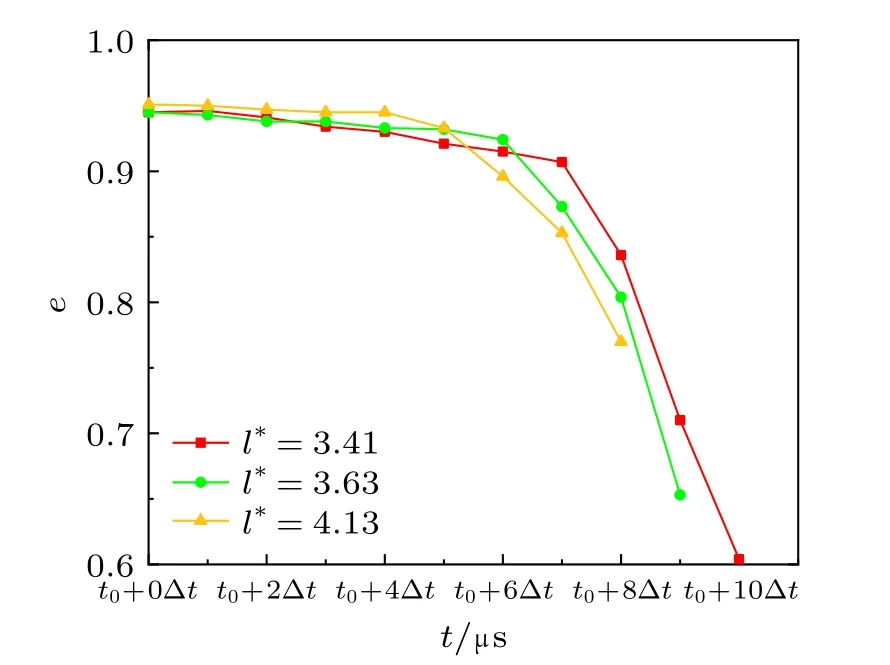
图7 柱形空泡在溃灭过程中的圆度随时间的变化（θ = 45º）Fig.7 Variations of the bubble circularity with the time during the collapse stage (θ = 45º)

图8 展示了对称位置处柱形空泡在溃灭过程中的形心移动距离随无量纲距离l*的变化情况。图中的dc表示柱形空泡在溃灭过程（即柱形空泡从第一周期最大半径至最小体积的过程）中的形心移动距离。如图8 所示，总的来说，随着无量纲距离l*的增加，柱形空泡形心移动距离逐渐减小。除此之外还可以发现，在无量纲距离较小的范围内（l*= 3.0～3.4），柱形空泡形心移动距离变化得更加剧烈；而无量纲距离较大的范围内（l*= 3.4～4.2），柱形空泡形心移动距离变化得相对平缓。这表明在同一个θ 的情况下，直角壁面对柱形空泡形心移动的影响随着无量纲距离的增加而减弱。

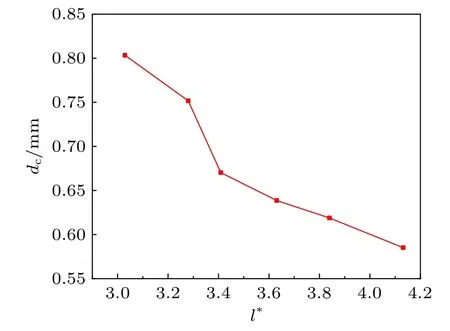
图8 柱形空泡在溃灭过程中的形心移动距离随无量纲距离l*的变化（θ = 45°）Fig.8 Variation of the bubble centroid movement distance with dimensionless distance l* during the collapse stage(θ = 45º)

3 非对称位置柱形空泡动力学行为分析

本节围绕柱形空泡的轮廓以及形心移动方向的变化情况，对位于非对称位置处的柱形空泡在溃灭过程中形态的非对称变化及空泡的平移特性进行分析。由于物理模型的对称性，本文只分析空泡位置角度θ < 45°的情况。

图9～图11 分别展示了具有不同空泡位置角度θ 的直角壁面附近非对称位置处典型柱形空泡的高速摄影图像及其对应的轮廓和形心位置随时间的变化。3 幅图中空泡与壁面之间的无量纲距离l*相同，均为3.41。图中各种颜色的虚线和符号点的含义与图4～图6 中的一致。从图9～图11中可以发现，在溃灭过程中空泡表面的右上部分仍然会形成凹陷并不断发展。但是，由于空泡位置的不对称性，在溃灭末期，空泡表面的凹陷在发展过程中会更偏向于左壁面。此外，由于空泡的右下部分比左上部分更加靠近壁面，泡壁的收缩速率更慢。上述两个因素相结合，导致空泡表面的凹陷不再将空泡的左上部分和右下部分平均分为等大的两部分。除此之外，柱形空泡在溃灭过程中的形心移动方向也不再指向直角壁面的顶点，而是偏向于空泡更加靠近的下壁面。但是，由于空泡位置角度的不同，空泡变形的非对称程度以及空泡形心移动的方向角度均存在差异。当柱形空泡处于非对称位置时，柱形空泡周围的液体压力分布不均匀且不再关于θ = 45°对称。总的来说，柱形空泡右上方远离壁面一侧的压力相对较大，但是此时柱形空泡靠近下壁面一侧和靠近左壁面一侧压力分布并不相同。相比较而言，柱形空泡靠近下壁面一侧压力比左壁面一侧更小，从而呈现出下壁面作用于柱形空泡的Bjerknes 力比左壁面更强，因此产生的Kelvin 冲量也会更加偏向下壁面。由于空泡位置角度的不同，因此直角壁面作用于柱形空泡的Bjerknes 力的方向也会不同，进而产生的Kelvin 冲量方向也不同。

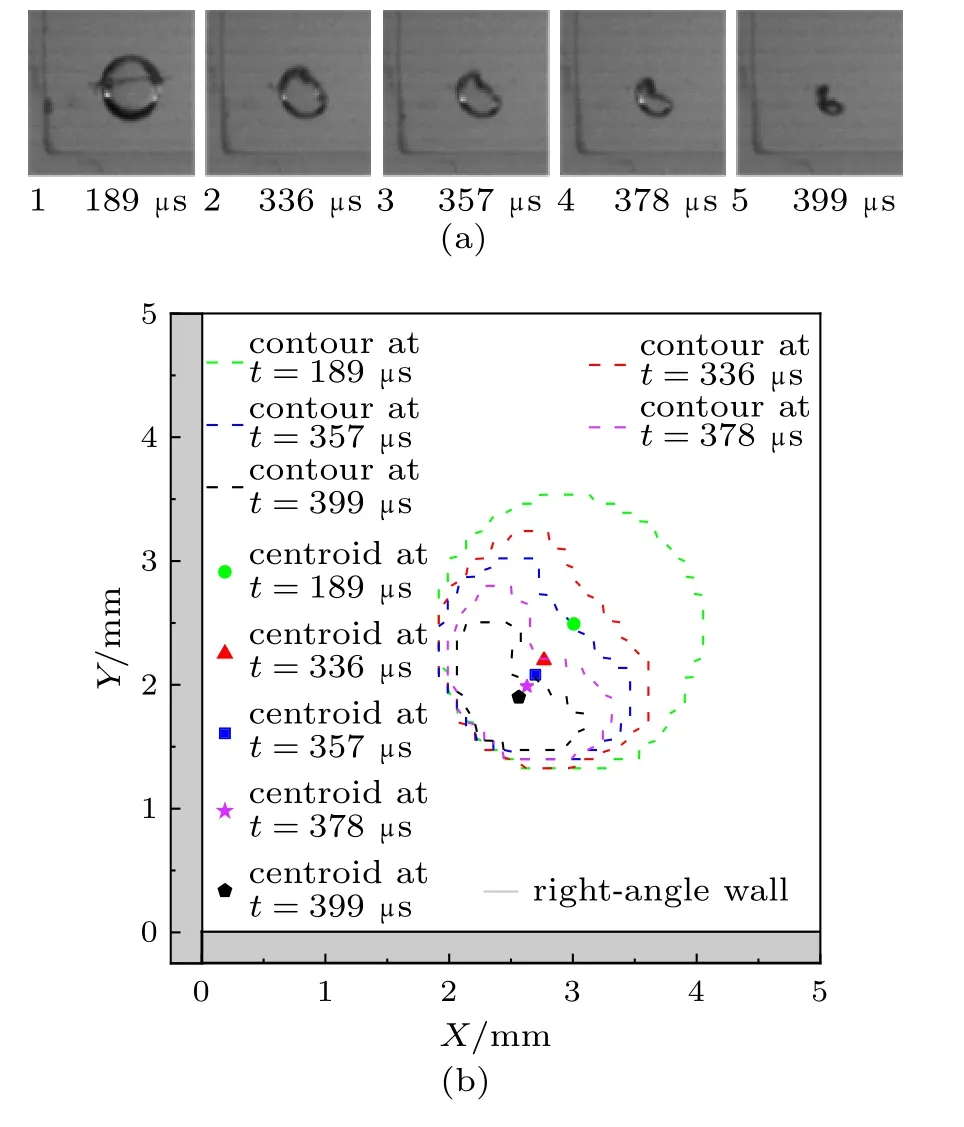
图9 （a）非对称位置典型柱形空泡高速摄影图像及其（b）对应的空泡轮廓和形心位置（l* = 3.41，θ = 40º）Fig.9 (a) Typical high-speed photographs of the cylindrical cavitation bubble and (b) corresponding bubble contours and centroid positions in asymmetric position (l* = 3.41, θ = 40º)

对图9 情况，空泡位置的非对称程度较低，其θ = 40°。此时，左壁面和下壁面作用于柱形空泡的Bjerknes 力差别不大，Kelvin 冲量方向偏向下壁面不明显。可以发现，在空泡的整个溃灭过程中，空泡的非对称变形程度以及空泡形心移动方向偏向下壁面的程度均不明显。

对图10 情况，空泡位置的非对称程度居中，其θ = 25°。此时，下壁面作用于柱形空泡的Bjerknes 力要稍大于左壁面，Kelvin 冲量方向也偏向下壁面。可以发现，在溃灭中后期，空泡表面右上方凹陷的形成位置几乎处于对称位置（对应图中的紫色虚线）。然而，在溃灭末期，空泡表面凹陷的发展方向逐渐偏向于左壁面，柱形空泡的形状不再对称（对应图中的黑色虚线）。空泡右下部分的体积明显大于左上部分。并且，与图9 相比，该情况下空泡与下壁面的距离更近，受到壁面的影响更大，空泡表面形成的凹陷程度也更大。此外，空泡形心的移动方向也更加偏向于下壁面。

图10 （a）非对称位置典型柱形空泡高速摄影图像及其（b）对应的空泡轮廓和形心位置（l* = 3.41，θ = 25º）Fig.10 (a) Typical high-speed photographs of the cylindrical cavitation bubble and (b) corresponding bubble contours and centroid positions in asymmetric position (l* = 3.41, θ = 25º)

对图11 情况，空泡位置的非对称程度较高，其θ = 20°。此时，下壁面作用于柱形空泡的Bjerknes 力要远大于左壁面，Kelvin 冲量方向更加偏向下壁面。与图9 和图10 相比可以发现，空泡右上方的凹陷出现较为明显的非对称特性的时间更加提前（对应图中的紫色虚线）。且在溃灭末期，空泡的左上部分与右下部分的体积差异更加明显。此外，在溃灭过程中的空泡形心移动方向更加偏向于下壁面。

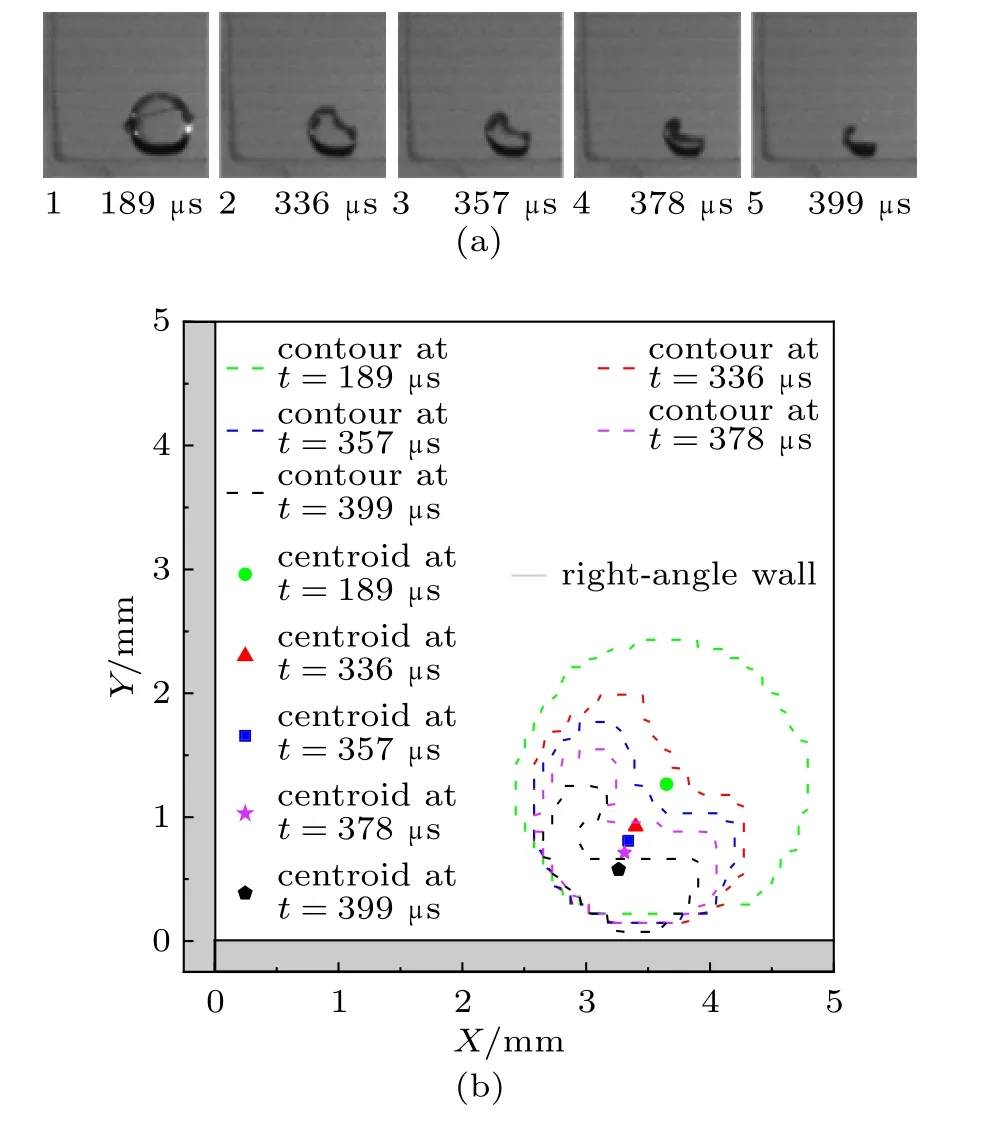
图11 （a）非对称位置典型柱形空泡高速摄影图像及其（b）对应的空泡轮廓和形心位置（l* = 3.41，θ = 20º）Fig.11 (a) Typical high-speed photographs of the cylindrical cavitation bubble and (b) corresponding bubble contours and centroid positions in asymmetric position (l* = 3.41, θ = 20º)

图12 展示了柱形空泡的形心在溃灭过程中的移动方向随位置角度的变化情况。在图12 中，柱形空泡与壁面顶点间的无量纲距离为l*= 3.41，与图9～图11 一致。由于直角壁面模型的结构是关于θ = 45°对称的，并且当位置角度θ 较小（θ小于15°）时，柱形空泡大部分时间与下壁面贴合，统计形心移动方向意义有限且较为困难，因此本文只讨论在θ 在 15°～45°的情况。如图12所示，随着柱形空泡位置角度θ 的增加，柱形空泡形心的移动方向角度θk逐渐增加，并且增加趋势逐渐趋于平缓。这表明在同一个l*情况下，随着柱形空泡逐渐靠近下壁面，下壁面的影响比左壁面更强而占主导作用，导致形心的移动方向由指向壁面顶点逐渐偏转为指向下壁面。

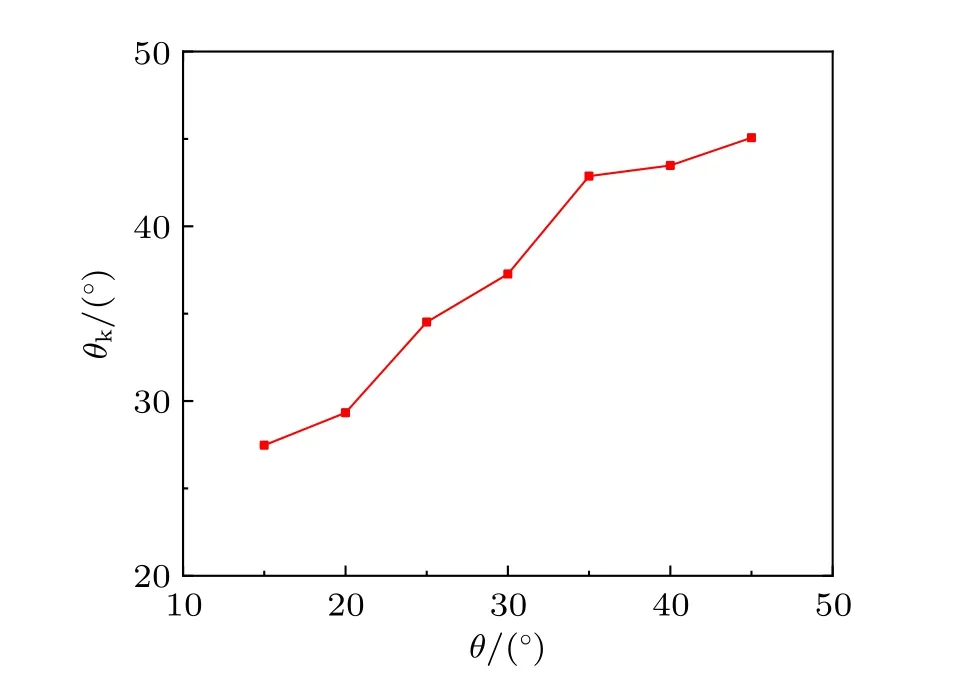
图12 柱形空泡溃灭过程形心移动方向随空泡位置角度θ的变化（l* = 3.41）Fig.12 Variation of the bubble centroid movement direction with bubble position angle during the collapse stage (l* = 3.41)

4 结论与展望

本文基于高速摄影实验，研究了直角壁面附近不同位置处的激光诱导柱形空泡的完整动力学过程。通过对对称位置和非对称位置的实验数据分别进行分析，揭示了直角壁面和柱形空泡的相对位置对柱形空泡泡壁变形、形心移动距离及移动方向等动力学行为的显著影响。本文的主要结论如下。

（1）直角壁面附近的柱形空泡在第一周期溃灭阶段内，靠近壁面或者直角壁面顶点一侧的泡壁向内收缩的速率很小，而远离壁面一侧的泡壁会出现凹陷，并且逐渐发展直至将柱形空泡分为两部分。

（2）当空泡位于对称位置时，随着空泡与直角壁面之间无量纲距离l*的逐渐增大，直角壁面对柱形空泡的影响越来越弱，柱形空泡表面凹陷形成的时间越晚，且溃灭末期的凹陷程度越弱。此外，柱形空泡在溃灭阶段的形心移动距离也逐渐减小。

（3）当空泡位于非对称位置时，随着空泡位置角度θ 的逐渐减小（对θ < 45°的情况而言），空泡表面凹陷的发展方向会逐渐偏向于左壁面，空泡右下部分的体积会逐渐大于左上部分。此外，由于下壁面的影响逐渐占据主导，柱形空泡形心的移动方向由指向壁面顶点逐渐变为指向下壁面。

在后续的工作中，通过改变两玻璃板间隙的宽度以及角形壁面模型的形状，将进一步探究柱形泡的高度以及壁面夹角等参数对柱形泡动力学行为的影响。