基于熵产的肘形吸入流道对管道泵性能的影响分析

吴宏飞，姜永明，赵才甫，温庆斌，郭 英

（南方泵业股份有限公司，杭州 311107）

0 引言

管道泵多为单级单吸式离心泵，具有结构简单，便于安装和维修等优势，主要作为液体输送、增压和循环设备使用［1］。在实际工程中，为适应管路安装，管道泵多采用肘形吸入流道。同时，为了减少生产和设计成本，其叶轮和压出室往往会直接采用与直锥形端吸泵相同结构的水力设计。然而，在同一工况下，管道泵相比于端吸泵会出现效率降低的现象，并且大流量下更容易产生汽蚀和振动等问题。相关研究表明，肘形吸入流道的弯角和曲率等参数是影响管道泵水力效率的关键［2］，但对其流动损失的分布特性和影响机理尚缺乏深入研究。传统的管道泵吸入流道的水力设计大多参考现有的优秀模型，并结合计算流体力学（CFD）仿真技术进行优化设计，但是基于压力场及速度场的分析结果无法展现不良流动的动力学根源。

熵产理论作为一种直观反映流体过程中不可逆损失发生位置及能耗空间分布的有效工具，为离心泵性能改进及优化提供了新的思路。相较于传统的水力损失评估方法，基于熵产理论的分析方法的优势在于能够准确地预测离心泵内能量损失的具体区域，为研究人员开展针对性的流动不稳定分析、优化设计及主动控制提供准确直观的参考信息［3-10］。冯建军等［11］利用熵产理论获得了离心泵事故断电停机飞逸过程中过流部件流场能量损失分布情况，并对流场内随时间变化的能量损失进行定量评估。潘强等［12］通过熵产理论定位贯流泵内能量损失较高的局部区域，分析了不同工况下各部件内局部熵产、能量损失和不稳定流动之间的关联。卢金玲等［13］采用熵产理论对水轮机尾水管内的涡带特征及压力脉动特性进行了研究，发现水轮机的叶片压力面的流动分离是熵产产生的主要原因，涡带的产生使得尾水管区域出现高熵产率的带状区域。张永学等［14］将局部熵产理论引入离心水泵的损失计算，对离心泵内的能量损失特性进行了系统评估，发现离心泵蜗壳和叶轮是熵产发生的主要区域，且湍流熵产与壁面熵产占比较大。黄宁等［15］将熵产分析理论，应用于流场的后处理，对液力透平导叶及转轮流场进行分析。吕剑渊等［16］利用熵产理论和Q准则等方法，研究了不同角度的蜗壳隔舌安放角，得出适当地增大蜗壳隔舌安放角可以降低离心泵的机械能损失，提高离心泵能量的利用，减小蜗壳隔舌处的回流以及降低压力脉动。舒欣等［17-21］采用熵产理论和Q准则对不同转速和工况下的自吸泵内部各个部件的流动损失特性进行定量分析，得到腔体、蜗壳和叶轮是离心泵内部能量损失的核心区。柴博等［22-25］众多学者也采用不同方法对离心泵不同特性进行了大量分析研究，同时也取得了一定进展。

目前，将熵产理论应用于流体机械内部流动损失分析已经较为成熟，但是基于熵产理论开展管道泵的研究尚少且未形成系统性研究。本文引入熵产理论，从流动机理和能量损失等方面，开展了管道泵内部流动损失的定量研究，对比直锥形吸入流道，分析了肘形吸入流道对管道泵内部损失特性的影响机理。

1 物理模型及计算方法

1.1 计算模型

以比转数为190的管道泵为研究对象，其设计参数为：流量Q=400 m3/h，扬程H=20 m，转速n=1 450 r/min。在主要几何参数中，叶轮进口直径D1=200 mm，叶轮外径D2=278 mm，叶轮出口宽度b2=48 mm，叶片数Z=7，蜗壳基圆D3=288 mm。分别对管道泵和端吸泵建立三维计算域模型，如图1所示。

图1 流体计算域Fig.1 Computational domains of fluid

数值计算区域由吸入流道，叶轮水体，蜗壳水体3个部分组成，其中对吸入流道及蜗壳出口段进行相应的延伸。

1.2 网格划分及计算方法

各部分计算域均采用结构化六面体网格划分，同时对叶片、叶轮和蜗壳交界处、隔舌等部位进行局部加密，其中叶轮处的网格划分如图2所示。选取流体域网格总数为377万，网格质量均大于0.4，满足计算要求。采用ANSYS CFX软件对管道泵的内部流动进行数值模拟，其中湍流模型采用了标准k-e模型；边界条件采用总压进口及质量流量出口，设置叶轮水体为旋转域，其他部件为静止域，动静交界面设置为冻结转子，壁面为无滑移壁面；流体介质为25 ℃水；以最大残差小于10-4作为计算收敛的唯一标准。

图2 叶轮网格划分Fig.2 Mesh generation of impeller

1.3 熵产计算方程

离心泵在运行过程中由于输送介质的黏性及雷诺应力的存在使得机械能不可逆地向内能转化，引起熵产的增加。对于湍流运动，熵产率可分为2个部分：（1）由时均速度引起的直接耗散熵产率Spro，VD；（2）由湍流脉动速度引起的湍流耗散熵产率Spro，TD。其具体表达式［18］如下：

式中，μ为动力黏度；T为流体质点温度；u，v，w分别为质点速度在X，Y，Z方向上的分量。

直接耗散熵产率S可以通过数值计算得出，湍流耗散熵产率可根据KOCK等［19］和MATHIEU等［20］提出的方法计算，其具体表达式如下：

式中，ρ为密度，kg/m3；ε为湍流耗散率，m2/s3；T为介质温度，K。

通过体积分可得到直接耗散熵产和湍流耗散熵产，即：

熵产率存在较强的壁面效应，张翔等［21］给出了壁面附近熵产计算公式：

式中，A为面积，m2；τ为壁面切应力，Pa；v为近壁面速度，m/s。

整个系统计算域内的总熵产Spro为直接耗散熵产SVD、湍流耗散熵产STD和壁面熵产Spro，W之和，即：

2 试验装置及试验方案

在闭式试验台进行泵性能的测试，该试验台符合GB/T 3216—2016《回转动力泵水力性能验收试验1级、2级和3级》和GB/T 12785-2014《潜水电泵试验方法》1级精度要求，并通过CMA与CNAS 认证。

试验中所采用的仪器仪表精度等级情况为：电磁流量计0.5级，压力变送器0.2级，电参数仪0.2级，仪器仪表均在检定有效期内。

3 结果讨论及分析

3.1 试验结果验证

基于闭式试验台开展了0.5Q～1.2Q流量工况下管道泵和端吸泵的水力性能试验，由于数值模拟直接得到的效率为水力效率，故对其进行换算后再与实测数据进行对比，得到二者的效率曲线如图3所示。结果表明，数值模拟与实测效率曲线的变化趋势基本保持一致，二者的结果偏差在3%左右，数值模拟精度满足后续计算分析要求。

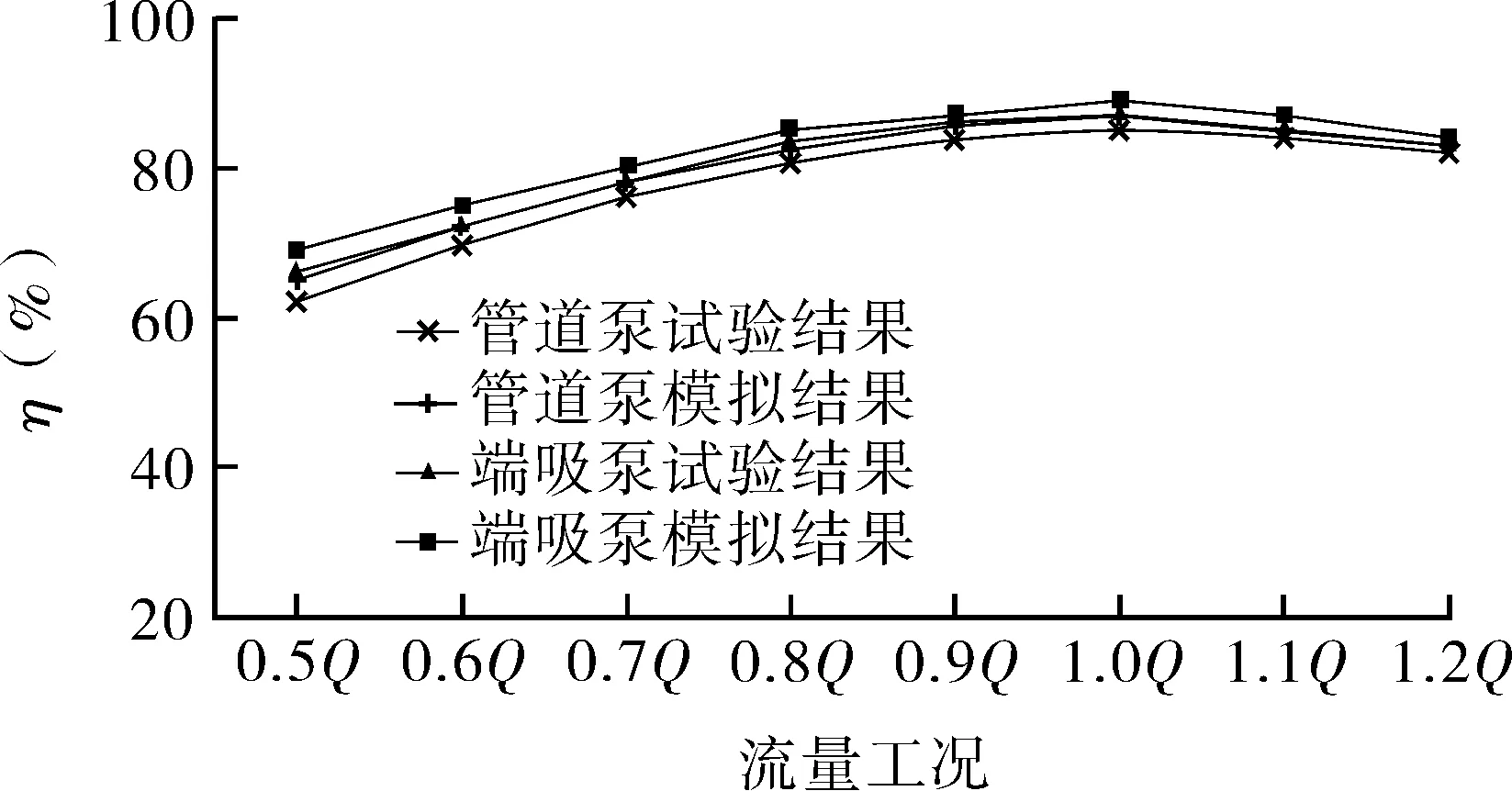
图3 外特性曲线Fig.3 External characteristic curve

3.2 能量损失分析

3.2.1 熵产结果可靠性验证

为了分析泵内流动损失分布特性，通过数值计算获取了不同工况下泵内部总损失ht［17］，其计算式如下：

式中，hs为吸入段的水力损失，m；hi为叶轮的水力损失，m；hv为蜗壳的水力损失，m。

为验证熵产理论计算水力损失的正确性，将各个流体单元的水力损失与熵产得到的水力损失进行了对比，图4（a）（b）分别示出了不同流量工况下泵内各部分的水力损失和熵产分布。

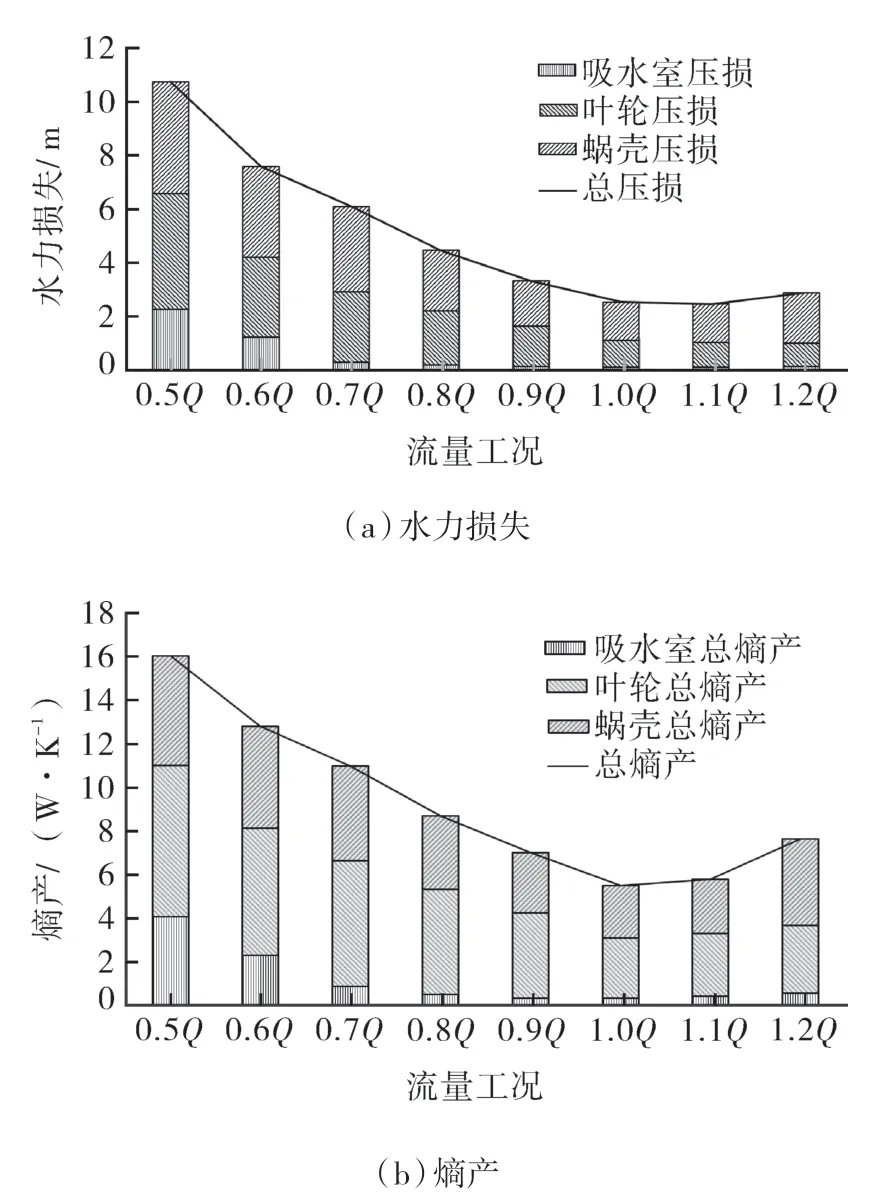
图4 泵内能量损失分布规律Fig.4 Distribution law of energy loss in the pump

结果显示，在不同流量下，2种方法计算得到的水力损失及变化趋势相近。随着流量的增加，水力损失先减小后增加。在额定工况下，水力损失最小，在小流量下总水力损失显著增加，且吸入流道的水力损失增加较为明显。从总体上看，各工况下2种方法得出的水力损失最大误差在5%左右，说明熵产理论用于开展不可逆损失的定量分析较为可靠。

3.2.2 吸入流道形状对泵内流动损失的影响

图5示出了管道泵吸入流道改型前、后的熵产分布规律。

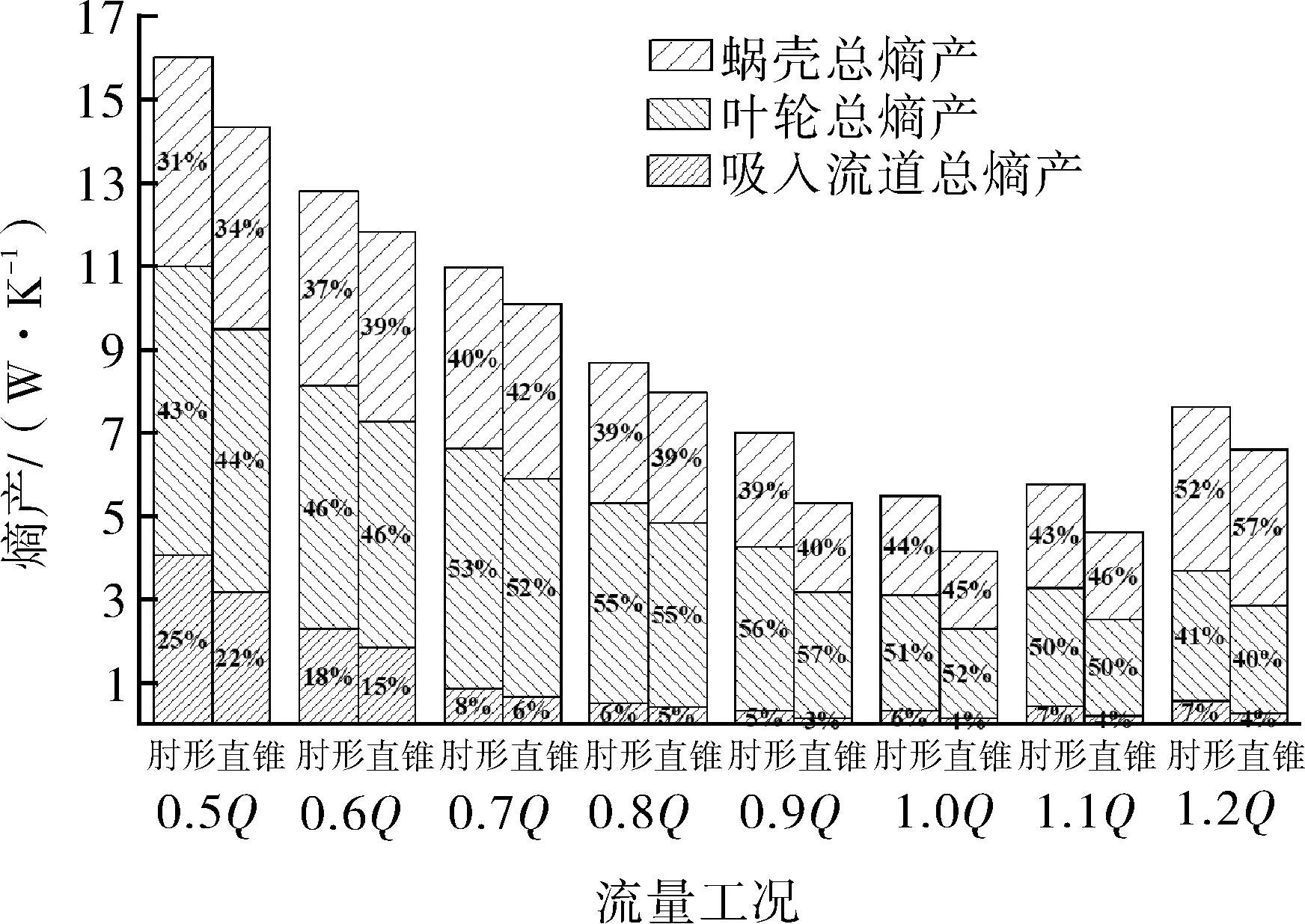
图5 总熵产分布规律Fig.5 Distribution law of the total entropy production

首先，吸入流道的改型并未改变熵产随流量变化的趋势，肘形吸入流道与直锥形吸入流道泵内熵产值均随着偏离额定工况逐渐增大。总熵产主要由叶轮和压出室（蜗壳）熵产组成，吸入流道的熵产随着流量减小逐渐增大。从熵产值来看，在不同流量工况（0.5Q～1.2Q）下，肘形吸入流道熵产均大于直锥形吸入流道熵产，管道泵总熵产均大于端吸泵总熵产。结果表明，吸入流道的改型并未影响管道泵整体性能曲线的走向，但从定量上来看，改用肘形吸入流道使得相同工况下的总水力损失增加，这与试验测量得到的管道泵效率低于端吸泵效率的结论相符（见图3）。

为进一步研究各过流部件的水力损失来源，将总熵产分为直接熵产、湍流熵产和壁面熵产3个部分，图6示出了各过流部件的熵产分布特征。结果显示，各过流部件的熵产主要由湍流熵产和壁面熵产组成，直接熵产较小，约为总熵产的1%。在额定工况下，泵内湍流熵产和壁面熵产最小，且随着流量的增大或减小，湍流熵产和壁面熵产均增大。由图6（a）肘形与直锥形吸入流道熵产分布可知，在额定工况Q下，湍流熵产约占吸入流道总熵产47%，壁面熵产约占吸入流道总熵产53%。随着流量减小，吸入流道总熵产迅速增加，在0.5Q的工况下，湍流熵产占比达到80%左右。由图6（b）叶轮熵产分布可知，在额定工况下，湍流熵产约占叶轮总熵产50%，随着流量的减小，叶轮总熵产迅速增加，在小流量工况下，湍流熵产约占叶轮总熵产90%。由图6（c）蜗壳熵产分布可知，额定工况附近，湍流熵产和壁面熵产相近；在0.5Q工况下，湍流熵产约占78%；在1.2Q工况下，湍流熵产约占55%。

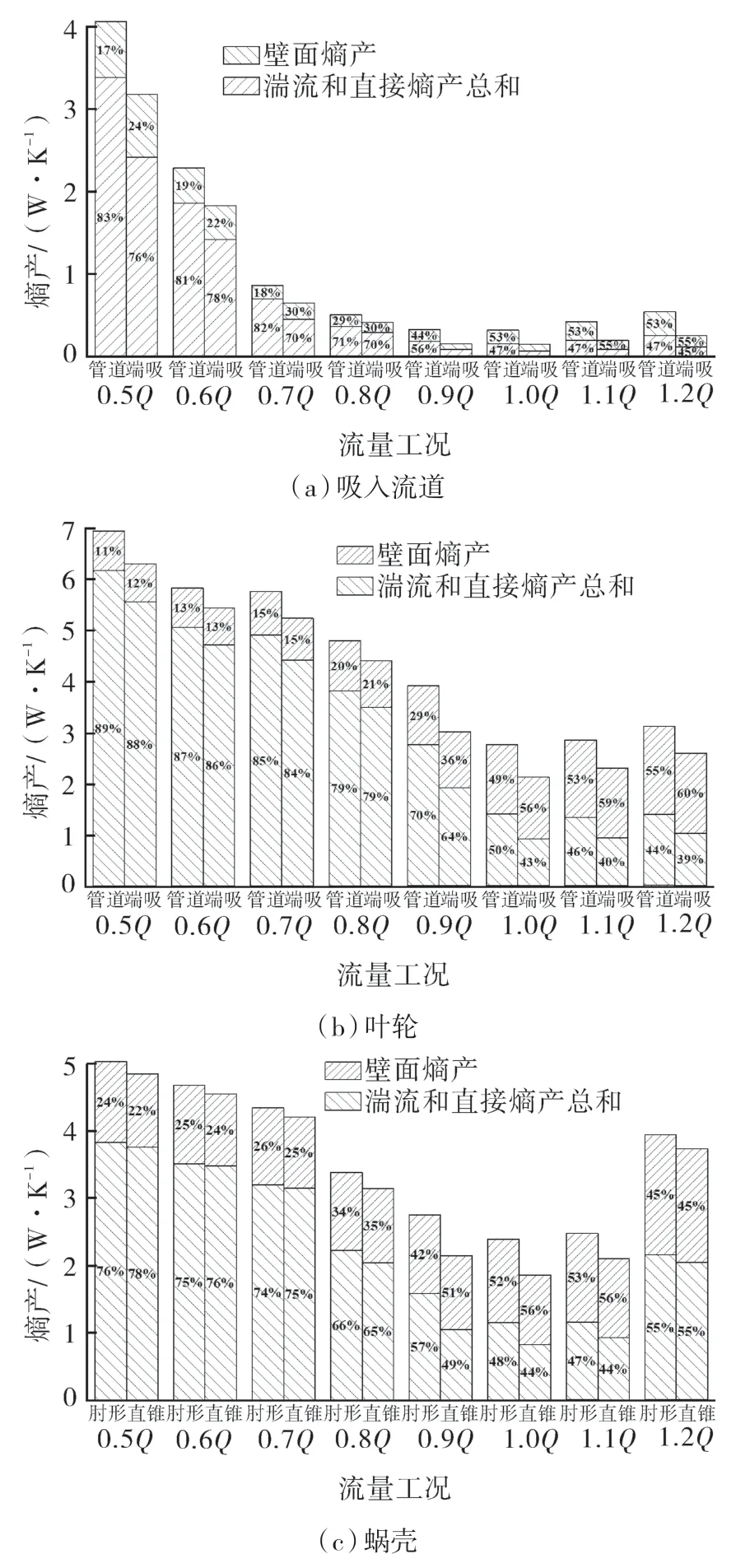
图6 泵内部熵产分布及占比Fig.6 Distribution and proportion of entropy production in the pump

结果表明，管道泵内部水力损失主要来源于湍流脉动以及壁面流体黏性引起的能量耗散，而流体的时均运动所产生的水力损失几乎可以忽略。随着偏离额定工况，流动脉动增强，因此而引起的水力损失成为了总损失的主要来源。对比直锥形吸入流道，改用肘形吸入流道主要增加了各过流部件中的湍流脉动。

3.2.3 泵内部流动特征分析

为了研究吸入流道对离心泵内部流动损失的影响机理，将通过分析各部件内部流动、熵产率分布及涡量变化等泵内流动特征进一步讨论吸入流道对过流部件的影响。

将叶片进口边旋转1周得到过水断面，如图7所示，此过水断面上的速度分布可视为叶片进口处的速度分布。选取额定工况Q，小流量工况0.6Q及大流量工况1.2Q作为分析对象。

图7 过水断面示意Fig.7 Schematic diagram of crossing section

图8示出3个工况下管道泵与端吸泵的叶片进口速度分布云图，可以看出，在各个工况下，管道泵叶片进口过流断面速度分布与端吸泵相比对称性较差，说明流动更加紊乱，加剧了水力损失。

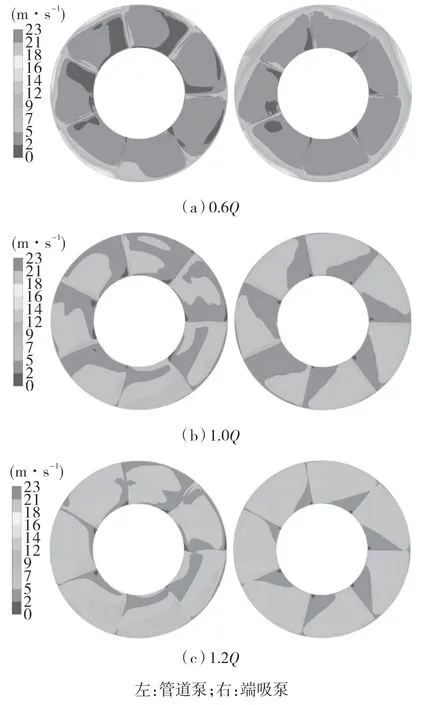
图8 不同工况叶片进口速度分布Fig.8 Distribution of blade inlet velocity under different flow rates

图9示出了3个工况下叶轮50%叶片高度处的局部熵产率分布特征。

在各个工况下，管道泵和端吸泵叶轮流体域中间流面熵产率分布并不相同且损失主要集中在叶片进口处。在额定流量工况（1.0Q）下，端吸泵在叶轮内部的熵产率较小，这是由于此时叶片进口角接近相对液流角，冲击损失较小。相比较而言，管道泵的叶片进口处的熵产率较大且不均匀。结合叶片进口处的流场特征（见图8），液流在经过肘形吸入流道进入叶轮时速度分布不均匀，进而在叶片进口处产生冲击，并影响了叶片间的流动，造成效率下降。在大流量工况（1.2Q）下，端吸泵叶轮和管道泵叶轮的熵产率分布与额定工况相近。主要是由于在叶轮设计之初考虑到大流量工况，因此叶片进口角增加了冲角来改善大流量下的性能。在小流量工况（0.6Q）下，端吸泵叶轮和管道泵叶轮均在大面积范围内呈现高熵产率，且主要位于叶片前缘和非工作面前端区域，其原因是小流量工况下液流以小于叶片进口安放角的角度冲击叶片的工作面，在叶片工作面产生脱流，该处是叶道的高压侧，形成的漩涡会向低压侧扩散，产生较大湍流耗散，这就使得在0.6Q工况下的高熵产率分布范围更大。另外，与大流量工况类似，相比于端吸泵，管道泵叶轮高熵产率分布不均匀性更强，且分布范围更广。

总之，吸入流道的改型使得管道泵各部件内部熵产率更高且分布更广。肘形的设计使得流体在吸入流道突然转弯，影响了叶轮入口处的流动均匀性，使得各过流部件内部流动偏离最优工况，不良流动（脉动及漩涡等）增加，甚至可能诱导流动分离或二次流的提前发生。

4 结论

（1）随着偏离设计流量工况，管道泵整体水力损失逐渐增大，吸入流道的改型并未改变不同流量工况下总体流动损失的变化趋势。总熵产主要由叶轮和压出室（蜗壳）熵产组成，而吸入流道的熵产占比最小。

（2）管道泵内各流体单元熵产主要由湍流熵产和壁面熵产组成，其中直接熵产占比较小（约为1%）。相比于直锥形吸入流道，肘形吸入流道主要增强了流动的湍流脉动，增加了湍流熵产，加剧了整体水力损失。在小流量工况（0.5Q）下，湍流熵产可达到叶轮处总熵产的90%左右。

（3）管道泵叶片进口过流断面速度分布与端吸泵相比对称性较差，各流体单元的高熵产区域更广。叶轮入口的流动不对称性增强了叶轮出口动静干涉作用，使得流动分离和回流增加，叶轮熵产率显著增加，且加剧了整体流动损失。