含有偏置电压源的非齐次分数阶忆阻混沌电路动力学分析与实验研究*

吴朝俊 方礼熠† 杨宁宁

1) (西安工程大学电子信息学院,西安市电气设备互联感知与智能诊断重点实验室,西安 710048)

2) (西安理工大学电气工程学院,西安 710048)

1 引言

忆阻器是蔡绍棠[1,2]提出的第4 种基本电路元件,由于其独特的非易失性和非线性,在神经网络、人工智能、数据存储和混沌电路等领域中得到了广泛关注和深入研究[3–8].众所周知,非线性元件,例如蔡氏二极管和忆阻器等[9,10],对混沌系统复杂动力学行为的产生起着重要的作用.因此,在过去的十多年中,研究者提出了众多包含不同非线性函数的忆阻器[11–14].由于蔡氏电路、文氏桥振荡器和Shinriki 振荡器等都只涉及结构对称的非线性系统,因此它们能产生对称的双涡卷吸引子[15–17].目前,学者们试图将具有不对称电压-电流(V-I)特性的非线性元件引入到一些现有的振荡电路中,以探索结构上的不对称效应[18,19].Cao 等[20]提出了一种具有非对称结构的混沌Jerk 电路,在此基础上得到了非对称双涡卷吸引子和非对称的共存分岔模式.Kengne 等[21]提出了将不对称二极管桥忆阻器引入混沌电路的模型,该模型产生了多种动力学行为,包括周期、混沌、周期泡、混沌泡、倍周期分岔等现象.此外,Wu 等[22]提出了在二极管桥中插入偏置电压源的模型,并将其引入Shinriki 振荡器中.由于偏置电压源的引入,使系统的不对称性具有连续可调的特点,使原来对称的吸引子逐渐转变为不对称的吸引子.

由于纳米级器件的制作成本和实现难度,目前对忆阻器的研究大都停留在实验室层面.通过开发具有忆阻器特性的等效电路,可以使忆阻器得到更加普遍的研究,拓宽忆阻器的研究领域,对其发展和应用具有促进作用.同时,研究表明电容、电感等器件是分数阶的,分数阶模型比整数阶模型更精确.建立非理想忆阻器的分数阶模型,可以获得更加接近实际的特性[23].目前对于含有偏置电压源的忆阻器的研究还停留在整数阶,而由于其具有不对称紧磁滞回线的调控能力,使获得物理忆阻器的不对称紧磁滞回线更容易.且分数阶微积分对模型的描述更加接近其本质特征,在将含有偏置电压源的忆阻器推至分数阶后,可以获得更加精确的忆阻器模型,同时系统的阶次也会对动力学行为产生影响.

为了研究含有偏置电压源的分数阶忆阻器的电路特性,本文首先建立了一种含有偏置电压源的分数阶二级管桥忆阻器模型,并对其电气特性进行了分析.其次,将此模型引入到Jerk 振荡器中,并将电路模型中的电容元件推广到分数阶次,建立了含有偏置电压源的分数阶非齐次忆阻混沌电路模型.研究偏置电压源电压改变对系统动力学行为的影响,结果表明在分数阶系统中引入电压偏移量,当初值为正时,系统随偏移电压的增大逐渐由周期态进入混沌态,当初值为负时系统并不受偏移电压的影响.再次,在PSpice 中搭建了分数阶非齐次忆阻混沌电路的等效电路模型,完成了整数阶与分数阶的电路仿真.最后,在NI 设备上进行了系统的电路实验,进一步证明了理论分析的正确性与可行性.

2 分数阶微积分理论概述

式中,q为分数阶微积分的阶次,t为自变量,m表示该变量的下边界,τ表示时间变量.

分数阶微分算子普遍接受的定义主要包括GL,R-L 和Caputo 定义.与其他定义下的分数阶微分算子相比,Caputo 分数阶导数定义具有与整数阶微积分相同的形式,对该类型分数阶导数采用Laplace 变换更清晰,并在诸多实际应用问题处理中得到广泛使用.因此,本文采用Caputo 定义的微分算子.Caputo 分数阶导数定义如下:

式中,f(t)是关于时间t的连续性函数;n∈N,是不小于q的最小整数;Γ(·) 为Gamma 函数,其表达式为

在理想条件下,当q无限接近于n时,Caputo导数也就成了函数f(t) 的常规n阶导 数.Caputo分数阶导数的Laplace 变化为

式中,s表示复频率,k表示正整数变量.

因为本文只涉及系统初值为零时的情况,所以Caputo 分数阶导数的Laplace 变换能够化简为以下形式:

3 含有偏置电压源的分数阶忆阻器与混沌电路建模

3.1 含有偏置电压源的分数阶二极管桥忆阻器建模

Wu 等[22]提出了一种在二极管桥忆阻器中串联一个电压源的模型,可以通过调整串联电压源Em的幅值来控制忆阻器紧磁滞回线的对称性,电路结构简单如图1 所示.该忆阻器电路由4 个二极管、1 个电阻、1 个电容以及1 个直流电压源构成.

图1 含偏置电压源忆阻器等效电路及忆阻器符号[22]Fig.1.Equivalent circuit of memristor with bias voltage source and symbol of me mristor[22].

研究表明实际的电容与电感等非线性元件都表现出分数阶特性,所以本文在图1 含有偏置电压源的忆阻器的基础上,将电容拓展到分数阶次,构成了一种新型的含有偏置电压源的分数阶忆阻器.其电路等效模型如图2 所示.

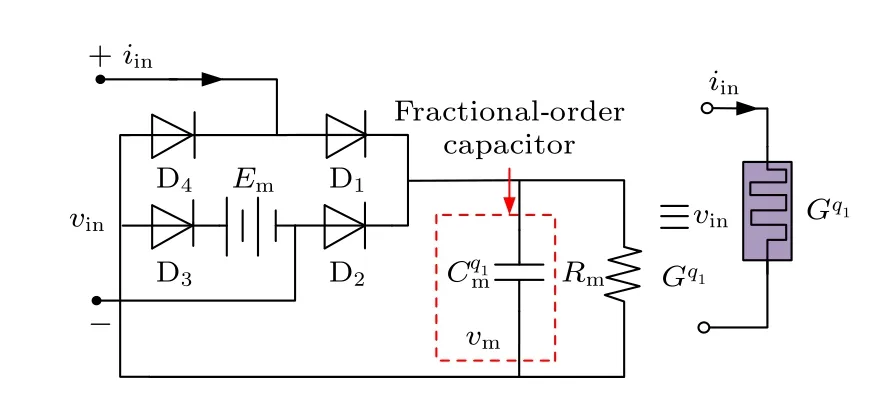
图2 含偏置电压源的分数阶忆阻器等效电路及忆阻器符号Fig.2.Equivalent circuit of fractional memristor with bias voltage source and symbol of memristor.

对于图2 中的分数阶忆阻器电路模型,结合基尔霍夫定律,电路方程可以表示为

式中,ξ=1/(2nVT),IS,n和VT分别表示二极管的反向饱和电流、发射系数和热电压.vm为电容两端电压,iin为分数阶忆阻器的端口电流.所采用的二极管参数为IS=2.682 nA,n=1.9,VT=26 mV.

根据上面建立的电路模型,通过Matlab 软件进行数值仿真,研究分数阶忆阻器的电气特性.给定一个正弦激励信号vin=Asin(2πft),并将分数阶电容值设置为5.8 μF,电阻值为Rm=1 kΩ.当输入信号的幅值A=2 V,偏置电压源Em=0 V,分数阶电容阶次q1=0.98 时,改变频率,得到的含偏置电压源的分数阶忆阻器的磁滞回线如图3(a)所示.分数阶忆阻器的vin-iin曲线是通过原点收缩的紧磁滞回线,并且随着频率的增大,紧磁滞回线包围的面积逐渐收缩.当改变其阶次(其他参数不变),得到的磁滞回线如图3(b)所示.在相同参数下,随着分数阶阶次的增大,紧磁滞回线包围的旁瓣面积会逐渐变小.最后,图3(c)为其他参数不变,在不同偏置电压下的磁滞回线,随着偏置电源电压Em的增大,磁滞回线的不对称性明显变强.

图3 含偏置电压源的分数阶忆阻器磁滞回线 (a) q1=0.98,Em=0 V,频率改变;(b) f=200 Hz,Em=0.1 V,分数阶次改变;(c) q1=0.98,f=200 Hz,偏置电压改变Fig.3.Hysteresis loop of fractional memristor with bias voltage source: (a) q1=0.98,Em=0 V,frequency change;(b) f=200 Hz,Em=0.1 V,fractional order change;(c) q1=0.98,f=200 Hz,bias voltage change.

由图3 可以看出分数阶忆阻器的左右旁瓣面积的对称性被打破,V-I曲线的不对称程度可以由电压源Em的值来控制,将V-I曲线的不对称度δ定义为电流iin的谷底值与峰值的比率,表示为

δ值域在[0,1]中.当f=500 Hz,q1=0.98,Em=[0 V,1 V],δ相对于电压源Em的演变曲线在图4中给出.对于Em=0 V 的对称分数阶二极管桥忆阻器,δ=1.随着Em的增大,分数阶二极管桥忆阻器的不对称程度增大,相应的不对称度δ逐渐减小.当Em变为约0.5 V 时,δ接近0,导致旁瓣的右叶消失.如上所述,当Em>0 V 时,分数阶二极管桥忆阻器是不对称忆阻器.分数阶二极管桥忆阻器的不对称程度可以通过电压源Em连续调整,适合于电路应用.

图4 V-I 曲线的不对称程度Fig.4.Degree of asymmetry of the V-I curve.

3.2 非齐次分数阶忆阻混沌电路建模

通过将Jerk 混沌振荡电路与含偏置电压源的分数阶忆阻器相结合,并将Jerk 混沌电路中的一个电容元件改为与分数阶忆阻器不同的阶次,组合成一种新型的含偏置电压源的非齐次分数阶忆阻混沌电路.图5 给出了其电路原理图,据此系统的电路模型为

图5 非齐次分数阶忆阻混沌系统Fig.5.Non homogeneous fractional order memristor chaotic system.

式中,电压v1和v3分别表示电容C1和C3两端的电压,v2为分数阶电容两端的电压,vm为分数阶忆阻器中分数阶电容两端的电压.元件参数取值如下:Ra=0.9524 kΩ,Rb=3.846 kΩ,Rc=15 kΩ,R1=R2=R3=R4=R5=R6=10 kΩ,Rm=1 kΩ,C1=C3=10 nF,=10 nF,=5.8 μF.

将时间、参数以及变量进行重新标度,取值如下:Vref=2nVT,t=R1C1τ,x1=v1/Vref,x2=v2/Vref,x3=v3/Vref,x4=vm/Vref,a=R/Ra,b=R/Rb,c=R/Rc,d=Em/Vref,ξ=1/(2nVT),ε=(R1IS)/Vref,β=C1/Cm,γ=R1/Rm.可以得到系统的无量纲方程如下:

4 混沌系统动力学行为分析及电路仿真

4.1 系统稳定性分析

4.1.1 整数阶系统

先对整数阶系统的稳定性进行分析.将(9)式左侧各项设置为0,通过化简整理后,方程组变为如下的形式:

将(10)式中的其他电路参数固定,使之随着参数d变化,通过Matlab 为两个超越方程绘制两条隐函数曲线,并通过检查这两条曲线的交点获得解集,(10)式的每个解对应一个平衡点.图6 给出了d=0,0.1,0.3 的曲线,当d变化时,对于每个参数d的值,系统始终存在3 个平衡点P-,P0和P+.且随着参数d增大,平衡点P-与P0的位置始终不变,而P+的位置沿右上方向逐渐偏离原点.平衡点P处的系统模型(10)的雅可比矩阵MJ推导如下:

图6 参数d 变化的平衡点在x1-x4 平面上的分布Fig.6.Distribution of equilibrium points for parameter d changes on the x1-x4 plane.

平衡点P的稳定性可以基于计算的特征值来确定,使用Matlab 计算(11)式给出的雅可比矩阵特征值,所得结果如表1 所列.P0是一个不稳定的指数1 鞍焦点(USF),由一个正实根、一对具有负实部的复根和一个负实根组成,而P-和P+是两个不稳定的指数2 鞍焦点,具有一对具有正实部的复根和两个负实根.对于所有参数d,P-和P0处的特征值保持不变,而P+处的特征值明显变化.

表1 系统平衡点及其稳定性Table 1.System equilibrium point and its stability.

4.1.2 分数阶系统

引理如果一个自治的分数阶系统在平衡点是渐近稳定的,那么平衡点处的雅可比矩阵的所有特征值满足:

式中,eig(MJ) 表示矩阵MJ的所有特征值.由表1可知,对于所有平衡点P–,P0和P+处的特征值,总是存在 |arg[eig(MJ)]|

4.1.3 整数阶系统的动力学行为

为了研究偏置电压Em变化对整数阶忆阻混沌系统的影响,这里选择将参数Em作为变量,取系统初值为 (±0.45 V,0 V,0 V,0 V),当保持系统的其他参数都不变时,绘制的系统分岔图如图7 所示.可以看出系统初值为正,Em=0 时系统处于单周期状态,并随着偏置电压源电压的增大,由倍周期分岔进入混沌态.在初值为负时,系统始终处于周期态,未发生改变.随后图8 和图9 给出了系统由周期态进入混沌态的相图与各平面相图,可以看出与分岔图相吻合.此处所讨论的偏置电压源的变化正是对应于前文的V-I不对称程度概念,都是通过改变偏置电压源的电压,从而研究系统的动力学行为.通过与前文中V-I曲线的不对称程度进行对比分析,发现随着不对称度δ 的下降,初值为正时,系统逐渐由周期态进入混沌态.

（3）完善的工作体系和制度。完善的工作体系和制度，是提高思想政治工作实效性的根本保障和前提，同时也是做好思想政治工作的必要条件，供电企业要紧密结合供电企业的生产经营工作，结合自身实际情况创新开展思想政治工作。要加强对思想政治工作流程的梳理，认真落实意识形态工作责任制，形成闭环管理，加强监督体系建设，并做好思想政治工作机制的分析和研究，在实践过程中总结经验，不断地规范与完善思想政治工作流程，显著提高思想政治工作的实效性。

图7 整数阶系统分岔图,其中红色(+)和绿色(–)分别为系统初值取(±0.45 V,0 V,0 V,0 V)Fig.7.Bifurcation diagram of integer order system,where red (+) and green (–) represent system initial values of(±0.45 V,0 V,0 V,0 V).

图8 不同偏置电压Em 下,整数阶系统由周期到混沌相图,其中红色(+)和绿色(–)分别为系统初值取(±0.45 V,0 V,0 V,0 V)(a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.35 V;(f) 0.6 VFig.8.Phase diagram of integer order systems from period to chaos at different bias voltage Em,where red (+) and green (–)represent initial values of (±0.45 V,0 V,0 V,0 V) for the system: (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.35 V;(f) 0.6 V.

图9 整数阶系统各平面相图 (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3Fig.9.Phase diagrams of various planes in integer order systems: (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3.

4.1.4 分数阶系统的动力学行为

取与整数阶系统相同的初值,直接使用(8)式进行数值仿真,绘制的分数阶系统分岔图如图10所示.随着参数Em的改变,系统由于对称性被破坏,初值为正时系统呈现出周期,随后倍周期分岔进入混沌态,而系统初值为负时,不受偏置电压的影响,并始终呈现出周期态.为进一步验证电压Em的影响,图11 和图12 给出了相对应的系统由周期态步入混沌态的相图与各平面相图.可以看到,系统初值为正,Em=0 V 时系统为单周期态,Em=0.2 V 时为双周期态,Em=0.3 V 时为四周期态,Em=0.32 V 时为八周期态,并随后逐渐进入混沌态.可以看出,虽然对称性的破坏会对初值为正时的系统有影响,但并不会对初值为负时的系统产生影响,验证了上述理论分析的结果.

图10 分数阶系统分岔图,其中红色(+)和绿色(–)分别为系统初值取(±0.45 V,0 V,0 V,0 V)Fig.10.Bifurcation diagram of fractional order system,where red (+) and green (–) represent system initial values of (±0.45 V,0 V,0 V,0 V).

图11 不同偏置电压Em 下,分数阶系统由周期到混沌相图,其中红色(+)和绿色(–)分别为系统初值取(±0.45 V,0 V,0 V,0 V)(a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.4 V;(f) 0.6 VFig.11.Phase diagram of fractional order systems from Period to chaos at different bias voltage Em,where red (+) and green (–)represent initial values of (±0.45 V,0 V,0 V,0 V) for the system: (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.4 V;(f) 0.6 V.

图12 分数阶系统各平面相图 (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3Fig.12.Phase diagrams of fractional order systems in various planes: (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3.

分数阶模型通过分数阶阶次的引入增加了系统的灵活性和自由度.为了讨论阶次对分数阶非齐次忆阻混沌电路性能的影响,取与4.1.3 节中相同的电路参数,当Em=0.4 V,初值为(±0.45 V,0 V,0 V,0 V)时,系统随阶次q1变化的分岔图如图13所示,可知阶次也会对系统产生影响.当初值为正时,系统同样随着阶次的改变,从周期态由倍周期分岔进入混沌态;当初值为负时,系统始终处于周期态,但随着阶次的上升,电压v1缓慢下降.同时,为了探索初值变化时,系统周期与混沌共存的稳态分布,以初值v1(0) 与v3(0) 为变量,系统的吸引盆如图14 所示,其中左边黄色代表周期态,右边蓝色代表混沌态.

图13 系统随阶次变化分岔图 (a) 系统初值为(0.45 V,0 V,0 V,0 V);(b) 系统初值为(–0.45 V,0 V,0 V,0 V)Fig.13.Bifurcation diagram of system with order variation: (a) Initial value of the system is (0.45 V,0 V,0 V,0 V);(b) initial value of the system is (–0.45 V,0 V,0 V,0 V).

图14 含有偏置电压源的分数阶系统吸引盆Fig.14.Fractional order system suction basin with bias voltage source.

4.2 忆阻混沌电路的仿真研究

4.2.1 整数阶忆阻混沌电路

图15 为整数阶忆阻混沌电路实现原理图,电路中的二极管型号选择为1N4148,运算放大器的型号为TL084,系统的参数设置与数值仿真时相同.仿真所得电路由周期态进入混沌态相图与各平面相图如图16 和图17 所示,结果与数值仿真基本一致.

图15 整数阶系统电路仿真原理图Fig.15.Schematic diagram of integer order system circuit simulation.

图16 不同偏置电压Em 下,整数阶系统电路仿真由周期到混沌相图,其中红色(+)和绿色(–)分别为系统初值取(±0.45 V,0 V,0 V,0 V) (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.35 V;(f) 0.6 VFig.16.Circuit simulation of integer order system from period to chaos phase diagram at different bias voltage Em,where red (+)and green (–) represent initial values of (±0.45 V,0 V,0 V,0 V) for the system: (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.35 V;(f) 0.6 V.

图17 整数阶系统电路仿真各平面相图 (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3Fig.17.Fractional order system circuit simulation phase diagrams of each plane: (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3.

4.2.2 分数阶忆阻混沌电路等效实现

实现分数阶非齐次忆阻混沌电路,需要建立分数阶电容的等效电路模型.采用Oustaloup 滤波算法计算分数阶模块的传递函数,然后将传递函数化为零极点的形式,从而等效实现.图18 为分数阶电容的实际等效电路图,通过该模型可以得到分数阶电容等效电路表达式:

图18 分数阶电容等效电路Fig.18.Fractional order capacitor equivalent circuit.

当阶次q1=0.98,q2=0.99,且近似阶数n=5时,近似的线性传递函数为

根据(13)式可以计算出分数阶电容的具体参数值.当分数阶电容与的分数阶阶次分别为q1=0.98,q2=0.99 时,可以得到相应的分数阶电容的等效电路参数值,见表2 和表3.通过对分数阶电容的电路建模(图18)以及对分数阶电容等效电路中电容值和电阻值的求解(表2 和表3),依据图18 中的等效电路模型在PSpice 软件中搭建分数阶电容,其电路原理图见图19.

表2 分数阶电容和 的等效电阻参数Table 2.Equivalent resistance parameters of fractional capacitor and .

表2 分数阶电容和 的等效电阻参数Table 2.Equivalent resistance parameters of fractional capacitor and .

表3 分数阶电容 和 的等效电容参数Table 3.Equivalent capacitance parameters of fractional capacitance and .

图19 分数阶系统电路仿真原理图Fig.19.Schematic diagram of fractional order system circuit simulation.

通过电路仿真,可以得到分数阶非齐次忆阻混沌电路的相图,如图20 和图21 所示.图中显示了分数阶混沌系统从周期态到混沌态的演变,以及混沌态时各平面的相图.通过对比图16(f)与图20(f)相图可以看出,由于受到电容阶次的影响,系统混沌态相图的混沌区域明显减小.从仿真结果发现,分数阶电路仿真的结果与数值仿真的结果基本一致,从而验证了理论分析的正确性.

图20 不同偏置电压Em 下,分数阶系统由周期到混沌电路仿真相图,其中红色(+)和绿色(–)分别为系统初值取(±0.45 V,0 V,0 V,0 V) (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.4 V;(f) 0.6 VFig.20.Simulation phase diagram of fractional order system from period to chaos circuit at different bias voltage Em,where red (+)and green (–) represent initial values of (±0.45 V,0 V,0 V,0 V) for the system: (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.4 V;(f) 0.6 V.

图21 分数阶系统电路仿真各平面相图 (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3Fig.21.Fractional order system circuit simulation phase diagrams of each plane: (a) v1-v2;(b) v1-v3;(c) v1-v4;(d) v2-v3.

5 电路实验

本文选择NI 设备进行混沌系统的硬件实现,其实验原理与实验平台如图22 所示.设备与电脑通过以太网进行通讯,LabVIEW 软件采用的是模块化编程.其中,分数阶实验对分数阶微积分方程进行了近似,实现了分数阶微积分的基本算子,即分数阶积分和导数运算.在NI LabVIEW 软件中搭建好离散混沌系统模型后,进行编译.通过探头将接口连接到示波器上观察系统的相图,得到的整数阶混沌系统,如图23 和图24 所示.分数阶混沌系统相图,如图25 和图26 所示.当Em=0 V 时,整数阶系统与分数阶系统都为单周期共存,并随着Em的增大,正初值时系统逐渐进入混沌,而负初值时系统不受偏置电压Em的影响.实验所得相图与数值仿真,电路仿真相吻合,进一步证明了理论的正确性.

图22 混沌系统实验原理图及实验平台Fig.22.Schematic diagram and experimental platform of integer order system experiment.

图23 不同偏置电压Em 下,整数阶实验由周期进入混沌相图,其中粉色(+)与蓝色(–)分别代表系统初值为(±0.45 V,0 V,0 V,0 V) (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.35 V;(f) 0.6 VFig.23.Integer order experiment from period to chaotic phase diagram at different bias voltage Em,where pink (+) and blue (–)represent system initial values of (±0.45 V,0 V,0 V,0 V),respectively: (a) 0 V;(b) 0.2 V;(c) 0.3 V;(d) 0.32 V;(e) 0.35 V;(f) 0.6 V.

6 结论

忆阻器作为一种重要的非线性元件,因其独特性能具有巨大的应用潜力.由于分数阶微积分对实际电路的描述更加准确,本文提出了一种新型含有偏置电压源的分数阶忆阻器模型,通过对其数学模型的仿真研究,可知分数阶忆阻器的磁滞回线的对称性可以随着偏置电压源Em的值调整.然后结合Jerk 振荡器,构建了一种含有偏置电压源的分数阶非齐次忆阻混沌电路.结合分岔图与相图等手段,分析了Em对系统的影响.结果表明,随着Em的改变,初值为正时,整数阶与分数阶系统都会呈现倍周期分岔进入混沌的动力学行为;但在初值为负时,系统不受偏置电压的影响.随后,建立了分数阶电容等效电路模型,在PSpice 中进行了分数阶非齐次忆阻混沌电路的电路仿真,其结果与数值仿真分析基本一致.最后,在NI 设备上完成了整数阶与分数阶混沌系统的硬件实验.验证了理论分析的正确性,拓展了模拟物理忆阻器不对称磁滞回线的相关理论.