基于支持向量回归的噪声激励下混沌系统的预测

侯文涛,柴鑫杰,赵晓乐

(1.运城学院 数学与信息技术学院,山西 运城 044000;2.北方民族大学 数学与信息科学学院,银川 750021)

混沌系统是指一类非线性动力学系统,表现出一些随机、不可预测的运动行为,其运动过程是高度敏感的,即微小的初始条件差异可能就会导致非常大的行为差异[1]。混沌系统的预测一直是研究者关注的热点问题之一。然而,现实生活中的混沌系统往往还会受到外界噪声的干扰,并且这种干扰是不可避免的[2]。因此在预测混沌系统未来演化的研究中,考虑噪声的影响尤为重要[3,4]。数据科学和大数据背景下, 机器学习技术在各个领域都取得了突出的成果[5-7]。各种具有强大拟合和预测能力的机器学习算法丰富了混沌系统的预测方法[8-13]。支持向量回归(Support Vector Regression, SVR)是一种基于统计学习理论的机器学习算法,它具有强大的泛化能力和较好的预测性能,在非线性系统的预测中具有广泛的应用。因此, 将SVR应用于混沌系统的预测研究,具有很大的潜力和发展前景[14]。基于此,本文旨在基于SVR探讨Gaussian噪声和Lévy噪声激励下混沌系统的预测问题。

1 理论介绍

1.1 支持向量回归

支持向量机[14]的回归算法又称支持向量回归。假设给定一个样本集

Dtrn={(xi,yi)∶i=1,2,…,m},

其中yi∈R,是样本的标签值,那么模型可以表示为

f(x)=wTx+b,

其中w是权重项,b是偏置项。通过计算使f(x)可以和y之间最多可以有的偏差。定义SVR的不敏感损失函数为Lε,表达式为

根据结构风险最小化原则,SVR的结构风险为

(1)

其中C是正则项,即惩罚参数。将(1)式转化为最优问题为

1.2 噪声理论

Gaussian噪声是一种常见的随机信号,其特点是由一组服从正态分布的随机变量构成。正态分布又称Gaussian分布,是一种连续的概率分布,可以用其概率密度函数来描述。因此Gaussian噪声在各个领域中都有着广泛的应用,例如通信、图像处理、声音处理等[3,4]。

许多研究表明,真实的观测数据通常表现为突变或爆发。由Lévy噪声驱动的动力系统可以更准确地对它们进行建模。Lévy噪声表现出大量的微小波动,或有强烈的“跳跃”,有望成为描述非线性系统中固有的随机波动的有力工具。它已经在不同领域被检测到,Lévy噪声扰动的随机模型受到学者们的广泛关注[2]。

1.3 精度计算

本文采用均方误差损失函数(MSE)和相对度量R2评分来评估模型的预测精度和预测性能[3,4]。MSE和R2评分定义为

2 噪声激励下混沌系统预测

2.1 Henon混沌系统

Henon是一种经典的二维动力系统,由法国数学家Michel Hénon在1976年提出[4]。Henon映射的定义为

其中a和b是常数,xn和yn是映射的前一个状态。当a=1.4和b=0.3时,Henon系统表现出混沌行为。

2.2 数据的收集与整理

我们选取Henon映射的控制参数a和b分别为1.4和0.3,初始状态x0和y0分别随机取为0.1和0.1。分量x产生2000点,丢弃初始的10000点,使序列完全进入混沌状态,取之后的10000点构成一维无噪声混沌序列,对Henon系统的混沌状态进行观察。将收集到的10000个数据进行相空间重构,利用自相关法[14]确定延迟阶数为1,Cao的方法[14]确定嵌入维数为3。

为了量化Gaussian噪声和Lévy噪声的影响,我们在无噪声的确定性数据中分别添加了Gaussian扰动和α-稳定Lévy扰动。并且考虑了三种不同的噪声水平,将标准差设置为无噪声数据标准差的0.5%、1%和5%。

将数据划分为训练集和测试集。其中训练集占85%,也即10000点中的前8500点;测试集占15%,也即10000点中的后1500点。

2.3 噪声激励下混沌系统预测

现对0%(无噪声)、0.5%、1%和5%Gaussian噪声激励下的Henon混沌时间序列基于SVR模型进行拟合。SVR网格搜索[15]中,网格搜索取值点如表1所示。

表1 SVR网格搜索超参数取值点

我们一共需要训练3×5×3=45个不同的SVR模型,采用网格搜索的交叉验证方法,从中选取MSE最小的模型超参数作为最优的SVR超参数配置。然后在整个训练集上重新进行一次训练,作为最终的SVR模型。选取时间序列交叉验证的折数为5。以0%(无噪声)数据作为参照,最终选择的模型超参数是:核函数为RBF核,C=100,ε=0.001。将最终选择的模型应用于拟合0.5%、1%和5%Gaussian噪声激励下的Henon混沌时间序列,最终的拟合效果详见图1(a—d)。

a-0%无噪声;b-0.5%Gaussian噪声;c-1%Gaussian噪声;d-5%Gaussian噪声。图1 Gaussian噪声激励下模型拟合预测效果图

同理,将最终选择的模型应用于拟合0.5%、1%和5%Lévy噪声激励下的Henon混沌时间序列。最终的拟合效果详见图2(a—d)。

计算不同水平Gaussian噪声和Lévy噪声下的精度指标MSE和R2,详见表2。由图1(a—d),图2(a—d)和表2可知,随着噪声水平的增加,MSE越来越大,R2越来越小。说明受噪声水平的影响,混沌系统的预测性能越来越差。相比于Gaussian噪声,Lévy噪声对混沌系统预测的影响程度更大。

表2 和随噪声水平的变化表

3. 基于噪声混沌理论的股票价格预测

股票市场是一个充满不确定性的复杂系统,这种不确定性主要是由各种因素的干扰造成,投资者需要通过分析市场趋势来做出决策。在一个较短的时间内股票价格的变化具有很强的规律性,是一种介于随机和确定性之间的混沌现象[16,17]。

虽说股票价格有较强的随机性,但也不是不可预测的。股票市场中最直观的属性便是每日开盘价,而股票每日的开盘价是受前几日的交易情况影响的,并且与最高价、最低价、收盘价和成交量等指标关系紧密。因此选取这四个指标来预测股市短期内的开盘价是有意义的。

3.1 股票价格数据的收集及整理

茅台股票是中国股市中的一只蓝筹股,其价格波动较大。本文借助混沌理论对茅台股票的开盘价进行预测,数据来自于Yahoo Finance网站https://finance.yahoo.com。数据选取的时间段为2010年4月26日到2020年4月24日,共计2426个交易日。

首先验证茅台开盘价数据的混沌性。经计算,x轴的最大李雅普诺夫指数为347.1064,y轴的最大李雅普诺夫指数为192.1266,z轴的最大李雅普诺夫指数为114.1666。三个方向上的李雅普诺夫指数均为正数,说明茅台开盘价数据确实具有混沌特性[18]。进一步,由于五个指标之间的数量级相差十分巨大,所以对原始数据进行归一化处理,使所有数据的取值都集中在0～1之间。最后将归一化后的茅台股票数据分成训练集和测试集,其中训练集包含前85%的数据,测试集包含后15%的数据。

3.2 股票价格数据的降噪

由于股票市场的异常复杂性和非线性,股票数据序列本身是含有大量噪声的,这些噪声肯定会影响预测的准确率和有效性。根据2.3可知噪声会严重影响预测的性能,因此在对股票序列进行预测分析之前,必要对序列进行降噪。

小波变换是一种常用的信号处理技术,可以用来对时间序列数据进行奇异值降噪处理,消除数据中的高频噪声,保留数据中的低频信息[19]。本节使用小波变换对茅台股票价格数据进行降噪处理,降噪结果如图3所示。其中(a)表示降噪前的原始信号,(b)表示经过小波变换降噪后的信号。由图3可知,降噪后的信号比原始信号更加平滑,去除了大部分的噪声信号。

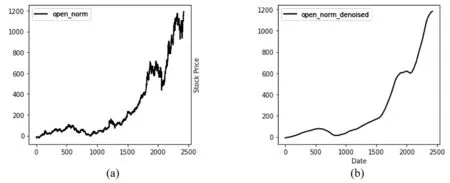
图3 降噪前后股票价格归一化数据比较图,降噪前(a),降噪后(b)

3.3 股票价格的预测

现基于整理好的茅台股票开盘价、最高价、最低价、收盘价和成交量五个指标数据,利用SVR对开盘价进行拟合[20,21]。SVR网格搜索中,网格搜索取值点如表1所示。

最终选择的SVR模型超参数是:核函数为RBF核,C=1000,ε=0.1。SVR在测试集上的均方误差为=7.88389e-07,R2=0.9999890,详见图4(b)。比较未进行降噪的拟合效果图4(a),进一步说明降噪后噪声激励下混沌时间序列的预测精度明显得到改善。

图4 降噪前后股票价格归一化数据预测效果图

4 结论与后续展望

该研究主要探讨了噪声激励下混沌系统的预测问题,并以Henon映射为例,实证分析了Gaussian噪声和Lévy噪声对混沌系统预测性能的影响。研究表明噪声水平越高,混沌系统的预测性能越差。Lévy噪声对混沌系统预测性能的影响远大于Gaussian噪声。接着借助茅台股票价格数据,进一步说明噪声将严重影响混沌系统的预测性能。最后,提出的小波变换降噪法对噪声激励下混沌系统的预测性能有明显改善。

本文基于SVR完成了噪声激励对混沌系统预测性能影响的研究。后续研究工作的重点包括考虑使用神经网络、深度学习等方法提高模型的精度和鲁棒性;考虑从多个方向探索混合噪声及其处理方法,例如基于卷积神经网络,混合神经网络等,提高模型对于噪声的容忍度和预测精度;考虑从多个应用场景出发,探索不同混沌领域中时间序列的应用和预测方法,提高模型的应用价值和实用性。