基于深度学习的电力工程数据异常检测模型设计

王 斌，房向阳，毛 华，孙 岳

（国网天津市电力公司，天津 300010）

电力建设工程对于保障我国经济高速发展具有重要意义。近年来，随着用户用电需求的日益提升，电网公司逐步向高质量能源服务商[1-2]转变。

在推进电力工程的建设过程中，电网公司积累了海量数据，这类数据与电网结构、运行状态等紧密相关[3-5]。然而目前仍未能充分利用此类数据，原因在于：1）虽然数据量较为庞大，但由于整体质量偏低，故无法支撑人工智能算法的训练与构建[6]；2）海量数据之间的内在联系错综复杂，且缺乏高效、精准的智能数据分析方法[7]。

异常数据检测是改善数据质量的关键方法之一，也是深度挖掘数据价值的重要基础。针对此，文中通过深度学习（Deep Learning，DL）算法实现对异常数据的检测，进而有效提升了电力工程数据的质量。

1 改进局部密度因子

在快速密度峰值聚类算法（Clustering by Fast Search and Find of Density Peaks，CFSFDP）中[8-9]，每个数据样本均具有局部密度ρi和距离li两个特征值。其中ρi可表征为：

式中，dij为数据样本xi与xj的距离；de为阈值距离，是算法所设定的参数；φ(·)为函数，其表达式如下：

dij的计算方式为：

由式（1）可知，xi的局部密度物理含义为与xi的距离小于阈值距离de的数据样本个数。li是xi与局部密度大于其自身其他数据点的最小距离，其计算方式如下：

数据样本特征值的大小依赖于距离阈值，通常该值为人工设定，故具有较大的主观性，且较易干扰算法的智能决策过程。

因此，文中在此基础上加以改进。通过计算xi与其他任意一个数据样本间的距离dij，再按照该距离由小到大排序。假设第k个数据样本为Nk(xi)，则数据样本xi的k个近邻数据样本为：

2 基于DAE-GPR的异常数据检测算法

该文基于深度自编码器（Deep Auto Encoder，DAE）与高斯过程回归（Gaussian Process Regression，GPR）理论提出了一种电力工程数据异常检测算法，该算法的结构如图1 所示。其由两部分组成：1）DAE模型，通过具有深层网络结构的编码器-解码器模型实现输入数据的重构；2）GPR 模型，将输入数据的局部密度因子、编码器的输出数据及重构误差等特征作为输入，以完成对异常数据的精准检测。

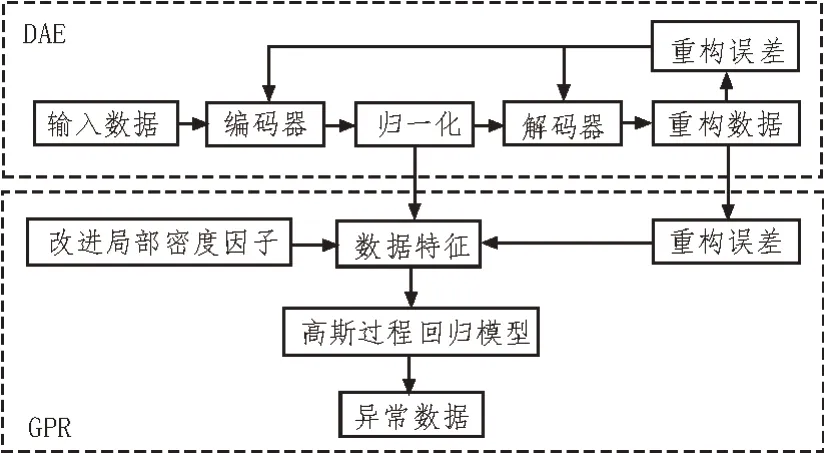
图1 DAE-GPR模型结构

2.1 深度自编码器的结构设计

自编码器是具有对称结构的神经网络模型[10-12]，其核心思想便是在误差尽可能小的情况下对输出层实现输入数据的重构。自编码器的典型结构如图2所示。

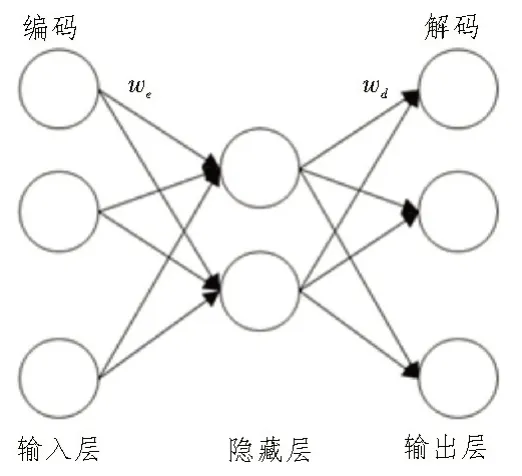
图2 自编码器结构

编码器利用输入数据进行特征提取，且该过程可描述为：

式中，h是编码器输出向量；σe是编码器的激活函数；we和be则分别为编码器的权重矩阵及偏置向量。

而解码器则采用输入数据的特征来实现对其的重构，该过程可描述为：

式中，y为解码器输出向量；σd为解码器的激活函数；wd和bd分别为解码器的权重矩阵和偏置向量。

编码器训练的目标是：令输出与输入间的误差最小化。该训练的损失函数E（W,b）通常为均方误差（MSE）或交叉熵函数（Cross Entropy），二者可定义表征为：

文中提出的深度自编码器结构，如图3 所示。其中编码器包括三个卷积层，且卷积滤波器的大小分别5×5、5×5 和3×3。其通过一个全连接层得到维数为10 的输出，并进行归一化；然后，将归一化后的数据作为解码器的输入。而解码器包括三个反卷积层，卷积滤波器的大小则分别为3×3、5×5 和5×5。

图3 DAE结构

归一化过程可表述为：

式中，xi为编码器的第i个输出；为编码器输出的平均值；zi则是解码器的第i个输入。

2.2 高斯回归

多元高斯分布如下：

式中，x为随机变量；μ为随机变量的均值；C为随机变量之间的协方差矩阵；D为随机变量的维数。

高斯过程回归是使用多元高斯分布模型实现数据回归分析的一种方法[13-14]。通常线性回归采用以下公式来描述输入与输出间的关系：

式中，w为权重变量；b为截距向量。

通常预测值y与实际值f(x) 之间存在一定偏差。因此预测值可描述为：

其中，ε为预测值与实际值之间的偏差，又称之为噪声。

高斯过程回归中，假设噪声ε服从高斯分布：

为了得到回归方程，需求解权重向量w。通常利用似然函数[15-16]进行求解：

由于噪声服从高斯分布，则有：

根据贝叶斯先验概率模型，则有：

因此，权重w的最优解即为式（20）所取得的最大值。由于p(y|x)与w无关，故可转化为：

通过分析可知，式（20）的值服从多元高斯分布：

则能够得到权重的最优值为：

2.3 算法性能评估

对电力工程数据的异常检测结果存在表1 所示的几种情况。

表1 检测结果

召回率pRecall和假正率pFPR计算方式如下：

若pRecall越接近1 且pFPR越接近0，即表明检测算法的性能越优。但当不同算法中这两个指标相近时，则无法进行简单判断。此时通常采用ROC 曲线方法加以判定，其以pFPR为横坐标、pRecall为纵坐标。在ROC 曲线下，面积AUC 是归一化数值，可作为衡量算法性能的指标，且AUC 的值越大表明算法的性能越优。

3 算例分析

为验证所提DAE-GPR 算法的准确性，采用了某省电网公司近五年来的2 568 条电力工程数据作为测试数据集，并进行了仿真。

3.1 算法性能分析

将所提算法与DAE、自编码器（Auto Encoder，AE）算法进行比较，三种算法的迭代收敛过程如图4所示。从图中可看出，三种算法在15～20 次时的迭代接近收敛，且收敛速度差异较小。但所提算法在最终收敛时的AUC 值为0.892，而DAE 和AE 算法分别为0.873 和0.860。由此表明，该文算法的异常数据检测性能更优。

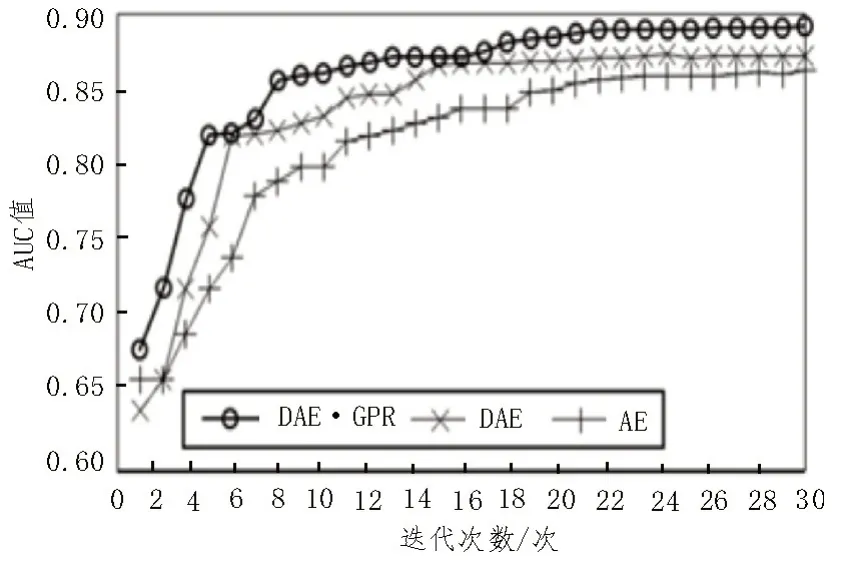
图4 算法迭代收敛过程

对比分析测试数据集异常率在10%、20%、30%、40%和50%情况下，三种不同算法的AUC 值。具体结果，如图5 所示。可以看到，当数据异常率从10%上升到50%时，DAE-GPR 算法AUC 值仅降低了0.092，而DAE 和AE 算法的AUC 值则分 别下降 了0.192 和0.262。由此说明该文算法受数据异常率的影响较小，算法稳定性较强。

图5 数据异常率对检测结果的影响

3.2 应用效果分析

进一步将所提算法应用于某电网公司2022 年以来的209 条电力工程数据中。数据异常检测结果，如图6 所示。由图可知，工程量与费用数据的异常占比均在40%以上，且二者之和超过了90%，而技术条件数据的异常占比则小于10%。因此在电力工程数据的管理过程中，可通过加强对工程量与费用类型数据的校核管控，从而提升电力工程数据的质量。

图6 数据异常检测结果

4 结束语

文中开展了深度学习算法在电力工程数据异常检测中的应用研究，并提出了DAE-GPR 算法，以实现对异常数据的精准检测。通过仿真算例表明，所提算法的AUC 指标优于DAE 及AE 算法，且具有更高的异常数据检测性能。同时，其受数据异常率的影响也较小，稳定性良好。实际应用结果表明，电力工程数据中工程量与费用类型的数据异常占比超过了90%，因而需要加强对这两类数据的管控。但该文算法无法实现对异常数据的修正，这将在后续工作中开展。