下推式磁悬浮自适应模糊PD 控制方法

林厚健，蔡子颖，邓定南，王小增，黄杰贤

（嘉应学院物理与电子工程学院，广东梅州 514015）

磁悬浮系统具有无接触、无摩擦以及近乎无阻力的性能特点被大众所追求，通常应用于磁悬浮轴承[1]、列车和摆件等，控制方法也多种多样[2]。但磁悬浮系统具有非线性、不稳定、抗干扰差等特点，若采用依赖数学模型的控制方法[3]，将使得系统的控制变得复杂，对MCU 的算力要求更高，而模糊PID 虽然适应能力强，但稳态控制效果通常不如模型预测和神经网络等控制算法，且以上算法实现起来相对复杂。基于以上分析，文中设计了一种采用模糊PD 控制与自适应算法相结合的改进下推式磁悬浮系统，相比常规PD 控制算法的磁悬浮控制系统，适应范围更大，鲁棒性更强，功耗更低。

1 磁悬浮系统分析与搭建

钕铁硼浮子在斥力和吸力的共同作用下，竖直方向上的浮子达到受力平衡而悬浮。

又由恩绍定理[4]知，磁悬浮系统水平方向上若没有对浮子的控制作用，浮子是难以稳定悬浮的。为提供磁悬浮系统水平方向上的控制力，实验模型中，在铁氧体环内对称放置四个磁力线圈，水平方向控制力随线圈电流变化而变化。在铁氧体环内中心位置放置三个相互垂直的线性霍尔元件HX6639，用于检测该点的三轴磁场信息，通过STM32F401 主控芯片读取并转换得到浮子的位置信息，并进行控制算法的运算，通过驱动器控制磁力线圈输出力的大小，实现对浮子的稳定悬浮控制。

2 模糊PD自适应控制器的设计

2.1 PD控制器

传统PID 控制器中，控制量输出U(t)与控制误差err(t)关系如式（1）所示：

根据磁悬浮系统的特点，除了控制浮子的位置之外，还要抑制浮子震荡速度，因此引入微分环节，人为放置浮子时的起始控制位置和动作完成时间是不确定的，若加入积分环节，会因为放置浮子的动作容易引起积分饱和，使得浮子在稳态时出现明显振荡，所以去除积分控制，采用PD 控制。PD 控制算法的离散化公式如式（2）所示：

其中，err(k)为k时刻的偏差，Kp和Kd分别是比例和微分参数。

2.2 模糊PD控制器

传统PD 控制的磁悬浮系统效果不尽如人意，基于以上PD 控制算法，应用模糊控制理论，实现PD 参数的在线自整定，以提高系统的鲁棒性和适应性。图1 所示为模糊PID 控制结构图。

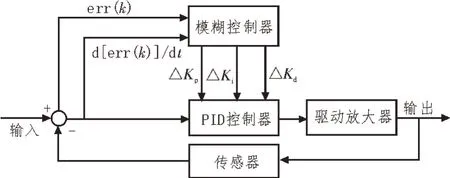
图1 模糊PID控制结构图

模糊控制器主要由模糊化、模糊推理和解模糊三个环节组成[5-10]。首先对输入值模糊化，以误差err(k)和误差变化率Δerr(k)作为输入，确定输入量的基本论域，再通过实测对PD 参数的基本论域进行确定。

选定负大[NB]、负中[NM]、负小[NS]、零[ZO]、正小[PS]、正中[PM]、正大[PB]七个语言变量表达err(k)和Δerr(k)的模糊子集，选择合适的常数集{-300，-200，-100，0，100，200，300} 作为模糊子集，通过测试，得出表1 所示系统模糊参数,其中量化因子为基本论域和模糊论域之比。

表1 系统模糊参数

接着求解输入数据的隶属度，这里选用三角隶属度函数，通过隶属度函数，计算当前偏差数据对应的隶属区间和隶属度，完成对偏差数据的模糊化，然后进行模糊推理，得出清晰化的数值增量。根据PID参数的工程整定法，可制定PD 参数的模糊规则表。结合模糊规则表，通过重心法[11]进行解模糊，如式（3）所示：

其中，M为隶属度，F为模糊量化值，Vo为模糊输出增量，由式（3）可得PID 参数的增量值ΔKp、ΔKd，即系统PD 参数表达式如式（4）所示：

式中，Kp0和Kd0为使用模糊参数整定前的初始值。

2.3 自适应模糊PD算法

为了尽可能消除稳态误差，同时最大程度降低系统的稳态输出功率，该系统引入自适应控制算法。自适应控制算法包括自学习的控制算法[12-13]、基于backstepping 方法设计的自适应算法[14]、滑模自适应算法[15-16]、反馈线性化与在线参数辨识相结合的非线性自适应控制方法[17]和采用Lyapunov 综合设计方法的模糊自适应算法[18]等。以上自适应控制算法虽然能降低甚至消除系统稳态误差，但实施难度相对较大，而且都是基于恒定设定值而设计的算法。

通过式（5）对偏差进行分析：

式中，set_goal(k)为k时刻的设定值，detection(k)为k时刻的检测值。err(k)的大小取决于设定值与检测值的差，检测值是由控制情况所决定的，而设定值是控制开始前设定且认为是浮子最佳悬浮位置的固定参数，对浮子的控制开始后，该固定参数往往已不再是浮子的最佳悬浮位置，故令系统实时调整设定值并使浮子自动寻找合适的悬浮位置实现稳定悬浮。

动态调整设定值之前，需先使系统进入稳定悬浮状态，而Δerr(k)趋近零是稳态的特点，假定误差变化率|Δerr(k)|＜a，其中a＞0，认为系统进入稳态。认定系统进入稳态后，假定稳态误差控制目标为|err(k)|＜b，其中b＞0，当|err(k)|＞b时，设定值就对err(k)进行积分累加，向|err(k)|增大的方向调整，进而使|err(k)|更大，迫使系统自动调整浮子位置。随着系统的调整，浮子的稳态误差逐渐减小，处于动态调整的设定值也会逐渐稳定，直到满足|err(k)|＜b，式（6）为设定值调整的理论依据：

其中，c为设定值积分系数。引入以上算法进行改进后，实现了设定值自动调整的自适应控制，稳态误差几乎为0。

实验中发现，对受控力较小的浮子进行控制时，系统容易因输出磁力不够而失控。针对这一问题，利用检测z轴磁场的霍尔元件来判断浮子的受控力大小，对PD 参数再加入一个随受控力变化的控制增量，如式（7）所示：

其中，VMAX为z轴检测量程的最大值，z_detection(k)为k时刻检测值，α和β为增量比例系数，均大于0。

自适应模糊PD 算法控制结构图如图2 所示，在传统PD 控制的基础上，引入了增加设定值积分功能的自适应模糊控制器和基于z轴磁场检测的比例控制器对PD 参数进行自动调整，进而提高控制系统的鲁棒性和适应性。

图2 自适应模糊PD算法控制结构图

3 实验数据处理与分析

实验电路采用自主设计的基于STM32F401CCU6为主控芯片的磁悬浮硬件系统，控制代码在Keil 软件开发环境下通过C 语言编写完成，浮子位置跟踪波形通过蓝牙模块传输数据到手机蓝牙串口调试器APP 进行显示。

3.1 浮子的位置跟踪误差测试

实验确定的钕铁硼浮子直径、厚度、质量分别为3 cm、2 cm、96 g。依次用传统PD 控制、模糊PD 控制、自适应模糊PD 控制算法进行悬浮控制实验。确保三种控制算法初始PD 参数相同，钕铁硼浮子在传统PD控制、模糊PD 控制、自适应模糊PD 控制算法下的位置跟踪波形如图3-5 所示。由位置跟踪波形图可知，采用自适应模糊PD 控制使得浮子竖直方向（对应y轴）、水平方向（对应x轴）的位置跟踪误差均趋于0。

图3 传统PD控制下位置跟踪波形

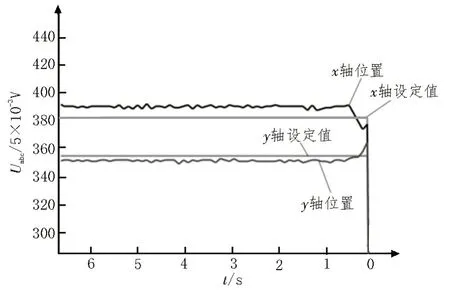
图4 模糊PD控制下位置跟踪波形

图5 自适应模糊PD控制下位置跟踪波形

3.2 系统功耗测试

保持初始PD 参数一致，分别用传统PD 控制、模糊PD 控制和自适应模糊PD 控制对浮子进行悬浮测试直至稳态，通过功率表测量得到磁悬浮系统的稳态输出电流和功率如表2 所示。

表2 系统稳态输出电流和功率

表2 数据表明，自适应模糊PD 控制的稳态输出电流远低于其他两种算法，系统功耗为0.534 W，功耗降低至传统PD 控制的9.5%。

3.3 系统体位适应性测试

为了测试三种控制算法对浮子的体位适应性控制效果，在保证初始PD 参数和位置参数一致的前提下，分别用三种控制算法进行控制直至稳定悬浮后，固定装置的一侧，将另一侧缓慢抬起使装置与水平面夹角增大，直至浮子无法悬浮，并记录稳定悬浮的最大倾斜角和系统输出功率。测试结果为：传统PD控制、模糊PD 控制和自适应模糊PD 控制下的最大倾斜角分别为10°、15°、90°，对应输出功率分别为14.06 W、13.02 W、0.595 W。实验结果表明，在自适应模糊PD 算法控制下，装置倾斜角能够达到90°，系统功耗由14 W 降低至0.6 W 左右，性能明显优于前两种控制算法。

4 结论

针对常见下推式磁悬浮系统存在的稳态误差大、系统功耗高、体位适应性差的问题，提出了一种自适应模糊PD 控制算法，在传统PD 控制的基础上加入模糊控制，降低了浮子位置稳态误差。引入具有设定值积分功能的模糊控制器和基于z轴磁场检测的比例运算器实现自适应模糊PD 控制，使系统具有设定值自调整功能。实验结果表明，相较于传统PD 控制和模糊PD 控制，基于自适应模糊PD 控制算法的磁悬浮系统输出功率显著下降，同时装置悬浮倾斜角从10°达到90°几近垂直状态，磁悬浮控制系统的稳态误差、系统功耗、体位自适应能力三方面的性能均得到大幅提升。