基于层次聚类的终端波形相似度评价方法

施昕昕，张旭辉

（南京工程学院，江苏南京 211167）

配电终端是整个配电网系统的关键健康感知单元，覆盖率也随着配网工程的开展而日益提高，为保障设备的操作安全性，并达到对配电终端的精益化运维目标，故对其健康状况评价进行研究[1]。配电终端具有数据采集及传输的功能，同时能够实现对配电网故障的检测和自动监控，其自身的运行可靠性与稳健性对于配电网系统的稳定运行起到重要的作用[2]。其采样波形可反映实际录波过程中测试系统存在的问题，包括信号的噪声干扰、抖动、增益，以及采样率带来的波形不准确问题。

目前，有许多方法可对配电终端的健康进行评价，文献[3]中通过高精确性的隶属函数判断对配电终端的健康指标隶属程度，但并未考虑复杂系统的随机性。文献[4]针对配电自动化二次设备健康因素评估问题，选取了影响配电二次设备的运行状况、环境状况和巡检状况作为评估对象，但不能反映终端的实时健康状态。文献[5]采用了集成客观事物随机性和模糊度信息的云模式求解指标隶属度，但由于评价指标中所包含的系统自身在工作环境要素中的有关硬件状态，以及工作环境因素的信息一般在配电智能化系统中并未收集，所以这种评价模型在实际运用中无法达到理想的目标。

为此，首先根据业界专家建议、有关文献和研究，对终端所录波形与功率源标准波形特征进行分析。将录波器所录功率源的波形作为源波形，将终端所录波形作为测试波形，采用DTW 距离算法，计算两波形的距离，将输出结果作为对电源波形与试验波形之间相似程度的判断结果值，并采用层次聚类算法将配电终端的健康状况区分为异常、注意和正常三种，分别对应波形相似度中的相似、疑似相似以及不相似；对于多种影响因素，通过层次分析法构造判断矩阵，定义指标权重，将指标权重与聚类结果相结合得到终端波形相似度评价方法。

1 理论依据

1.1 DTW计算距离

DTW 作为一种非线性动态规划算法，通过时间序列数值上的相似性对时间轴进行规整[6-7]。两个波形序列X和Y，长度依次是|X|和|Y|，对其进行相似度比较。令一条曲线W=w1,w2,…,wk为规整路径，规整路径的长度大于两序列的长度且小于两序列长度之和[8-9]。W从w1=(1，1)起始，一直延伸至wk=(|X|,|Y|)，以此来保证W中可以包含X和Y中的所有位置。另外，W中w(i,j)的i和j值应该是单调递增的，以确保其曲线不交叉，即点w(i,j)和点wk(i′,j′)需要满足以下关系：

规整代价最小的路径为：

最后，要获得的规整路线必须是相对距离最短的一条规整路线，如下：

路径从左下角出发，采用步进模式一直匹配至右上角，即求解扭曲曲线[10]，扭曲曲线需要保证匹配路径过程中经过的元素值总和最小。DTW 距离计算过程中，波形通过对单位点进行复制，达到局部范围内的缩放调整，在此基础上可以很好地进行对齐匹配[11-13]。

规划路径满足以下的约束:路径从上一个方格(i-1,j-1)或者(i-1,j)或者(i,j-1)中到下一个方格(i,j)，如果是从(i-1,j)或者(i,j-1)规划，其距离为d(i,j)，而如果是从(i-1,j-1)规划，其距离为2d(i,j)，两个波形序列之间的距离计算如式（4）所示：

式中，g(i,j)表示两个波形序列之间的距离不断叠加以得到最小值dist(X,Y)。

采集大量数据样本后，将距离归一化后得到dist′(X,Y)，再把相似距离通过式（5）转化为相似度：

1.2 改进的层次聚类法

1.2.1 层次聚类

对上述波形经比对后计算得出的最小间距进行归一化处理，将其作为对数据的层次聚类计算，即输入n个样本数据，经层次聚类输出m个合集分类[14]。

步骤包括：

1）计算n个样本两两之间的距离；

2）构造m个类，每个类只包含一个样本；

3）合并类间距离最小的两个类，并将最短距离作为类间距离，构建一个新类；

4）计算新类与当前各类的距离。若类的个数为1，终止计算，否则回到步骤3）。

层次聚类流程图如图1 所示。

图1 层次聚类流程图

经过层次聚类算法可以有效将距离分成三类，得到最小距离的聚类中心点ctr1和ctr2，将其中心点的值作为标准距离值，通过式（6）和式（7）转化为相似度：

当相似度处于ω1与ω2之间时，波形被判断为疑似相似；当相似度处于ω2与1 之间时，波形被判断为相似；当相似度处于0 与ω1之间时，波形被判断为不相似。实际应用中，计算录波仪和二次终端采集波形的相似度，并与海量数据处理后的聚类结果进行对比，判断相似度区间，得到两波形的相似情况，完成终端录波功能状态的评估。

1.2.2 算法改进

比较离差平方和判断两类距离，因为若两类被归为同一种，而它们的距离本身又并非同一种，其离差平方和会差别很大。离差平方和[14]:对一类中每个元素与该类其他元素之间的平均距离值，进行平方并求和，设x为一种随机变量，η=x-Ex，则Ex为η与x相互之间的平均离差，得出x与其数学期望Ex相互之间的偏差范围为SS=∑(xi-)2，其中SS 为离差平方和，xi为第i个点所在的位置，为已完成聚类的某一类的平均距离。

1.3 层次分析法

1.3.1 评价指标的建立

配电终端波形相似程度评估指标设置是否合理，对判断的正确性产生很大影响，所以在判断配电终端波形状态上，必须要形成一套科学合理且完备的指标体系。检索大量资料及听取电力行业众多专家学者建议，形成了终端波形相似性评估指标，涵盖了信号的平面分量和垂直分量等，如图2 所示。

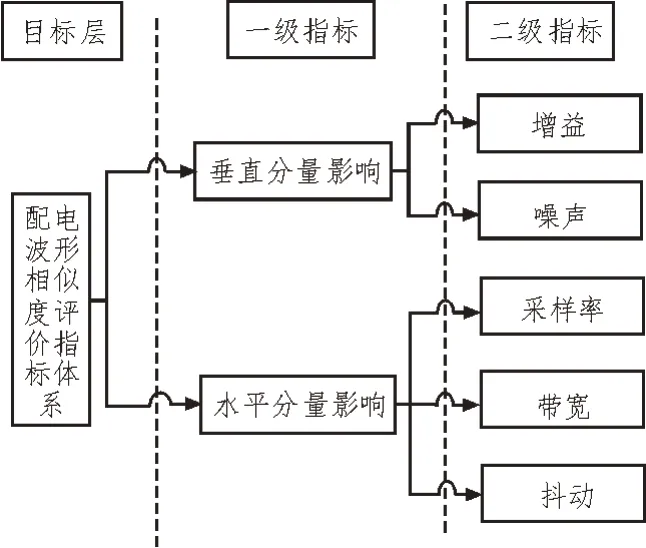
图2 配电终端波形相似度评价指标体系

1.3.2 指标权重的构建

为上述体系构建指标权重，主要包含以下步骤：

1）构建影响波形准确的因素，分为两层因素指标；其中第一层为垂直量和水平量；垂直量二级指标分成噪声和增益，水平量二级指标分成抖动、带宽和采样率。

2）建立判断矩阵，对五种因素两两之间的重要性进行比较，再根据指数取值范围确定，即将A 与B两种指标进行比较，按照表1 的指标取值范围定义A与B 相比的重要程度，作为判断矩阵的元素值。

表1 指标取值范围

根据层次结构建立判断矩阵[15-16]，将同一层次的元素两两比较，假设某层包含n个元素，由X1，X2,…,Xn所构成的n阶判别矩阵为Q=(qij)n×n，当中qij代表元素Xi与Xj对于上面某一元素的重要程度，判别矩阵Q=(qij)n×n即为一正互反矩阵[17]。

3）求取判断矩阵的最大特征值，并对其归一化处理后进行排序。

4）一致性检验。若正互反矩阵Q=(qij)n×n满足qij·qjk=qik(i,j,k=1,2,…,n)，则Q是完全一致阵。最大非零特征值λmax的一致性指标（Consistenxy Index，CI）求取方法为：

CI 越趋近0，说明一致性越好。若CI＜0.1，则说明判断矩阵具有一致性；若CI≥0.1，则重新构造判断矩阵，随机指标（Random Index，RI）值如表2 所示。

表2 平均随机一致性指标

一致性比率求取方法为：

第k-1 层m个元素的权重为：

则k层的n个元素第j个元素权重为：

则k层元素合成权重为：

第k层的一致性检验指标计算方法如下：

5）将1）、3）中五种二级指标填充进判别矩阵，用几何平均法求权值，先将矩阵A的同一行元素相乘构建一组新的列矢量，接着再将新的行向量的所有分量开n次方，最后再对各列矢量加以归一化得出权重向量。

1.4 实验步骤

综上，提出一种配电终端设备波形比对评价方法，算法流程如下：

1）利用DTW 算法计算不同状态下源信号波形与受干扰终端波形的动态时间规整距离，形成大量样本数据。

2）将计算得到的样本进行层次聚类，将距离分成三类，对应不同的终端波形状态。

3）通过层次分析法计算各影响因素的权重指标。

4）将同一指标下步骤2）计算得到的距离与步骤3）得到的权重相乘并累加，最终得到一个相似度范围，该范围适用于普遍情况下的相似度评估范围。

测试主站对功率源波形和一二次融合设备的待测二次终端采集到的波形相似度进行比对计算，对待测二次终端进行健康评估。终端设备波形对比评价方法流程如图3 所示。

图3 终端设备波形比对评价方法流程

2 实验验证

2.1 实验平台

图4 为一二次深度融合成套设备自动检测装置的现场应用情况。该系统可具有终端检测、变压器检测和主次完整检测功能。通过一二次信号切换装置的配合，系统可以一次完成所有测试项目，有效提高检测效率。

图4 一二次深度融合成套设备自动检测装置的现场应用

以搭建的一二次深度融合设备检测平台为研究对象，其终端录波系统如图5 所示。

图5 终端录波系统

PC 机通过协议下发波形给电子式信号源，电子式信号源输出波形至终端，PC 机通过104 协议读取波形数据，采样速率设置为200 kS/s。PC 机设置录波仪触发方式后，录波仪自动采集电子式信号源输出的波形。PC 机读取录波仪的波形数据和104 协议读取的波形数据后生成波形的时间序列，将功率源波形与终端采样波形进行波形对比，得到两波形的相似度。采集大量不同健康状态下的终端数据后，对样本数据进行聚类分析，得出相似度衡量的标准，将相似度分为相似、疑似相似及不相似，对应终端的三种健康状态程度，并构建样本数据库。判断终端健康状态时，对采集的波形进行相似度分析后对比样本数据库，判断终端的实时健康状态，PC 机算法在Matlab 2020a 上实现。

2.2 DTW计算

选取前5 后9 一共14 个周期作为采样周期，将不同情况的源信号波形与终端采样波形的波形时间序列作为输入，使用DTW 算法对两组波形时间序列进行最小距离计算，图6 为源信号波形与噪声干扰下终端采样波形波形序列的点位匹配情况，图7 为两组波形的路径规划图。

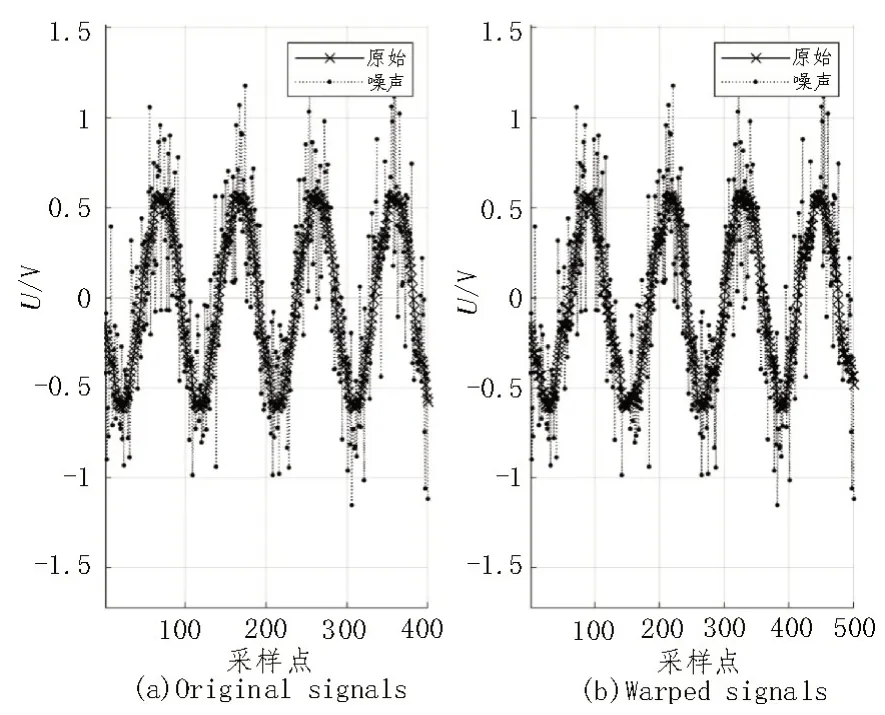
图6 DTW下波形点位匹配图

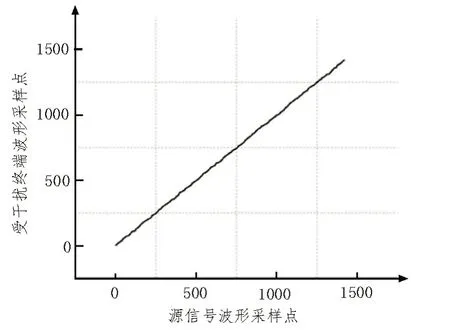
图7 动态路径规划图

2.3 层次聚类

使用层次聚类算法对DTW 算法计算得到的波形距离进行聚类分析，图8 为层次聚类算法下不同类别数的轮廓值，图9 为基于离差平方法和的层次聚类算法下不同类别数的轮廓值，分析得出在分为3 类时，基于离差平方法和的层次聚类算法轮廓值负值更少，优化效果明显。

图8 层次聚类算法轮廓值

图9 优化后的层次聚类算法轮廓值

图10 为基于离差平方和的层次聚类算法对噪声干扰情况下的终端波形与源信号波形之间DTW距离的聚类结果，首先对距离进行数据归一化，将其输入层次聚类算法，分成3 类，找到聚类的中心点，通过式（6）和式（7）转换为相似度。图11 所示为聚类过程中的树状图，体现了聚类算法下类间合并的过程，在适当位置截取，选择聚类的类别数量。

图10 基于离差平方和算法的层次聚类结果

图11 基于离差平方和算法的层次聚类树状图

在噪声干扰、信号抖动、幅值增益、带宽以及采样率对波形影响的情况下，分别计算源信号波与终端采样波形的距离，基于离差平方和算法的层次聚类对这些情况下的距离分别进行聚类，得到聚类中心，并通过式（6）和式（7）转换成相似度，计算结果如表3 所示。

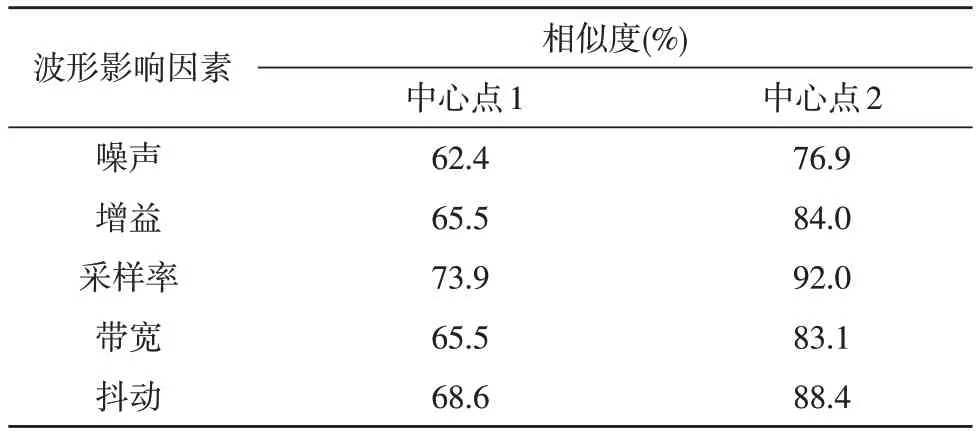
表3 基于离差平方和算法的层次聚类波形相似度

2.4 层次分析结果

根据该文建立的评价指标体系，构建判断矩阵，权重求解。最终获得各个指标的权重如表4 所示。

表4 层次分析算法下的各指标权重

将2.3 中的聚类结果与权重指标相结合，得到适用于全局的终端波形相似度评估指标结果，将表3中的中心点相似度与表4 中各个情况的权重相乘，得到适用于终端采样波形信号全局对比的相似度指标，分别为67.85%和84.81%。实际应用中，计算源信号波形与终端采集波形的相似度，当波形相似度处于67.85%和84.81%之间时，波形被判断为疑似相似；当相似度大于84.81%时，波形被判断为相似；当相似度小于67.85%时，波形被判断为不相似，以此完成对终端健康状态的评估。

3 结论

该文提出了层次聚类与层次分析相结合的配电终端波形相似度评价方法，将DTW 计算得到的波形距离作为样本输入层次聚类算法进行聚类，并采用了层次分析法给予各信号不稳定情况的指标权重，提高了结果判断的科学性。通过算例仿真，采用所提的层次聚类与层次分析相结合的方法对波形相似度进行分析，提出了适用于终端采样波形信号全局对比的相似度评估方法，验证了该方法可以为配电终端的健康状态评估提供数据支撑。