结合遗传算法的水库汛限水位动态控制模型研究

赵鲁斌,宋晓丹

(山东水利职业学院,山东 日照 276800)

0 引 言

为了适应社会的发展,对汛限水位进行优化研究十分必要。汛期是我国大部分地区的主要降水时间,由于汛期降水量较大,若不及时调整限制水库的汛期水位,则水库水位会快速提升,可能导致漫坝甚至垮坝等情况发生[1]。因此,在汛期对水位进行调整,可以起到防洪的效果。同时,我国发电形式主要还是以火力发电为主,但在“环保节能”及“碳中和”的背景下,水电的发展已经成为重点关注对象。水库汛限水位的调整,对提高水库发电效益有明显作用,但防洪效益与发电效益之间存在一定矛盾。因此,实现水库汛限水位的动态调整,即可同时实现防洪效益与发电效益[2]。

1 基于遗传算法的水库汛限水位动态控制模型构建

1.1 遗传算法的优化

遗传算法是一种在工程领域较为常用的优化算法。该算法将原始数据作为初代种群,模仿自然法则中的基因遗传,实现个体的优化[3-5],并经过多次遗传筛选,最终得到种群最优个体,即问题最佳解。遗传算法具体流程见图1。

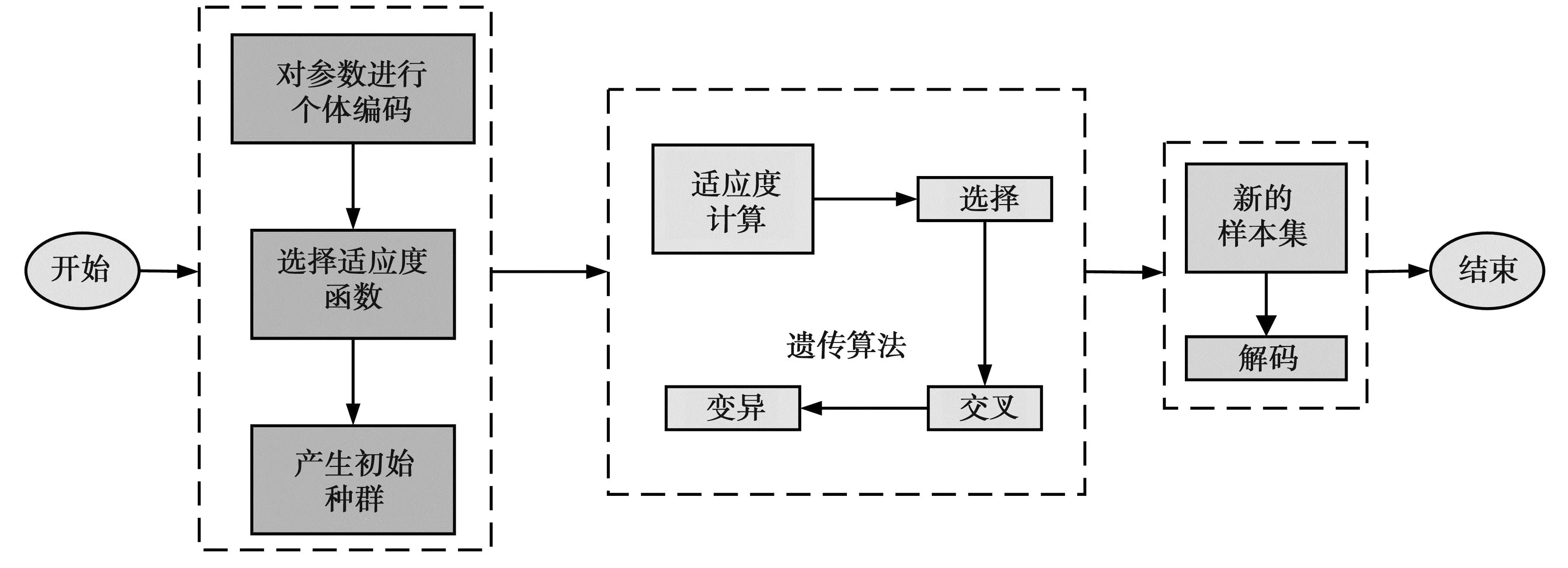
图1 遗传算法具体流程图

图1中,遗传算法通过对实际问题进行分析,并将问题进行编码,确定遗传算法中的适应度评价函数;然后通过遗传操作,形成适应度较高的种群;重复上述步骤,直至算法收敛或达到最大迭代次数。其中,遗传操作包含种群选择、交叉操作以及变异操作。但标准遗传算法的收敛速度只能满足求解简单问题,当面临复杂问题时,该算法则存在易陷入局部最佳解、搜索效率较低等问题。因此,研究对标准遗传算法进行改进。

应用遗传算法首先要解决的问题是编码操作。编码方式的好坏可决定遗传算法的运行效率。二进制编码、实数编码、浮点编码、格雷码编都是遗传算法常见的编码方式,针对水库水位调整问题,研究采用具有高效率、简单且应用广泛等特点的实数编码。

遗传算法第二步是确定适应度函数,该函数是遗传算法中判断个体进化优劣的重要指标。因此,适应度函数的质量对进化方向以及算法运行效率都具有重要作用。针对水库水位调整问题,选择线性变换适应度函数,该函数表达式如下:

f′=αf+β

(1)

式中:f为初始适应度;α、β均为变换系数;f′为经线性变换的适应度。

函数的变换系数选择,需满足两点要求:①变换前后所有个体适应度的平均值应满足相等;②变换后个体最大适应度值与初始种群的平均适应度值呈一定比例关系。因此,变换系数的计算方式如下:

(2)

式中:C为常数,取值范围[1,2];fmax为最大适应度值;favg为平均适应度值。

线性变换适应度函数避免了算法早熟、后期效率低下的问题[6-7]。适应度函数确定之后是遗传操作,遗传操作包括选择、交叉与变异。选择操作是在样本属性中选择可解决问题的属性,将选择的属性进行重新组合,得到新的样本,样本的质量决定了算法的输出结果,样本的选择方法常用比例选择[8]。交叉操作是将相配对的染色体通过一定手段将部分基因进行交换,以此获得新的个体[9]。变异操作是将染色体中的某些基因进行替换,以此形成新的个体[10]。研究在交叉与变异操作进行优化,选择自适应的交叉变异概率,计算公式如下:

(3)

式中:pc为自适应交叉概率;pm为自适应变异概率;pc1、pc2为交叉概率的上下限值;pm1、pm2为变异概率的上下限值。

改进后的自适应交叉变异率,能使适应度较高的个体交叉率与变异率不再接近于0,而是将其概率变化至pc2与pm2,保证种群进化的活力,以此避免算法陷入局部最优解的情况。

1.2 水库水位动态调整中的遗传算法应用

根据遗传算法基本运行方式,现将遗传算法应用水库水位的动态调整中。不同的水库均有一个汛限水位值,对水库水位调整就是对汛限水位进行优化。研究采用实数编码,将汛限水位的原始值作为编码值,并对编码进行解码,计算后水库库容不小于给定的值。假设存在3个水库,对汛期的水库库容进行分配,则实数编码后的形式见图2。

图2 水库汛期库容的实数编码

解码是对图2中的9项参数进行运算。根据查询水位-库容关系曲线,得到汛期期间各水库的库容值。给定的水库库容最小值需满足式(4)要求:

(4)

式中:V1为上旬的库容值;V2为中旬的库容值;V3为下旬的库容值。

若枯荣最小值不满足式(4)要求,则舍去当前水位值,并重新生成水位值。对库容分配进行优化的主要目的是为得到一组汛期水位值,该水位值可在式(4)的约束条件中,使目标函数的值最大。因此,在经过实数编码后,以这些汛限水位值代替原始时段的汛限水位值,然后对水库进行调度计算,最后得到相应的目标函数值,并将该值作为适应度函数值。在汛期水位调整中,研究采用单点交叉的交叉操作,交叉操作形式见图3。

图3 单点交叉过程示例图

图3中,在染色体上随机选取一个交叉点,将染色体分成前后两部分,在交叉点前部分或者交叉点后部分进行基因交换,产生新的子代个体,这一过程为交叉操作。需要注意的是,交叉操作之后可能会出现适应度值小于原有适应度值的个体,即水库库容的值小于给定库容值,此时则需对交叉操作进行调整。假设经交叉后的染色体,在汛期上旬的库容值小于给定库容阈值,则需要对总库容进行增大,其汛限水位需下降。调整步骤如下:第一步,利用水位库容关系,计算该染色体上汛期上旬水库汛限水位所对应的库容值,并将各库容值进行总和,得到总库容值,再计算各水库的库容比;第二步,计算库容阈值与当前计算库容的差值,并将该差值按照第一步所得的库容比,分配至各水库库容中;第三步,判断增加的库容是否超过该水库库容的上限值,若已经超过,则该水库库容值直接取库容上限值,多余部分按照比例分配至其他库容;第四步,利用水位库容关系,反向对汛限水位值进行求解,以得到的汛限水位代替交叉后的汛限水位值。

交叉操作与调整措施结束后,进行变异操作。变异操作是将某个汛限水位值进行替换,替换值为水位可行域范围内的随机值。变异操作与交叉操作类似,变异之后同样会出现不满足库容约束条件的情况,变异操作的调整方式只需重新随机选取水位值即可,直至满足约束条件。

2 基于遗传算法的水库汛限水位动态控制的实际应用效果分析

2.1 水库汛限水位优化

研究将提出水位控制方法在山东峡山水库进行应用分析。峡山水库控制流域面积4 210km2,总库容14.05×108m3。根据计算方式,将水库入库流量作为输入数据进行计算,并确定改进后遗传算法的基本参数。改进后,遗传算法的最大迭代次数为200;初始种群大小为50;算法的选择概率值为0.7;算法交叉概率值0.5;变异概率值0.03。根据水库对应规则,计算不同级别洪水条件的调度结果。水库对应的调度规则见图4。

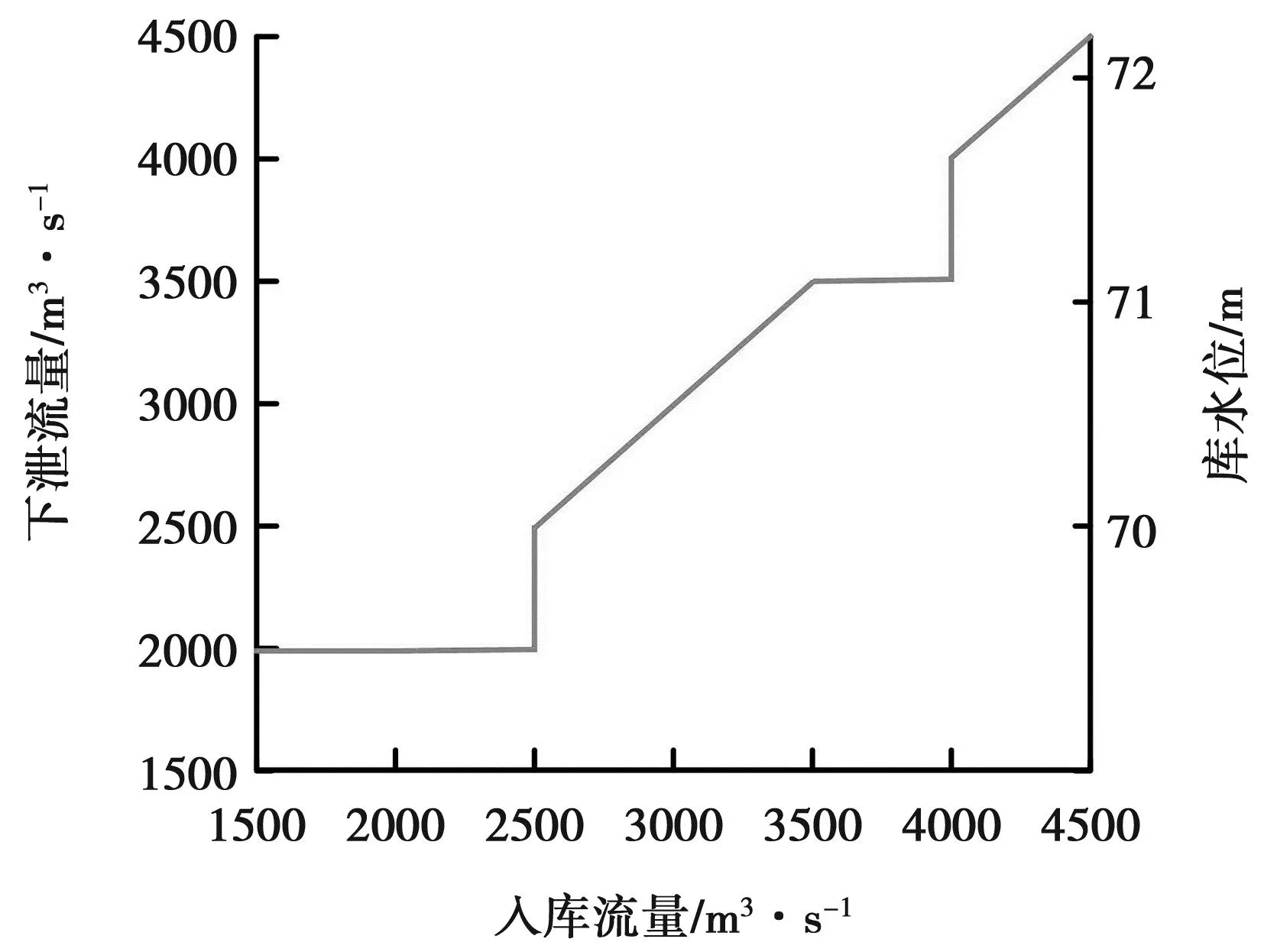
图4 峡山水库调度规则设置

图4中,水库的入库流量为2 000～2 500m3/s时,水位高度不高于70m,而下泄控制流量为2 000m3/s;水库的入库流量为2 500～3 000m3/s时,水位高度为70～71m,而下泄控制流量与入库流量相等;水库的入库流量为3 000～3 500m3/s时,水位高度为70～71m,而下泄控制流量与入库流量相等;水库的入库流量在3 500～4 000m3/s时,水位高度不低于71m,而下泄控制流量为3 500m3/s;水库的入库流量在4 000m3/s以上时,水位高度不低于71m,而下泄控制流量与入库流量相等。

根据图4的调度规则,得到不同频率洪水条件下水库水位的调节结果,见图5。

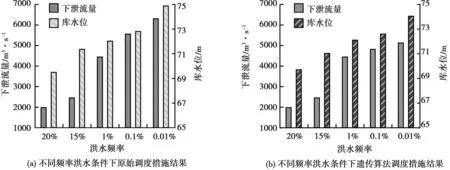
图5 不同频率的洪水条件下水库水位调节结果

图5(a)中,原调度措施在20%的频率中,水库水位高度69.5m,下泄流量2 000m3/s;15%的频率中,水库水位高度71.4m,下泄流量2 500m3/s;1%的频率中,水库水位高度72.1m,下泄流量4 500m3/s;0.1%的频率中,水库水位高度72.9m,下泄流量5 500m3/s;0.01%的频率中,水库水位高度74.9m,下泄流量6 300m3/s。

图5(b)中,改进遗传算法的调度措施在20%的频率中,水库水位高度69.7m,下泄流量2 000m3/s;15%的频率中,水库水位高度71.0m,下泄流量2 500m3/s;1%的频率中,水库水位高度72.0m,下泄流量4 450m3/s;0.1%的频率中,水库水位高度72.7m,下泄流量4 800m3/s;0.01%的频率中,水库水位高度74.2m,下泄流量5 100m3/s。

数据结果显示,洪水频率较大的条件中,两种调度方式在下泄流量中相同,但遗传算法的调度措施占用的库容更小;在洪水频率较小的条件中,采用遗传算法的调度措施,水库下泄流量更低,表明遗传算法的汛限水位与调度措施更有利于水库自身与下游地区的防洪安全。

试验进一步验证模型性能,通过水库发电效益进行评估,其效益结果见图6。

图6 基于遗传算法的水位控制效益评估结果

由图6可知,在洪水频率为0.01%的条件下,遗传算法的汛限水位与原水位相比上涨0.7m;从水库的总库容分析,总库容增加2 947m3;从发电库容分析,发电库容增加1 400×104m3。根据峡山水库单位电能耗水量的平均值进行计算,遗传算法的汛限水位可增加233.33×104kW·h的发电量。结果表明,遗传算法的汛限水位可使水库获得更多的蓄水量与发电效益。

2.2 改进遗传算法的性能分析

通过增加不同算法的对比,进一步验证改进遗传算法性能,其中包括标准遗传算法、粒子群算法、免疫算法、人工神经网络。试验模型通过Schaffer测试函数,对收敛度、收敛代数与模型运行时间3项指标进行对比,且试验对5种算法分别进行30次测试。不同算法在测试函数中的性能结果见图7。

图7(a)中,标准遗传算法的平均收敛值为0.980;粒子群算法的平均收敛值为0.981;免疫算法的平均收敛值为0.983;人工神经网络的平均收敛值为0.978;改进遗传算法的平均收敛值为0.993。图7(b)中,标准遗传算法的平均收敛代数为107.6次;粒子群算法的平均收敛代数为64.3次;免疫算法的平均收代数为52.7次;人工神经网络的平均收敛代数为73.3次;改进遗传算法的平均收敛代数为36.0次。试验中,改进遗传算法在测试函数里的性能表现最佳。该算法的平均收敛值与平均收敛代数均明显优于其他算法,表明改进遗传算法跳出局部最优解的能力较强。

图8为不同算法在模型中运行效率对比。图8中,标准遗传算法在迭代50次左右时,其运行时间逐渐稳定,最终运行时间稳定在53ms;粒子群优化算法在迭代40次左右时,其运行时间曲线开始收敛,最终稳定在45ms;免疫算法与粒子群算法相比,运行时间曲线均在迭代40次左右开始收敛,但其运行时间最终稳定在40ms;人工神经网络在迭代45次左右时,运行时间曲线开始收敛,并最终稳定在47ms左右;改进遗传算法在迭代30次左右,运行时间曲线开始收敛,并最终稳定在30ms。试验中,改进遗传算法在运行效率上具有明显优势,表明该算法能更快对问题进行分析,满足控制系统的实时性。

3 结 论

汛限水位是水库防洪效益与发电效益相冲突的因素,对汛限水位进行动态调整,对防洪与发电均有重要作用。因此,研究采用遗传算法,并对算法进行改进,以满足汛限水位的动态调整。在实例试验中,该算法根据不同的洪水频率以及入库流量,对汛限水位进行调整,与原始汛限水位相比提升了0.7m,增加了2 947m3的蓄水量。结果表明,研究建立的水库汛限水位动态控制模型,充分考虑了防洪库容的补偿性,对汛限水位实现了实时性控制。但在效益分析中,未充分考虑弃水量因素。因此,后续研究应充分考虑汛限水位调整的效益冲突,进一步提升汛期水位控制的科学性与安全性。