基于数值模拟的低水头闸坝工程下游冲刷动力研究

薛玉山,郭 萍

(安徽省亳州市谯城区水利局,安徽 亳州 236800)

0 引 言

水坝下游冲刷问题是指由于闸坝的建设,导致下泄水流具有较高的流速,从而造成下游床面及两岸边坡的严重冲刷破坏[1]。这种冲刷现象可能造成岩石与岸坡侵蚀和冲刷、河床变浅并形成淤积,以及对水质与生态的影响[2]。这种冲刷现象不仅影响尾水出流和通航能力,还会危及闸坝自身以及下游流域的安全[3]。因此,研究低水头闸坝工程下游冲刷问题,具有重要的价值和意义。

目前,传统试验和现场实测主要依靠试验数据来预测冲刷深度,但由于各工程具有特定的条件以及试验的局限性,上述方法在预测和分析方面仍然存在一定的不足。近年来,随着相关流体运算技术的发展,数值模拟已经成为冲刷问题研究的首选方案。基于先进的计算机模拟技术,可以准确描述闸坝下游水流的力学行为,并得出相应的结论。

因此,为了有效分析低水头闸坝工程下游冲刷造成的影响,本文通过结合试验分析与数值模拟的方法,对不同工况下的低水头闸坝冲刷问题进行研究,以获得对闸坝下游局部冲刷问题的深入认识和准确描述,为相关工程的设计和建设提供科学依据,从而推动水利工程的可持续发展。

1 基于数值模拟的低水头闸坝工程下游冲刷动力分析

1.1 低水头闸坝水工模型试验分析

研究以安徽省某低水头闸坝工程为试验研究对象。为了有效地对低水头闸坝工程下游冲刷影响进行分析,采用重力相似准则设计水工模。水工模型包含供水系统、闸室、上下游河道等部分,工程中墩左右设有两个半孔泄洪闸。整个模型按照1∶50几何比构建,设置流速比尺为1∶17 634。整个建模长度20m,在闸室下游底板5m区域属于动床范围,设置各种工况均沙,下游部分设置为定床。整个闸室剖面结构见图1。

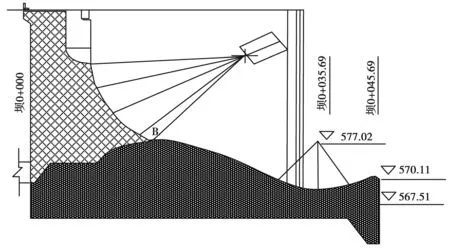
图1 闸室剖面图

整个水工建模中,为了尽可能反映出工程实际面临的各种工况冲刷问题,需要选取不同大小的砂石颗粒,以模拟自然环境对工程冲刷的影响。通过人工筛选,选出粒径为10、6、2mm的纯天然且无黏性的泥沙,并且所有砂石均取自工程场景。为了尽可能模拟工程实际冲刷效果,试验中需要用到各种仪器设备辅助实现,包括水准仪、测针、水准尺、钢板尺、声学多普勒流速仪以及声学设备专用测架等[4],并记录相关数据。试验中采用的是小威龙测流仪,相较于传统设备,其原理是通过声波信号折返,获取水流三维瞬间流速值,且反应速度、效率更快,能更准确记录水流流速情况。

在试验数据记录中,利用声波信号采集水流数据,难免会受到环境因素影响,导致记录数据误差偏大。为了降低采集数据误差,对流速仪采集多个信号进行优化,通过信噪比与相关系数值对数据进行判断,并保留主要数据,从而提高流速仪采集数据的精准性。其中,定义信号值大于15dB、相关系数值在60%～100%的数据将被保留。

整个水工模型构建中,通过3种不同工况冲刷试验来反映冲刷对工程的影响,并记录每个工况下冲刷坑深度以及冲刷过程水流状况[5]。具体水工模型试验如下:在搭建的水工模型上,以0.05、0.10及0.15m3/s共3工况进行下泄比较实现。3种工况对应实际工况参数分别为880、1 760及2 640m3/s。同时,选取3种不同规格的泥沙作为冲刷材料,规格分别为10、6、2mm,其对应原有砂石规格为500、300及100mm。通过不同工况环境的试验,测试冲刷对闸坝下游局部的影响,并在冲刷的过程中对冲刷坑深度以及冲刷后坑型进行数据检测,从而探究不同工况冲刷对闸坝工程的影响。选取其中一个工况,该工况为床沙粒径6mm,下泄流量0.05m3/s,当下游局部冲刷达到一个极限稳定冲刷状态时,利用超声波多普勒流速仪,对冲刷坑上部瞬时流速进行检测,并多次检测瞬时流速,将测试的数据进行整理,从而获得冲刷坑上方流场的分布情况[6]。

在床沙粒径6mm、模型设置的泄流量为0.05m3/s工况中,筛选出需要规格的砂石材料,并在水工模型下游部位将选好规格的砂石进行均匀摊铺,要保证摊铺平整,同时与砂石尾坎末端齐平,并通过水准仪进行检测校核[7]。然后开闸调节水流量,在调节水流量参数时,需要对水工模型下游动床部分设置隔水板,防止调整水流量对床面形态造成影响。当水量参数为标准值时,即可撤除隔水板,并进行下游动床冲刷。在动床冲刷中,需要定时对水槽轴面最大冲刷深度进行检测。当检查冲刷深度保持不变时,可以认定此时已经达到冲刷最大深度状态,床面状态基本维持一种稳定形态,采用流速仪对冲刷坑上部轴面三维流速进行检测与采集,设备采集频率参数设置为100Hz,每个采集点采集时间设置为60s。通过模型试验,记录不同工况冲刷的流量及湍动强度,从而评价不同工况冲刷对工程的影响。

1.2 数值模拟模型的构建

为了进一步分析闸坝工程下游冲刷情况,研究采用Fluent系统进行数值模拟分析。目前,对于明渠水流热能变化研究较少,能量守恒不满足研究要求。而且研究的冲刷主要为湍流类型,该类型属于非线性运动,进行数值求解需要选择合适的湍流模型[8]。因此,在构建闸坝工程下游冲刷数值模拟模型时,选取合适的湍流模型以及数值计算方法。其中,水流冲刷需要满足牛顿流体运动要求,采用流体连续运动与纳维叶-斯托克斯方程(Navier-Stokes,N-S)描述流体运动。

连续运动表达式如下[9]:

(1)

式中:ρ为流体密度,kg/m3;u、v、w分别为X、Y、Z方向的流速分量。

N-S动量方程如下:

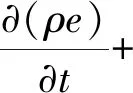
(2)

式中:u为流体速度矢量;p为压力,kPa;e为单位质量的总能量,J;g为重力加速度;κ为热传导率;T为温度,℃;τ为应力张量,Pa。

然后需要选择有效的湍流模型。直接数值模拟方法理论上能够对连续性流体运动进行求解,但实际计算中需要大量的参数与运算量,且对于该类工程问题求解较困难。近年来,随着计算机技术不断发展,计算机数值模拟技术是目前解决工程实际问题的首先方案。其中,在解决湍流问题上Reynolds平均法有着非常广泛的应用[10]。Reynolds法主要是对时均Reynolds方程进行求解,从而实现对N-S方程的闭合。

因此,研究采用Reynolds平均法作为湍流模型,通过Reynolds平均法构建与雷诺应力相关的函数,从而实现对N-S方程的封闭,避开雷诺应力计算得到解析解;当求解湍流黏度时,求解值为两数时为两方程模型。常见的两种方程模型有Standardk-ε模型与RNGk-ε模型。综合比较而言,后者对湍动黏度问题有更好的适应性。同时,RNGk-ε模型添加了表征主流时均应变的项,可以很好地对弯曲流线问题进行计算。因此,选择RNGk-ε模型解决湍流计算问题。但RNGk-ε模型仍需要采用壁面函数法,解决近壁面区域计算问题[11]。RNGk-ε模型表达如下:

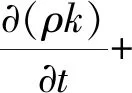
(3)

式中:k为湍动动能,m2/s2;ε为湍动耗散率;μ为动力黏度;G为源项;C1、C2为经验系数。

在数值模拟中,需要设置合适的边界条件参数,以满足整个数值模拟的精度要求,边界条件参数值将影响整个数值模拟的精度与收敛效果。其中,常见边界类型特征见表1。

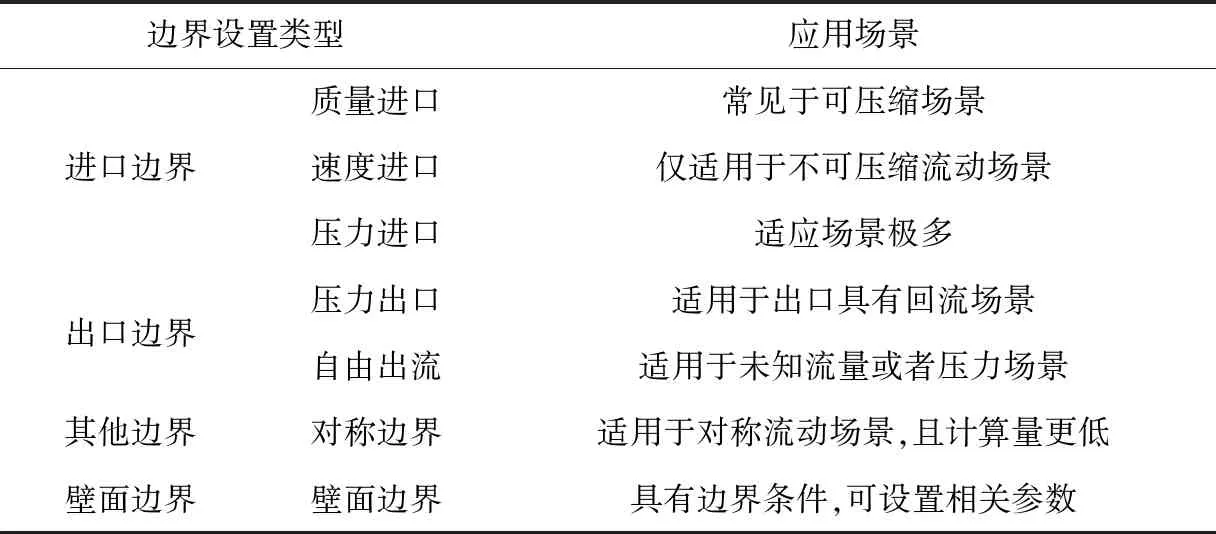
表1 Fluent平台常见边界类型特征

对于明渠相关的研究问题,通常选择速度入口或压力入口,出口可以选择自由流出或压力出口。在数值模拟中,还需要对计算机性能进行考虑,设置一定范围的网格数。由于数值模拟中闸室长度并不能完全满足流动发展要求,因此模拟中选择压力出口即可。同时,工程属于低水头大流量闸坝项目,选择Standard Wall Functions函数对近壁进行优化处理。此外,考虑在数值模拟中流体随时间突变现象,采用动网格技术进行优化,通过引入动网格的宏函数控制流体突变问题,从而提高运动物体模拟效果[12]。

2 水工模型冲刷试验分析

2.1 工程概况

选择安徽省某水电站工程为试验对象,项目控制流域面积18 652km2,工程总库容2 856×104m3。该工程主要为发电项目,工程建筑包含泄洪闸、挡水坝、发电厂房等。整个项目属于常规的河床式电站,整个项目中设置3台水轮机,装机容量36 000kW。工程大坝高度38m,坝顶高程560m。副坝段挡水建筑属于常规的混凝土重力坝,采用闸坝泄水形式,泄水闸段宽度86m。图2为水电工程平面布置图。

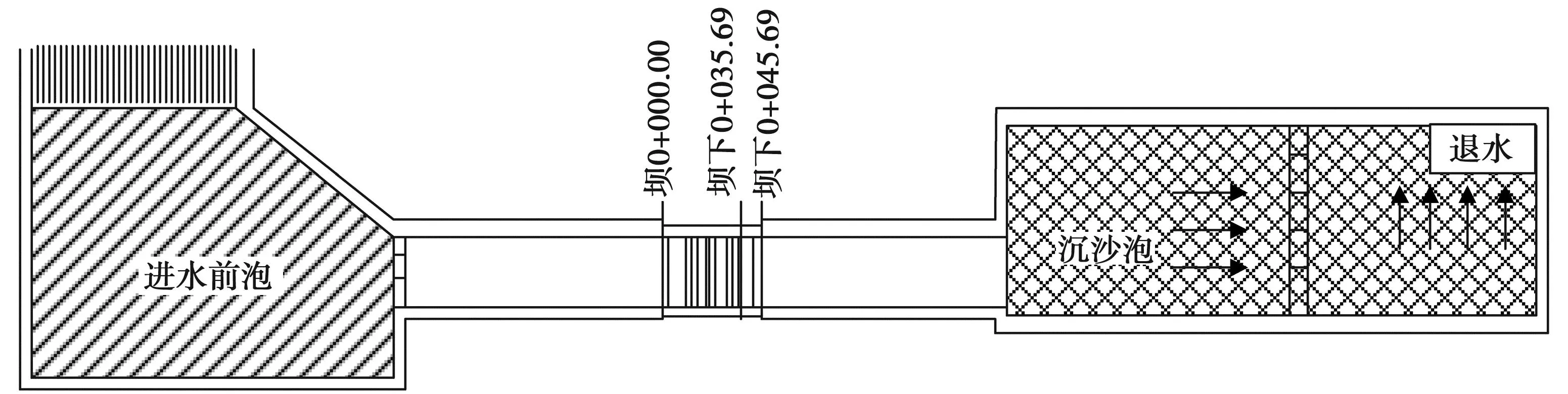
图2 某水电工程平面布置图

2.2 冲刷试验分析

为了有效分析工程冲刷情况,将设置专门的放水工况,从而更真实地模拟实际冲刷影响。其中,第一组设置模型流量0.05m3/s,模型粒径10mm;第二组设置模型流量0.05m3/s,模型粒径6mm;第三组设置模型流量0.05m3/s,模型粒径2mm;第四组设置模型流量0.10m3/s,模型粒径10mm;第五组设置模型流量0.15m3/s,模型粒径10mm。分别对5种工况进行水工模型试验,结果见表2。

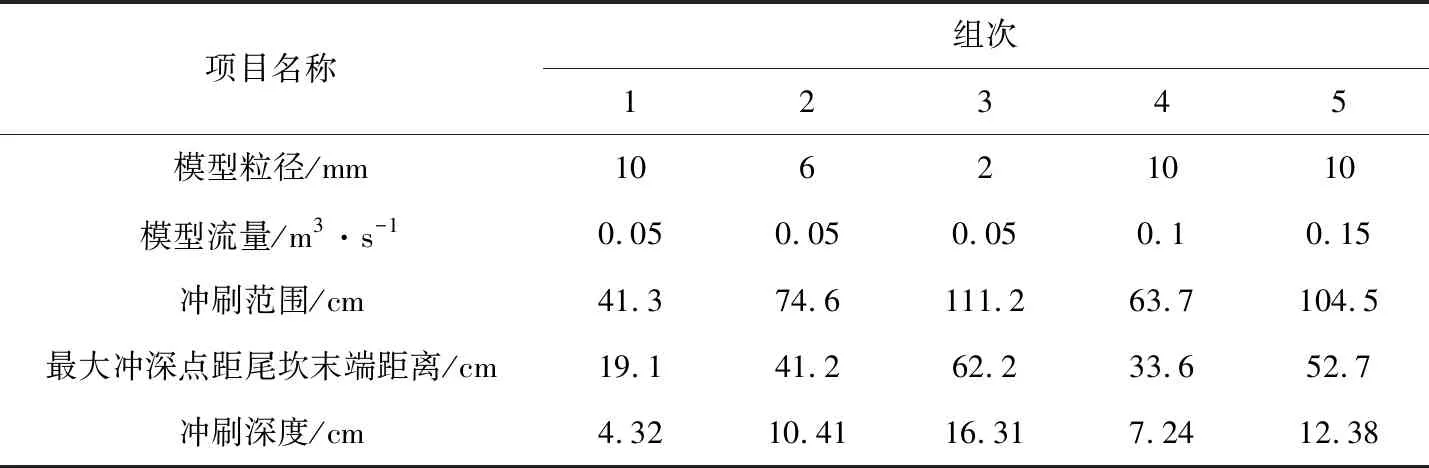
表2 水工模型冲刷试验结果

由表2可知,水工模型下游冲刷基本以两边以及中间深分布展开。在试验检测中,床面最深点位于边壁周围,其原因是水流冲刷会在边壁附近出现二次水流冲刷现象。5组工况测试显示,相同模型流量下,粒径为2mm时,冲刷的深度越大,冲刷深度为16.31mm。表明在流量一致时,粒径越小,冲刷深度越大。同时,对比相同模型粒径的工况1、工况4以及工况5,当流量为0.15m3/s时,冲刷坑深度越大,此时冲刷坑为12.38m。表明粒径一样时,流量越大,冲刷坑越大。

对工况2场景进行分析,根据X、Y、Z三个方向绘制出冲刷坑上方流速分布情况,见图3。

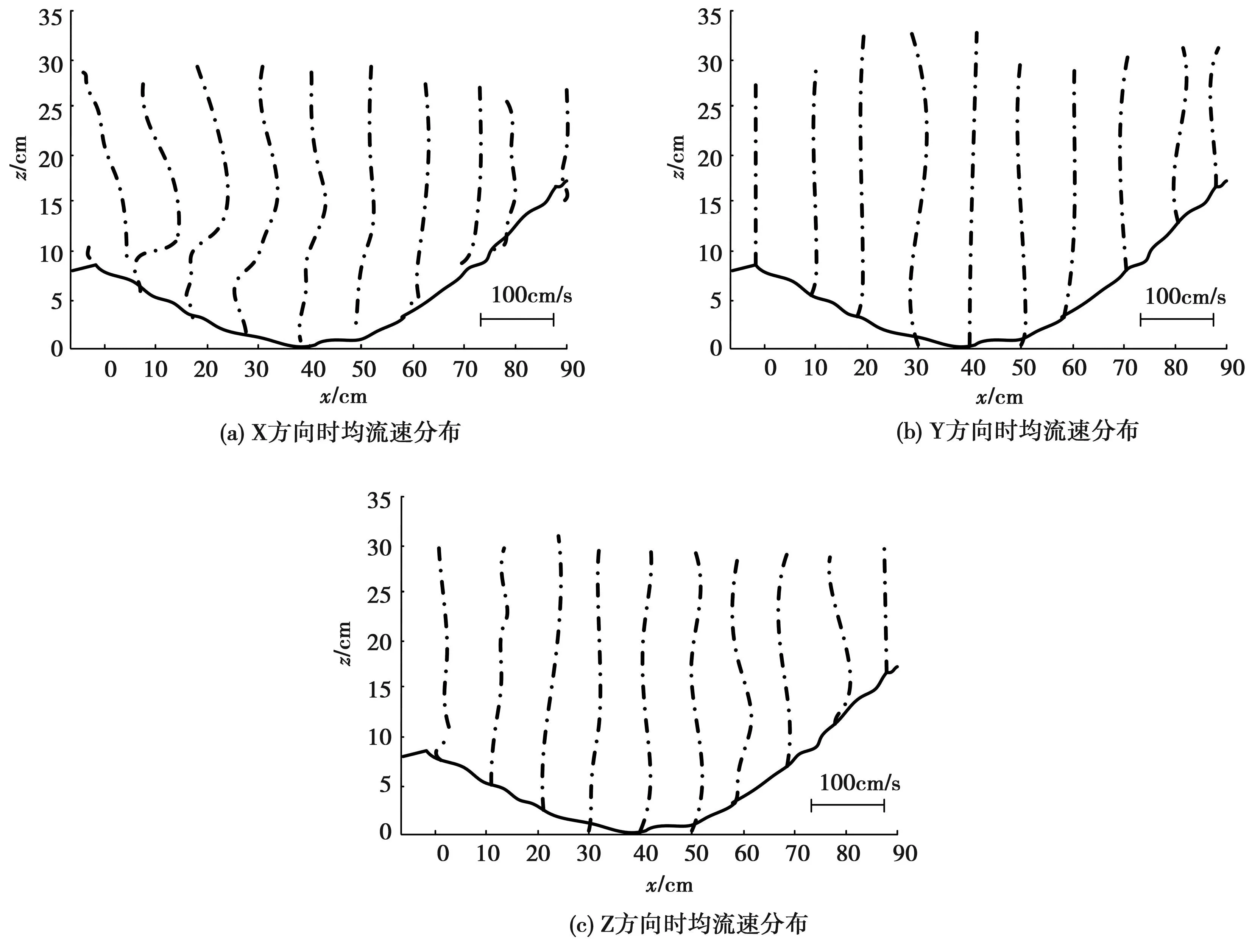
图3 冲刷坑上方流速分布

选择图3中最大冲刷坑分析流速分布情况。由结果来看,尾坎距离中间闸墩收窄位置最近,在尾坎末端5cm的X方向出现最大流量,流速为0.82m/s。由于尾坎存在朝上的挑角,此处Z轴向上区域流速为正。随着水流往下方流动,在尾坎抛出获得最高点并斜向冲刷坑,在Z方向分布中有体现。同时,水流离闸室越远,水流垂直越均匀,可由X方向分布看出。进一步分析发现,冲刷坑上游区域湍动的水流耗能最高,对冲刷坑有直接影响。

为了进一步分析低水头闸坝工程下游冲刷动力情况,将水工模型分析获取的数据进行数值模拟分析,检验所采用的Fluent系统是否满足闸坝冲刷坑模拟计算。依旧选择工况2场景进行数值分析,水面线比较见图4。

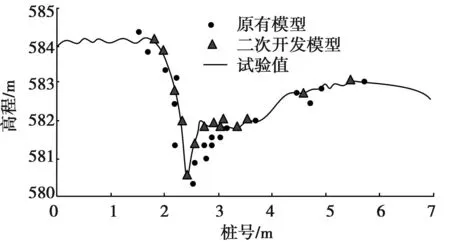
图4 沿程水面线数值模拟

图4中,分别对模拟值与试验值进行比较,其中选择积分数为0.5的等值面作为提取位置。结果表明,二次开发模型与试验检测数值基本拟合。水流下泄经过2号桩时,出现明显的水位下跌情况,最低数值为581.65m,二次开发模型与实际值基本吻合;传统Fluent模型对水位下跌的拟合较差,二次开发模型相对误差为0.096%,原有模型为0.566%,表明二次开发模型更适应对实际冲刷面的分析。同时,对泄流量也进行了模拟,二次开发模型与实际值基本吻合,误差范围在0.08%～0.32之间,满足最大误差4%要求。

对冲刷坑流速分布进行数值模拟,见图5。

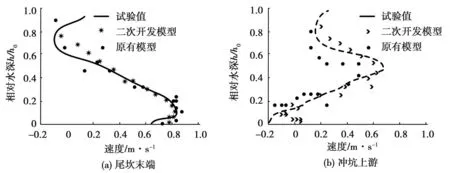
图5 冲刷坑流速分布数值模拟

图5中,选取尾坎末端与冲刷坑上游进行模拟,二次开发模拟获得分布值与试验实际测量结果基本一致。在尾坎末端流速分布中,尾坎末端相对水深0.1m时,流速值最大,最大流速值0.8m/s,模拟值与实测值基本一致,误差0.092%,符合预测要求;原有模型误差较大,为4.658%,无法满足要求。同时,冲刷坑上游存在回流现象,二次开发模型也能准确识别,优于原有模型,可为低水头闸坝工程维护提供重要数据参考。

3 结 语

本文针对低水头闸坝下游河床冲刷问题进行了有效分析,以某水电工程为研究对象,构建水工模型。同时,以Fluent平台数值模型为基础,通过壁面函数法,解决了近壁面区域计算问题,并引入动网格,实现了对数值模型的优化。结果表明,在水工模型试验中,当模型流量最大、模型粒径最小时,下游冲刷范围以及冲刷坑深度就越大。在数值模拟分析中,二次开发模型能准确反映水面实际值,与试验值接近。在流速分布数值分析中,二次开发模型相对误差为0.092%,优于原有模型的4.658%。鉴于水流与泥沙位置的随机性,未来还需要考虑粒径运动特点,以提高模型分析效果。