基于国产加速器URT-Linac 506c的计划复杂度分析和患者计划质量保证预测

祝鹤龄，杨波，祝起禛，梁永广，杨景茹，王贝，王嘉欣，邱杰

中国医学科学院北京协和医院 放射治疗科，北京 100730

引言

随着放射治疗技术的进步，作为一种新型放疗技术，调强放射治疗（Intensity Modulated Radiotherapy，IMRT）逐渐取代三维适形放射治疗技术（Three Dimensional Conformal Radiation Therapy，3DCRT） 广泛应用于临床。IMRT 通过借助限束设备对射束强度进行调节，使放疗靶区处的三维剂量分布具有更好的适形性，同时进一步规避周边正常组织的照射。但是与3DCRT 相比，新型放射治疗技术在达到更理想剂量分布的同时，无疑会使治疗计划的复杂程度上升[1]。治疗计划的复杂性通常被认为是治疗计划剂量计算和实际执行时各种因素导致的剂量不确定性的量化估计，与形成治疗计划所涉及的各种参数相关[2]。为了保证临床可接受的剂量分布，一定程度的计划复杂性是可以接受的，但是过于复杂的治疗计划理论上会加剧治疗计划设计系统优化得到的剂量分布和计划实际执行时剂量分布的偏差，从而在一定程度上影响放疗计划在临床应用中的稳定性和可靠性[3]。因此在治疗实施前，往往需要对患者计划质量保证（Patient Specific Quality Assurance，PSQA）进行检验，以确保用于执行的放疗计划准确可靠。

PSQA 是放射治疗工作流程中必不可少的步骤，用于验证可能受到剂量计算、数据传输、直线加速器输送性能等因素影响的放疗计划在执行过程中的可靠性[4-6]。一般是在放疗计划完成之后，利用计划验证系统将基于人体设计的治疗计划移植到测量模体上，生成相对应的验证计划，随后用医用直线加速器采集实际投照到测量模体上的剂量信息，通过对比该验证计划的实际剂量分布和模拟得到的剂量结果，判断二者的差异以评估治疗计划的优劣。然而大量的验证工作对工作量较大的放疗中心来说是一个严峻的挑战，因此，研究计划复杂度参数与PSQA 间的关系，寻找一种更为精密、自动化、低资源密度的PSQA 反馈方法尤为重要。

目前已有多项研究使用人工智能技术基于治疗计划的各项复杂度参数指标对PSQA 结果进行预测分析。Valdes 等[7-8]使用泊松回归和Lasso 正则化建立了一个线性模型，以基于治疗计划的复杂性参数预测计划的伽马通过率结果。Lam 等[9]使用了3 种基于梯度提升决策树（Gradient Boosting Decision Tree，GBDT）模型的算法来预测美国瓦里安公司的TrueBeam 和Trilogy 加速器的PSQA 验证结果。Granville 等[10]使用支持向量机算法根据计划复杂性指标和加速器性能参数对不同类型的计划进行分类。国内有部分研究基于瑞典医科达Infinity及Synergy 加速器对应的放疗计划软件进行了剂量验证相关研究[11-12]，然而基于国产加速器联影URT-Linac 506c 的放疗计划复杂度在业界还未被研究。

本文探讨基于URT-Linac 506c 的容积弧形调强放射治疗（Volumetric Modulated Arc Therapy，VMAT）计划的各项复杂度参数与PSQA 结果间的相关性，并基于复杂度指标搭建机器学习模型，对PSQA 结果进行预测，对各项计划复杂度在模型评估中的重要性进行分析。

1 资料与方法

1.1 一般资料

随机选取北京协和医院放疗科2022 年8 月至2023年4 月使用国产联影URT-Linac 506c 加速器治疗的VMAT 计划中的150 例患者进行回顾性分析。计划设计系统均使用联影URT-Linac 506c 计划系统，剂量计算采用坍缩锥卷积叠加算法[13]。

1.2 计划验证

患者治疗前，将计划移植于机载电子射野影像装置（Electronic Portal Imaging Device，EPID）探测器，在联影URT-Linac 506c 加速器上进行计划验证（以下简称EPID-pre）。对比EPID 采集的二维剂量和计划系统移植剂量分布，基于联影URT-Linac 506c 计划系统分析计划的伽马通过率[14]。所有伽马分析指标均按照2 mm/2%的标准和10%的最大剂量阈值进行评价。

1.3 复杂度参数

基于先前在瓦里安Halcyon、TrueBeam 加速器上的已有研究[15-16]和物理师的经验，本研究团队提出了11 个不同的复杂度参数反映计划复杂程度的不同层面。从URT-Linac 506c 计划系统中导出DICOM 格式的治疗计划文件，使用Python 脚本计算11 个计划复杂度参数，包括波束孔径的大小和不规则性、控制点开野面积和周长等与多叶准直器（Multi Leaf Collimator，MLC）位置的相关参数和计划跳数。VMAT 计划机架每旋转2°为一个控制点，先计算每个控制点的复杂度参数，后根据各控制点跳数加权求和得到计划的总复杂度。对于URTLinac 506c 加速器，仅在坞门打开范围内的有效MLC位置参与计算。9 类共11 个复杂度参数的具体定义和计算方式如下。

（1）平均子野面积变化率（Aperture Area Variability，AAV）[17]：每个控制点上的AAV 计算方法如公式（1）所示。

式中，posa为第a对MLC 叶片的位置坐标；A为MLC 叶片对的总数目；下标leftbank 为左侧铅盒储存的MLC；下标rightbank 为右侧铅盒储存的MLC。AAV 是将每个控制点的子野面积归一化到所有子野叠加面积上后，基于控制点的跳数取加权平均，其取值范围为0～1，值越小，计划越复杂。

（2）平均子野面积（Beam Area，BA）[18]：BA 为每个控制点上MLC 打开子野面积的加权平均数，计算方法如公式（2）所示。

式中，AAcp为第cp个控制点的子野面积；MUcp为该控制点的机器跳数；MUall为计划总跳数。子野面积越小，计划越复杂。

（3）周长/面积比（Circumference Area，CA）[19]：CA 为每个控制点上MLC 叶片形成的子野周长与面积的比值，再基于控制点的跳数取加权平均。CA 越大，计划越复杂。

（4） 平均叶片序列变化率（Leaf Sequence Variability，LSV)[17]：LSV 为在每个控制点上，相邻MLC 之间的位置差异相对于该控制点中的最大位置变化，计算方法如公式（3）所示。

式中，posa为第a对MLC 叶片的位置坐标；posmax为该控制点中MLC 的最大位置差；A为MLC 叶片对的总数目；下标leftbank 为左侧铅盒储存的MLC；下标rightbank 为右侧铅盒储存的MLC。LSV 越小，子野形状越不规则，计划越复杂。

（5）平均不对称距离（Mean Asymmetry Distance，MAD）[20]：MAD 为每个开放的叶片对中心与中心光束轴间距离的平均值。

（6）调制复杂度分数（Modulation Complex Score，MCS）[17]：MCS 为相邻控制点间的LSV 和AAV 平均值的乘积。

（7）联合子野面积（Union Aperture Areas，UAA）[18]：UAA 为各控制点所有孔径叠加得到的最大孔径面积。

（8）小孔径分数（Small Aperture Score，SAS）[20]：SAS 为孔径距离小于X 的MLC 对 占总有效叶片对的比例。本研究中计算了X=5、10、15 mm 情况下的SAS参数值（SAS5、SAS10、SAS15）。SAS 越大，计划中用于调制的小孔径数量越多，计划越复杂。

（9）计划跳数（Monitor Unit，MU）[18]。

1.4 建模与数据分析

计算各复杂度参数与EPID-pre 的通过率间的皮尔逊线性相关系数，分析二者的线性相关程度，同时通过2 种不同的决策树模型，即GBDT 模型[21]和随机森林（Random Forest，RF）模型[22]，学习复杂性参数和EPIDpre 通过率之间的深层关系，并给出预测结果。本研究中的所有统计数据均采用Python 3.8 软件进行分析，并使用基于Python 的sciki-learn 工具包搭建机器学习模型。

2 结果

2.1 线性相关性检验

11 个相关的复杂度参数与计划PSQA 通过率间的对应关系如图1 所示。其中SAS、CA 与伽马通过率间表现出了较明显的负相关，LSV 与伽马通过率则表现出较明显的正相关。理论上，计划越复杂，SAS 和CA 越高，而LSV 越低，伽马通过率通常越低，故该结论与上述各复杂度参数的定义相符，但复杂度参数与计划复杂程度、伽马通过率间的关系复杂，并不一定严格符合线性关系。

2.2 机器学习模型

本研究搭建了2 种基于决策树结构的机器学习模型以进一步研究复杂度参数与计划伽马通过率之间的关系，即GBDT 模型和RF 模型。研究使用的150 例数据被随机分成训练集和测试集。在训练集中，共105 例（70%）计划数据被用于训练模型的搭建和模型性能的探索。为了避免决策树结构的过度拟合，首先对模型调参阶段进行了10 倍交叉验证[23]，以优化模型的超参数，包括估计器的数量、叶节点所需的最小样本数量和每个决策树的最大深度等。在测试集中，额外45 例（30%）独立测试计划被用于进一步评估不同模型的性能。根据各数据集在各个通过率区间的分布可知，基于通过率的样本通常是非常不平衡的，仅有约5%的样本具有相对较低的通过率测量值，导致常规机器学习模型对低通过率区间的样本预测误差相对较大，见表1。

表1 数据的伽马通过率在各区间分布[n（%）]

为了解决这一问题，在模型训练阶段，根据每个宽度为1%的伽马通过率区间中的样本数量，对样本赋予不同的权重，即小样本区间的每个训练样本拥有更大的权重，使得最终每个区间样本的总权重数相同。根据测试集在未更改权重和更改权重后的GBDT 模型和RF 模型中的平均预测误差可以看出，尽管总的误差有小幅度提高，但低通过率区间的误差显著降低了，见表2。

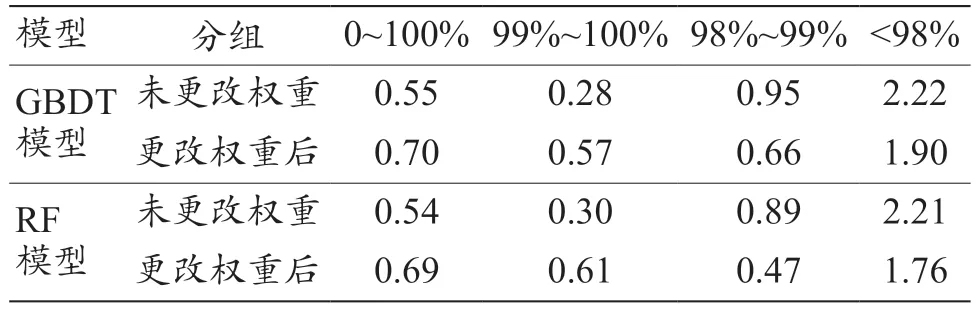
表2 不同伽马通过率区间下测试集数据的平均预测误差（%）

2.3 特征重要性分析

为了研究基于联影URT-Linac 506c 加速器MLC 叶片计算的不同复杂性度量对计划实际通过率的贡献，本研究进一步进行了基于模型的特征重要性分析。研究采用特征重要性排列序的方法[24]，通过随机打乱某个感兴趣复杂度参数的值观测模型预测结果的变化，通过模型预测误差的升高评估该特征变量的重要性。理论上，被打乱的特征越重要，模型预测误差就越大。在GBDT 模型和RF 模型中各复杂度参数的重要性如图2 所示，重要性数值越接近1 表示该复杂度参数越重要。在2 个模型中，用于预测的特征重要性不完全相同，但SAS、CA、MAD 等复杂度参数在2 个模型中均较为重要。

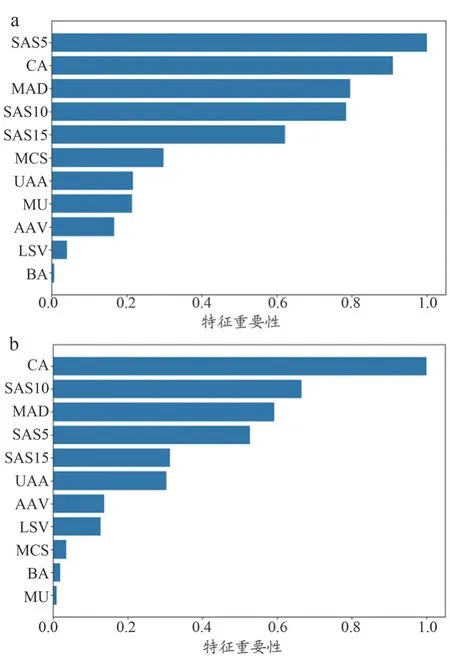
图2 各复杂度参数在机器学习模型中的重要程度排序图

3 讨论

多项研究表明，机器学习模型对PSQA 结果的预测有一定帮助，然而不同加速器MLC 叶片结构、长度、铅/坞门大小和机械运动模式会有一定差别。本文分析了国产加速器联影URT-Linac 506c 的计划复杂度参数与PSQA 的通过率间的关系，并为该加速器配备了2 种基于不同决策树算法的PSQA 预测模型。该模型使物理师专注于预测伽马通过率（Gamma Passing Rate，GPR）较低的一小部分治疗计划，减少了物理师的工作量，优化了物理师的工作流程，使得PSQA 过程更加高效。

本研究提出了11 个不同的复杂度参数以反映计划复杂程度的不同层面，及其与计划执行准确性、可靠性间的联系。一直以来，计划的复杂程度被认为与剂量递送的准确性相关，一个高度复杂的调强计划可能导致治疗交付中更大的剂量不确定和不准确[25]，所以许多早期的研究试图找到一种或几种量化指标来描述和评估计划的复杂程度，并在这些复杂程度和实际QA 结果之间建立直接的数学关系。例如，McNiven 等[26]在2010 年结合各种参数开发了MCS；Masi 等[27]和Agnew 等[28]研究了MCS 和GPR 之间的相关性。但是复杂度的量化本身是一个较为困难的问题，单个数学公式的度量可能并不全面，就如同本文分析了11 个参数指标与通过率结果之间的关系并非线性的。因此，随着计算机技术的发展，基于多参数的、集成学习的决策树模型可以较好地应用到该项研究中。

基于机器学习模型，通过计划复杂度参数的特征重要性研究表明，在联影URT-Linac 506c 加速器的MLC中，SAS、CA、MAD 等参数在模型预测中表现得较为重要。SAS 为小孔径参数，用于概括每对MLC 开出的孔径中小孔径数量的占比，小孔径数量越多，射野调制越复杂。CA 为每个控制点上MLC 构造的子野周长与面积的比值，描述了射束射野形状的不规则性，周长越大、面积越小的情况下，CA 越大，计划复杂程度越高。MAD 为MLC 叶片对的平均不对称距离，表征了MLC叶片对开出的孔径偏离射束中心轴的程度。结果表明，这些对模型有较大贡献的复杂度参数与常规的认知相符合：更复杂的计划通常涉及更小、更不规则的光束孔径和更大的光束强度调制。

在调强放射治疗时代，MLC 在波束的形成和调制方面发挥着至关重要的作用，可帮助计划实现可接受的剂量分布，影响治疗的质量和效率。一般来说，一个理想的MLC 应该具有以下特点：精确的叶片定位精度、小半影和更快的叶片运动速度[29-31]。基于该加速器的在线自适应平台也已在本中心投入临床使用，更高效、更精简的PSQA 模式对于在线的适应放射治疗显得更为重要。因此，基于复杂度参数研究的PSQA预测模型和在线计划结合将是提高工作效率和优化工作流程的有用工具。

4 结论

本研究基于国产加速器联影URT-Linac 506c，进行了放疗计划复杂度与PSQA 结果间的相关性研究。结果表明，复杂度参数与计划PSQA 结果间存在较强相关性，而基于决策树算法的机器学习模型可对PSQA 伽马通过率预测起到一定作用，帮助放疗物理师更好地识别PSQA 测量失败的患者计划，为进一步研究和改进计划提供参考。