基于应变楔理论的水平受荷桩横向变形计算★

贺华刚

(重庆工商职业学院,重庆 401520)

1 概述

关于水平受荷桩的理论计算,目前学术界大致有以下几种:弹性地基反力法(m法)、p-y曲线法(p-y曲线法)、应变楔形法(SW法)。弹性分析法由于土体弹性模量不容易确定,只能进行定性分析,实际工程应用不多。p-y曲线法虽然应用较多,但仍然存在较多不足之处:过多依赖经验参数,适用面较窄[1];为了计算方便,把桩土作用简化成一维离散的非线性弹簧模型,从而忽略土体的空间连续性[2-4];未能充分考虑桩体特征,忽略了桩顶约束环境、桩身截面形状和抗弯刚度的影响。应变楔理论,克服了p-y法的部分缺陷,不依赖经验参数与现场试验,充分考虑桩身特性及桩周土体的空间连续性,而且在应变楔模型分析方法中p-y曲线并不是唯一的,而是随着土和桩身性质的变化而变化。

2 应变楔理论

桩基在水平荷载作用下挤压桩前土体,应变楔子理论认为此时在桩前会形成空间立体应变楔,如图1所示。

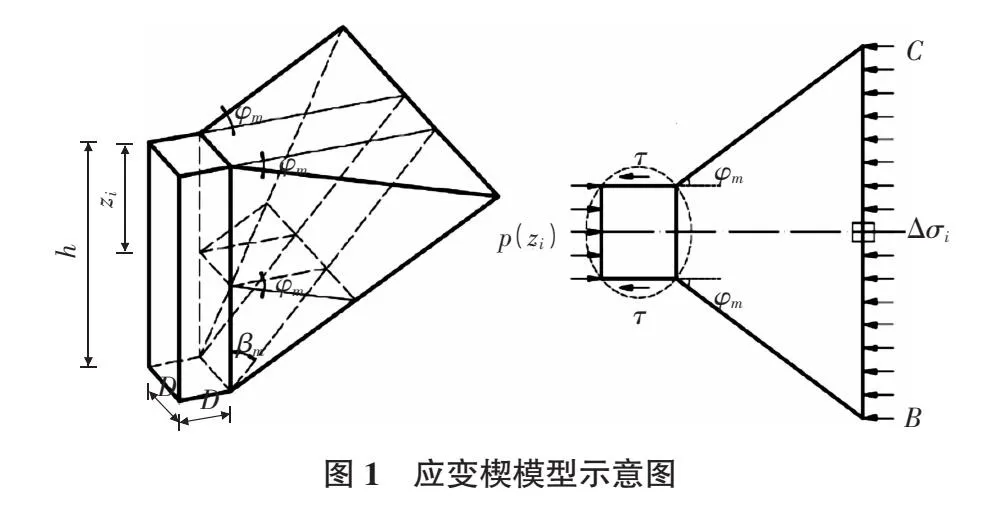
如图1所示,应变楔形土体模型通过以下基本参数描述[5]:应变楔形体的高度h,应变楔斜面的底角βm,水平方面的伞角φm(土体当前发挥的内摩擦角)。桩周土体由于桩的横向挤压会产生水平反力F和桩侧剪应力τ,不同深度土层由于水平位移不同,水平应力会发生变化(Δσh)。由于应变楔模型假设桩身水平位移在应变楔深度H范围内呈线性变化,因此桩身会发生线性化的偏转角δ。如此假设能确保土体中的应变在水平和竖向均匀分布。因楔形体的形状及大小、受力状态和桩身变形都会随着土体中的均匀应变而发生变化,当伞角φm增加至土的内摩擦角φ时,土体即发生剪切破坏。由于应变楔理论以砂土和黏土的有效应力分析作为基础,在黏土中应变楔的伞角φm并不为零。底角βm与伞角φm之间的关系为:βm=φm/2+45°。

基于该被动土楔的受力滑移,利用土体应变来分析和计算土的反应。单桩的水平特性尺寸效应随着桩径增加不断变大[6-7],而常用的弹性地基法不能考虑桩径尺寸效应带来的有利影响,导致计算结果过度保守。应变楔形模型既能考虑大直径单桩的尺寸效应影响,又能将三维楔形土体的应力、应变、强度与一维弹性地基梁联系在一起,在复杂的三维桩土相互作用和简单的一维弹性地基梁之间提供理论上的联系。

2.1 土地应力-应变关系

应变楔内土体的应力(σ)、应变(ε)和弹性模量等参数均来自等向固结排水三轴试验(砂土)或等向固结不排水三轴试验(黏土)[8-11]。水平应力增量Δσh可通过三轴试验中的竖向偏应力增量获得[12];与标准三轴试验中的围压不变相对应,则有应变楔形土体中,σv(竖向应力增量)=Δσh(垂直于水平方向的应力增量)=0;桩侧土体在水平横向荷载作用下,会产生一个沿桩身变位方向的水平应力增量Δσh与水平应变ε,土体弹性模量可表示为E=Δσh/ε,与三轴试验中的割线模量(偏应力与轴向应变关系曲线)相对应;水平有效应力与竖向有效应力满足关系:σh0=Kσv0,其中,K为侧向压力系数,取值为1(考虑沉桩效应),应变楔内土体的竖向有效应力σv0对应三轴试验中的均匀围压;竖向应变εv、与桩水平变位方向垂直的应变εph满足:εv=εph=-vε(v:土体泊松比)。因此,由应变楔内土体的应变莫尔圆可得:

(1)

其中,γ为剪切应变。

将应变楔土体在水平方向分为若干层,分析各层土体受力状态,如图2所示。

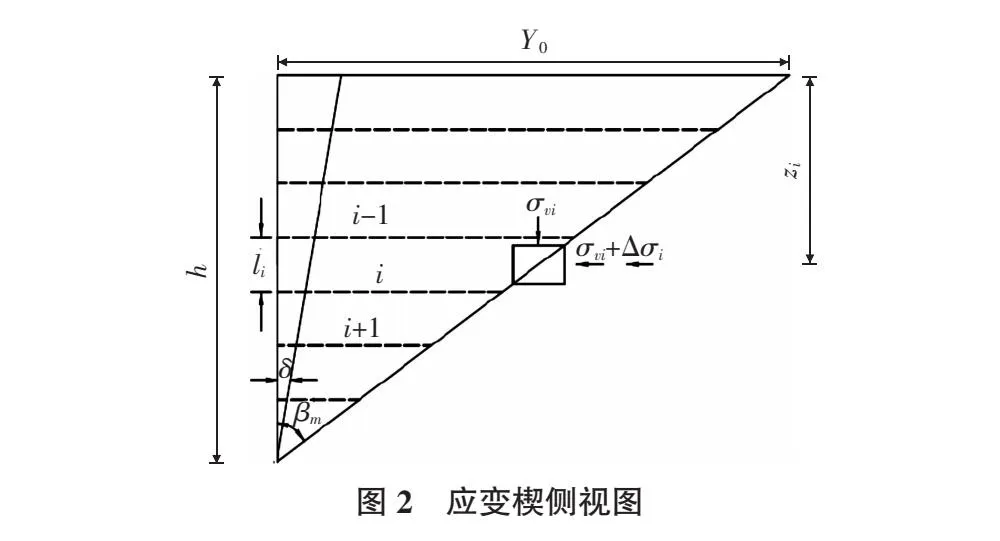
图2中y0表示应变楔在水平方向上的影响长度;li表示第i层土层厚度;σvi为竖向有效应力;Δσi为第i层土层的平均应力增量,沿垂直于荷载方向均匀分布。通过图1,由几何关系,可得应变楔底面宽度LiBC满足式(2):

LiB=D+2(h-zi)tanβmtanφm

(2)

同时考虑图2中各层土体的受力平衡,可知应变楔内任意土层均满足式(3)的平衡方程。

P(y,z)=ΔσiLiBCS1+2τDS2

(3)

其中,S1和S2为桩形系数(不同形状的桩,桩后土体受力情况会有所差异,方桩:S1=1;圆桩:S1=0.75,S2=0.5)。显然,式(3)中,除应力增量Δσi之外的其余参数均可确定,故合理求解Δσi的关键环节是合理确定地基水平抗力。

2.2 水平应力水平SL

地基水平抗力较为复杂,Ashour等[13]引入应力水平SL描述砂土、饱和黏土及一般黏性土的应力应变关系,以便能合理确定地基水平抗力。根据应力的莫尔圆,应力水平SL、伞角φm与Δσi的关系可表示为式(4),式(5):

(4)

Δσhf=σv0[tan2(45°+φ/2)-1]

(5)

基于各向同性固结排水和不排水三轴试验,定义土体应力水平与应变的关系如图3所示。

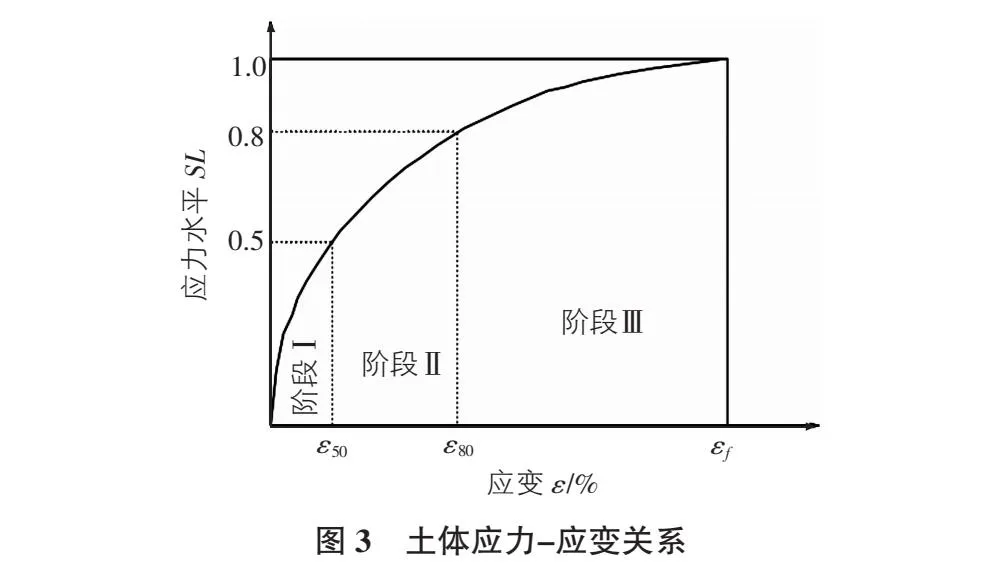
为方便计算,将图3中的曲线划分为三个阶段:ε≤ε50,ε50≤ε≤ε80,ε80≤ε,(ε50,ε80分别为达到极限应力水平50%和80%时所对应的应变),并用幂函数近似模拟三个阶段[14]。

1)当ε≤ε50,此时桩的水平荷载较小,桩前应变楔内土体产生的应力和应变较小,通过模拟,应力水平SL可表示为:

(6)

其中,系数3.707和3.19为修正系数。

2)ε50≤ε≤ε80,应力水平可表示为:

(7)

式(7)中,λi从3.19(SL=0.5)至2.14(SL=0.8)呈线性变化。

3)ε80≤ε,随着应力不断增加,当应力达到极限应力水平80%时,应力水平发挥至最终阶段,应力水平SL可表示为式(8):

(8)

其中,m取值59.0;qi=95.4ε50。

由上可知,应变楔中各层土体的地基反力模量Ei与其应力水平σ和应变ε满足:Ei=(Δσh)i/εi=SLi(Δσhf)i/εi,每层土体的弹性模量都可以通过迭代法依次解得。

2.3 桩侧剪应力τ分析

1)砂性土:砂性土中,桩侧剪应力表现为滑动摩擦力,可按式(9)计算:

τi(σvo)itanφsi

(9)

2)黏性土:黏性土中桩侧剪应力水平SLτ,可根据Coyle,Reese[15]提出的剪应力传递双曲线模型求得。若已知桩的挠曲变形y,桩侧剪应力可由式(10),式(11)确定:

τi=(SLτ)i(τult)i

(10)

(τult)i=ζα(su)i

(11)

其中,α为黏滞系数,正常固结土取值为1,超固结土可取值0.5;ζ为深度修正系数,为方便计算,将双曲线模型按深度分为三部分:深度3 m以内,取ζ=0.53,深度3 m～6 m时,ζ取0.85,深度超过6 m时,ζ=1。

3 应变楔理论计算流程及实例

3.1 应变楔理论计算流程

在建立应变楔理论计算模型时,将抗滑桩视作岩土体内一竖向放置的弹性地基梁并建立挠曲线方程[16-17],将桩嵌固端深度划分为若干层,假定土体当前的侧向应变ε和被动楔形体的深度h(即零挠度点的深度)[18];利用差分法,通过迭代求解嵌固端桩身以下所有节点的位移yi,再计算桩身任意节点的转角、弯矩、剪力和土体抗力,具体流程如下:

1)计算每层土体中心的有效自重应力σv0,根据模型和公式分别确定砂土或黏土的极限应力Δσhf。然后基于土的双曲线应力应变关系式确定被动楔形体中的水平应力Δσh。

2)根据假定深度h评估土体被动楔的相关几何形状,当土体为砂土时算出应力水平SL即可通过式(4)得到扇角φm,黏土则需要进行有效应力分析算出孔隙水压力Δu后再计算φm。根据伞角φm及应变楔模型的几何关系,可以计算出底角θm和楔面的宽度。

3)分别按公式计算砂土或黏土中桩侧垂直剪应力τv,并求解得到抵抗弯矩MR;根据地基反力系数Es的当前曲线和抵抗弯矩MR,在任意桩头水平荷载Q下,将水平受荷桩作为BEF进行有限差分法分析。将使用BEF分析评估的桩头挠度y0和零挠度点深度h值与应变楔模型分析假设的值进行比较。

4)对于相同的土体应变ε值,通过几个迭代过程,获得了h和y0的收敛值,对于下一步加载,使用较大的水平土体应变值ε,并重复上述步骤。当计算误差[y-y0]<10-5时,输出计算结果,获得某一荷载下嵌固段桩身的水平位移y。

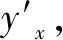
(12)

其中,h1为滑动面以上的桩身长度。

3.2 砂性土应变楔计算实例

以朱斌等[19]在砂土中的单桩试验模型为实例。本次选取S-2号桩进行计算,S-2号试验原型桩直径2.5 m,钢板壁厚0.045 m,加载高度为6.75 m,埋深45 m,EI(抗弯刚度)=55.67×106kN·m2。试验桩所处砂土有效重度9.46 kN/m3,平均粒径d50=0.000 16 m,相对比重为2.623,最大内摩擦角37.7°,泊松比为0.21,最大孔隙比0.952,最小孔隙比0.607,相对密实度介于60%～65%。计算结果如图4所示。

从图3中可以看出,在砂土中采用应变楔模型分析方法计算得到的桩身位移均大于实测值,因此可以认为应变楔模型分析方法在计算结果上较为安全。

3.3 不同桩径条件下m法与应变楔法计算结果比较

以上面实例分析土质及受荷条件下,分别采用m法与应变楔理论法,计算桩径1 m,1.5 m,2.0 m,2.5 m时桩的水平位移,计算结果如图5所示。

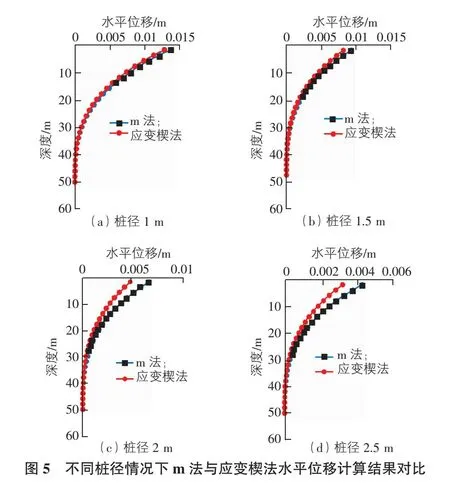
从图5中可以看出,桩径小于2 m时,两者计算结果相差不大,应变楔法较m法的桩顶水平位移计算结果偏小5.64%;但当桩径超过2 m后,两者计算的桩顶位移结果相差明显增加,m法计算的结果较应变楔法的计算结果增加45%以上。这可能是因为m法无法考虑大直径桩后及桩侧的土体作用[20]。因此,在小直径水平受荷桩位移计算时,m法与应变楔均适用,两者计算结果相差不大,且计算结果均大于实测值,偏向保守,而应变楔法更接近实测值。当桩径直径超过2 m时,m法计算结果误差较大,建议采用应变楔法。

4 结论

传统应变楔模型因需要进行复杂的应力水平进行计算而难以推广,本文引入前人提出的双曲线本构模型修正传统应变楔应力应变关系,简化了应变楔理论计算方法。应变楔模型所需的土体常用参数有条件的可以通过试验确定,否则可以根据经验公式。大直径单桩横向位移要求较高,桩侧垂直剪应力的影响不容忽视,本文分别采用m法和应变楔法,对不同直径下的水平受荷桩的横向水平进行计算,计算结果表明,当直径超过2 m时,采用应变楔法计算桩顶水平位移更符合实际情况。