基于SRCKF 算法的多自由度非线性系统动载荷识别方法

龚璟淳，陈清华，厉砚磊，王开云

（西南交通大学轨道交通运载系统全国重点实验室,四川 成都 610031）

准确快速地识别机械系统的动载荷对系统的振动响应测量、结构参数优化、疲劳寿命预测等具有重要意义。对于轨道车辆、飞行器等复杂非线性系统，直接测量轮轨作用力、飞行器外载荷等十分困难。因此，研究识别精度高、响应速度快的动载荷的间接识别方法具有重要的工程实用性。

动载荷识别方法主要分为时域识别法和频域识别法。频域识别法经过多年发展已较为成熟，其识别精度高但对噪声敏感，只适用于稳态动载荷和平稳随机载荷[1]。时域识别法起步较晚，其基本原理是将系统运动方程进行模态坐标变换，将动力方程解耦，再根据卷积后的激励与系统响应的关系识别出动载荷。武江凯等[2]以二次多项式为基函数，基于Duhamel 积分推导建立了一种针对单自由度振动系统的动态载荷识别方法。樊懿葳等[3]在此基础上通过模态坐标变换法，将多自由度振动系统运动方程解耦，建立了一种以系统加速度为输入的多自由度振动系统动载荷时域识别方法。以上研究均针对线性系统，难以解决非线性系统的载荷识别问题。

卡尔曼滤波是一种结合模型先验估计和测量更新的状态估计算法[4-6]。马也驰等[7]基于卡尔曼滤波方法和最小方差估计方法，分别建立了以系统位移和加速度为输入参数的激振力时域识别方法。Impraimakis 等[8]设计了一个新型无迹卡尔曼滤波器，实现了非线性系统所有动态状态参数和输入参数的实时联合识别。LIU 等[9]基于扩展卡尔曼滤波方法，引入主成分分析（PCA）方法变换多维区间模型，建立了一种用于线性系统动载荷识别的动态力重构方法。许多研究[10-12]表明，卡尔曼滤波在载荷识别方面具有很强的实用性。

平方根容积卡尔曼滤波（SRCKF）[13]是一种基于三阶球面径向容积准则和平方根滤波的改进卡尔曼滤波算法。穆静等[14]应用SRCKF 算法对未知弹道系数的再入弹道目标实现了快速精确的状态估计。肖仁鑫等[15]基于SRCKF 算法结合遗忘因子，对电池荷电状态进行在线辨识。以上研究表明，在非线性过程问题中，平方根容积卡尔曼滤波算法有较好的估计效果。

针对铁道车辆车钩等存在非线性刚度阻尼的单一维度、多自由度系统的外部动载荷，本文提出了一种基于SRCKF 算法的多自由度非线性系统动载荷识别方法，通过建立包含动载荷的系统状态非线性递推函数，结合平方根容积卡尔曼滤波算法和系统各部件振动加速度响应来更新估计动载荷。为验证算法可行性，本文以二自由度非线性弹簧阻尼振子系统为例分析了该算法对随机激励和组合谐波激励的识别效果。

1 非线性系统建模与识别算法

1.1 二自由度非线性弹簧阻尼模型

以具有刚度非线性和阻尼非线性的弹簧振子串联振动系统为研究对象，如图1 所示，系统的振动方程为

式中：M为系统质量矩阵；C为系统阻尼矩阵；K为系统刚度矩阵；X、和分别为系统的位移、速度和加速度向量；F为系统动载荷。

在刚度非线性系统中，k1具有非线性特性，如图2 所示，弹簧力计算公式为

图2 非线性刚度特性示意图Fig.2 Diagram of nonlinear stiffness characteristics

式中：k1i（i=1～3）为刚度系数；b为相对位移；δi（i=1～2）为间断点对应位移值；sign()表示对取变量的正负号。

在阻尼非线性系统中，c1具有非线性特性，如图3 所示，阻尼力计算公式为

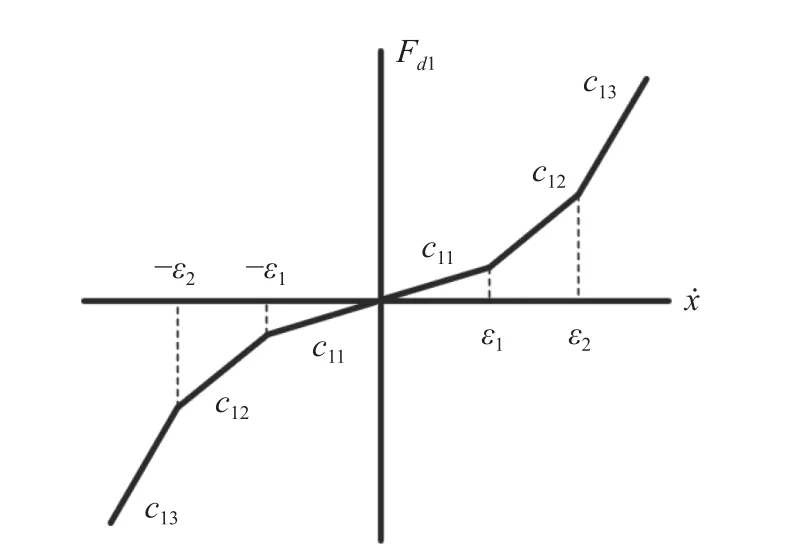
图3 非线性阻尼特性示意图Fig.3 Diagram of nonlinear damping characteristics

式中：c1i（i=1～3）为阻尼系数；为相对速度；εi（i=1～2）为间断点对应速度值。

1.2 SRCKF 算法识别原理

对于上述二自由度系统模型，其状态变量为

式中：z1、z2分别为质量块m1、m2的垂向位移；、分别为质量块m1、m2的垂向速度。

将振动系统所受动载荷看作系统内在状态，将状态变量扩充为

此时振动系统的状态空间方程为：

对于系统的位移、速度和加速度响应，在实际工程应用中，加速度响应相比位移和速度响应更易测量，因此，选择系统中各部件振动加速度作为系统观测量，为

实际上传感器测量的数据为离散采样，因此，将系统状态方程离散化。根据固定积分步长采用四阶龙格库塔法对递推式进行时域积分迭代更新。

式中：xk∈Rnx为系统状态变量；zk为观测量。过程噪声wk-1和量测噪声vk为相互独立的高斯分布，即wk-1～N(0,Qk-1)，vk-1～N(0,Rk-1)。

结合以上公式，采用平方根容积卡尔曼滤波算法对系统动载荷的识别流程如图4 所示。核心步骤是根据识别的第k-1 步的状态变量xk-1递推出第k步的状态变量xk识别值。首先对状态变量x0和误差协方差矩阵P0进行初始化，给定过程噪声矩阵Q和测量噪声矩阵R的初始值。然后进行时间更新，通过xk-1计算容积点Xj,k-1，将容积点代入非线性状态方程计算传播后的容积点，再计算k时刻状态量预测值和误差协方差矩阵的平方根，为：

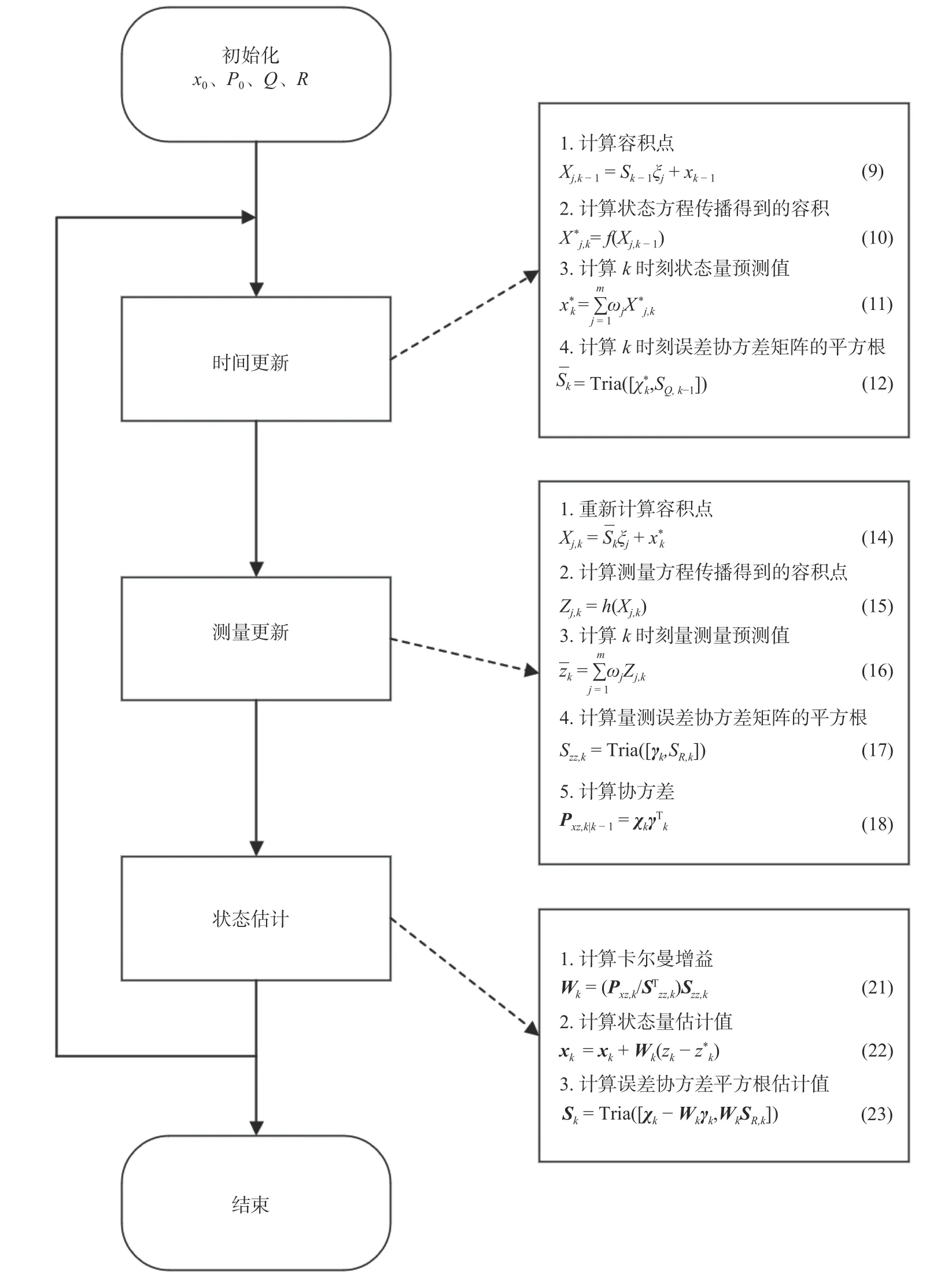
图4 SRCKF 算法流程图Fig.4 Algorithm flow chart of SRCKF

式中：Sk-1为Pk乔列斯基分解后得到的上三角矩阵；ξj（j=1～m）为容积点集；Tria()表示对矩阵进行三角化，获得矩阵的方阵；为中心加权矩阵，为

接着进行测量更新，根据k时刻状态量预测值和误差协方差矩阵的平方根计算容积点Xj,k，将Xj,k代入测量方程进行传播，得到传播后的容积点Zj,k，再计算k时刻的测量量预测值、测量误差协方差矩阵的平方根和误差协方差矩阵Pk，为：

式中SR,k为Rk的平方根。γk、χk定义为：

最后，计算卡尔曼增益Wk、状态量估计值xk和误差协方差矩阵平方根估计值Sk，完成一次状态更新。

通过连续的状态更新过程，就能实现振动系统动载荷的实时识别。

2 算法验证

以图1 所示的二自由度非线性振动系统为例进行验证。系统的各部件质量为m1=4 kg，m2=8 kg，刚度非线性系统参数如表1 所示，阻尼非线性系统参数如表2 所示。

表1 刚度非线性系统参数Tab.1 Stiffness parameters of nonlinear system

表2 阻尼非线性系统参数Tab.2 Damping parameters of nonlinear system

采用相关系数和均方根误差值对识别结果进行判断。相关系数能描述识别结果的变化趋势，均方根误差值侧重于衡量真实值与识别值之间的差异。均方根误差计算公式为

式中：y为真实值；为预测值；m为观测次数。

2.1 随机激励识别

图5 为随机激励作用下刚度非线性系统动载荷识别的时域图、频域图和均方根误差图。可以看出，系统动载荷的识别曲线和仿真输入曲线十分接近，识别曲线和动载荷曲线的相关系数达0.997。由图5（b）可知，在动载荷高于0.8 Hz 频段时识别结果十分准确，低于0.8 Hz 频段识别结果存在较小误差。由图5（c）可知，在识别过程开始时，均方根误差达到最大值17.553 N，随后快速减小并稳定在2.052 N 以下。

图5 刚度非线性系统随机激励识别结果图Fig.5 Results of random excitation identification for nonlinear stiffness systems

图6 为随机激励作用下阻尼非线性系统动载荷识别的时域图、频域图和均方根误差图。从图6（a）可以看出，识别曲线和真实曲线大致重合，相关系数达0.999。图6（b）的频域结果表明，在各个频段识别效果都很好。图6（c）显示均方根误差在识别过程开始时出现最大值1.258 N，随后急剧减小并稳定在0.033 N 以下。

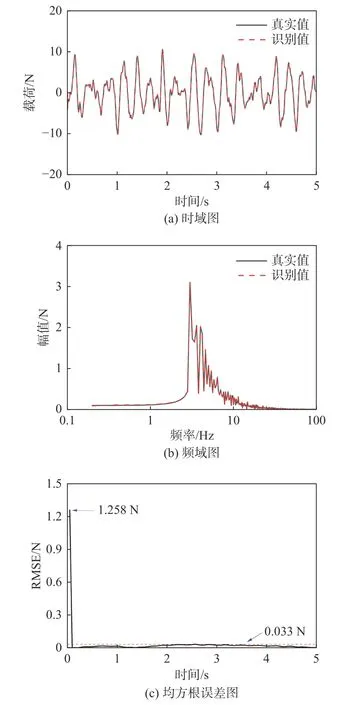
图6 阻尼非线性系统随机激励识别结果图Fig.6 Results of random excitation identification for nonlinear damping systems

2.2 组合谐波激励载荷识别

图7 为对刚度非线性系统施加频率为1、2、3、5 和7 Hz 的组合谐波激励时的动载荷识别结果。图7（a）的动载荷时域识别图表明，识别曲线和动载荷曲线变化趋势一致，相关系数为0.997。图7（b）的频域动载荷曲线和识别曲线的对比可知，在频率大于0.8 Hz 时识别效果较好，在小于0.8 Hz 时，随着频率的减小，识别误差逐渐增大。由图7（c）的系统动载荷曲线和识别曲线的均方根误差可知，识别过程中均方根误差存在一定波动，最大值为0.866 N，均方根误差整体处于较低的水平。

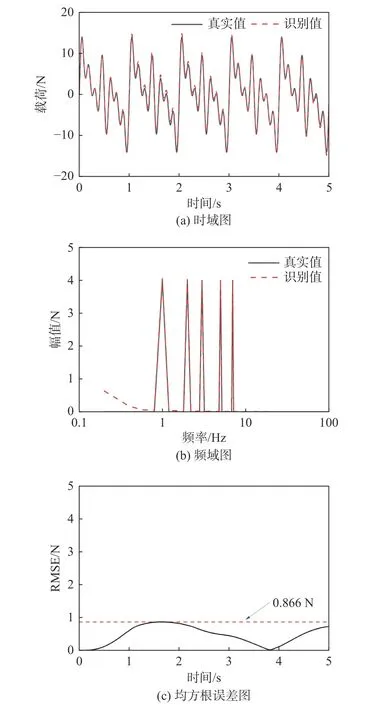
图7 刚度非线性组合谐波激励识别结果图Fig.7 Results of harmonic excitation identification for nonlinear stiffness systems

图8 为对阻尼非线性系统施加频率为1、2、3、5 和7 Hz 的组合谐波激励时的动载荷识别结果。图8（a）表明，识别曲线和真实曲线基本重合，二者的相关系数达0.999。由图8（b）可以看出，在频率大于0.8 Hz 时识别曲线和动载荷曲线基本重合，在频率小于0.8 Hz 时识别幅值偏大。从图8（c）可以看出，识别值与真实值的均方根误差随识别过程不断变化，其最大值为0.234 N，整体收敛在一个较低的水平。

图8 阻尼非线性系统组合谐波激励识别结果图Fig.8 Results of harmonic excitation identification for nonlinear damping systems

3 结论

本文基于SRCKF 算法提出了一种多自由度非线性振动系统动载荷的识别方法，并通过二自由度的刚度非线性和阻尼非线性的弹簧阻尼振子系统对算法进行了验证。

1）在刚度非线性系统上施加随机激励和组合谐波激励时，识别曲线与输入载荷曲线相关系数均达0.997。在阻尼非线性系统上施加随机激励和组合谐波激励时，识别曲线与输入载荷曲线相关系数均达0.999。

2）在频率大于0.8 Hz 的频段，识别结果与输入载荷基本吻合。在小于0.8 Hz 的低频段，识别结果存在一定误差。

3）对于随机激励，识别结果的均方根误差的最大值出现在识别初始时，随着识别过程的进行，识别的误差逐步收敛至较低的水平；对于组合谐波激励，识别结果的均方根误差存在小幅波动，整体处于较低水平。