面向低空无人机运行的高精度卫星测速算法

吉 莉，孙 蕊*

（1.南京航空航天大学海上智能网信技术教育部重点实验室,江苏 南京 211106；2.南京航空航天大学空中交通管理系统全国重点实验室,江苏 南京 211106）

我国北斗卫星导航系统（Beidou satellite navigation system,BDS）的建成带动了全球导航卫星系统（global navigation satellite system,GNSS）的快速发展。星基导航技术逐渐发展并应用于无人机低空运行的各个方面。准确可靠的速度信息对无人机自主感知和状态控制发挥着十分重要的作用，然而由于无人机体积与重量的限制，搭载额外的传感器必然会增加成本，而低成本的GNSS 测速则十分切合无人机的自主状态感知需求。GNSS 测速方法主要有多普勒法、历元间载波相位差分法（time-differenced carrier phase,TDCP）以及历元间伪距差分法（time-differenced pseudorange,TDPR）[1 -2]。由于载波相位精度较高，TDCP 方法自提出以来就得到了广泛研究，但在观测质量较差的环境下，载波相位观测值容易受到污染，从而严重影响测速精度。通过将TDCP 观测值与其他传感器融合可以提供稳健的速度信息，例如：Han 等[3]将GNSS 与惯性导航系统（inertial navigation system,INS）组合以固定模糊度；Kim 等[4]将GNSS/INS 组合进行周跳检测和修复。但以上方法需要额外的惯性器件，增加了成本以及计算负担。此外，Li 等[5]提出了基于卡尔曼滤波平滑的测速算法，但算法存在过于依赖运动模型、在高动态环境下可靠性不足的问题。

针对上述问题，考虑城市低空无人机运行环境的实际特征，本文充分应用TDCP 观测信息，提出了一种面向低空无人机运行的高精度卫星测速算法。该算法首先通过多普勒辅助的TDCP 方法得到无人机运行的航向角，然后通过卫星方位角与无人机的航向角夹角构建加权模型并解算测速结果，最后采用抗差卡尔曼滤波以减小粗差的影响，从而提高了测速结果的鲁棒性。

1 研究与方法

1.1 算法框架

基于卫星方位角加权的多普勒辅助TDCP 测速算法如图1 所示。

图1 算法框架Fig.1 Algorithm framework

步骤1，根据GNSS 接收机接收到的观测文件和星历文件获取载波相位、多普勒频移观测值以及卫星位置，进一步得到卫星位置变化量以及接收机与卫星的方向向量，从而根据历元间载波相位差分方程解算历元间接收机位移 ∆rR。

步骤2，根据接收机的历元间位移由几何关系估计无人机航向角θ，得到每颗卫星的方位角 Az与无人机航向角 θ 的夹角µ。基于卫星仰角、载噪比以及方位夹角构造权矩阵W。

步骤3，根据历元间载波相位差分方程基于加权最小二乘法求解无人机速度V。

步骤4，基于抗差卡尔曼滤波对步骤3 解算的无人机速度进行滤波平滑，得到最终测速结果。

1.2 多普勒辅助的TDCP 解算位置增量

载波相位观测模型可以表示为

式中：φ为以周数表示的载波相位观测值；λ为载波的波长，r为卫星与接收机之间的几何距离；c为光速；I和T分别为电离层延迟和对流层延迟；dtR和dtS分别为接收机钟差和卫星钟差；N为载波的整周模糊度；ε表示观测噪声和其他未建模误差。在较短的采样间隔内，上述误差近似不变，同时整周模糊度在载波跟踪环路保持锁定时也可保持不变，因此，通过对载波相位观测方程在历元间做差分可得

式中：∆φ和 ∆r分别表示载波相位和卫星与接收机间的几何距离在相邻历元间的变化量；∆dtR表示接收机钟差漂移。考虑到卫星与接收机之间的几何距离远大于历元间接收机的位置变化量，因此，前后历元由卫星指向接收机的单位向量可近似相等，根据几何关系可得

式中：uk为卫星指向接收机的单位向量，和分别为历元k和k-1卫星的位置；分别表示对应历元接收机的位置；∆rS和 ∆rR则分别表示卫星和接收机在历元间的几何位置增量。将式（3）代入式（2）并改写成向量模式可得

在开阔环境及静止环境中，载波相位观测值具有更高的精度，但当接收机处于更为复杂的环境中或高动态状态时，多普勒观测值具有更高的可靠性和稳健性；因此，用多普勒观测值辅助TDCP 以充分发挥2 种观测值的优势。载波相位差可以由多普勒频移的一阶中心差分来近似[6]，即

式中：Dk和Dk-1分别表示历元k和k-1的多普勒频移；∆t为采样间隔。将式（5）代入式（4）可得

当卫星数满足定位条件时，可根据式（6）解算接收机在地心地固坐标系（earth-centered earthfixed,ECEF）中的历元间位移∆rR。

1.3 基于位置增量的航向角估计

当接收机采样率较高时，可认为其位移方向与无人机航向近似相同。接收机在东北天（eastnorth-up,ENU）坐标系下的历元间位移可由ECEF 坐标系中的∆rR旋转得到，为

由几何关系得到无人机的航向角[7]，为

1.4 加权最小二乘模型构造

卫星的观测值质量通常与电离层延迟、对流层延迟以及多径误差有关。多普勒辅助的TDCP模型由于对历元间的电离层和对流层延迟进行了近似处理，其误差主要体现在多路径误差上。高度角较小的卫星信号往往更易受到建筑物的反射，会造成更大的多路径误差干扰；载噪比也反映了观测值的质量，载噪比较高的卫星通常观测质量更好：因此，在解算时可以构造一个权矩阵，降低高度角和载噪比较低的卫星的权重[8]。目前最为广泛使用的是基于高度角和载噪比的加权模型[9-14]。卫星的测量误差标准差 σ可表示为

式中：a0、a1为经验系数，通常a0=0.3、a1=2.6；El0为卫星的参考高度角，通常取为20°，El为卫星的实际高度角；S为缩放因子，由卫星信号的载噪比C/N0决定，即

无人机在城市低空环境飞行时，其运动方向大致为城市道路沿街方向，当卫星处于沿街方向范围时，可认为其信号受到遮挡的可能性较小，当处于过街方向时则认为其信号更容易受到建筑物的遮挡和反射。因此，应对沿街方向的卫星赋予更高的权值，而对过街方向的卫星降低权值。

记卫星方位角与无人机航向角所在直线的夹角为µ，µ∈[0,π/2]，则µ 可表示为

式中 Az 为卫星的方位角，A z ∈[0,2π)。

在式（9）的基础上，进一步加入由夹角 µ决定的缩放因子m，构造考虑卫星方位角的加权模型为

缩放因子m由指数函数模型自定义，为

式中 µ0为参考夹角，取值为90°。

卫星权重取值为测量误差标准差的倒数，为

当观测到颗卫星时，可以构造权矩阵为W=diag(w1,w2,···,wj)。对所有的卫星联立式（6）可得矩阵形式，为

则加权最小二乘解为

最终得出基于卫星方位角加权的无人机速度，为

1.5 抗差卡尔曼滤波

在观测环境较差或出现异常观测值时，速度观测值可能会出现较大偏差。由于无人机的速度存在变化的连续性，因此，本文使用抗差卡尔曼滤波对无人机速度进一步估计以得到更加稳健的速度估计值。输入卡尔曼滤波器的状态向量为

式中Vx、Vy、Vz分别表示滤波估计的无人机三维速度分量。

以匀速运动模型构建的抗差卡尔曼滤波的递推公式为：

式中：χk,k-1表示由 χk-1递推的一步预测状态向量；Pk,k-1为一步预测的状态协方差矩阵；Qk-1为运动模型的误差方差矩阵；Zk为观测向量，即上一步所得的无人机速度；Resk为新息；Kk为增益矩阵；Rk为观测噪声矩阵；χk为历元k的状态估计向量；Pk为χk的状态协方差矩阵；ωk为抗差因子矩阵。对 ωk中的每一个元素，均有

2 结果与分析

为验证所提测速算法的性能，在南京市区道路进行了2 组实验，分别为南北向和东西向飞行场景，参考轨迹分别如图2 及图3 所示。本次实验采用浙江中裕通信的ZYACF-S806 天线与北斗星通的C520-AT 接收机搭配进行GNSS 观测，使用采集到的BDS 数据进行实验验证。实验1 的数据采集时长为243 s，采样频率为10 Hz，共计2 430 个历元；实验2 采集时长为550 s，采样频率为10 Hz，共计5 500 个历元。由霍尼韦尔的高精度组合导航系统HGuide N580 采集参考数据，并由商业软件Inertial Explorer 进行后处理解算获取速度参考值。

图2 实验1 参考轨迹Fig.2 Reference rack of onboard experiment 1

图3 实验2 参考轨迹Fig.3 Reference rack of onboard experiment 2

2 组实验期间的可见卫星数量分别如图4 及图5 所示，表明实验数据采集场景下的可见BDS卫星数满足测速解算的条件。根据采集的BDS 观测数据分别基于传统TDCP 算法和本文算法进行速度解算。

图4 实验1 可见卫星数Fig.4 Number of visible satellites in experiment 1

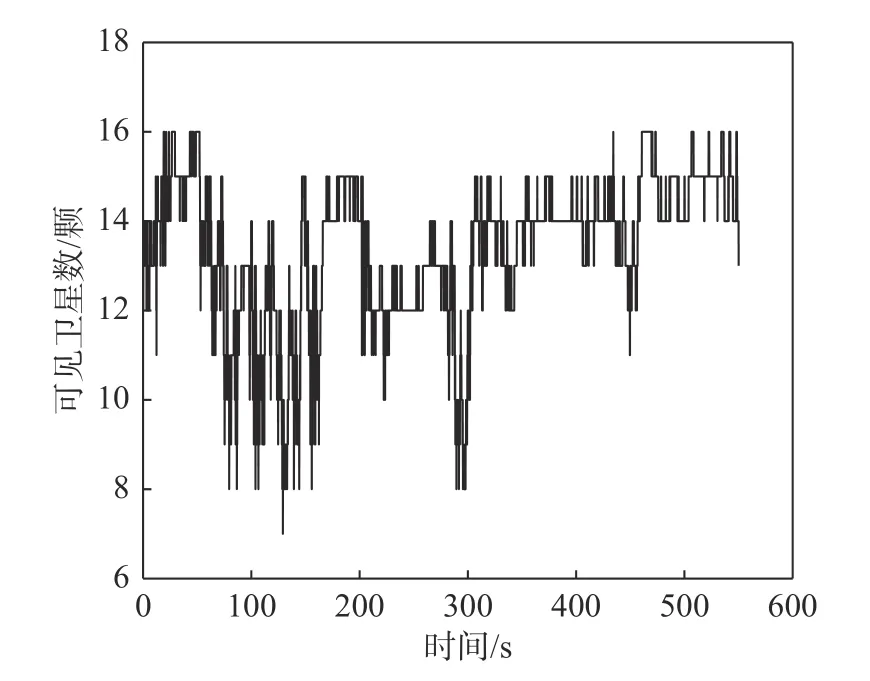
图5 实验2 可见卫星数Fig.5 Number of visible satellites in experiment 2

实验1 在三维方向上的测速误差如图6 所示，图中对比了传统TDCP 算法和本文算法的测速性能。可知，本文算法的测速精度比传统TDCP 算法更高，大部分误差峰值得到了抑制。本文通过测速均方根误差（root mean square error,RMSE）来表征测速精度。由表1 的传统TDCP 算法和本文算法的RMSE 值可知，本文算法的三维RMSE 分别为0.048 0、0.109 3 和0.2170 m/s，相对于传统TDCP算法，其在东向、北向和天向上分别实现了32.23%、10.37%、50.39%的提升。其中，东向的提升率高于北向，这是因为实验1 的轨迹为由南向北，基于卫星方位角的加权算法抑制了垂直于轨迹方向上的误差，因此，东西方向能够实现更好的测速精度提升。

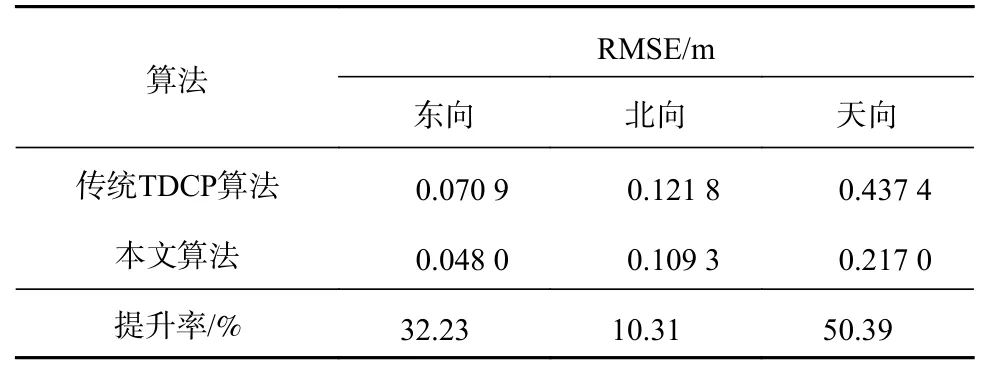
表1 实验1 算法误差均方根对比Tab.1 RMSE comparison of the algorithms

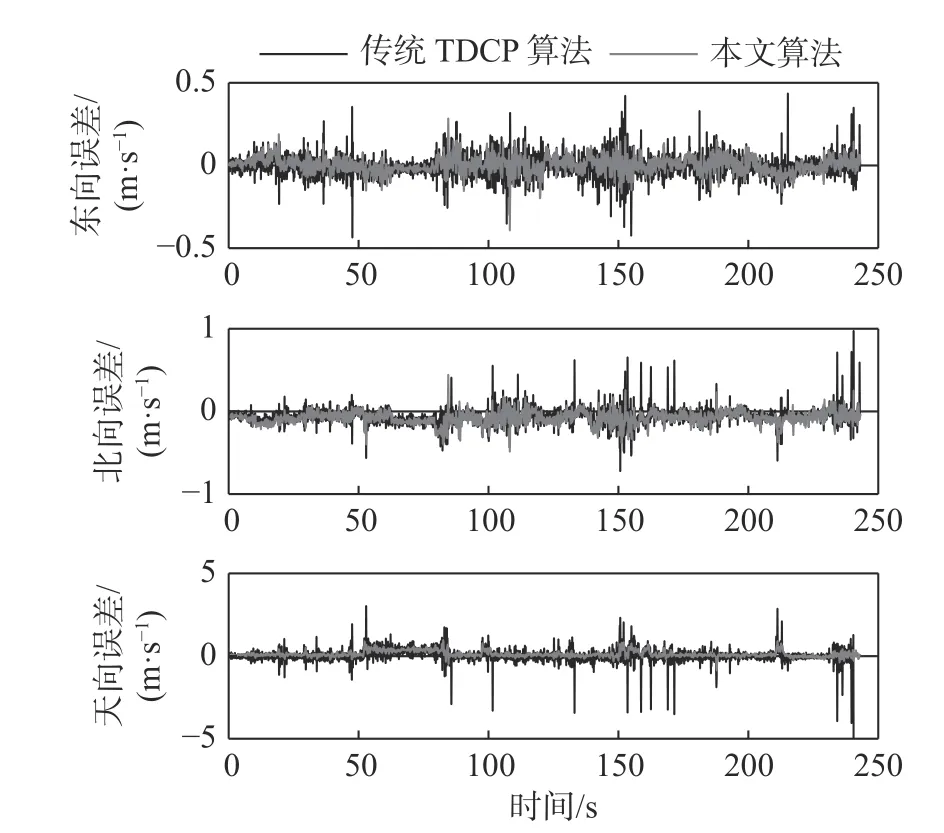
图6 实验1 算法误差对比Fig.6 Errors comparison of the algorithms in experiment 1

实验2 在三维方向上的RMSE 如图7 所示，算法的RMSE 以及提升率如表2 所示。实验2 的结果同样证明了本文算法可以实现测速精度的有效提升。其中，本文算法相对于传统TDCP 算法在东向、北向、天向上的测速精度分别提升了10.20%、30.19%和31.54%。由于实验2 的轨迹为东西方向，因此，本次实验在南北方向实现了更好的测速精度提升。

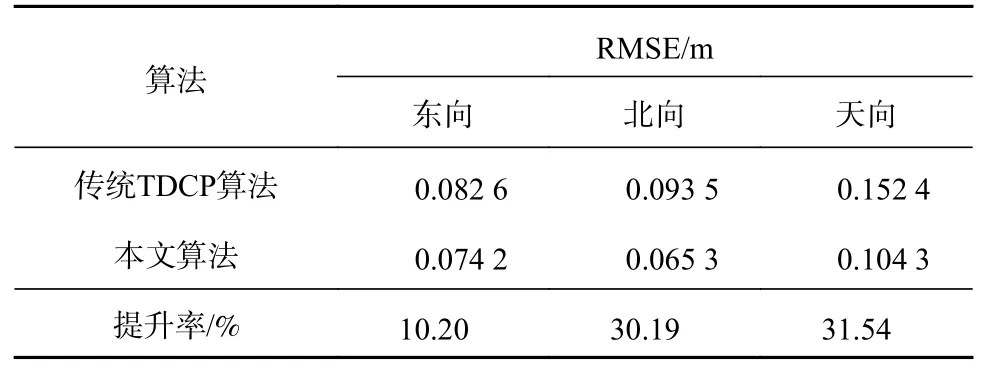
表2 实验2 算法误差均方根对比Tab.2 RMSE comparison of the algorithms in experiment 2

图7 实验2 算法误差对比Fig.7 Errors comparison of the algorithms in experiment 2

结合2 组实验结果可知，本文基于卫星方位角加权的多普勒辅助TDCP 测速算法相对于传统TDCP 算法能够在城市低空无人机运行环境中实现更高精度的无人机测速。

3 结论

1）针对传统TDCP 测速算法在城市低空无人机运行环境中存在测速精度不足的问题，利用TDCP 解算的无人机航向角信息，构建了一种面向低空无人机运行的高精度卫星测速算法，融合多普勒与载波相位观测值，并将基于卫星方位角的加权和抗差卡尔曼滤波应用于测速解算中，改进了传统TDCP 测速算法，从而提升了算法的精度和鲁棒性。

2）实测实验结果表明，相较于传统TDCP 测速算法，本文的基于卫星方位角加权的多普勒辅助TDCP 测速算法在不同实验场景下三维方向的测速误差分别降低了32.23%、10.37%、50.39%和10.20%、30.19%和31.54%，说明本文算法可以实现测速精度的明显提升。

3）本文算法原理简单且成本低廉，仅需通过GNSS 接收机已有的数据即可实现速度信息的获取，对于城市低空无人机的自主感知具有较高的应用价值。本文算法也可应用于车载导航等其他领域。