基于三维反演重构的微波着陆系统飞行校验评估方法

罗 潇，史晓锋

（北京航空航天大学电子信息工程学院,北京 100191）

飞行校验是保障航空运输安全必不可少的技术手段，其旨在检查和评估各种导航、雷达、通信等设备的空间信号质量及其容限。微波着陆系统（microwave landing system,MLS）作为一种新型着陆引导系统，目前主要用于军用航空领域，可在一广阔的覆盖区内提供位置信息，并以方位角、仰角和距离进行度量。相较于目前机场广泛使用的仪表着陆系统（instrument landing system,ILS），其适应性强、覆盖范围广、制导精度高。面对日益复杂的空中交通情况，MLS 在民用航空领域具有广阔的发展前景。在着陆引导系统飞行校验的研究领域，李小强等[1]提出了一种基于双VDB 台站的卫星导航地面增强系统飞行校验方法，陆永东等[2]对仪表着陆系统飞行校验方法进行深入的对比研究，Yang 等[3]提出一种基于模糊集决策的ILS 飞行校验中的参数异常检测方法，但针对MLS 飞行校验和测试评估方法在国内民用航空领域尚未完善。本文依据国际标准对MLS 的飞行校验进行研究，分析了校验关键参数及其容限要求、校验基准的选取以及飞行科目设计，同时针对MLS 飞行校验过程中可能出现空间信号漏检等问题，提出一种基于有限稀疏样本条件下利用径向基函数神经网络对MLS 场型进行三维反演重构的方法，实现了MLS 完整空间信号场型评估。

1 MLS 飞行校验

1.1 关键参数与容限要求

MLS 作为用于引导飞机着陆的系统，对其进行飞行校验，关键在于评估MLS 系统引导着陆的精度是否符合要求。对MLS 的系统误差进行分析，其输出信号的角频率分为航道跟随误差（path following error，PFE)和控制运动噪声（control motion noise，CMN）。航道跟随误差包含航道跟随噪声和平均航向道误差或平均下滑道误差，是由系统或设备提供的角度和距离数据误差中的慢变化（频率较低）成分，这种成分的误差属于可能引起飞机偏离预定航向道和/或下滑道的引导信号误差分量，其指预定飞行航迹和实际飞行航迹(按引导信号飞行时)之间的偏差。控制运动噪声则是指由系统或设备所提供的角度和距离数据误差中的快变化成分（频率较高），这种成分的误差会导致飞机舵面和操纵杆的抖动，当CMN 过大时，说明飞机飞行不平稳。

为获得PFE 和CMN，需要对误差分量进行解构剥离。根据飞机着陆过程的动态响应特征，通过转折频率为10 弧度/秒的低通滤波器可以获得PFE 和CMN 分量。其中PFE 包括小于或等于0.5 弧度/秒的方位误差成分和小于或等于1.5 弧度/秒的仰角误差成分；CMN 则包括那些处于0.3～10 弧度/秒范围内的方位误差成分和处于0.5～10 弧度/秒范围的仰角误差成分[4]。具体测量滤波器配置如图1 所示。

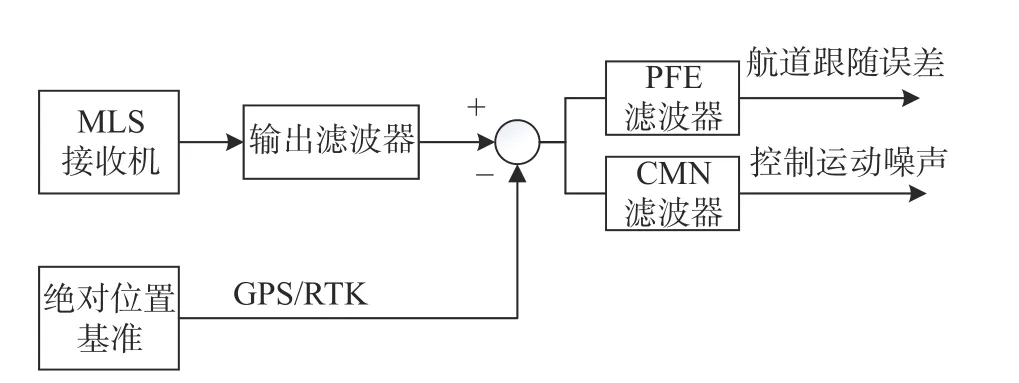
图1 滤波器配置Fig.1 Filter configuration

PFE 和CMN 可以直接反映飞机着陆过程中的制导误差和舵面响应，因此评估这两个参数在空间内的分布是否符合容限要求是MLS 飞行校验的关键。为获得PFE 和CMN 在空间的容限分布，本文基于ICAO 8 071 附件十[5]以及FAA8200 飞行校验规范手册[6]，分析MLS 覆盖区内的误差评估方法。其中在MLS 系统引导着陆的过程中，系统在跑道入口处的精度决定了着陆质量，因此跑道入口处是精度的主要测量点。以方位制导为例，MLS 信号的覆盖范围如图2 所示。在跑道入口和跑道中线的交叉点上方定义了一个“MLS 基准点”。当飞机进入MLS 覆盖范围时，都以此点作为基准，覆盖范围内的其余地方精度要求随着距离或偏移角度增大而降低，即PFE 和CMN 的容限将随着离基准点的距离、横向偏移角度和仰角而变化。同时，按照规范要求，其变化规律与距离或偏移角度呈线性关系。

图2 MLS 方位制导覆盖图Fig.2 MLS azimuth coverage

本文结合PFE 和CMN 在基准点处的容限要求以及跑道路口以外的降级容限要求，推算PFE 和CMN 在整个覆盖空间内的容限分布。进近基准点处的容限要求如表1 所示（距离形式）。

表1 进近基准点处容限要求Tab.1 Tolerance requirements at approach reference points

具体步骤如下。首先将基准点处的容限值根据方位天线到基准数据点的距离转为极坐标形式

式中：θ为基准点处PFE/CMN 以角度形式的容限值，（°）；Tf为PFE/CMN 以距离形式的容限值，m；D为从方位天线到基准数据点的距离，m；k为米和英尺的转换系数。

在极坐标形式下，根据MLS 在跑道路口以外的衰减系数，可以得到覆盖范围内任意测量点处PFE/CMN容限值的分布函数为

式中：θ0为测量点处的容限值，（°）；r为测量点距离基准点的距离，海里；θp为横向偏移角度，（°）；θt为仰角，（°）；θm为规定的最低下滑道角度，（°）。

1.2 校验基准选取

校验基准的选取直接关系到飞行校验的可靠性及稳定性。飞行校验过程中飞机需要按照飞行科目采集规定路径上的信号数据。由于外界干扰，校验飞机在飞行过程中很容易发生航迹偏移，导致出现飞行误差，从而影响飞行校验的结果。为确保在不同位置获得准确的空间信息，需要选取合适的校验基准以建立空间信号采样的基准刻度。

根据ICAO 8 071 的飞行校验理论，校验精度（即校验基准精度）应至少为被校设备系统精度的3 倍[7]。考虑MLS 属于精密进近着陆引导系统，因此需要更高精度的空间定位技术作为校验的基准，如GPS/RTK 技术，其定位精度可达到厘米级，远远高于MLS 精度的3 倍以上。

1.3 飞行科目设计

选取合理的校验基准可以计算飞行校验中的关键参数，设计不同的飞行科目可以对不同航道上的关键校验参数进行采样。飞行科目的设计需要考虑整个测试区域的地形、地貌、气象等因素以及被校设备的工作范围，同时应尽量减少飞机在空域的暴露时间以保证飞行安全。MLS 不同于ILS 的单一航道进近，其支持曲线进近、分段进近等。MLS 飞行校验过程中，飞行科目包含的航道始终有限，只能获得有限的稀疏离散信号，难以对完整空间信号场型进行评估。因此，需要使获得的有限稀疏信号在空间中分布具有更强的空间相关性，进而推算出MLS 校验参数在整个覆盖区中的分布。设计合理的飞行科目以实现后续的场型反演重构尤为重要。

考虑MLS 信号覆盖范围（如图2 所示），其包含跑道中心线±40°，垂直面0～15°、距离基准点0～20 海里的扇形区域，因此飞行科目的设计在仰角上必须尽可能多地包含不同角度的下滑道，同时在方位制导上必须尽可能包括不同的横向偏移角度。本文结合FAA 8 200 中对MLS 的飞行校验规范，设计了一项包含多段航线的MLS 飞行科目，其飞行航迹如图3 所示，其中包括3°下滑角正直对准/斜对准航道、6°下滑角正直对准/斜对准航道、径向水平飞行以及多段不同距离的圆周飞行。

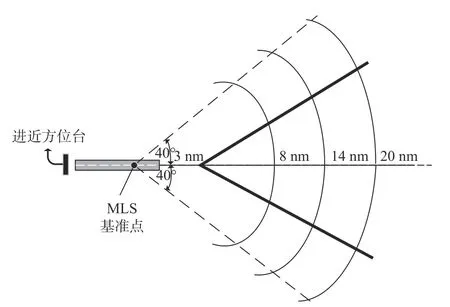
图3 飞行科目示意图Fig.3 Schematic diagram of flight subjects

2 三维空间信号场型反演重构

尽管设计的飞行科目包含多段航线，但相较于广阔的MLS 信号覆盖范围，校验过程中采集的数据仍然是稀疏信号，其本身就存在空间信号漏检的可能；因此，常规的飞行校验测试评估方法难以实现MLS 完整三维空间信号场型评估。在雷达信号、图像处理等领域，空间插值技术被广泛用于数据处理中，其可根据已知的稀疏样本数据点经过插值实现数据反演重构。基于MLS 的精度要求以及校验参数依赖于距离的分布特点，本文采用径向基函数神经网络插值法。利用采集的稀疏样本作为训练集，可在大范围内实现高精度的插值[8]，从而实现MLS 三维空间信号场型反演重构。

2.1 径向基函数（RBF）神经网络

径向基函数是一个取值仅仅依赖于离原点距离的实值函数,或者还可以是到任意一点c的距离,c点称为中心点,也就是 Φ(x)=Φ(‖x-c‖)[9]。常用的径向基函数包括以下函数。

Gaussian 函数：

Reflected sigmoid 函数：

式中：δ为函数的宽度参数，可以控制函数的径向作用范围。

径向基函数神经网络是一种使用径向基函数作为激活函数的人工神经网络。径向基函数网络的输出是输入的径向基函数和神经元参数的线性组合。其包含3 层神经网络结构，分别为输入层、隐藏层、输出层，只要隐藏层神经元足够多径向基函数神经网络（RBFNN）完全可以拟合任何一个函数。基于MLS 三维场型特点，定义RBFNN 的拓扑结构的输入层为3 个节点，分别对应曲面上点的坐标值Pi（x，y，z），输出层为一个节点对应曲面上的点Pi（x，y，z）对应的校验参数值。其网络拓扑模型如图4 所示。

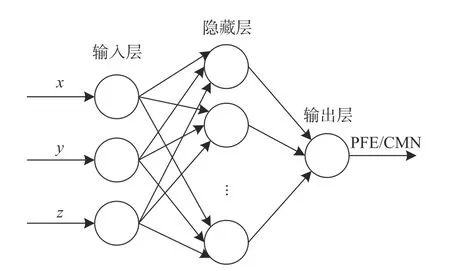
图4 网络拓扑模型Fig.4 Network topology model

利用径向基函数神经网络进行场型反演重构，即将空间中采集的稀疏数据点通过径向基函数映射到高维空间中，然后进行线性插值或拟合，得到空间内缺失数据点的估计值。其学习过程[10-11]如下。

记X=[x,y,z]为采集的稀疏样本数据点坐标，即为输入层的输入向量。设隐含层的节点个数为m,并记其径向基函数向量为H=[h1,h2,···,hm]T，其中hi为选择的径向基函数，表达式为

式中：X为输入向量；Ci为第i个隐含层神经元的中心向量；bi为神经元节点的基宽度。

记第i个神经元节点的中心向量为：Ci=[C1i,C2i,···,Cni]T，其中i=1,2,···,m。设构建网络基宽矢量为：B=[b1,b2,···,bm]T，其中bi为神经元节点的基宽度,且均为正常数。设构建网络的权值向量为：W=[w1,w2,···,wm]，则网络在t时刻的输出为

2.2 仿真验证

以方位制导的PFE 为样本，对径向基函数神经网络实现三维空间信号场型反演重构进行仿真实验，具体步骤如下。

1）模拟一组飞行校验过程中MLS 接收机采集的方位制导PFE 数据，实际飞行测试过程中MLS 方位制导数据刷新率约为13 Hz，飞机进近阶段速度大约230 m/s，而MLS 覆盖距离达到37 km，考虑干扰误差等因素，一条航线能获得大约1 000个有效空间采样点。

2）将模拟的PFE 数据作为训练样本，利用径向基函数神经网络，对覆盖区内未知航路点数据进行推算，实现三维空间信号场型反演重构。

3）分析重构后的场型误差。

设定机场情况为：方位台距离基准点7 965 英尺，机场规定的最低下滑角度为3°，在基准点处方位制导的PFE 容限值为20 英尺。图5 表示根据容限分布函数采样获得的PFE 样本分布情况。图6表示经过三维场型反演重构后PFE 在覆盖区域的分布。图7 表示反演重构的数据与样本数据之间的误差。

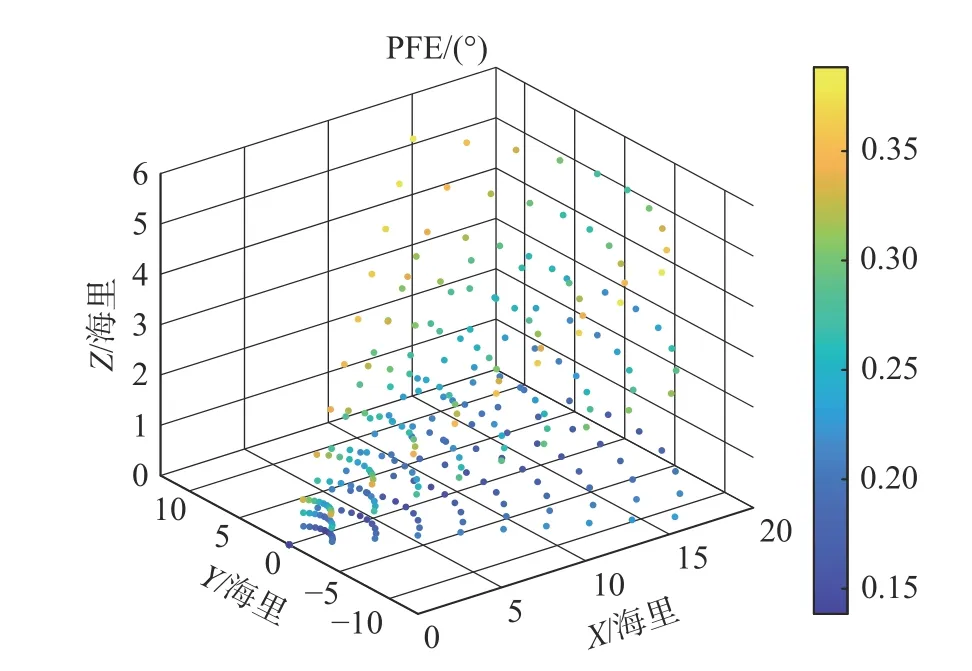
图5 PFE 样本分布图Fig.5 PFE sample distribution map

图6 PFE 反演重构后分布图Fig.6 PFE distribution map after inversion reconstruction

图7 反演重构的误差Fig.7 Error of inversion reconstruction

仿真实验结果表明，利用径向基函数神经网络实现的三维场型反演重构能够有效地描述PFE 在覆盖区的分布情况。基于1 000 个稀疏样本的训练，反演重构后的数据与模拟数据误差均在0.01°以内，根据设定的机场情况，其误差转化为距离形式大约为1.4 英尺（约0.4 m），远远小于表1 中FAA 8200 规定的20 英尺容限要求。同时实际飞行测试中，多段飞行航线采集的空间样本数量远大于1 000，反演重构的误差能进一步缩小。与传统的飞行校验测试评估方法相比，该方法仅需要少量稀疏样本信号就能对完整三维空间信号场型进行评估，大大提高了MLS 飞行校验的精度和效率。

3 结论

本文对MLS 飞行校验方法进行研究,得出以下结论。

1）针对尚未完善的规范要求，依据国际标准对校验中涉及的重点内容进行分析，为填补相关领域空白提供一定的借鉴。

2）针对飞行测试中采集的稀疏离散数据难以准确评估场型的问题，提出了一种利用径向基函数神经网络进行三维场型反演重构的方法。经过仿真验证，三维反演重构后航道跟随误差的重构误差大约为1.4 英尺，远小于FAA8200 飞行校验规范手册规定的20 英尺的容限要求，为MLS 飞行校验中完整三维空间信号场型评估方法提供了新的思路。