气动式撞击试验装置内弹道建模及性能影响因素分析

彭湃, 王军评, 毛勇建, 黄海莹, 李翀, 张军, 杨琪

(中国工程物理研究院总体工程研究所, 绵阳 621999)

特种装备或放射性运输容器等复杂涉危性物品在运输(公路、铁路、空运)和使用过程中,一旦遭受异常撞击等事故环境[1-3],结构将在强冲击载荷的作用下发生变形、破坏,并可能致使其内部的高能炸药或放射性物品在外界能量刺激下发生化爆或泄漏[4-7]。因此,异常撞击安全性问题已得到广泛的关注和重视,中外开展了大量的研究工作。

目前,撞击安全性的试验研究主要通过跌落塔、火箭撬、高空缆绳等[8-11]方式实现。跌落塔受自身结构形式的影响,其最大速度受限(速度一般小于40 m/s),一般用于模拟吊装、公路运输等较低碰撞速度的安全性研究。火箭撬的速度可以在每秒几十米至几千米的范围,高空缆绳通过自由跌落和火箭复合加速后最大速度可达244 m/s,承载能力可从数十克至数吨,但这两种试验设施占地面积大、造价昂贵、单次使用成本高,且在中低速段(几十至百余米每秒)加载速度离散性大[12](速度误差可能达到10%以上),可控性较差。

基于高压空气驱动的撞击试验装置为大负载试验件的撞击安全性研究提供了一种新的手段。该类型试验装置利用高压空气作为动力,可以在较短距离内推动吨级以上试件加速至每秒几十米到百米的发射速度,具有较好的经济性、可控性,弥补了跌落塔、火箭撬、高空缆绳等试验装置的不足[13]。对于该类型试验装置,发射速度的精确控制是试验成败的关键。特别是在试验实测数据有限的条件下,针对不同发射负载、不同发射速度需求的各种工况,如何实现发射速度的精准控制是亟待解决的问题。针对该问题,建立其工作过程的内弹道模型,是最直接有效的方法。

所述的撞击试验装置与传统的空气炮[14-15]试验装置相比,其结构组成、工作原理更复杂;与舰载机蒸汽弹射器[16-19]相比,有一定相似之处,但在高压气源的热力学特性、气缸密封特性、弹射动力学过程特性(牵制杆预紧与突然卸载)等方面存在较大差异性。目前,针对该类型气动式大负载撞击试验装置,尚无关于其内弹道模型及性能影响因素的研究。针对某气动式大负载撞击试验装置[13],研究发射过程中各部件基本工作原理与相互关联,建立撞击试验装置的内弹道数学模型,并利用试验数据对模型进行验证。以该内弹道模型为基础,分析相关因素对发射性能的影响。所建立的内弹道模型较好地解决了速度范围适用性和预测精度的问题,可满足大质量装备公路、铁路、空运(速度在30～100 m/s)等典型事故撞击试验考核和研究,也可为同类试验技术和气体弹射装置设计提供参考。

1 撞击试验装置工作原理

撞击试验装置主要由高压气源、发射系统、一级制动系统、二级制动系统、轨道等构成,如图1所示。

1为定滑轮;2为缓冲块;3为滑轨;4为活塞;5为动力缸;6为往复车;7为承载小车及试验件;8为张紧绳;9为排气缸;10为张紧装置;11为控制系统;12为液压系统;13为高压气源;14为发射阀;15为一级制动系统;16为主牵引绳;17为二级制动系统图1 撞击试验装置示意图Fig.1 Sketch of the impact test facility

该试验装置的工作过程为:首先对高压气源充压,并安装、连接试验件。发射时,打开发射阀,高压气体经过发射阀进入气缸,达到一定值时,推动活塞—试验件加速运动,直至达到目标速度,活塞进入排气缸,一级制动系统制动活塞系统,试验件与活塞系统分离。发射完成后,复位系统将活塞系统复位。

在发射过程中,各部件的相互关系和工作原理如图2所示,当发射阀开启时,流通面积S从零开始增大,质量流Qm从高压气源流向气缸,Qm的大小由高压气源和气缸的压力PH、PL以及流通面积S决定;发射负载在气缸压力PL的作用下加速运动,使气缸的容积和试验件的行程l同时增大。

由图2可知,要建立撞击试验装置发射系统的数学模型,首先需建立高压气源、气缸的热力学模型、发射阀的流量方程、发射负载的动力学模型,然后通过对各部件间工作关系进行分析并组合,建立发射系统的内弹道模型。

2 内弹道模型的建立与验证

2.1 高压气源热力学模型

发射过程中,高压气源通过发射阀不断地给气缸提供高压气体。即在某一时刻高压气源中的气体从发射阀输出并放热,经过此过程后,高压气源在下一时刻达到新的平衡。假设气源的热力学过程为准静态过程,高压气源为刚性容器,可忽略压力和温度引起的体积变化,并忽略气体的摩擦损失,气体按理想气体考虑。由于发射系统的动作过程在约3 s,可认为储气筒放气过程是绝热等熵过程[20-22],则有

(1)

式(1)中:PH0、TH0分别为高压气源放气前的空气压力(绝对压力)、热力学温度;PH、TH分别为高压气源放气后t时刻的空气压力、热力学温度。

发射过程中,高压气源的高压气体通过发射阀流入气缸。高压气源放气过程的质量守恒[23]方程为

dmH=-Qmdt

(2)

式(2)中:mH为高压气源中的气体质量;dmH为从储气筒流出的气体质量;Qm为经过发射阀流出的气体质量流。

根据热力学第一定律,高压气源放气过程的能量守恒方程为

hdmH=-dUH

(3)

式(3)中:h为储气筒流出单位质量气体所带走的能量,即压缩空气的比焓;dUH为储气筒内气体内能的减少量。

对于理想气体,从高压气源流出的空气所带走的总能量可表示为

hdmH=cpTHdmH

(4)

式(4)中:cp为气体的定压热容。

高压气源空气内能的减少量可表示为

dUH=cvd(THmH)

(5)

式(5)中:cv为气体的定容热容。

根据理想状态方程,有

PHVH=mHRgTH

(6)

式(6)中:VH为高压气源的体积(为定值);Rg为空气的气体常数。

定压热容与定容热容之间的关系可表示为

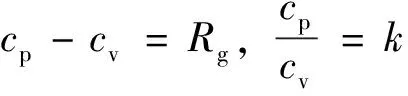
(7)

式(7)中:k为比热比。

联立式(2)～式(7),可得

(8)

2.2 气缸的热力学模型

在发射过程中,高压气源的气体经发射阀进入气缸,推动活塞,使试验件加速运动。假设气缸在发射过程的热力学过程为准静态绝热过程,并忽略压力和温度引起的体积变化以及气体的黏性作用。依据质量守恒、能量守恒的原理和气体的状态方程,结合气缸体积变化与活塞—试验件系统的运动关系,并考虑实际工作过程中气缸气体泄漏对能量的损失,即可建立气缸的数学模型。

由于气缸无法做到完全密封,高压气体流入气缸后必然存在一定的泄漏,因此,引入流量损失系数X,根据质量守恒,有

dmL=(1-X)dmH

(9)

式(9)中:mL为气缸内的气体质量;dmL为气缸内增加的有效气体质量。

根据热力学第一定律,气缸内气体的能量守恒方程[24]为

(1-X)hdmH=dUL+dW

(10)

式(10)中:等号左侧为从高压气源流入气缸的有效气体的总能量;dUL为气缸内气体内能的增加量;dW为气缸内气体体积膨胀所做的功。

对于理想气体,流入气缸的有效气体的总能量可表示为

(1-X)hdmH=(1-X)cpTHdmH

(11)

气缸内气体内能的增加量可表示为

dUL=cvd(TLmL)

(12)

式(12)中:TL为气缸内的气体热力学温度。

气缸体积变化所做的功可表示为

dW=PLdVL

(13)

式(13)中:PL为气缸内的气压(绝对压力);VL为气缸的容积,其表达式为

VL=A1(l0+l)

(14)

式(14)中:A1为气缸内牵引绳一侧的活塞面积;l0为活塞的初始位置(相对于气缸起始点);l为活塞的运动行程。

根据理想状态方程,有

PLVL=mLRgTL

(15)

联立式(7)、式(9)～式(15),可得

(16)

2.3 发射负载动力学模型

对发射负载进行受力分析,可知,发射负载在气缸的推力、空气阻力、摩擦力的共同作用下运动。结合气缸推力与气缸压力的关系,即可建立其动力学方程。

发射总负载me包含三部分,可表示为

me=m0+m1+m2

(17)

式(17)中:m0为活塞质量;m1为承载小车质量;m2为被试品质量。

根据牛顿第二定律,对于质量为me的总负载,运动过程中合外力F与加速度a的关系为

F=mea

(18)

负载在气缸的推力、空气阻力、摩擦力的共同作用下运动[25],因此可得

(19)

式(19)中:Pa为标准大气压力;A1为气缸的截面积;CD为空气阻力系数;A0为试验件迎风面积;ρa为标准大气空气密度;f为摩擦系数;v为负载的速度。

发射过程的运动学方程为

(20)

式(20)中:a为负载的加速度。

2.4 发射阀质量流量模型

高压气源与气缸两个热力学体系的之间的关联,就是发射阀的气体质量流。由于空气经发射阀阀口流动快,忽略壁面摩擦,可认为气体的流动为一维等熵流动(无摩擦绝热)。发射阀流量计算公式为[19,25-26]

(21)

2.5 内弹道模型验证

基于式(1)、式(8)、式(16)～式(21)的撞击试验系统的内弹道方程,采用四阶-五阶龙格库塔法进行系统仿真,其中气体及撞击试验系统的参数如表1[27-28]所示。

表1 气体及系统参数[27-28]

利用上述内弹道模型,开展了多个工况下(不同发射质量、发射气压)的发射速度预测,并与实测发射速度数据进行了对比,如表2所示。由结果可知,各种不同工况下,该理论模型最大误差为4.69%。总体来看,模型对于试验装置各个能力区间内的速度预测具有普适性。

表2 内弹道模型与实测结果对比

3 性能影响因素分析

撞击试验装置在发射过程中,相关因素的变化会对其内弹道性能带来影响。如,环境温度变化影响气源的能量,开阀时间会影响气源和气缸之间的流通的气体总质量,气缸中气体泄漏以及气体与气缸内壁的摩擦造成能量的耗损等等。因此,在所建立的内弹道模型基础上,以表2中工况7(大质量、高速工况)为例,以单一因素为变量,获得不同影响因素下(环境温度、开阀时间、气体耗损、摩擦阻尼、空气阻尼)内弹道性能的变化规律,为发射速度精度的控制以及同类型试验装置的设计提供参考。

3.1 环境温度对内弹道性能的影响

为分析环境温度对内弹道性能的影响,以气源温度为单一变量,将气源的初始温度分别设定为-40、-20、0、20、40 ℃,其他系统参数不变,分别给出了不同温度对气源压力、气缸压力和发射速度随行程的变化趋势,如图3所示。

图3 不同温度下气源、气缸压力和速度变化曲线Fig.3 Variation curve of air source pressure, cylinder pressure and launch velocity at different temperatures

由图3(a)可知,高压气源中的压力随行程呈现出指数型衰减的趋势,初始阶段的斜率较大,随着行程的增大,变化的趋势趋缓。这是由于发射阀开启后,气流迅速从高压气源进入气缸的初始空间,快速建立压力区,因此出现了明显的压降。而后,压力达到一定值后,活塞带动试验件开始运动,气缸的容积随活塞运动而增大,气源压力也随之减小。由图3(b)可知,气缸中的压力在行程较小时迅速增加,达到峰值后,以较快的速度下降,最终压力随行程的进一步增大而趋缓。这是由于在起始阶段,活塞的行程较小,气缸中增加的容积和初始容积相比是小量,所以在初始压力差较大的情况下,气缸中的压力增长较快,到达峰值后,气缸内、外的压差达到最大,活塞的加速度也到达峰值,随着时间的增长,活塞的速度及行程快速增长,气缸的容积也快速增大,其增长的速度超过了气体的增加的速度,气缸内的压力呈现快速下降并逐步趋缓的现象。由图3(c)可知,发射速度也呈现出在行程较小时快速变化,随着行程增大,发射速度变化趋缓的现象。

对比同一行程下,不同温度的高压气源、气缸压力和发射速度的变化情况可知,随着温度的增大,气源的压力变化也增大,-40 ℃时的初始和最终的压力变化为0.88 MPa,40 ℃的压力变化为0.95 MPa;气缸中,随环境温度的增大,气压上升的越快,-40 ℃时气缸的最大峰值为4.42 MPa,40 ℃时最大峰值为4.67 MPa,斜率分别为1.24和1.43;发射速度与温度正相关,同一行程下,温度越高,发射速度越大,-40 ℃时最大速度为86.8 m/s,40 ℃时最大速度为89.82 m/s,相对增加了3.2 m/s(相对增大3.5%)。

3.2 开阀时间对内弹道性能的影响

为分析发射阀开阀时间对内弹道性能的影响,分别选取开阀时间为0.4、0.8、1.2、1.6、2.0 s进行研究。图4给出不同开阀时间下气源压力、气缸压力、速度随行程的变化曲线。

图4 不同开阀时间下气源、气缸压力和速度变化曲线Fig.4 Variation curve of air source pressure, cylinder pressure and launch velocity at different valve opening times

由图4(a)可知,不同开阀速度下,高压气源中的压力随行程基本呈现出指数型衰减的趋势,起始阶段的斜率与开阀时间密切相关,开阀时间越大斜率越小,随着行程的进一步增大,变化趋缓。开阀时间为0.4 s时,最大行程下(75 m)气源的压力为4.72 MPa,开阀时间为2 s,气源的最终压力为4.81 MPa。可知,同一行程下,随着开阀时间的增大,高压气源的压力变化减小,这是由于开阀时间越长,从气源中流出的气体就越少。由图4(b)可知,气缸中的压力呈现先快速增大,再以较快的速度减小,然后随行程进一步增大变化而趋缓。同一行程下,气缸内的气压幅值差异较大,起始阶段,随开阀时间的增大,气缸的气压增长越慢,开阀时间为0.4 s时,气缸的最大峰值为4.59 MPa,斜率为1.28,开阀时间为2 s时,最大峰值为2.74 MPa,斜率为0.29。由图4(c)可知,同一行程下,不同的开阀时间对发射速度影响较大,开阀时间越大,发射速度越小,开阀时间为0.4 s,速度为89.3 m/s,开阀时间为2 s时,速度为78.9 m/s,相对减小了11.6%。

3.3 气体耗损对内弹道性能的影响

为研究气体耗损对内弹道性能的影响,分别取流量损失系数为0.2、0.3、0.4、0.5、0.6,分析其对气源压力、气缸压力和发射速度的影响规律。图5给出了不同损失系数下气源压力、气缸压力、发射速度随行程的变化曲线。

对比同一行程下,不同损失系数下的气源压力、气缸压力和反射速度的变化情况可知,随着气体耗损的增大,气源的压力变化也增大,损失系数为0.2时,气源的压力变化为0.75 MPa,损失系数为0.6时,气源的压力变化为1.01 MPa。气缸中,损失系数越大,压力峰值越小;起始阶段,损失系数越大,气缸中的气压上升的越慢;损失系数为0.2时,气缸的最大峰值为5.27 MPa,斜率为1.22,损失系数时间为0.6时,最大峰值为2.24 MPa,斜率为0.62。发射速度随损失系数的增大而减小;损失系数为0.2时,最大发射速度为100.5 m/s,损失系数为0.6时,最大发射速度为85.1 m/s,相对减小了15.3%。

3.4 摩擦、空气阻尼对内弹道性能的影响

分别以摩擦系数和空气阻尼系数为单一变量,分析其对内弹道性能的影响,其中,摩擦系数取为0.05、0.1、0.15、0.2、0.25,空气阻尼系数取为0.15、0.3、0.45、0.6、0.75。图6、图7给出了不同摩擦系数和空气阻尼系数下气源压力、气缸压力、速度随行程的变化曲线。

图6 不同摩擦系数下气源、气缸压力和速度变化曲线Fig.6 Variation curve of air source pressure, cylinder pressure and launch velocity at different friction coefficients

图7 不同空气阻尼下气源、气缸压力和速度变化曲线Fig.7 Variation curve of air source pressure, cylinder pressure and launch velocity at different air damping coefficients

对比同一行程下,不同摩擦和阻尼系数下的气源压力、气缸压力和反射速度的变化情况可知,随着摩擦系数和阻尼系数的增大,高压气源、气缸中的压力变化基本相同,发射速度变化较小,摩擦系数从0.05变为0.25,速度只减小了0.11 m/s(相对减小0.1%),空气阻尼系数从0.15变为0.75,速度只减小了0.31 m/s(相对减小0.3%),影响基本可忽略。

4 结论

根据某气动式撞击试验装置的工作原理,建立了内弹道数学模型,开展多个工况下(不同发射质量、发射气压)的发射速度预测,并与实测数据进行了对比;利用该模型,以单一因素为变量,研究不同影响因素下(环境温度、开阀时间、气体耗损、摩擦阻尼、空气阻尼)内弹道的变化规律,得出如下结论。

(1)建立的理论模型对于速度在30～100 m/s、总负载在1 500～9 000 kg范围内的预测精度较高,最大发射速度误差在5%以内,对于各种不同的工况具有较好的普适性。

(2)随着环境温度的升高,气源的压力变化增大,气缸气压上升速率加快,发射速度越大,40 ℃下发射速度相对于-40 ℃增加了3.5%。

(3)随着开阀时间的增大,气源的压力变化减小,气缸的气压增长越慢,发射速度越小,开阀时间为2 s的发射速度相对于开阀时间为0.4 s的速度减小了11.6%。

(4)随着气体耗损的增大,气源的压力变化增大,气缸气压增长越慢,损失系数为0.6时发射速度相对于损失系数为0.2的速度减小了15.3%。

(5)不同摩擦和阻尼系数对气源压力、气缸压力和反射速度的变化影响较小,摩擦系数从0.05变为0.25,速度只减小了0.1%,空气阻尼系数从0.15变为0.75,速度只减小0.3%,影响基本可忽略。