裂缝交叉角度对缝网导流能力的影响:以“卜”形结构为例

刘加杰, 宁文祥, 王鹏, 车永新, 何柏,3*

(1.四川省非金属(盐业)地质调查研究所, 自贡 643021; 2.四川大学新能源与低碳技术研究院, 成都 610207;3.四川大学后续能源材料与器件教育部工程研究中心, 成都 610065)

利用水力压裂技术对高致密、超低渗的页岩储层进行压裂增渗,是实现页岩气有效开采的必要手段[1]。随着压裂技术与理论的发展,在人工干预与储层非均质特性综合影响下,人工压裂主裂缝扩展的同时在侧面产生多级侧枝次生裂缝,多级次生裂缝进一步延伸与天然裂缝相互作用,最终形成多级人工裂缝与天然裂缝交错连接的复杂裂缝网络[2-3]。另一方面,由于裂缝宽度、形态等差异,支撑剂难以在裂缝网络中均匀铺置,储层中不同铺置浓度的支撑型裂缝与剪切滑移形成的自支撑裂缝共同形成了复杂的油气渗流通道[4-5],其综合导流能力是评价压裂施工效果、决定页岩气高效开发的重要参数[6-9]。

目前,利用美国石油协会(American Petroleum Institute,API)标准导流室开展支撑剂种类、粒径、铺置浓度、铺置方式等对单裂缝短期/长期导流能力的影响已开展了大量的研究[10-16],为油气资源开发提供了重要的理论与技术支撑。而针对页岩气储层改造后所形成的复杂裂缝网络的导流能力评价尚处于初期探索阶段[17];复杂裂缝网络中流体由次生裂缝汇流到主裂缝时发生碰撞、混掺导致部分能量损失,且流体流量越大,因碰撞、混掺损失的能量也越多[18];且当裂缝交错的连接点缺乏有效支撑时,在闭合应力作用下,交错裂缝极易失去连通性,进而降低裂缝网络的导流能力[19]。因此,利用单裂缝导流能力试验难以有效准确评价裂缝网络的导流能力。温庆志等[20-21]将复杂缝网结构抽象为主裂缝与次生裂缝垂直相交的基本单元,如“T”形、“十”形、“丰”形等,结果表明,次生裂缝数量越多,缝网导流能力越大,但缝网导流能力随闭合压力升高的衰减幅度也随之增大。然而,裂缝网络并非完全由一系列正交裂缝组合而成,交错裂缝的夹角可能呈任意角度[22-23]。刘日成等[24-25]利用透明玻璃构建了非正交裂缝网络物理模型,探讨了流体在非正交裂缝网络中的流动规律。李凤霞等[26]认为,次生裂缝对称分布于主裂缝两侧,探讨了裂缝夹角为30°、45°、60°和90°时缝网结构的导流能力,结果表明,缝网导流能力随次生裂缝与主裂缝夹角减小而增大,且缝网导流能力越大,其随着闭合压力升高而降低的幅度也越高。

页岩水力压裂后,页岩气由基质析出后,沿着天然裂缝、多级次生裂缝经主裂缝流向管井开采利用,由于页岩气运移路径复杂,而不同位点的裂缝导流能力并不完全一致,任意薄弱环节都将影响页岩气的高效开发;此外,由于流体在交错点汇流时导致的能量损失与裂缝间夹角密切相关,正交型与对称型缝网单元并不能完全反映缝网的真实情况,亟需针对普适性更强的缝网单元开展导流能力研究。水力压裂裂缝形态表明[3],水力改造形成的树枝状裂缝可以视为一系列不同角度的“卜”形结构交叉裂缝组合形成,因此,以“卜”形交叉裂缝单元为基础,系统探讨裂缝交叉角度、铺置浓度等对缝网导流能力的影响,以期能为缝网导流能力准确评估奠定基础,进而为压裂施工参数优化设计提供支撑。

1 试验方法与试验方案

1.1 试验装置与岩板尺寸

将硬质橡胶加工成外圆内方的结构用以模拟“卜”形交叉裂缝导流室,其橡胶套筒外部直径为100 mm,高度120 mm,橡胶套筒内部方形空腔横截面尺寸为60 mm×60 mm,利用线切割将橡胶套筒沿对称轴切开,其半块形状如图1所示,以方便岩板安装、支撑剂铺设等。将加工好的岩板安装到橡胶套筒内,如图2(a)所示,为了避免岩板2与套筒贴合过紧影响渗流介质流动,在岩板2与套筒间铺设1层钢丝网形成渗流通道,在其他岩块与橡胶套筒接触部位利用软橡胶填充,以确保渗流介质沿预定路径运移,如图2(b)所示。利用热缩膜包裹橡胶套筒导流室和上、下渗流压头,以防止围压油进入试样,并将其整体置于TOP2518岩石综合力学试验系统中,如图3所示,采用常规液体稳态法测量“卜”形交叉裂缝网络渗流特性,渗流介质采用高纯水。

图1 外圆内方橡胶套筒导流室Fig.1 Rubber sleeve with the outer circle and the inner square configuration as fracture conductivity chamber

虚线表示裂缝;黑色箭头表示受力;红色箭头表示测试流体渗流方向;σ1为轴压; σ2为围压;θ为主/次生裂缝交叉角度图2 “卜”形交叉裂缝导流能力试验示意图Fig.2 Schematic diagram of “卜” type fracture network conductivity

图3 TOP岩石综合力学试验系统Fig.3 Rock mechanics testing system produced by TOP industry

将主裂缝与次生裂缝交叉点设置在岩板中心点处,通过调整3块岩板厚度尺寸使得次生裂缝长度不随主裂缝与次生裂缝夹角改变而变化。如图4所示,由岩板间的几何关系不难得到次生裂缝长度n与岩板3的厚度d之间的关系可表示为。

图4 “卜”形交叉裂缝岩板尺寸与受力示意图Fig.4 Sample size and schematic diagram of stress with“卜”fracture network

(1)

式(1)中:θ为主裂缝与次生裂缝的夹角,(°);l为次生在试样高度方向的投影长度,mm。

由于套筒空腔尺寸为60 mm,并结合式(1),所采用的岩板尺寸如表1所示,其加工完成的岩板实物如图5所示。

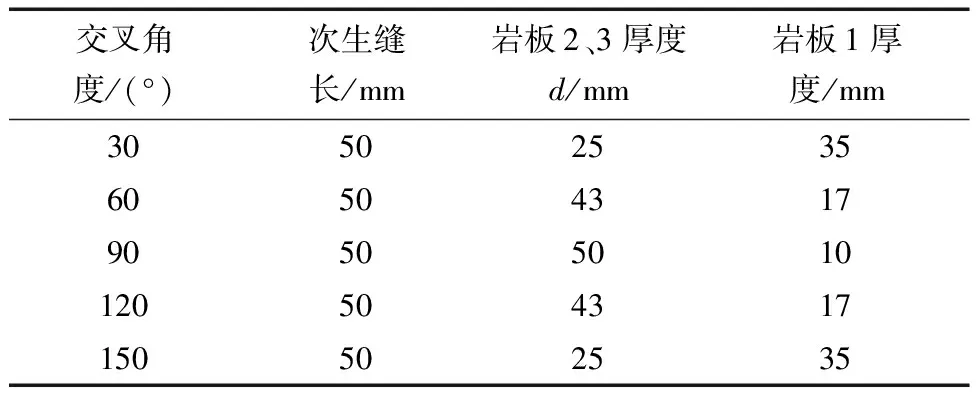
表1 不同交叉角度岩板尺寸

图5 “卜”形交叉裂缝试样岩板实物图Fig.5 Experimental samples with “卜”type configuration

1.2 “卜”形交叉裂缝导流能力测试原理

岩板构成的“卜”形交叉裂缝的渗流方向与受力状态如图3所示。主缝的闭合应力为围压值,而分支缝的闭合应力由轴压和围压两者共同决定,当θ= 90°时,次生裂缝的闭合应力等于轴压值,对于任意角度次生裂缝,其闭合应力的计算公式为

(2)

常规单裂缝导流能力表示为裂缝宽度与支撑带渗透率的乘积,由于多裂缝并不只有一条裂缝,裂缝宽度无法直接确定。为了解决这个问题,温庆志等[20-21]提出了裂缝体积等效法,即将裂缝网络中的裂缝总体积通过平行于渗流方向单缝的形式进行等效,从而计算出裂缝宽度;假设裂缝网络内总裂缝体积为V,将总的裂缝体积视为一条平行于渗流方向的单裂缝形成的裂缝体积,则该单裂缝在渗流方向上的面积为S,等效缝宽wf可表示为

(3)

由于液体在裂缝内流动属于层流,满足达西定律,其裂缝网络的渗透率kf可由式(4)得到。

(4)

式(4)中:kf为裂缝网络渗透率,cm2;Q为通过裂缝网络的流量,cm3/s;μ为测试流体黏度,Pa·s;L为平行于渗流方向的等效裂缝长度,cm;h为平行于渗流方向的等效裂缝高度,cm;wf为平行于渗流方向的等效裂缝宽度,cm;ΔP为裂缝网络进出口两端压力差,Pa。

1.3 试验方案

所用岩板取自重庆市彭水苗族土家族自治县鹿角镇志留系龙马溪组的页岩露头,利用切割、打磨等方式将其加工成表1与图4所示的岩板尺寸,其主裂缝与层理面平行;由于该地区页岩的各向异性特性较低[27],故而本试验不考虑其各向异性的影响。通过X射线衍射(X-ray diffraction,XRD)对其矿物成分分析可得该页岩主要矿物为石英、钠长石与白云母,其相对含量分别为46%、31%与23%。由于目前页岩气藏埋深大多超过3 500 m[28],因此,选用高强球形陶粒做支撑剂,该支撑剂抗压强度约为52 MPa,体积密度为1.65 g/cm3。由式(2)可知,当导流室处于静水压状态时,次生裂缝所受到的闭合应力与主裂缝闭合应力相同,并均等于围压。为了避免主、次生裂缝因闭合应力的不同而导致导流能力改变,本试验主要在静水压状态下探讨裂缝交叉角度、支撑剂铺置浓度、闭合应力、主/次生裂缝铺置浓度差异等对“卜”形裂缝导流能力的影响,其具体的试验方案如表2所示。

表2 “卜”形交叉裂缝导流能力试验方案

2 试验结果与讨论

2.1 支撑剂铺置浓度对“卜”形交叉裂缝导流能力的影响

与常规单裂缝导流能力相似,无论交叉角度如何变化,支撑剂充填的支撑型裂缝导流能力远高于无支撑剂充填的自支撑裂缝导流能力,且“卜”形交叉裂缝导流能力随着闭合应力的升高而逐步降低,如图6所示。以交叉角度为90°为例,当闭合应力由20 MPa升高至60 MPa时,铺置浓度为1.0/1.0、2.0/2.0、3.0/3.0 kg/m2的“卜”形交叉裂缝导流能力分别降低了33.7%、22.6%和24.1%。由图6可知,当支撑剂铺置浓度为1.0/1.0 kg/m2时,随着闭合应力的升高,交叉裂缝导流能力的降低幅度逐渐增大;当铺置浓度为2.0/2.0 kg/m2时,裂缝导流能力随闭合应力升高近似呈线性降低;而当铺置浓度为3.0/3.0 kg/m2时,裂缝导流能力在闭合应力为30～50 MPa时基本保持不变,且在高闭合应力作用时具有最高的导流能力。

以1.0/1.0为例,表示主裂缝与分支裂缝支撑剂铺置浓度分别为1.0、1.0 kg/m2;30°、90°、150°为交叉角度图6 不同支撑剂铺置浓度对“卜”形交叉裂缝导流能力的影响Fig.6 Effect of the proppant concentration on the “卜”fracture network conductivity

相同交叉角度下闭合应力小于50 MPa时,交叉裂缝导流能力随铺置浓度的升高先降低后升高,这主要是由于支撑剂为1.0/1.0 kg/m2时,根据支撑剂体积密度为1.65 g/cm3,每平方厘米裂缝中支撑剂体积约为0.06 cm3,而20目支撑剂的粒径约为0.84 mm,其每平方厘米所形成的空间为0.084 cm3;因此,当支撑剂铺置浓度为1.0/1.0 kg/m2时,支撑剂难以将整个裂缝紧密填充,支撑剂与支撑剂之间的空隙为流体提供了良好的渗流空间,因此当铺置浓度较低时交叉裂缝具有更好的导流能力。然而当闭合应力接近50 MPa时,因支撑剂强度约为52 MPa,此时部分支撑剂在高闭合应力作用下开始破裂,进而交叉裂缝导流能力急剧下降。可见增大裂缝内支撑剂铺置浓度、提高支撑剂的抗压强度对于确保支撑体系的可靠性、提升交叉裂缝的导流能力具有重要意义。

2.2 交叉角度对“卜”形交叉裂缝导流能力的影响

为了探究交叉角度对裂缝导流能力的影响,固定支撑剂铺置浓度为2.0 kg/m2分别开展单裂缝与交叉角度为30°、60°、90°、120°、150°的交叉裂缝的渗流特性试验,其测得的导流能力如图7所示。可以看出,存在次生裂缝的“卜”形交叉裂缝导流能力明显高于单裂缝导流能力,但两者随闭合应力升高的衰减规律无显著差异。当闭合应力由20 MPa升高至60 MPa时,交叉角度为30°、60°、90°、120°、150°的“卜”形裂缝导流能力分别降低了23.4%、24.3%、22.6%、23.1%、21.7%,而单裂缝导流能力降低25.6%。可见,无论主裂缝与次生裂缝的夹角如何,相较于单裂缝,“卜”形裂缝导流能力对闭合应力的抵抗能力无显著增强。

图7 闭合压力对“卜”形裂缝导流能力的影响Fig.7 Effect of the closure stress on the “卜” fracture network conductivity

以铺置浓度为2.0 kg/m2单裂缝导流能力为基准条件,在相同闭合应力条件下,以不同交叉角度“卜”形裂缝导流能力除以单裂缝导流能力,可得到因次生裂缝存在导致的导流能力提升百分率,如表3所示。相同闭合应力条件下,“卜”形交叉裂缝的导流能力较单裂缝提升约18.02% ～ 30.62%。这是因为与单裂缝相比,“卜”形交叉裂缝增加了次生裂缝,测试流体可以同时由次生裂缝和主裂缝流入“卜”形交叉裂缝,次生裂缝就会发挥分流作用。而根据达西定律可知,流体水头损失梯度与流量呈正相关,当总流量不变时,次生裂缝会降低单裂缝的流量,从而减少水头损失。虽然流体在交叉点处汇流时,流体碰撞会引起水头损失变大,但是流体碰撞增大的水头损失小于分支裂缝分流作用所减小的水头损失。因此,在相同流量下,增加次生裂缝会使“卜”形交叉裂缝内水头损失减小,最终导致裂缝网络导流能力的增加。

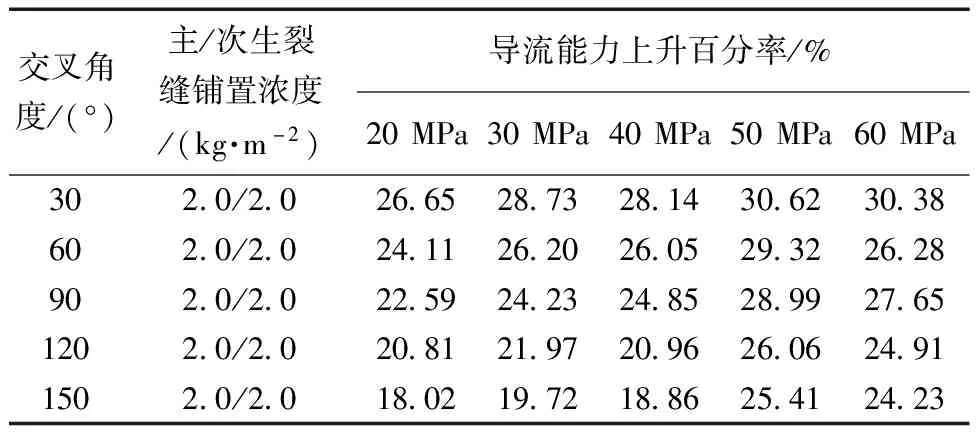
表3 不同角度“卜”形裂缝的导流能力提升百分比

如图8所示,在相同闭合应力条件下,随着交叉角度的增大,“卜”形裂缝导流能力提升幅值逐渐降低,这一规律与文献[26]相似,也侧面印证了所采用方法的可靠性。以闭合应力20 MPa为例,交叉角度由30°增至150°,其导流能力提升幅值由26.65%下降至18.02%;这主要是由于高交叉角度情境下,次生裂缝中的流体与主裂缝流体在交叉点汇合时流体发生对撞造成局部紊流导致能量损失相较于低交叉角度更高。因此,在评价缝网导流能力时,需充分考虑流体汇流角度导致的能量损失差异。

图8 交叉角度对“卜”形裂缝导流能力的影响Fig.8 Effect of the interaction angle on the “卜” fracture network conductivity

2.3 主/次生裂缝铺置浓度不同对“卜”形交叉裂缝导流能力的影响

页岩储层中,主裂缝中的支撑剂铺置浓度往往大于次生裂缝。因此,在“卜”形裂缝中保持主裂缝铺置浓度为3.0 kg/m2不变,次生裂缝中的铺置浓度分别为1.0、2.0、3.0 kg/m2,进而探究因主、次生裂缝中铺置浓度差异导致的交叉裂缝导流能力变化规律,并与铺置浓度为3.0 kg/m2的单裂缝导流能力对比,具体的试验方案如表2所示。以铺置浓度为3.0 kg/m2单裂缝导流能力为基准条件,在相同闭合应力条件下,以不同交叉角度或铺置浓度的“卜”形裂缝导流能力除以单裂缝导流能力,可得到因次生裂缝存在导致的导流能力提升百分率,如表4所示。由表4可知,无论次生裂缝的铺置浓度、交叉角度如何变化,次生裂缝存在均会提高裂缝的导流能力,其提高幅度为16.67%～42.52%。因此,在储层改造过程中增强裂缝网络复杂性有利于获得更好的导流能力。

表4 不同交叉角度、次生裂缝铺置浓度的“卜”形裂缝的导流能力提升百分比

对比图6与图9可知,当次生裂缝铺置浓度为大于2.0 kg/m2时,“卜”形裂缝导流能力随闭合应力的变化规律与铺置浓度3.0 kg/m2相似,表明具有高铺置浓度的裂缝在高闭合压力作用下可保持较为稳定、可靠的导流能力。而当主、次生裂缝铺置浓度为3.0/1.0 kg/m2与的“卜”形交叉裂缝导流能力随闭合应力的变化规律与铺置浓度为1.0/1.0 kg/m2时相似,即在高闭合应力作用下,其导流能力快速降低。当主裂缝支撑剂铺置浓度相同时,次生裂缝的导流能力决定了裂缝网络的导流能力大小。因此,增强支撑剂自身抗压强度,提高次生裂缝中支撑剂铺置浓度,有利于提升裂缝网络在高闭合应力下的有效性。

30°、90°、150°为交叉角度;以3.0/1.0 kg/m2为例,表示主裂缝与分支裂缝支撑剂铺置浓度分别为3.0、1.0 kg/m2图9 主/次生裂缝铺置浓度不同对“卜”形交叉裂缝导流能力的影响Fig.9 Effect of proppant concentration in the primary and secondary fracture on the “卜” fracture network conductivity

3 结论

以“卜”形交叉裂缝结构为裂缝网络基本单元,系统探讨了裂缝交叉角度、支撑剂铺置浓度等对裂缝导流能力的影响,试验结果将对页岩储层水力压裂改造后缝网导流能力准确评估提供较好的指导意义,通过试验研究与分析得出以下结论。

(1)提升裂缝中支撑剂铺置浓度,尤其是分支裂缝中的支撑剂浓度,降低支撑剂破碎率,均有利于裂缝网络在高闭合应力中保持稳定、高效的导流能力。

(2)闭合应力由20 MPa升高至60 MPa时,交叉角度为30°、60°、90°、120°、150°的“卜”形裂缝导流能力分别降低了23.4%、24.3%、22.6%、23.1%、21.7%,而单裂缝导流能力降低25.6%。可见,无论主裂缝与次生裂缝的夹角如何,“卜”形裂缝导流能力对闭合应力的抵抗能力无显著增强。

(3)次生裂缝中支撑剂的铺置浓度往往决定了缝网导流能力-闭合应力之间的变化趋势;然而,无论次生裂缝中支撑剂铺置浓度如何,次生裂缝可降低流体流动过程中的压力损失,进而拥有比单裂缝更高的导流能力,因此,尽可能形成复杂的裂缝网络有利于提升储层的导流能力。

(4)流体汇流角度越大,因流体碰撞而造成的能量损失也越大,故而“卜”形裂缝导流能力随交叉角度增大而减小;因此,在讨论裂缝网络导流能力的时候,必须充分考虑流体汇流时的交叉角度。