基于电磁层析成像的钢轨探伤传感器设计与优化
付成凯
(中铁十八局集团有限公司,天津 300222)
铁路的迅速发展给人们的生产和生活提供了巨大便利,然而随着铁路行业的迅速发展,列车安全与稳定问题也越发引起重视。钢轨是铁路系统的重要组成部分,其损伤的检测与定位对列车运行安全至关重要。常见钢轨探伤手段有超声(Ultrasound)[1]、机器视觉(Machine Vision)[2]、漏磁(Magnetic Fluxleakage Testing,MFL)、涡流(Eddy Current Testing,ET)[3]、电磁层析成像[4]。电磁层析成像技术具有可视化的优点,成本低廉,可用于表面和浅表面损伤的动态或固定周期检测。在电磁层析成像技术研究中,传感器的设计与优化是一个关键问题,必须予以重视。
1 电磁层析成像传感器相关研究
传感器结构中,多相流检测的传感器结构最为典型[5],其结构如图1所示。此类传感器结构被称为全包围结构或“O”型结构,传感器线圈均匀分布于管道外,其特点是灵敏度矩阵分布轴对称,线圈对管道中心区域的敏感性稍弱。这类结构还可应用于液态金属流型检测中,但无法应用于金属损伤检测中,更不必说应用于复杂的钢轨损伤检测中。
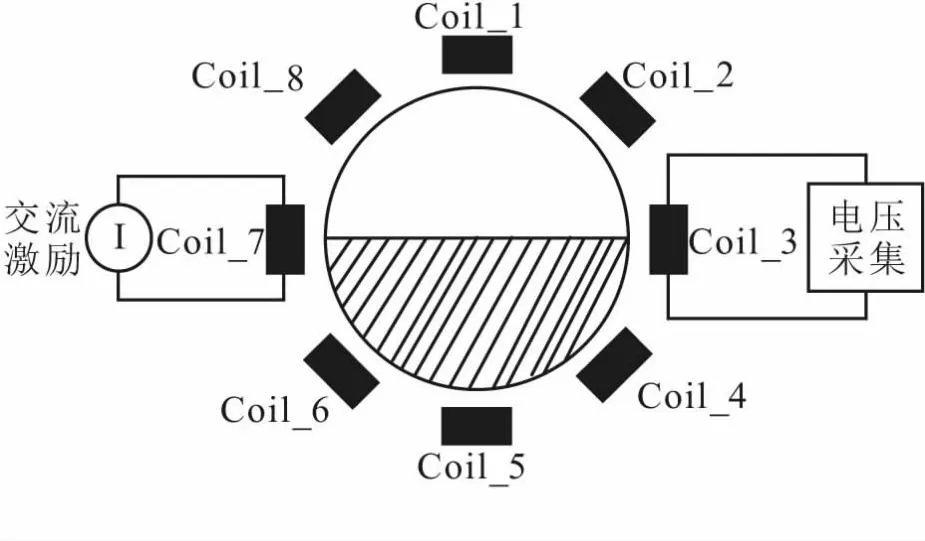
图1 电磁层析成像传感器的典型结构
为解决金属损伤检测中传感器结构不匹配问题,倒“L”型结构[6]和平板式结构[7]被提出,其结构如图2所示。这两种传感器阵列排布方式适用情况不同,倒“L”型结构适用于被测对象有明显拐角的情况,平板式结构适用于被测对象为平面、损伤检测区域在表面或浅表面的情况。这两种传感器结构可应用于钢轨局部的损伤检测,当损伤检测区域需要继续扩大或者被测对象为完整钢轨模型时,这两种传感器结构就有些捉襟见肘,因此亟需设计一种全新的传感器结构。
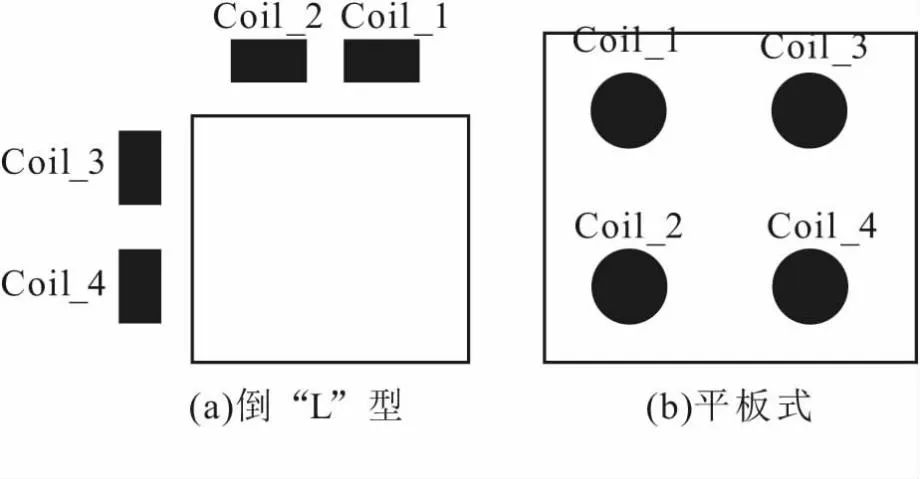
图2 传感器结构
传感器参数优化是标准的复合参数优化或多参数优化问题,多参数优化问题解法有正交实验法、神经网络法和混沌模拟退火粒子群算法等方法。正交实验法是研究复合参数多水平的一种方法,它依据 Galois理论从全面实验中挑选出部分具有代表性的水平组合进行实验,这些组合在全面实验中均匀分布,可以反映出各参数变化对结果的影响,因此对结果进行分析就可以找出最优的水平组合[8]。其优点是实验次数少,可信程度较高,当参数较多时,能利用少量实验得出较为合理的结论。神经网络法则是利用神经网络解决最优化问题,利用多组已知数据对神经网络进行优化,实现传感器设计参数与模型优化函数匹配,其优点是在模型不变的情况下,神经网络法获得的结果更为精准,但是所需实验次数较多,在模型复杂时会消耗大量时间[9]。粒子群算法是一种基于群体协作的随机搜索算法,具有搜索速度快、效率高、算法简单等优势,但该方法对于有多个局部极值点的函数,容易陷入到局部极值点中,得不到正确的结果,常用于解决多目标优化问题[10]。
2 电磁层析成像理论基础
参考文献[11],以数学方式描述电磁层析成像正问题中电导率或磁导率与检测电压的关系:

(1)
式中:V为检测电压;σ(x,y)和μ(x,y)分别为电导率和磁导率的分布。以电导率分布的计算为例,公式(1)可以简化成式(2):
V=F(σ)
(2)
在基于线性假设的前提下,可认为电导率的微小扰动与电压在局部具有线性关系,可以得到式(3):
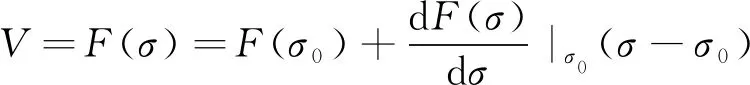
(3)
经过变换,可以得到检测电压偏差与电导率微小扰动的关系,如式(4):
ΔV=S(σ)·Δσ
(4)
式中:S(σ)为检测电压关于电导率微小扰动的导数。对电压测量值和电导率归一化后便可以得到如式(5)所示的常见公式:
U=S·g
(5)
式中:向量U为归一化电压偏差;向量g为归一化电导率偏差;向量S为灵敏度矩阵。
3 传感器设计与优化方法
3.1 钢轨探伤模型建模
钢轨是钢轨探伤模型的基础和对象,根据每米大致的重量,可以分为起重机轨、重轨和轻轨。课题研究的钢轨模型基于50 kg/m重型钢轨尺寸,钢轨高度152 mm,头部截面宽度70 mm、高度为42 mm,腰厚度为15.5 mm、高度83 mm,底部截面宽度为132 mm、高度27 mm。
对于钢轨,磁导率μ=4π×10-7H/m,电导率σ=1.137×106S/m,具有高电导率和高磁导率特性,在常用的频率范围1 kHz~1 MHz内,趋肤深度小于2.5 mm,设定浅表面损伤深度不超过2.5 mm。
由于完整钢轨模型结构复杂,传统“O”型传感器、平板型传感器阵列不再适用,本文以完整钢轨模型作为被测对象,以倒“L”型结构为参考,依据给出的传感器设计参数设计了如图3所示的传感器阵列形式。
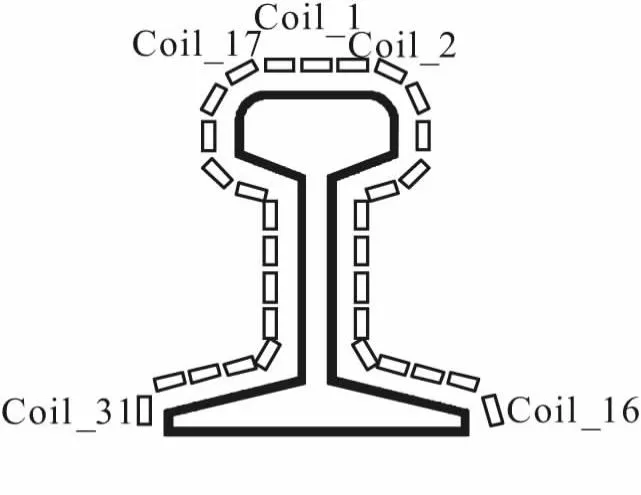
图3 传感器阵列排布结果
其中,传感器设计需要考虑以下参数:线圈传感器内径和外径、线圈与钢轨间距、线圈组间距、线圈匝数。初步选取传感器设计参数:线圈与钢轨表面的间距为10 mm,线圈组间距为16 mm,线圈内径为6 mm、外径12 mm,匝数为400,绕制线圈所用漆包铜线直径为0.18 mm,漆包线直径0.20 mm,以此初始参数进行钢轨探伤模型下探伤效果的验证。
3.2 图像重建验证
为验证基于电磁层析成像技术的钢轨探伤模型的正确性,选取了几种损伤模型进行图像重建,同时选取了LBP算法、Tikhonov正则化算法、截断奇异值分解算法分别对九种损伤情况进行图像重建。各个损伤模型在钢轨的分布如图4所示。
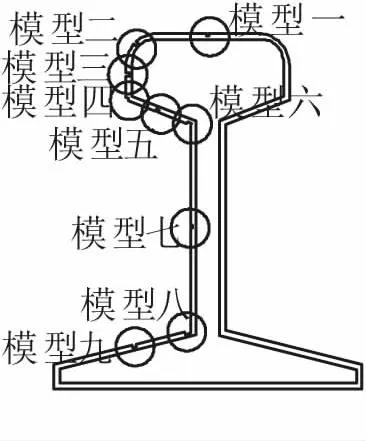
图4 钢轨九种损伤的分布
为进一步说明在不同损伤情况下各图像重建算法的优劣性,从而选用合适图像重建方法作为传感器优化的评价标准。本文使用了两个指标来评价重建图像与被测对象分布的匹配程度,分别是图像误差(image error)IE、图像相关系数(correlation coefficient)CC:
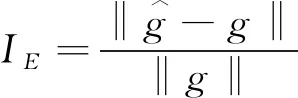
(6)
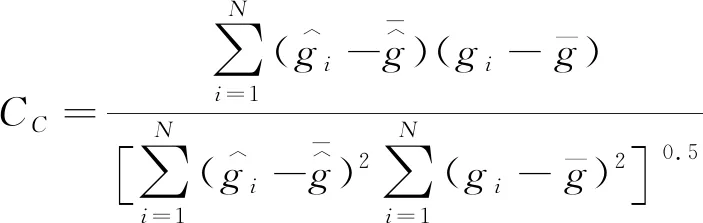
(7)
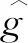
3.3 传感器参数优化
3.3.1 灵敏度矩阵均匀性指标
参考文献[8]提出灵敏度均差和标准差定义,分别定义电磁层析成像中灵敏度矩阵的均差(average deviation)Sad和标准差(standard deviation)Ssd:
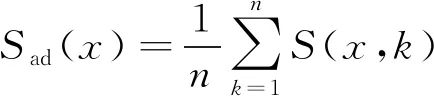
(8)

(9)
式中:S(x,k)为灵敏度矩阵第x行、第k列元素;n为钢轨探伤模型可检测区域定义的损伤数目,此式中为3 914。对其作均差,可以得到第x行对应线圈组的灵敏度均值Sad(x),这一均值越大,可认为该线圈组对损伤可检测区域的平均检测效果越强。标准差Sad(x)越小,说明该线圈组对可检测区域的损伤检测效果趋于一致。定义一个函数P(x):
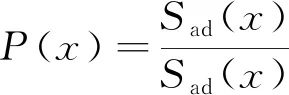
(10)
式中:P(x)为灵敏度均值和标准差的比值向量。定义一个标量值P,为灵敏度矩阵均匀性函数:
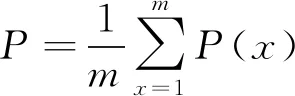
(11)
式中:m为检测电压独立测量值个数,不同传感器结构m一般不同。P越小,说明模型的灵敏度矩阵在敏感场分布越均匀。
3.3.2 灵敏度矩阵条件数指标
电磁层析成像逆问题本质是灵敏度矩阵的逆矩阵求解过程,是个病态问题。病态性影响逆问题中图像重建的误差。逆矩阵求解的病态程度与灵敏度矩阵条件数相关联,灵敏度矩阵条件数:
K=‖S‖×‖S-1‖
(12)
式中:‖S‖为灵敏度矩阵范数;‖S-1‖为灵敏度矩阵逆矩阵的范数,这两个范数通常选取2范数。由于电磁层析成像逆问题具有非线性和软场效应难题,灵敏度矩阵实现了电磁层析成像逆问题的局部线性化,在此范围内求解逆问题,局部线性拟合程度较好,解的精准度较高。当灵敏度矩阵条件数越大,灵敏度矩阵逆矩阵抗干扰能力越差,局部线性化所带来的误差越不可以忽略,解越不精确,从而导致图像重建效果变差。因此,灵敏度矩阵条件数越大,检测线圈电压值的微小偏差就会越影响损伤定位效果,模型抗干扰能力更弱。为减弱逆问题的病态程度,希望灵敏度矩阵的条件数越小越好。
3.3.3 模型优化函数
结合灵敏度矩阵均匀性和条件数两大指标,定义模型优化函数G,定义G越大,模型损伤检测效果越好,模型更优。
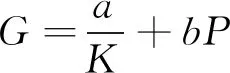
(13)
式中:a和b为权重参数,可由单一参数优化过程的先验信息计算获得。单一参数优化过程作为复合参数优化过程的正演,提供了优化标准的权重占比等先验信息,计算可采用线性拟合等方式。单个参数实验过程使用两种方法作为对比:第一种方法为优化标准对比,用于说明传感器设计参数改变时,各优化标准和模型优化函数的变化。第二种方法为图像重建效果对比,选取5种不同的损伤模型,改变传感器设计参数并对这5种损伤进行图像重建,进行结果比较。这一过程有两个目的:一方面是为了确定改变传感器设计参数后,钢轨探伤模型能否仍能对损伤进行图像重建,钢轨探伤模型是否仍然有效;另一方面是为了对比不同传感器设计参数下的图像重建效果,验证钢轨探伤模型优化函数与重建结果的相关性。单一参数优化最终得出:
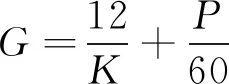
(14)
3.3.4 参数优化方案
本文对4个传感器设计参数进行优化,这4个参数对传感器设计影响较大,也是最显而易见的设计参数,分别为线圈与钢轨间距、线圈组间距、单个线圈内外径和线圈匝数。首先使用控制变量法进行单一参数优化,分析单个参数改变对灵敏度矩阵条件数、灵敏度矩阵均匀化这两个优化标准的影响,以此计算模型优化函数,并通过损伤模型的图像重建效果验证模型优化函数G正确性。
分析完单个传感器设计参数对钢轨探伤模型的影响,就需要从初始设计参数出发,进行复合参数优化,选取正交实验法作为复合参数优化方法,减少实验次数,获得最优传感器设计参数。
4 钢轨探伤模型建模与优化
4.1 损伤图像重建结果
对图4分布的九种损伤分别进行图像重建,图像重建结果如表1所示。
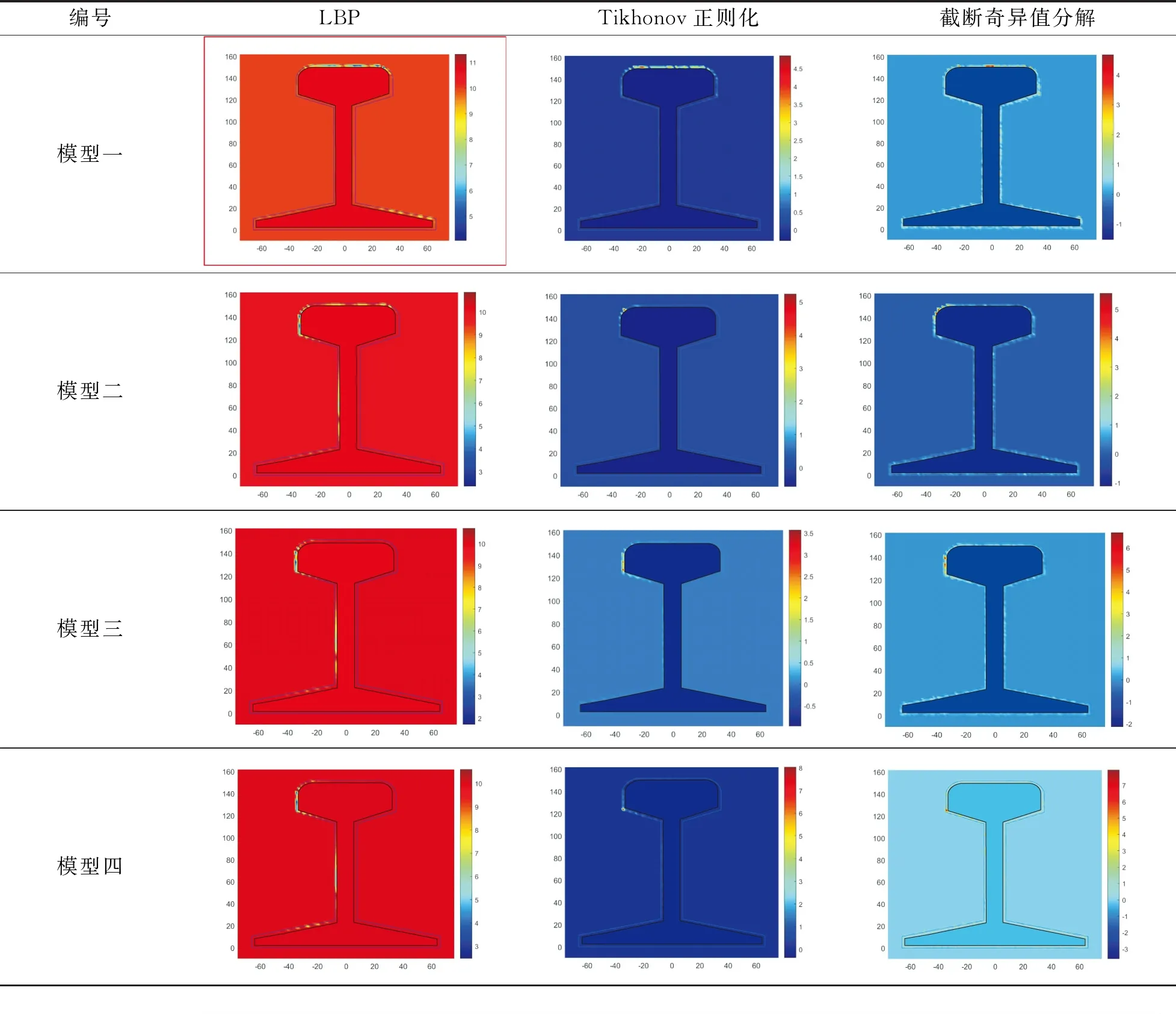
表1 九种损伤的图像重建结果
损伤重建的图像中,钢轨非浅表面区域采用纯色填充,损伤所在位置用区别于非浅表面区域的颜色代替。仿真软件中,浅表面区域被分为3 914个网格,计算重建图像的电导率偏差,并通过插值算法对该区域进行插值就可以获得较为平滑的二维彩图结果。由图像重建结果可以看出,被检测对象为完整钢轨时,基于电磁层析成像技术的钢轨损伤检测是完全可行的。重建结果的图像误差和图像相关系数如表2所示。

表2 重建图像的图像误差IE和相关系数CC
从图像误差和图像相关系数表格可以看出,在本文提出的钢轨探伤模型中,Tikhonov正则化算法对损伤的重建更贴合理论损伤分布。Tikhonov正则化算法在三种算法中最优,可以用该算法作为优化过程的验证算法,验证图像重建效果的好坏。因此后续过程以Tikhonov正则化算法重建的图像为指标,进行传感器参数优化。
4.2 单参数优化结果
单参数优化过程中采用的5种损伤模型的位置分布为图4中的模型一、模型三、模型五、模型七、模型九。
(1)线圈与钢轨表面间距改变时优化指标和重建结果如表3、表4所示。实验中5种不同间距的钢轨探伤模型均可以对损伤进行重建,但随着线圈与钢轨间距的增加,逆问题求解的误差增加,图像相关系数下降。
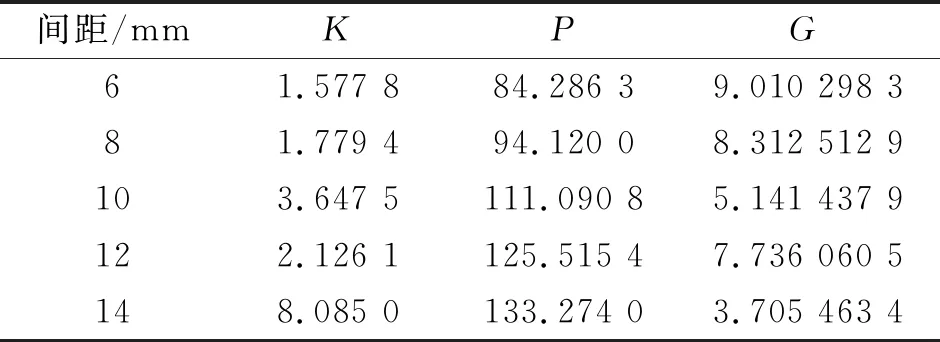
表3 线圈与钢轨表面间距变化的优化指标
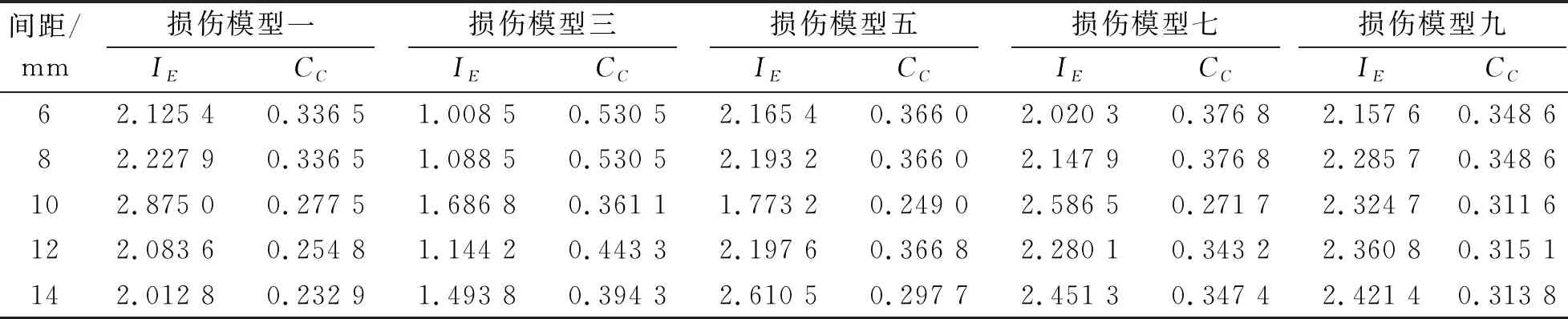
表4 表面间距变化重建图像的图像误差IE与相关系数CC
(2)线圈组间距改变时优化指标和重建结果如表5、表6所示。图像重建效果随线圈组间距改变的变化不大,主要影响灵敏度矩阵的均匀性,但随着线圈组间距的增加,图像重建效果略有下滑。
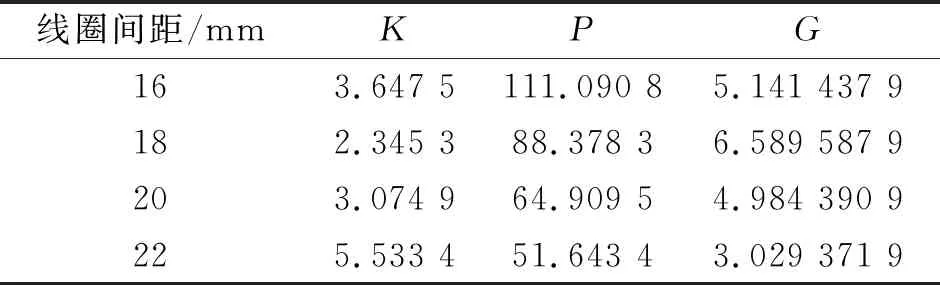
表5 线圈组间距变化优化指标

表6 线圈间距变化重建图像的图像误差IE与相关系数CC
(3)不同绕制方法下优化指标和重建结果如表7和表8所示。改变绕制方式主要影响灵敏度矩阵的条件数,对灵敏度矩阵均匀性影响较小,从而改变钢轨探伤系统的求解误差。

表7 不同绕制方法优化指标

表8 不同绕制方法重建图像的图像误差IE与相关系数CC
(4)不同匝数下优化指标和重建结果如表9、表10所示。改变绕制匝数主要影响灵敏度矩阵的均匀性,对灵敏度矩阵条件数影响较小,但综合来看,改变传感器线圈绕制匝数对图像重建性能影响不大。

表9 不同匝数优化指标

表10 不同匝数重建图像的图像误差IE与相关系数CC
在单参数优化过程共进行实验16组,分别包含了线圈组与钢轨间距、线圈组间距、线圈绕制方式、线圈匝数这四个参数的优化。将传感器设计参数和模型优化函数、图像重建结果进行联系。以RE作为图像重建性能的判定标准,RE定义如式(15),即对每类损伤计算CC/IE,然后平均5类损伤图像重建的CC/IE,作为RE的结果。5类损伤的模型优化函数G和图像重建结果RE如图5所示。
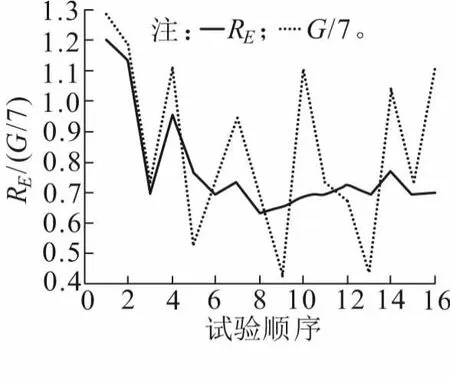
图5 图像重建效果与模型优化函数结果
由图5可以看出,模型优化函数与图像重建结果具有正相关性质,并且这一性质在误差允许范围内。当模型优化函数减小时,图像重建结果也会随之减小。因此可用模型优化函数间接表示图像重建结果的好坏,从而省去优化过程中图像重建结果的验证过程,验证了模型优化函数的合理性。
4.3 复合参数优化结果
单一参数优化过程说明减小线圈与钢轨间距、减小线圈组间距、减小线圈匝数、改变线圈的绕制方式都有助于优化传感器结构,从而提高钢轨探伤模型的图像重建效果,但这种方式并不是绝对的,需要复合参数优化过程的验证。
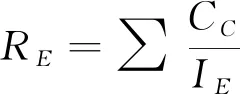
(15)
钢轨探伤模型的传感器复合参数优化过程是在一定约束下的优化,参数优化的约束条件是:①线圈间距大于线圈外径;②线圈外径大于线圈内径;③建模时线圈间不能交叉。
基于此约束,设置了复合参数优化过程各传感器设计参数的范围,具体如表11所示。比较特殊的传感器设计参数为线圈绕制方式,当线圈组间距为10 mm时,绕制方式只选择了内径为2 mm、外径为6 mm的绕制方式。当线圈组间距为12 mm时,选取了三种绕制方式:增加内径2 mm、外径8 mm,内径4 mm、外径8 mm。当线圈组间距为14 mm时,选取了4种绕制方式:内径2 mm、外径6 mm,内径2 mm、外径8 mm,内径4 mm、外径10 mm,内径6 mm、外径10 mm。当线圈组间距为16 mm时,选取了4种绕制方式:内径2 mm、外径6 mm,内径2 mm、外径10 mm,内径2 mm、外径12 mm,内径8 mm、外径12 mm。尽管线圈组间距不同时有的绕制方式少于4种,但可将绕制方式认为存在4种,例如线圈组间距10 mm时,4种绕制方式都为内径2 mm、外径6 mm,从而模拟正交实验法生成正交实验表。
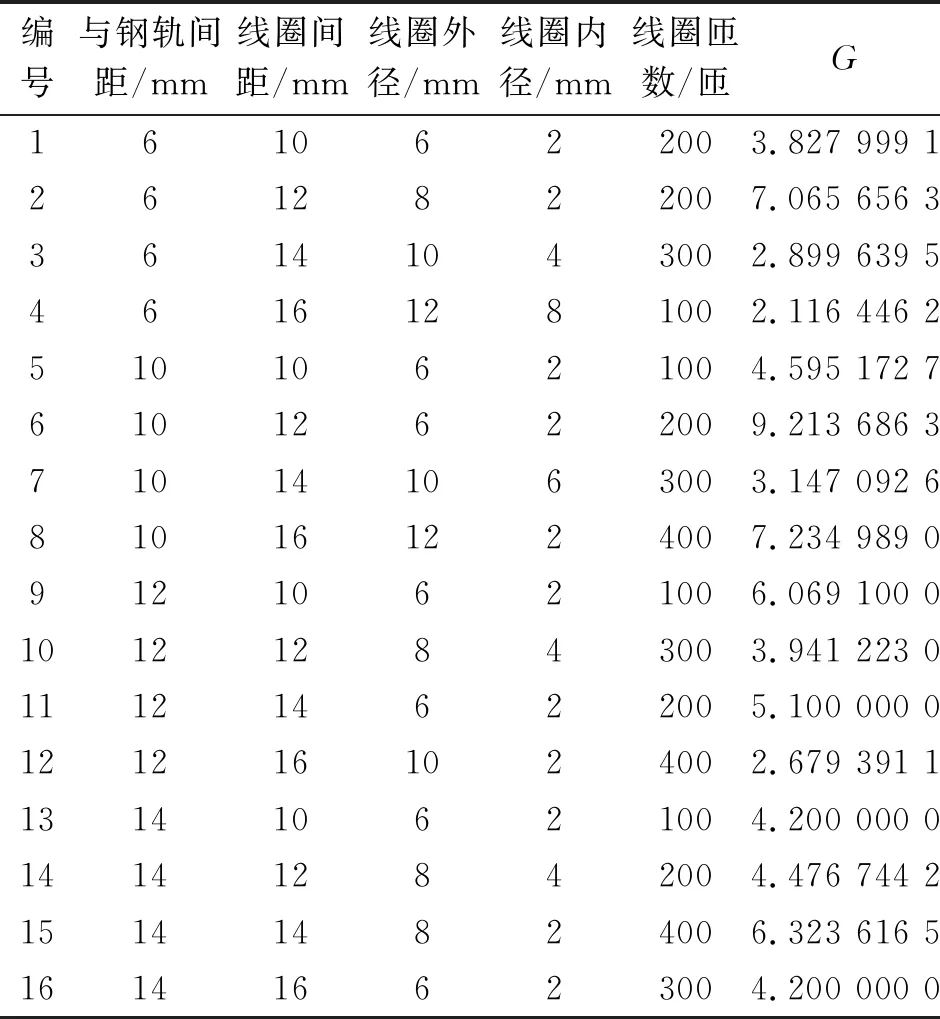
表11 模拟正交实验结果
以四因素四水平正交实验表为参考,做出模拟正交实验表格,正交实验结果如表11所示。
对模拟正交实验法进行极差分析,结果如表12所示。K1、K2、K3、K4为单一元素的四种水平,表中K1、K2、K3、K4所在行为对应因素的平均模型优化函数,R为对应因素取K1、K2、K3、K4时平均模型优化函数的极差,极差表反映该因素在选取不同水平时结果的差异,极差越大,说明该因素对钢轨探伤模型图像重建性能的影响越大。
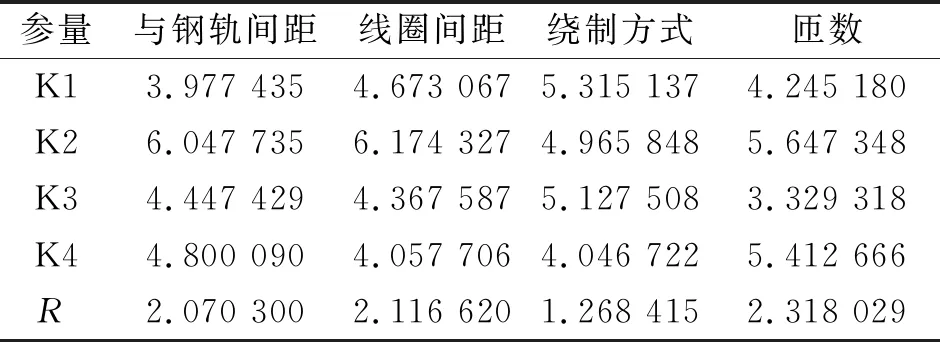
表12 因素极差与各水平优化函数
由表12可知,线圈匝数对模型优化函数G的影响最大,其次是线圈组间距、线圈组与钢轨表面的间距、线圈绕制方式。模型优化函数G值越大,模型图像重建效果越好,此时传感器参数的最佳组合为:线圈组与钢轨表面间距为10 mm,线圈组间距为12 mm,线圈绕制方式为线圈外径6 mm、内径2 mm,线圈匝数为200。此组数据正好在实验范围内,模型优化函数G为9.21,在实验范围内模型优化函数最大。
单个损伤存在是最基本、最普遍的情况,单损伤检测过程仍然以九种单损伤模型为基础,分析参数优化前后钢轨探伤模型的图像重建效果,重建后的图像对比结果如表13所示。

表13 重建图像的图像误差IE与相关系数CC
表中结果证明,经过参数优化后,钢轨探伤模型对损伤重建的效果明显优于未优化的钢轨探伤模型,证明了整个参数优化过程的正确性。
5 结束语
本文基于仿真实现了钢轨探伤传感器的设计与优化,实现了钢轨截面损伤的检测与定位。仿真结果证明将电磁层析成像应用于钢轨截面探伤是完全可行的,提出的模型优化函数与图像重建性能具有正相关特性,实现了灵敏度矩阵与图像重建性能函数关系的确定,提出的模型优化函数可以作为钢轨探伤模型优化的指标,反映钢轨探伤模型探伤性能的好坏,从而为传感器设计参数与探伤性能的连接做了铺垫。然而由于缺乏实测数据的支持,不能保证实际应用中损伤检测的效果,造成本文的实用意义有所减少。

