浅埋地铁车站结构变阻尼比反应谱影响因素
张亚辉,郭唯伟,徐 强,樊浩博
(1. 河北城乡建设学校, 石家庄 050043;2. 河北省电力勘测设计研究院, 石家庄 050031;3. 石家庄铁道大学 道路与铁道工程安全保障省部共建教育部重点实验室, 石家庄 050000;4. 石家庄铁道大学土木工程学院, 石家庄 050000)
0 引言
地震发生时,对建筑物或构筑物结构动力反应产生重要影响的因素为地震动的震幅、频谱和持时。振幅一般指地震加速度、速度或位移的峰值,由于加速度a的大小可以表示地震动的强弱,而且与质点运动的惯性力相联系,因此中国抗震规范均采用水平地震加速度作为衡量地震动振幅的指标。反应谱是在给定地震动作用期间,单质点体系的最大位移反应、最大加速度或最大加速度反应随质点自振周期变化的曲线。即同一阻尼比下,不同周期的场地在某地震波作用下的最大加速度反应、加速度反应谱与场地的类别息息相关。
其中,建筑物的阻尼性能对其振动反应有重要影响,阻尼比是反映结构阻尼性能的主要参数。GB50011—2010《建筑抗震设计规范》(2019 修订版)(以下简称现行规范)的地震作用计算中,考虑了阻尼比变化对反应谱曲线的影响。
随着中国经济的快速发展,越来越多的人开始研究阻尼对设计谱的影响。王亚勇等[1]研究了不同阻尼比情况下长周期段反应谱的特性,提出不同阻尼反应谱可以通过对阻尼比为5%的谱调整得到;张椿民[2]基于一维场地分析采用整体式反应位移法和等效线性化时程分析法对地下二、三、四层地铁车站进行了结构抗震分析,结果表明:通过一维场地分析方法确定的土层参数以及基岩波能够满足整体式反应位移法和等效线性化时程分析法的输入条件;李春锋等[3]对台湾集集地震的长周期地震动特性进行研究的结果表明,反应谱的形状主要受场地条件和震级控制,受距离的影响并不显著,近断层长周期地震动明显受断层活动特性影响,上盘的长周期地震动比下盘的强。
1 单向水平地震波反应谱分析模型
为详细研究不同阻尼比条件对结构的地震动力反应的影响,选取北京地铁单层双跨车站为研究对象,运用结构分析软件对车站主体结构的水平单向地震动力反应进行数值模拟分析,结构动力特性参数见表1。车站埋深4.8 m,模型计算范围水平方向取为85 m(5 倍地铁车站宽度)[4-7],竖向从地表取至22.2 m 深度处更新世砂土层,车站的结构截面如图1 所示。

图1 单层双跨车站横断面图(单位:mm)Fig. 1 Cross-sectional view of single-storey double-span station (mm)

表1 分析结构的动力特性参数Table 1 Analysis of dynamic characteristic parameters of structures
计算模型网格化分如图2 所示,北京地区各土层参数见表2,单元力学参数见表3 所示。

图2 土-结构模型网格化分图Fig. 2 Meshing of soil-structure model
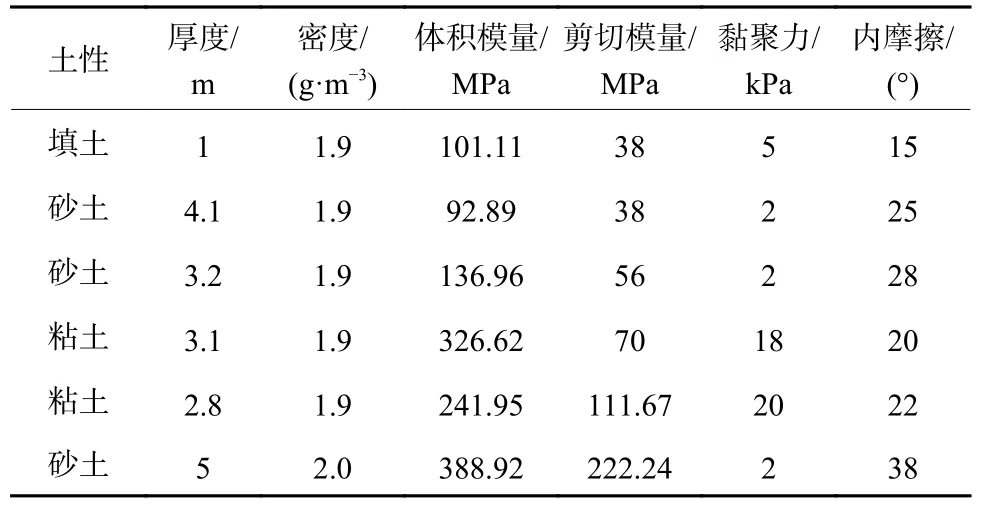
表2 北京地区场地土模型物理力学参数Table 2 Physical and mechanical parameters of site soil model in Beijing area

表3 接触单元力学参数Table 3 Mechanical parameters of contact elements
基岩地震波采用经过基线矫正的表4 中列举的8 条地震波。地震波信息如表4 所示。
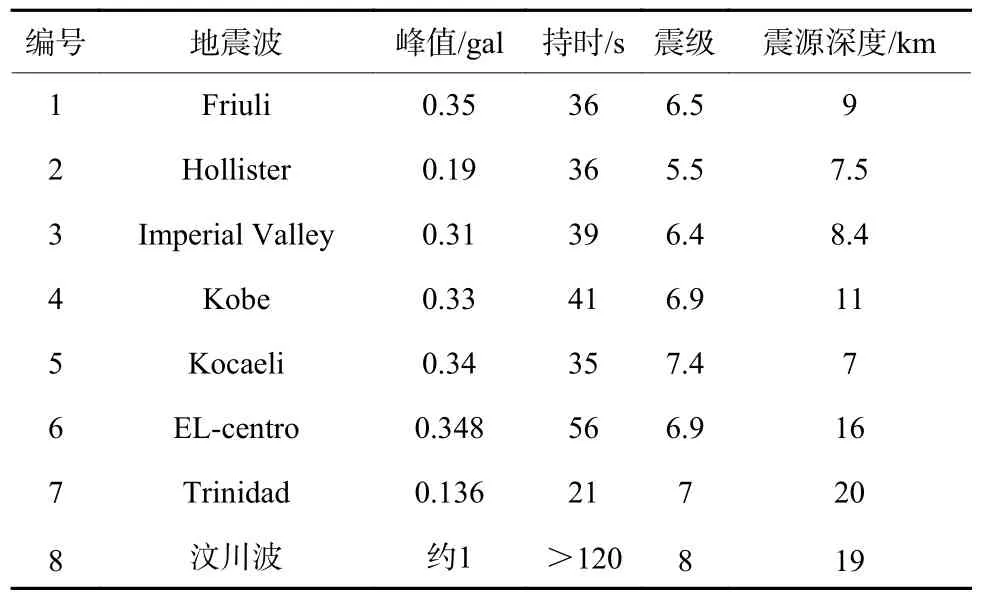
表4 选取地震波记录信息汇总Table 4 Select seismic wave record information summary
2 框架地铁地震波反应谱分析
2.1 变阻尼比条件下地震波反应谱分析
针对反应谱中阻尼理论研究的不足,考虑变阻尼比对反应谱的影响,建立基于阻尼影响系数研究变阻尼比条件下的反应谱。
根据文献[8-9]中提出的基于结构竖向广义相对剪切变形γ,针对不同结构形式的变阻尼比作为图-结构相互作用体系中结构阻尼比ξ。对于钢筋混凝土框架结构其公式为:
式中:γ为相对剪切变形。γ的取值如表5 所示,从而可以得到如图3 所示的在变阻尼比条件下的各地震波对应的β谱以及平均化后的β谱(图中的黑实线代表平均谱线,灰线表示各地震波对应的反应谱)。
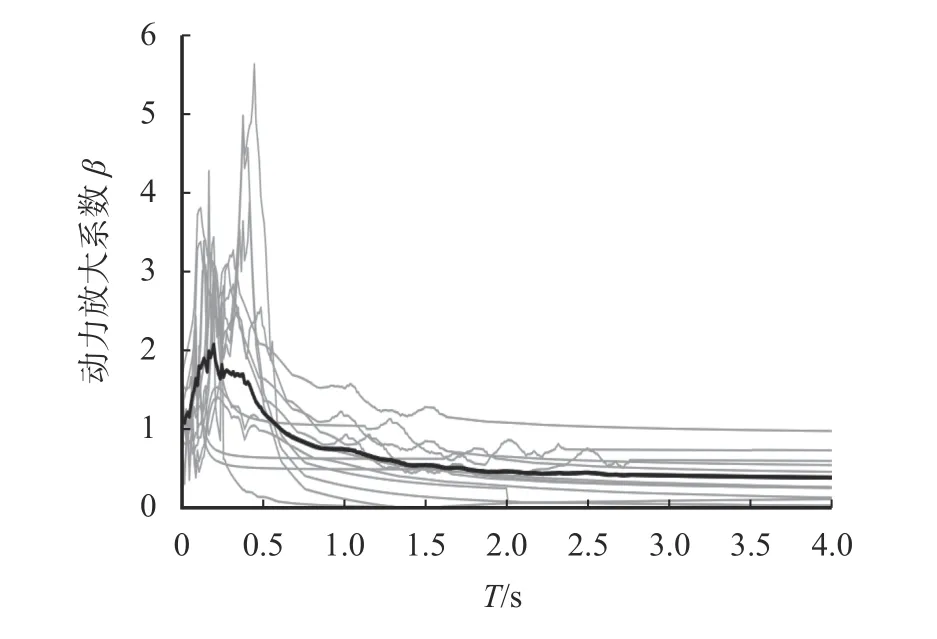
图3 变阻尼比条件下平均化β 谱Fig. 3 Averaged β spectrum of variable damping ratio
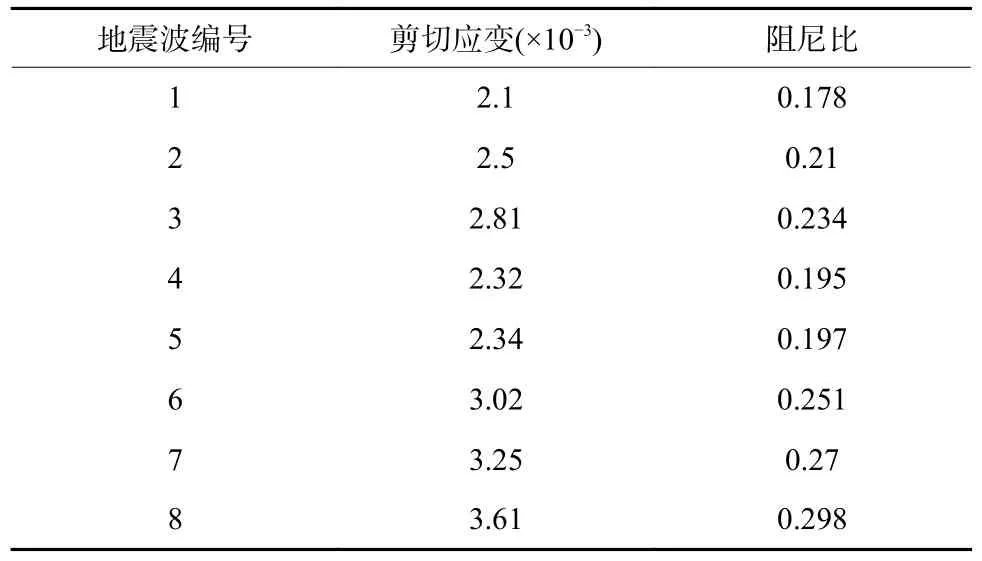
表5 结构相对剪切变形与阻尼比对照表Table 5 Comparison table of relative shear deformation and damping ratio of structures
由图3 可以看出:变阻尼反应谱的变化规律与常阻尼比条件下的谱线变化规律相近,即每条谱线也均可大致分为4 个阶段:上升段、波动段、下降段以及水平段。
2.2 反应谱的阻尼修正
以阻尼比为5%时的反应谱曲线为准,其他阻尼比条件下的反应谱均以此为基础进行修正[10-11]。其中,非线性阻尼反应谱修正系数为:
图4 为8 度设防条件下,单层双跨地铁车站结构的变阻尼比修正系数曲线。图中细实线为每一条地震波作用时得到的变阻尼比修正系数曲线,粗实线为平均化的修正系数曲线。
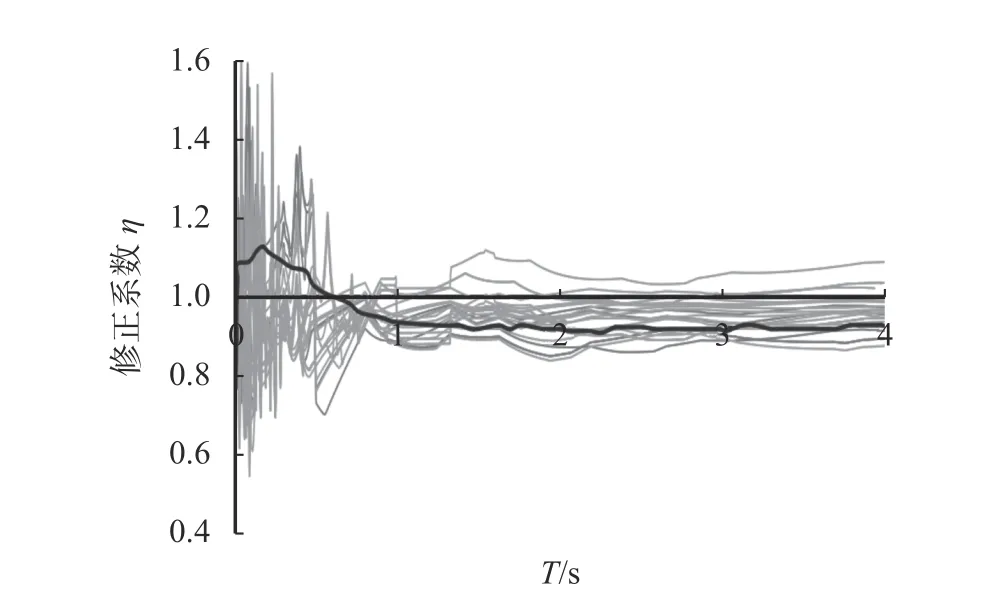
图4 地铁车站的变阻尼修正系数曲线Fig. 4 Variable damping correction coefficient curve of subway station
从图4 中可以看出:当结构自振周期在0.5 s 之内时,车站结构的阻尼修正系数η大于1。随着结构自振周期延长,其修正系数曲线逐渐小于1,并且趋于一个稳定值。
对8 条地震波进行峰值修正,故按照上述与8 度设防时计算阻尼修正系数同样的步骤对6、7、9 度设防分别绘出η曲线(图5)。
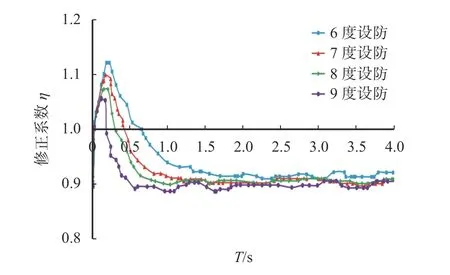
图5 各设防烈度下变阻尼比修正系数曲线Fig. 5 Correction coefficient curves of variable damping ratio under different fortification intensities
由图5 可以看出阻尼修正系数曲线的特点:在0.2 s 之前,呈直线上升趋势,随着设防烈度的增大,直线斜率有所减小,但仍为正值;0.2 s 之后,曲线呈指数式减小,直至稳定,其稳定值为0.90~0.92,随设防烈度改变而有微小的变化。
将设防烈度和自振周期作为2 个自变量建立函数,其中自振周期T为主控变量,对该修正系数进行拟合。
为便于应用,对图5 中各条修正系数曲线进行回归拟合计算。根据以上修正曲线的函数特点可以得到地铁车站结构阻尼修正系数的拟合式:
式中:T为结构自振周期;L为设防烈度;q为设防烈度影响系数,按照表6 取值。

表6 设防烈度影响系数q 的取值Table 6 Value of the impact coefficient q of fortification intensity
图6 为不同设防烈度下,根据上式绘制的修正系数曲线的拟合值与实际值的比较。图中黑实线为各级设防烈度下的修正系数拟合曲线,虚线代表对应的实际曲线。
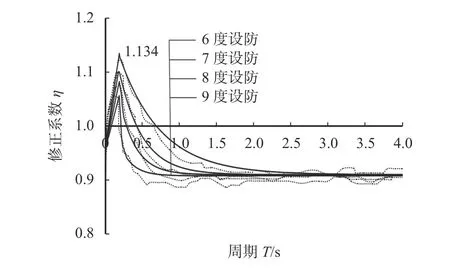
图6 变阻尼修正系数拟合曲线Fig. 6 Fitting curve of variable damping correction coefficient
图6 可看出,拟合曲线能够很好地反映修正系数平均曲线变化趋势。
3 建立变阻尼比地震影响系数曲线
根据《建筑抗震设计规范》(GB50011—2010)的规定,可以用α表示地震系数k和动力系数 β的乘积,并将该结果称为地震影响系数即:.
根据图3 得到的7 度设防条件下的β谱和设防烈度下对应的地震系数k,可以得到对应的一条水平地震影响系数α曲线(图7)。
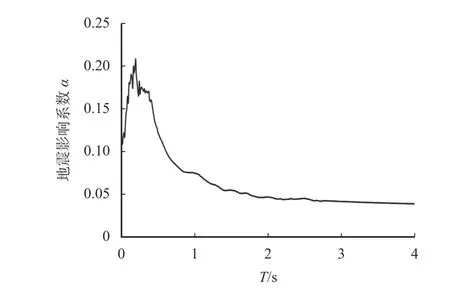
图7 8 度设防水平地震影响系数曲线Fig. 7 Seismic influence coefficient curve at 8 degrees fortification level
将图7 的水平地震影响系数曲线进行标准化处理,即将地震影响系数曲线变为标准化的平滑曲线,标准化后的影响系数曲线消除了在不同地震动强度下的差异性变化(图8)。
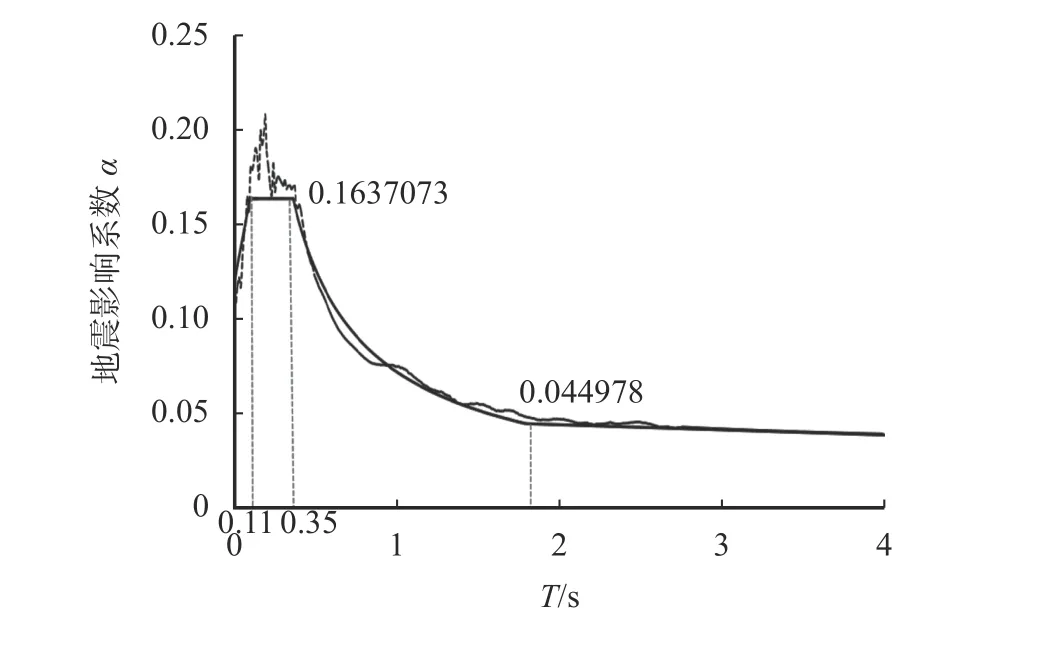
图8 8 度设防水平地震影响系数规准曲线Fig. 8 Seismic influence coefficient calibration curve at 8 degrees fortification level
4 变阻尼比反应谱特性分析
影响地铁车站的地震响应有许多因素,如地震设防烈度、地震波的峰值和频率特性、场地条件以及结构埋深等。
4.1 地震设防烈度的影响
图9 为不同设防烈度下的变阻尼比相对反应谱曲线。
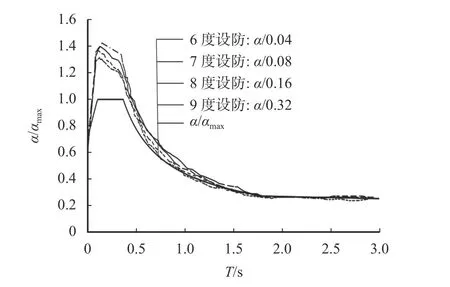
图9 不同设防烈度下的相对反应谱曲线Fig. 9 Relative response spectrum curves of different fortification intensities
从图9 可以看出,不同设防烈度下的非线性阻尼比设计反应谱具有不同的形状,设防烈度越高,规准化反应谱越低,这与实际地下建筑结构的非线性阻尼机理相一致。由于此时结构变形较大,结构平均阻尼比超过5%,导致地铁车站结构规准化反应谱曲线中长周期部分在规准化标准反应谱线下方。
4.2 围岩参数的影响
围岩参数中影响反应谱(地震影响系数)的主要因素有:内摩擦角和黏聚力。由于现在既有明挖地铁车站多修建于浅埋土质围岩中,岩石围岩明挖车站比较少见。因此,主要针对Ⅴ、Ⅵ级围岩,不断改变内摩擦角和黏聚力得到不同参数条件下的反应谱,从而定量地给出两参数与地震影响系数的关系。基本围岩参数表如表7 所示。
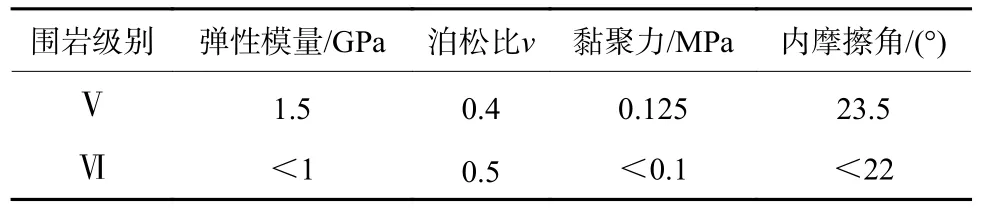
表7 围岩材料力学参数Table 7 Mechanical parameters of surrounding rock materials
根据表7 参数,运用控制变量法分别改变黏聚力、摩擦角以及泊松比,得到不同泊松比、黏聚力以及内摩擦角影响系数曲线(图10~12)。
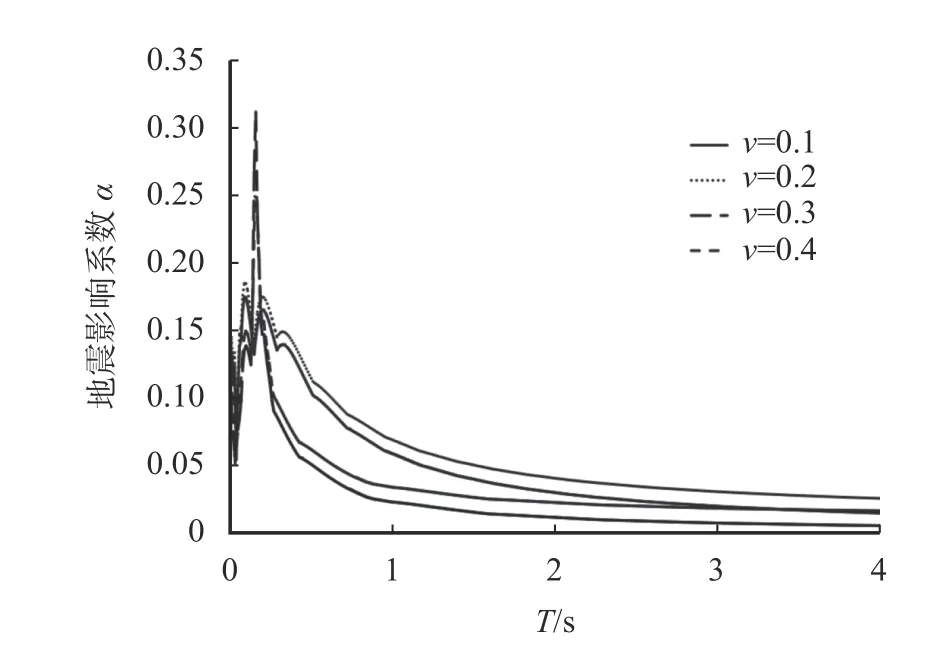
图10 不同泊松比影响系数曲线Fig. 10 Influence coefficient curves of different
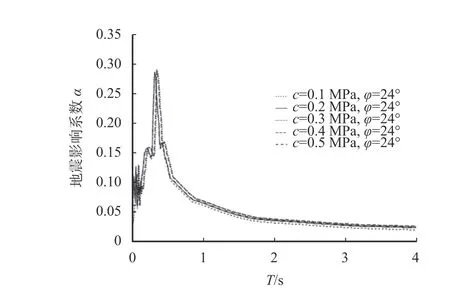
图11 不同黏聚力影响系数曲线Fig. 11 Influence coefficient curves of different cohesion
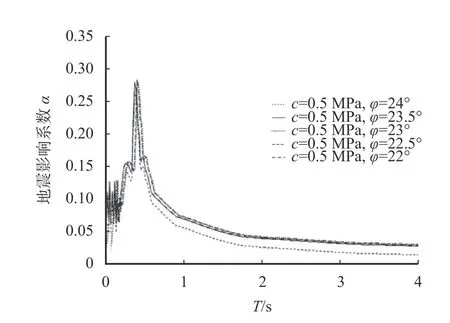
图12 不同内摩擦角影响系数曲线Fig. 12 Influence coefficient curves of different internal friction
由图10~12 可知,黏聚力与内摩擦角的变化几乎没有引起反应谱的变化,只是在小范围内峰值发生了移动,移动量在0.01 s 范围内;而当泊松比发生变化时,地震影响系数峰值及形状都发生了改变,峰值随泊松比的增大而增大,这就意味着围岩逐渐变弱时,地震对结构的影响在增大,地震影响系数当然要随之增大,但影响在数值和公式上的表示,还需要进一步探讨。
用同样的方法,使泊松比改变幅值尽量的小,每0.1 划分为10 份即增加幅值为0.01,定量地找出泊松比与地震影响系数峰值之间的对应关系。表8为由于泊松比的改变引起的地震影响系数峰值改变的规律。
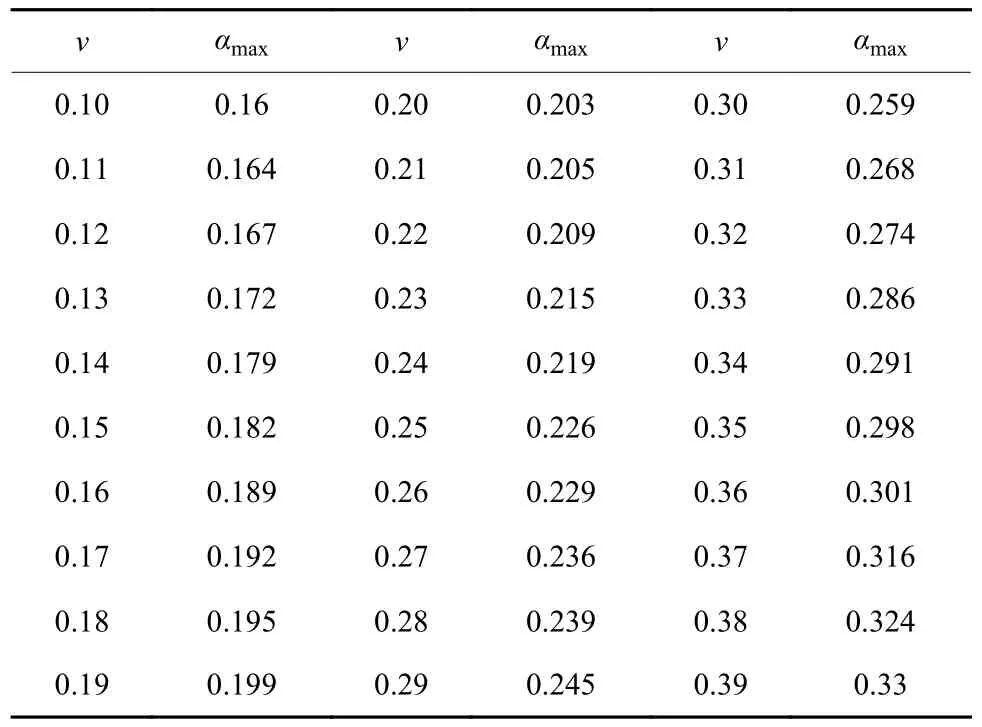
表8 泊松比与地震影响系数峰值关系Table 8 Relationship between Poisson's ratio and peak value of seismic impact coefficient
4.3 地下车站结构埋深的影响
对埋深为2 m、5 m、10 m、15 m、20 m 和25 m六种工况进行计算,进行平均规准化后得到各结果(图13)。
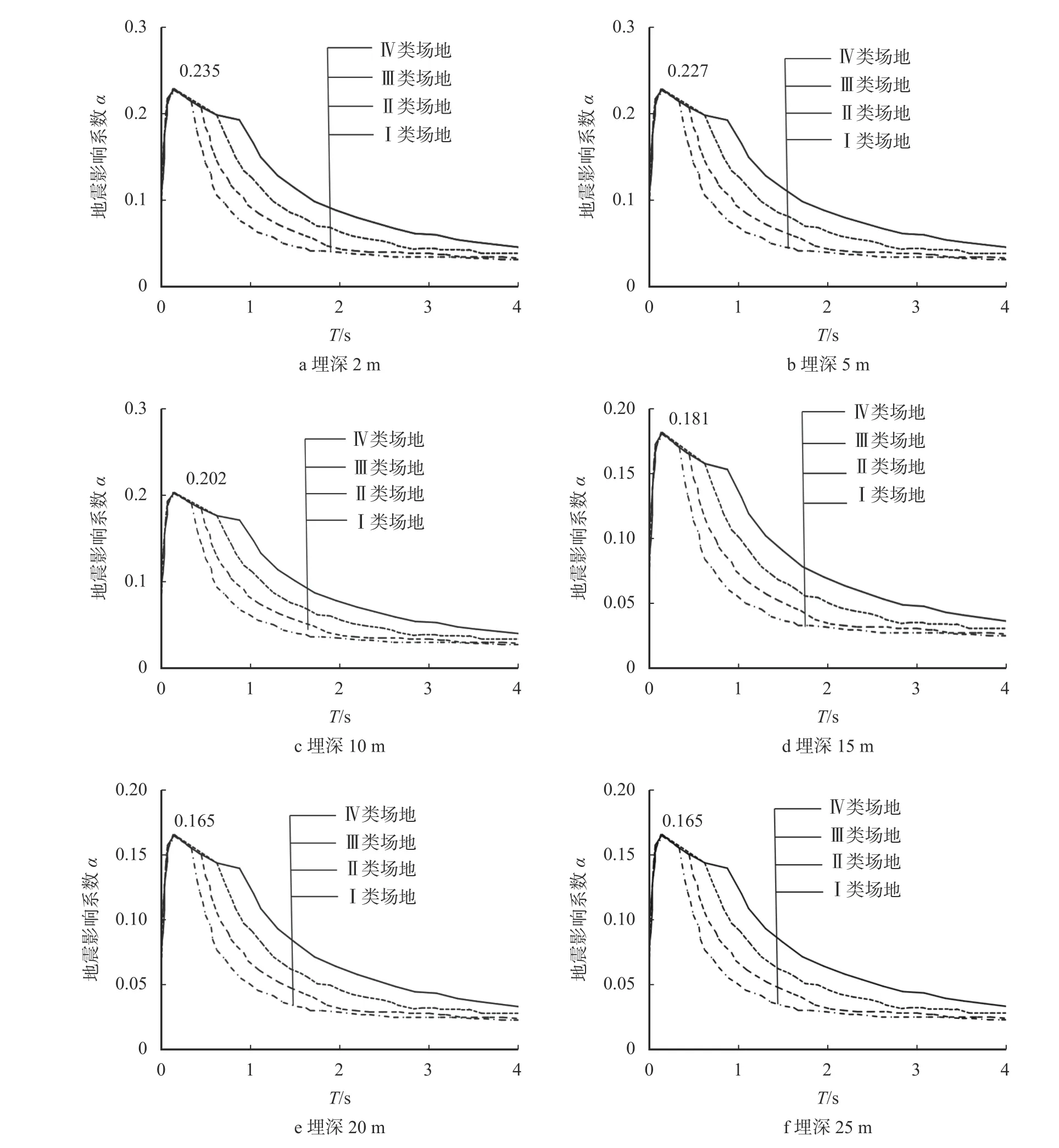
图13 埋深对非线性阻尼比反应谱的影响Fig. 13 Effect of burial depth on nonlinear damping ratio response spectrum
由图13 可以看出:随着埋深的增加,各类场地土的影响系数峰值逐渐减小。这是由于埋深的增大,在一种波的作用下有更多的土体对地震波起到了滤波作用,使得地震波加速度逐渐得到衰减,对地下结构的动力反应而言即逐渐减小;在埋深为2 m时更接近规准化设计反应谱的峰值,值为0.229。
5 结论
通过对单层双跨结构地铁车站进行动力数值模拟分析,研究各种因素下变阻尼比对反应谱的影响规律,并且在变阻尼比条件下对阻尼修正系数进行研究,得到如下结论。
1)不同设防烈度下的变阻尼比设计反应谱具有不同的形状,设防烈度越高,规准化反应谱越低,这与实际地下建筑结构的变阻尼机理相一致。
2)围岩参数中,黏聚力与内摩擦角的变化对结构的地震影响系数的影响较小,即只在小范围内峰值发生了移动;而当泊松比发生变化时,地震影响系数峰值及形状均明显发生了改变,峰值从泊松比为0.2 时的0.17 增加到了泊松比为0.4 时的0.32,增大幅值近一倍。这就意味着围岩逐渐变弱时,地震对结构的影响在增大,地震影响系数当然要随之增大,
3)随着埋深的增加,在地震波的作用下,土体的滤波作用愈加明显,该作用加速了地震波能量的衰减,进而造成地下结构的动力反应程度较弱。当框架结构车站的埋深为2 m 时,框架结构的反应谱峰值更接近规准化设计反应谱的峰值,值为0.229。

