《借根方比例》中开方算法之来源新探
贾洪岩 纪志刚
(1.中共上海市闵行区委党校,上海201199; 2.上海交通大学科学史与科学文化研究院,上海200240)
康熙年间,《借根方算法》(1700,以下简称“《算法》”)首次通过西方代数学传入中国,作者是比利时传教士安多(Antoine Thomas,1644—1709)[1],书中介绍了西方的开方算法①本文将解未知数的计算方法,如(xn=a)、(axn±bxm=c),统称为开方算法。 称xn=a 的解法为高次幂开方算法,其中解2 次幂的方法为开平方法,解3 次幂的方法为开立方法,解其余次幂的方法为n 次幂开方算法(n≥4)。称axn±bxm=c 的解法为高次幂方程解法,其中解2 次幂的方法为二次幂方程解法(或带纵平方法),解3 次幂的方法为三次幂方程解法(或带纵立方法),解其余次幂的方法为n 次幂方程解法(4≤n≤6)。。 1712 年,康熙开蒙养斋,梅瑴成(1681—1763)、何国宗(? —1767)等人应召入馆并编撰《数理精蕴》,《数理精蕴》下编卷31—36《借根方比例》(以下简称“《比例》”)即以《算法》为底本改编而成。
《比例》卷32、33 分别介绍了高次幂开方算法(xn=a)和高次幂方程解法(axn±bxm=c),在清初算家看来“借根方比例法中,开各乘方为最要”([2],下编卷32 页2)。 也许因为“宋元时期的增乘开方法失传之后,这是第一次给出高次方程的数值解法”[3],所以《比例》卷33 中的高次幂方程解法也一直备受当代学者的关注。 通过对卷33 中三次幂方程解法的分析,先前研究一般认为卷33 中的高次幂方程解法来源是中、西双方二者之一①李俨、韩琦认为此法即西方的“牛顿法”,魏保华、潘亦宁也支持西方来源的观点。 钱宝琮、李迪虽然承认三次幂方程解法与“牛顿法”完全相同,但《数理精蕴》是否受到影响需进一步研究。 李兆华则认为三次幂方程解法“是由中国古代的开带纵立方法,即《数理精蕴》卷24 的方法,演变来的”。 参见参考文献[3—10]。。
但是,关于《比例》卷32 中高次幂开方算法(xn=a)的来源②魏雪刚指出《比例》卷32 中的高次幂开方算法与《少广拾遗》的开方算法一致,指出了两书之关联,但称两书中的开方算法一致似有不妥(参见参考文献[11])。 实际上《比例》只是吸收了《少广拾遗》的部分内容,并非一致,具体分析见下文。,《比例》卷33 中的4—6 次幂方程解法(axn±bxm=c)的来源,以及卷32、33 中开方算法之关系的研究有待加强,而这些算法实际上有非常紧密的关系,应放在一起讨论,方可探明原委。 因此,《比例》中的高次幂开方算法与高次幂方程解法有怎样的关系? 不同次幂的解法有何异同? 它们又是从何而来? 本文基于“古证复原”原则,对比分析了与《算法》《比例》密切相关的几部算书,为《比例》中的高次幂开方算法、高次幂方程解法之来源给出一种新的可能。
1 相关算书开方算法之异同
1.1 《算法》与《比例》简要对比
虽然《算法》是《比例》的底本,但两书中大部分的开方算法并不相同。 总的来说,两书中开方算法的异同关系如图1 所示。
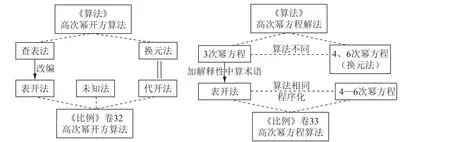
图1 《算法》《比例》部分开方算法对比
《算法》介绍了4—9 次幂的开方算法(xn=a),以及2、3、4、6 次幂的方程解法(axn±bxm=c)。 书中都是尽可能使用“换元法”进行计算,比如,将x4=a 视为X2=a(X=x2);将x6=ax3+b 视为X2=aX+b(X=x3)。 只有在无法使用此法时,安多才给出特殊的计算方法,即5、7 次幂开方算法(即x5=a、x7=a,以下简称“查表法”)和三次幂方程解法(即ax3±bx2=c),它们与中算传统不同,是纯粹的数值运算,安多也没有对这些运算过程作任何解释说明。
《比例》卷32 介绍了高次幂开方算法(xn=a)(3—10 次幂),清初算家为不同次幂给出了三种开方算法,与本卷开始处介绍的顺序一致,分别为“未知法”③由于此算法在处理3—10 次幂时具备机械化、程序化的特征,拥有相同的算法原理,且此算法的来源未知,故而将这种计算方法称作“未知法”,此名称为笔者命名,并非出自《比例》原文。、“代开法”“表开法”。 基于开篇以及之后案例中的介绍逻辑,可知三种计算方法虽然不同,但应该是并列关系。 在“未知法”之后,“代开法”之前,还有“盖几乘方之本法,有……”字样,之后的内容是对“未知法”中部分步骤的猜测性解读(分析见下文)。
在这三种开方算法中,“代开法”和《算法》的“换元法”相同,“表开法”改编自《算法》的“查表法”①“表开法”与“查表法”的算法流程基本相同。 由于清初算家清楚“查表法”的算法原理,所以将《算法》中仅有的5、7 次幂“查表法”作了改进和拓展,使其能够适用于3—10 次幂,并为它们配备了“新数表”。,二者的来源比较清晰,因此本文不对它们做具体分析。 本文主要讨论的一个问题,即卷32 中“未知法”的来源和构造过程②关于清初算家构造“未知法”与“表开法”的先后问题,尚未有证据明确指出二者的先后顺序,笔者认为二者应该是同时构造的。 但如果一定要区分构造它们的先后顺序,笔者以为,应该是先有“未知法”,后有“表开法”。 原因在于,“表开法”中所需要的数值,“未知法”里都有,且明确了数值的计算方法。 但是,“未知法”所需要的整个运算流程,“表开法”是没有的。(下文关于卷32 中高次幂开方算法的讨论均指“未知法”,特此说明)。
《比例》卷33 介绍了高次幂方程解法(axn±bxm=c)(3—6 次幂)。 其中,三次幂方程解法倍受关注,正是基于对它的分析,前人学者才得出了《比例》中高次幂方程解法的来源是中、西双方二者之一的结论。 但是,《比例》卷33 中不只有三次幂方程解法,还有4—6 次幂方程解法,且4—6 次幂方程解法的来源未知,同时,卷33 中的3—6 次幂方程解法还呈现出了统一的、机械化、程序化特征。 因此,本文的另一个主题是将《比例》卷33 中的3—6 次幂方程解法视为一个整体,来探讨其来源和构造过程,而不只是针对其中的三次幂方程解法。
综上,首先,目前已知《比例》卷32 中的“代开法”“表开法”源自《算法》,但“未知法”的来源有待探究。 其次,《比例》卷33 中的三次幂方程解法源自《算法》,但4—6 次幂来源未知。 因此,为了更好地探究卷32 中的“未知法”以及卷33 中的高次幂方程解法的来源,有必要对与《比例》《算法》有紧密关系的其他算书作对比分析,为溯源工作打好基础。
首先,安多在编撰《算法》时引用了《算法纂要总纲》(以下简称“《总纲》”),此书同样为安多所作,约成书于1689—1695 年间[12],因而不能忽略此书。 书中介绍了平方、立方、带纵平方、带纵立方四种开方算法。 其次,《比例》作为《数理精蕴》的一部分,《数理精蕴》卷11、23、24 中的开方算法也应得到关注。 其中,下编卷11 介绍了平方、带纵平方算法,卷23、24 介绍了立方、带纵立方算法。 再次,在《数理精蕴》的编撰者中,梅瑴成自幼受梅文鼎的影响,何国宗及分校官魏廷珍、王兰生也都曾和梅文鼎学习过数学和天文[3],加上《比例》卷32 中有部分内容与《少广拾遗》中的计算方法十分相似,因此,梅文鼎的《少广拾遗》也值得我们留意。 书中介绍了“诸乘方大法”,可以处理3—13 次幂的开方算法(xn=a),但此法的算法流程和算法原理与“未知法”并不相同。
1.2 相关算书之对比
由于《总纲》《数理精蕴》(卷11、卷23、卷24)均不涉及3 次幂以上的开方算法,因此,在此处先探讨《比例》卷32 中“未知法”的开平方、开立方法,以及《比例》卷33 中二次幂、三次幂方程解法与《总纲》《数理精蕴》之关系。
首先,关于《比例》卷32“未知法”的开平方、开立方算法(关系参见图2)。 对比《总纲》《比例》《数理精蕴》(卷11、卷23)可知:其一,《数理精蕴》卷11、23 中的开平方、开立方算法属于清初算家所谓的“常法”,算理与《九章算术》无异。 其二,《比例》“未知法”中的开平方、开立方算法都异于“常法”,与中算传统开方法迥异。 其三,《总纲》的开平方法与“常法”相同,与《数理精蕴》卷11 的步算过程相同;开立方法则异于“常法”,与《比例》“未知法”的步算过程相同。

图2 《总纲》与《数理精蕴》《比例》中开平方、开立方算法之关系
其次,关于《比例》卷33 中的二次幂、三次幂方程解法(即开带纵平方、开带纵立方)。对比《算法》《总纲》《比例》《数理精蕴》(卷11、卷24)可知,几本算书中的带纵平方法(二次幂方程)大都相同,且与《算法统宗》的“归除平方带纵歌”类似[13],在此不作赘述。 关于开带纵立方(三次幂方程)算法(关系参见图3),《数理精蕴》卷24 属于清初算家所谓的“常法”,与《比例》大体相同但细节有异。 《算法》与《总纲》的表述形式、运算思路极为相近,安多曾在《算法》中称“此法与《总纲》内第十二节内带一纵开立方之法同”([14],页187),也许正因如此,才有学者认为二者是相同的[8],但如果回归文本内容仔细对比二者的算法过程可知,它们其实还是略有差别的①在求初商积时,《算法》是以多项式为基础,将初商带入x3+ax2,《总纲》则是将初商带入x2(x+a),二者的区别在于前者为数值运算,后者结合了立体几何图形的构造进行运算。 参见参考文献[15]。。 然而,虽然安多在《算法》中声称此法与《总纲》相同,但《比例》卷33 的带纵立方解法却沿用了《算法》的计算方法,而非《总纲》之法。 值得反思的是,《算法》和《总纲》的运算过程略有不同,但为何安多称二者相同②依笔者浅见,安多基于西方数学知识背景看待这两种算法,二者均为纯数值运算,因此认为二者算理相同。? 清初算家又为何使用了《算法》的方法,而没有使用《总纲》的方法? (分析见下文)
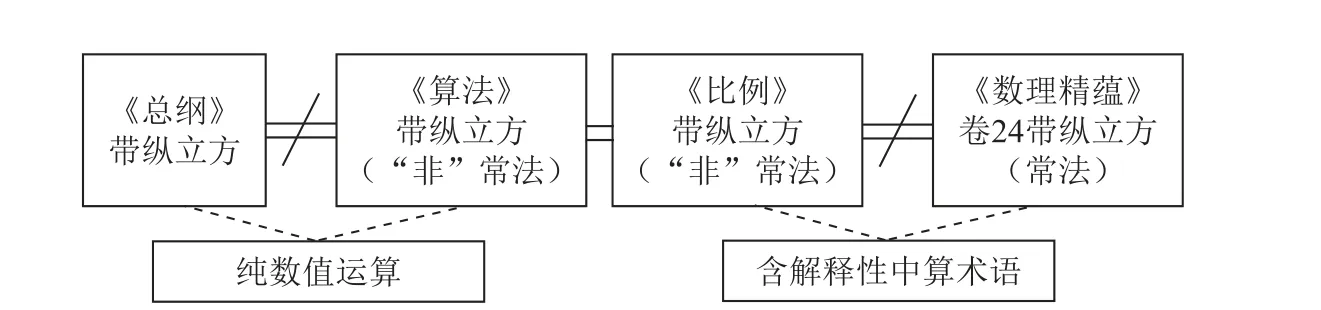
图3 相关算书中三次幂方程解法之关系
通过对比分析《算法》《总纲》《数理精蕴》和《比例》中的部分开方算法可知:首先,《比例》中的开方算法,除了二次幂方程解法,其余大都异于中算传统中的“常法”。 其次,《比例》卷32 中“未知法”的开立方法源自《总纲》,《比例》卷33 中的三次幂方程解法源自《算法》(图4)。 不同之处在于,《算法》《总纲》中的开方算法均属于纯数值运算,传教士安多并未对算法流程作任何解释,清初算家则是在《比例》中使用中算术语对相关算法作了解释说明。 但是,“未知法”的4—10 次幂开方算法、《比例》卷33 的4—6 次幂的方程解法来源仍是未知的,因此,下文将用两节分别讨论它们的来源。

图4 《比例》卷32、33 中部分开方算法来源
2 《比例》卷32“未知法”对《算法》《少广拾遗》的借鉴与会通
由于《比例》卷33 中的高次幂方程解法与《比例》卷32 中的“未知法”紧密相关,因而在本小节先探讨《比例》卷32 中“未知法”(3—10 次幂)的来源。 此外,虽然已知《比例》卷32 中的“表开法”改编自《算法》的“查表法”,且“查表法”与“未知法”的算法原理不同,但“未知法”却借鉴了“查表法”中的部分计算方法,因此,在探究“未知法”来源之前,需要对“查表法”作一简要介绍,为之后的探源工作做好铺垫。
“查表法”是通过查找“数表”中的两个数值(即“相近小数”与“次行之数”)来求得初商、次商和三商的,这两个数值与本文主题即《比例》卷32“未知法”、卷33 高次幂方程解法的由来密切相关。
以5 次幂“查表法”求解为例(x5=13383270465632)([14],页19),首先,要在“数表”中找到与被开方数13383270465632 前部分相近的“相近小数”,即130691232,通过此数值便可得到被开方数的初商(4)和次商(2)。 然后,再找到“相近小数”相同格内的“次行之数”,即15558480,用它便可得到三商的值。 7 次幂的步算过程也是如此,只是“数表”的数值不同,整个步算流程极为便捷。 实际上,清初算家正是参考了“相近小数”和“次行之数”这两个数值,才能将源自《总纲》的三次幂开方算法扩展至更高次幂,具体分析见下文。
2.1 “未知法”对“相近小数”之参考
基于上文分析可知,《比例》“未知法”的三次幂开方算法源自《总纲》,异于中算传统中的“常法”(如《数理精蕴》卷23)。 分析“未知法”与“常法”的区别,有助于进一步理解清初算家构造“未知法”时的思考方式,并探究这种计算方法的由来。
“未知法”和“常法”的算法流程都可以总结为以下10 个步骤:①定位;②定初商;③求初商积;④求次商廉隅之共积;⑤求次商廉法;⑥定次商;⑦求初商、次商共积;⑧求三商廉隅之共积;⑨求三商廉法;⑩定三商。 但是,二者的具体计算过程仍有不同,主要体现在步骤5、7、9 上(步骤5、9 的算法原理相同,因此可视为同一问题)。
清初算家曾在《比例》卷32 开平方法的末尾处直言,“此法止用廉法除余积,得次商,即并初商数自乘,得数復与原积相减,与常法不同”([2],下编卷32 页4)。 此段文字可以看做是对上述步骤5—8 的“解释说明”,对应了“未知法”与“常法”的不同之处,比如,“即并初商数自乘”对应“未知法”的步骤7(求初商次商共积),但是,这种异于“常法”的计算方法是怎么来的呢?
《数理精蕴》卷23 展现的“常法”计算思路符合中算传统“析理以辞,解体用图”这一特征,它将立方体“递析开之”,分为“方、廉、隅”几个立方体,分别计算它们的表面积和体积,以此逐步求次商、三商。 因此,在求初商、次商之共积时便需要使用“方、廉、隅”的相关数值反推求之,相应的,此法所需的计算量也比较大。 反之,《总纲》和《比例》“未知法”的三次幂开方算法在此步骤则节省了大量计算,它们只需“合并初商、次商,自乘、再乘”(初商+次商)3即可。
然而,这种“初商次商共积”的计算方法不只是出现在《总纲》的三次幂开方算法中,它同样出现在《算法》的“查表法”中。 如上文所述,5 次幂“查表法”是用“相近小数”130691232 求得初商、次商为4、2,而此数值130691232 正是“初商、次商相并再自乘四次”之结果(425),二者互为逆运算,同样的情况在7 次幂的“查表法”中同样存在。 由于这种逆向思维并不困难,所以清初算家完全能够意识到“数表”“中每格所列细数二层……上层为初商、次商积”([2],下编卷32 页44),即(初商+次商)n。
正所谓孤证不立,如果清初算家仅知道《总纲》中的这种计算方法,而没有见过“查表法”对“相近小数”的使用,其实很难保证他们能够将《总纲》中的这种异于“常法”的、仅出现在三次幂开方算法中的计算方法适用于更高次幂。 但是,当这种计算方法同时出现在《总纲》的三次幂开方算法和《算法》的5、7 次幂“查表法”中,就足以说明此算法在“求初商次商共积”时的可行性。 同时,由于此法适用于3、5、7 次幂,这也说明此算法可适用于其他次幂。
因此,《比例》“未知法”中的三次幂开方算法虽然源自《总纲》,但清初算家在构造“未知法”的4—10 次幂开方算法时,则应该是在《总纲》三次幂开方算法的基础上,参考了《总纲》中异于“常法”的计算方法,以及《算法》对“相近小数”的使用方法。 而清初算家之所以在构造3—10 次幂“未知法”时采用了这种方法,主要可能出于两方面原因:其一,在保证数值准确的前提下,此法可以简化大量计算步骤。 其二,此法可以适用于任意次幂,有助于使“未知法”在处理高次幂时不至于特别复杂。
2.2 “未知法”对“第一廉汎积”与“次行之数”之会通
除了上述步骤7,《比例》“未知法”的步骤5、9 也与“常法”不同,这两个步骤求的是“次商廉法”和“三商廉法”,前者用于计算次商,后者用于计算三商。 由于这两个步骤的算法原理相通,因而在此先讨论步骤5。 以“未知法”三次幂开方算法的步骤5 为例,其计算方法为“初商自乘,3 因之”,所得之数“以除次商积,即定次商”。 此方法同样可以对应清初算家在平方法末尾处所作的“解释说明”,即“此法止用廉法除余积,得次商……与常法不同”。 但值得反思的是,这种异于“常法”的计算方法是怎么来的? 实际上,清初算家对这一计算过程应该并不陌生,因为此计算方法在《少广拾遗》中也曾出现过。
2.2.1 “未知法”“盖本法”与“诸乘方大法”
为了下文更好地探讨“未知法”对《少广拾遗》中计算方法的借鉴,有必要在此之前先对“未知法”与《少广拾遗》之关系作一个简要的说明。
清初算家在介绍完“未知法”之后(自三乘方开始),会紧随着“盖几乘方之本法,有……”的一段话,之后会再介绍一种计算方法(以下称此计算方法为“盖本法”)。 笔者以为,“盖”应表示推测,相当于“大约”“大概”,再考虑到“未知法”来源未知,且异于“常法”,故而认为,“盖几乘方之本法,有……”之后的“盖本法”应该是清初算家对前面“未知法”原本样貌的推测,因此,“盖几乘方之本法,有……”应解读为“大概此处‘几乘方’原本的计算方法应该是这样的……”①对比“盖本法”与“未知法”可知,“盖本法”中仅第一步计算过程与“未知法”步骤5、6 一致,其余均与“未知法”有异,且有很大的不同。 首先,二者所求关键数值的步骤不同,“盖本法”是先求“次商”,再求“次商廉隅之共积”,但是,“未知法”则是先求“次商廉隅之共积”,再求“次商”,二者正好相反。 其次,“未知法”和“盖本法”求“次商廉隅之共积”的方法不同。 “未知法”是用过“原积”-“初商积”的方法求得“次商廉隅之共积”;“盖本法”则是通过对“廉”“隅”做计算,再求“次商廉隅之共积”。 因此,进一步说,笔者认为“盖本法”仅是针对“未知法”步骤5、6 的原本样貌的测性解读,即主要针对开平方法后“解释说明”中“此法止用廉法除余积,得次商”的回应,而非“未知法”的全部流程。。
实际上,“盖本法”与《少广拾遗》“诸乘方大法”中求“廉隅共积”的计算方法非常相似,二者的区别在于乘以次商的时机不同。 “盖本法”是先求各廉和,再用各廉和一起乘以次商;“诸乘方大法”则是在计算每一廉的定积时,直接乘以次商。 二者有此区别的原因暂且不表,只有解决了之后的一系列问题,才能言明(原因分析见下文)。 但二者的相似性,以及梅瑴成等人对梅文鼎工作的熟悉,说明清初算家在构造“未知法”时,应该参考了《少广拾遗》中的“诸乘方大法”。
因此,清初算家应该是基于对“诸乘方大法”的了解,将其中的部分计算方法进行了适当的调整,才构造了“盖本法”,并在“未知法”之后,“盖本法”之前,给出“盖几乘方之本法,有……”的字样,表示对“未知法”本来样貌的推测②关于“盖本法”的作用及意义:清初算家在开平方法后曾指出“未知法”中的步骤5—8 与“常法”不同,而此计算方法能解决“廉法条例甚繁,难于布算”的实际问题。 因此,一方面,“盖本法”是对“廉法条例甚繁,难于布算”的实际演示,它能够展现“未知法”确实在“多乘方,所省实多”;另一方面,则是为了解释,为什么在“求廉法”和“次商”时,即“未知法”的步骤5、6,可以使用“止用廉法除余积得次商”的这种异于“常法”的计算方式。 笔者以为,第二方面是最重要的。。
然而,我们虽然考证了“未知法”“盖本法”与“诸乘方大法”之间的关系,但是本小节开篇所说的重要问题仍然有待解答,即这种“止用廉法除余积”的异于“常法”的计算方法是怎么来的? 它和《少广拾遗》又有怎样的关系?
2.2.2 《少广拾遗》中的“第一廉汎积”
《少广拾遗》的“开诸乘方大法”在求次商(或三商)时,需要用“汎积之和”与“余积”相除,但“汎积之和”的求法比较繁琐。 繁琐之处在于,不同次幂有不同数量的“廉”,不同“廉”求“汎积”值的方法又不同,最终需要求得每个“廉”的“汎积”值,再将它们相加,才能得到“汎积之和”。
“廉”的汎积值求法(图5)所示,其中最关键的两个数值为该“廉”的“定率”及其“应有各数”。 首先,随着乘方数的增加,“廉”的数量会增加,而不同次幂各“廉”的“定率”也有所不同,其数值源自“廉率立成图”([16],页5a),如立方有两个廉,第一廉的“定率”为3。 其次,各“廉”对应的“应有各数”也不同,如立方第一廉的“初商应有各数”即为“初商平幂”。 这两个数相乘便可得到立方第一廉的汎积值,即初商2×3,如果再求得立方第二廉的汎积值,将二者相加,便能基于此求得次商。

图5 各廉“汎积”计算流程
稍加留意便可发现,《比例》三次幂“未知法”的步骤5,即上文所述异于“常法”的计算方法,恰好与《少广拾遗》中三次幂第一廉汎积的计算方法相同,二者都是“初商自乘,三因之”。 无独有偶,这两个数值还都是为了求次商所用,只不过《少广拾遗》的计算更为繁琐,在处理更高次幂时,它除了要求第一廉的汎积值,还要求其他所有廉的汎积值。
再看“未知法”与“常法”的另一个不同之处,步骤9。 “未知法”(三次幂)为“初商、次商相并自乘,3 因之”,所得为“三商廉法”,用此数便可求三商。 再看《少广拾遗》求三商时的计算方法,同样需要计算“汎积之和”,但与上文求次商时略有不同的是,此时各廉“应有各数”的计算方法要改成带入“初商、次商相并之数”,即所谓“其廉定率不变,但求汎积时,三商则并初商、次商两位商数合而用之”([16],页18a)。 因此,《少广拾遗》在求三次幂的三商时,第一廉汎积的计算方法应为(初商+次商)2×3,此法与“未知法”的步骤9 完全相同。
可见,“未知法”(三次幂)求次商、三商时所需的“次商廉法”“三商廉法”的计算方法与《少广拾遗》(三次幂)求次商、三商时所用的部分内容(即第一廉汎积求法)完全相同,对比其他次幂(如4—10 次幂)同样如此。 因此我们说,“未知法”异于“常法”的“止用廉法除余积”的计算方法,极有可能是参考了《少广拾遗》的“诸乘方大法”。
但是,如果这种可能性是真实的,就引出了另一个问题,即清初算家在熟悉《少广拾遗》中“诸乘方大法”的基础上,为什么在构造《比例》的“未知法”时没有沿用熟悉的算法,而是使用了现在这种“止用廉法除余积”的计算方法呢? 他们是怎么确定,可以仅通过“诸乘方大法”的第一廉汎积,而非所有廉的汎积值的和,就能求得次商和三商呢? 他们是在什么情况下,意识到这种方法不仅能适用于《总纲》的三次幂开方算法,还能拓展并适用于更高次幂? 实际上,清初算家应该是对比了《算法》“查表法”使用的“数表”中的“次行之数”,才确认了此方法的可行性。
2.2.3 “第一廉汎积”与《算法》的“次行之数”
以《少广拾遗》解四乘方为例(x5=13383270465632,x=422),求三商时,其第一廉“定率”应为5,“应有各数”为424,因此,第一廉“汎积”的计算方法应为424×5=15558480。 而这一数值,恰巧和《算法》五次幂“查表法”所用“数表”中的“次行之数”相同,即求三商时所用的“三商廉法”。 同样的情况也发生在七次幂上,《少广拾遗》七次幂求三商时第一廉汎积的数值同样可以和《算法》七次幂“数表”相应表格的“次行数字”相对应。
因此,除了《总纲》中的三次幂开方算法在求次商、三商时所用的“次商廉法”“三商廉法”可以对应于《少广拾遗》中的第一廉汎积求法,《算法》中5、7 次幂“查表法”在求三商时所用的“次行之数”也能够对应于《少广拾遗》。 应该正是这种一致性,让清初算家确认并意识到,虽然这种计算方法仅等同于“诸乘方大法”的第一廉汎积求法,且与“常法”不同,但它仍然能够保证求次商廉法、三商廉法以及次商、三商时的准确性,以及对不同次幂的广泛适用性。 基于此,清初算家才能够将《总纲》中仅有的三次幂开方算法进行拓展,只需在不同次幂的步骤5、9 中使用这种异于“常法”的计算方法(表1),即可让“未知法”适用于更高次幂。
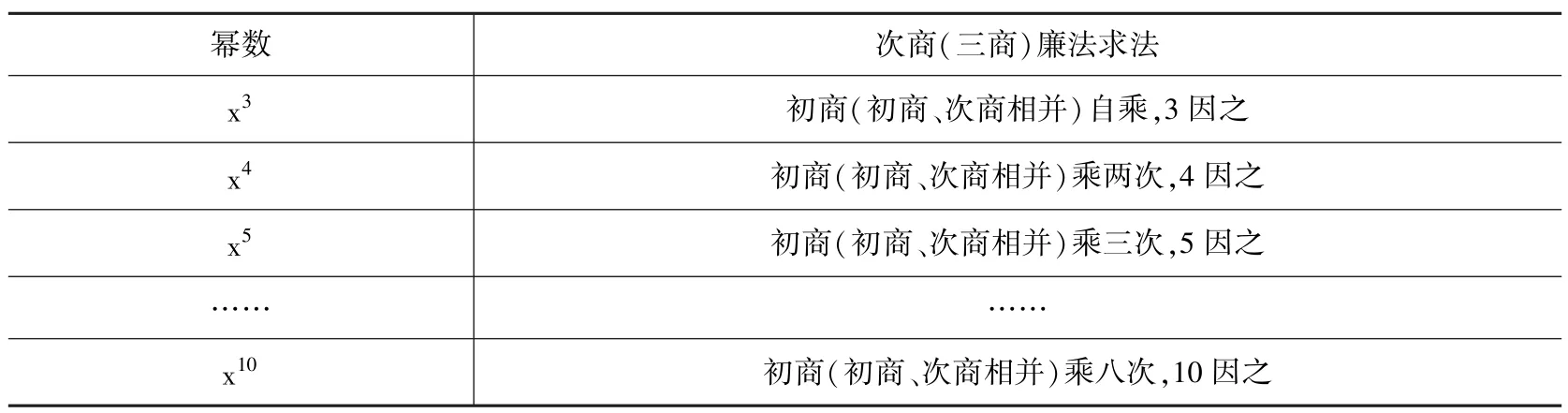
表1 《比例》“未知法”不同次幂次商、三商廉法求法
至此,我们也许可以对上述关于“盖本法”与“诸乘方大法”为何不同这一问题,尝试作出回应。
考虑到《数理精蕴》是一部西方数学著作的编译作品[17],所以“未知法”很可能是作为西方的开方算法来介绍的。 实际上,清初算家在构造出了“未知法”之后,就已经认识到了“未知法”与“常法”有异,出于某种原因,他们需要对这种异于“常法”的计算步骤作解释说明,因此,就需要借助某种熟知的开方算法,此时,梅文鼎的《少广拾遗》就派上了用场。 通过参考《少广拾遗》,清初算家对“诸乘方大法”中的部分计算流程进行了改编,构造了“未知法”之后的“盖本法”,以此试图对“未知法”中异于“常法”的部分算法进行解释,使其合理化;并在介绍“盖本法”之前,给出“盖几乘方之本法,有……”的字样,表示这是对“未知法”原貌的推测。 同时,此行为还能展现这种西方开方算法的“中源”特征,这与当时“西学中源”说的社会背景也是吻合的。
反观本小节之主题,虽然《比例》卷32 中的三次幂开方算法源自《总纲》,但是,卷32 中的4—10 次幂开方算法,以及整个“未知法”(3—10 次幂)则应视为中、西算法相互会通融合的产物。 首先,它展现了中算传统特征的术语和表达形式。 其次,清初算家基于对《算法》5、7 次幂“查表法”所用的“相近小数”和“次行之数”的理解,以及对梅文鼎《少广拾遗》“开诸乘方大法”的熟悉,才能以《总纲》中异于“常法”的三次幂开方算法为基础,将其拓展至3—10 次幂。 此外,“未知法”还展现了中算传统中的程序化、机械化特征(图6)。 经检验,它不仅可以处理《算法》所未及的更大数值,还可以适用于任意次幂,“但其数繁衍而无所用,兹故不载焉”([2],下编卷32 页3)。

图6 高次幂开方算法流程图
3 《比例》卷33 高次幂方程解法的“重构”与“创新”
在讨论《比例》卷33 中统一的3—6 次幂方程解法来源之前,首先要指出的是,卷33 中的三次幂方程解法的步算过程与《算法》是一样的。 如果用现代数学语言解读,两书中的解法都和“牛顿法”一样,也正因如此,才有《比例》三次幂方程解法源自西方之论断。
但是,两本算书中的三次幂方程解法还是有差异的。 首先,二者的表述方式不同,《算法》的步算过程是纯数值运算,安多仅介绍了各数值的使用方法,但并未对运算过程做任何解释,其中更没有任何中算传统术语。 《比例》则更像是对纯数值运算的解读,清初算家使用了大量中算传统术语,如“立方廉”“平方廉”“次商廉法”……来解释运算过程。 其次,《算法》中的高次幂方程(axn±bxm=c)均为多项式相乘之结果,它们属于纯数值运算,与几何图形无任何关系,但《比例》的编撰者却将它们视为不同的几何图形,并称得到这些几何体的过程为“变正方体而为长方体,或为磬折长方体、扁方体”([2],下编卷33 页12),体现了中算传统用图解方式说明数学问题的特点[18]。 此外,还不应忘记《算法》中3 次幂与4、6 次幂的方程解法并不相同,而《比例》中的3—6 幂次方程解法却带有中算传统的程序化、机械化特征。 因此,在探讨《比例》卷33 中高次幂方程解法的来源时,不应忽视其中算渊源。
如上文所述,在《比例》之前,《数理精蕴》卷24 就已经介绍了中算传统处理三次幂方程的“常法”,有学者认为《比例》卷33 中的三次幂方程解法即来源于此[3],但二者实际上并不完全相同(表2),且清初算家在《比例》中也曾直言称“借根方比例开带纵立方,与常法不同”([2],下编卷33 页10)。
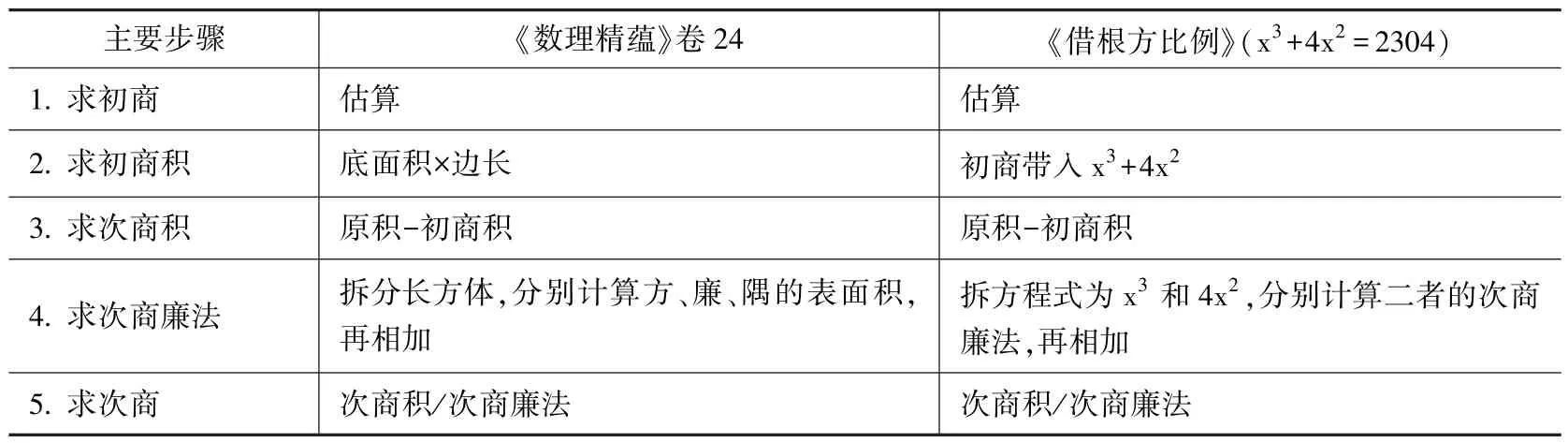
表2 《数理精蕴》卷24、《比例》三次幂方程解法步算流程对比
虽然两种算法的运算流程大体相同,都可分为“求初商、求初商积、求次商积、求次商廉法、求次商”5 个步骤,但二者对步骤2、4 的处理方式还是略有不同,这体现了“常法”与《比例》卷33 对同一运算法则的不同理解方式。
“常法”使用的是符合中算传统开带纵立方的图解方式,即将一个长方体递析开之,将其分为一个小长方体,以及包裹在它之外的“方、廉、隅”,求“次商”时,需分别计算“方、廉、隅”的表面积、体积,并以此求得次商(图7)。 然而,即便清初算家有了熟悉的“常法”,但他们并没有在《比例》卷33 中沿用此法,而是转而采用了《算法》中的三次幂方程解法。 究其原因,“常法”所处理的带纵立方问题总表现为某几类“常规”几何体,它们或为“长方体”或为“扁方体”,但《算法》中的方程是多项式相乘的结果,与几何图形并无关系。 因此,在清初算家看来,这些一元多次方程“或为长方体扁方体形,或非长方体扁方体形,皆不可知”,既然其样貌不可知,自然就“不可以带纵之常法求也”([2],下编卷33 页10)。

图7 “常法”图解与“新”图解
因此,清初算家为这些“不常规”几何图形“重构”了新的图解方式,以x3+4x2为例,他们借助中算传统“析理以辞,解体用图”的方法,把x3+4x2所代表的长方体分成了两个部分,称其为“正方体之外多四平方,故成长方体”([2],下编卷33 页17)(图7)。 求次商时,只需分别计算“正方体”(x3)和“四平方”(4x2)两者的“次商廉法”并相加(即步骤4),即可求得“次商”值,而“次商廉法”的计算方法则与《比例》“未知法”沿用《少广拾遗》第一廉“汎积”的计算方法相同(表1)。
至此,也可以对上文中提及的问题,即“既然《算法》的作者声称三次幂方程解法与《总纲》同,那么清初算家为何选择了《算法》,而非《总纲》”尝试作出回应。
依笔者浅见,清初算家选择沿用《算法》计算方法的原因在于,在求初商积时(步骤2):一,《总纲》将初商带入x2(x+a)的行为与中算传统的思路相同,此法在《数理精蕴》卷24 中已有体现。 二,《算法》将初商带入x3+ax2的方法具备将三次幂方程解法拓展至更高次幂方程解法的可能性。 三,《算法》将初商带入x3+ax2以求初商积的方法(步骤2),可以和之后步骤4 中将x3+ax2拆分为两个几何图形的图解方式保持一致性,而《总纲》却不能。
此外,清初算家还将这种新的“图解方式”应用于任意次幂,在处理高次幂方程时,即便它们的外形“皆不可知”,但只需根据不同次幂改变相应的“次商廉法”计算方法即可。如x5+2x3=7990272,同样是将其拆分为两个部分,即“四乘方”(x5)和“两个立方体”(2x3)([2],下编卷33 页37),然后分别计算二者的“次商廉法”即可(表1)。 与《比例》卷32 中的“未知法”一样,卷33 中的4—6 次幂方程解法同样展现了中算传统的程序化、机械化特征。
综上,《比例》卷33 中的三次幂方程解法一直是前人讨论的焦点,虽然它和西方的“牛顿法”类似,但它只是3—6 次幂方程解法的其中之一,如此,《比例》卷33 中的高次幂方程解法(3—6 次幂)应该被视为一个整体进行讨论。 通过上述对比、复原、分析,可知清初算家沿用了《算法》中的三次幂方程解法,并基于中算传统的图解方式对此算法作了“重构”与“创新”,又参考了《比例》卷32“未知法”中源自《少广拾遗》第一廉汎积的“次商廉法”的求解方式,才构造出了这套新的带有程序化、机械化特征的高次幂方程解法。
4 余论:对清初算家会通行为的反思
《比例》卷32 的高次幂开方算法(“未知法”)(xn=a)、卷33 的高次幂方程解法(axn±bxm=c)的来源如图8。 虽然卷32 中的三次幂开方算法源自《总纲》,卷33 中的三次幂方程解法源自《算法》,但是,将这两个算法改编成一套程序化、机械化的算法流程,并将其拓展、适用于更高次幂的工作应是清初算家“会通中西”的一个创造性成果,并非单独源自中、西二者之一。

图8 《比例》卷32、33 开方法来源分析
值得反思的是,《算法》中的高次幂开方算法和高次幂方程解法原本并非全书的重点内容①其一,安多尽量使用开平方、开立方的“换元法”来解决这些开方问题。 其二,在“借未知数—列式—化简—开方”这一运算流程中,简单问题经过“化简”步骤后便能直接得到最终结果,只有复杂问题(即化简后等式为xn=a 或axn±bxm=c)才会涉及这些算法。 其三,在《算法》的删减本《借根方算法节要》中,安多仅删减了对高次幂开方算法的介绍。 其四,傅圣泽在介绍《阿尔热巴拉新法》时,介绍了西方代数学的符号表示法、等式的概念,唯独没有介绍开方算法。,但为何清初算家要在《比例》中称赞“借根方比例法中,开各乘方为最要”,并做这般创造性的改进工作呢? 究其原因:
其一,开方算法一直以来都是中国传统数学最为擅长的运算法则之一。 从《九章算术》首次给出开平方法与开立方法,到《孙子算经》对开方算法“超位退位定位”的改进……到南宋的贾宪给出了“增乘开方法”,以及刘益、秦九韶等人对“增乘开方法”的改进,可见开方算法在中国本就有深厚的土壤基础。
其二,康熙对开方算法有较高的关注度。 在面对傅圣泽(Jean-François Foucquet,1665—1741)的“新代数学”(符号代数)时,康熙非但没有理解这些数学知识的重要意义,在评价傅圣泽的“算法平平”时,他还不忘转而称赞《算法》中的开方算法([6],页25)。当得知西洋人戴进贤(Ignatius Kgler,1680—1746)带来了“简单讲述小计算之书几小本”[19]时,他也非常关注“此等人尚有新好法,或有简便计算数表,开方方法,即缮写带给朕”[19]。 由此可见康熙对开方算法的重视。
其三,与“西学中源”说相吻合。 自康熙在《御制三角形推算法论》中明确提出“西学中源”说后[20],历算学家通常会以此学说为基础,将西学纳入中算传统。 《数理精蕴》在开篇就描绘了中国古代典籍西传之图景([2],上编卷1 页10),清初算家更是在书中称西方的比例算法乃中算传统之质言([2],下编卷3 页3)……加之康熙曾称“阿尔朱巴尔,传自东方之谓也”[21](阿尔朱巴尔,algebra 音译,即指《算法》),这些宫廷数学家自然要将此观点付诸实践,在卷32“未知法”后接“盖本法”的行为就是一种体现。
相较于西方算法,《比例》卷32 中的高次幂开方算法(“未知法”)和卷33 中的高次幂方程解法不仅可以使用中算传统术语进行表达,它们还带有中算传统的程序化、机械化特征,展现了“中源”的影子,尤其是清初算家对“未知法”本貌的推测,更是建立了西方算法与梅文鼎《少广拾遗》之间的联系。 此外,因为清初算家的创造性工作,它们还可以处理更大数值和更高次幂。 相较于中算传统,由于借鉴了《算法》“数表”中的数值,《比例》卷32 的高次幂开方算法(“未知法”)和卷33 的高次幂方程解法可以在确保计算准确性的前提下,省略大量计算步骤,使算法流程甚是简捷。 总之,清初算家的会通行为无疑对中算传统的发展以及中西文化的交流都具有积极意义。

