计及维护操作影响的变压器内部潜伏性故障率预测模型
程欣,孙悦,黄威,廖庆龙,李轩,胡博,谢开贵
(1. 国网山西省电力公司经济技术研究院,太原 030000;2.重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆 400044; 3.国网重庆市电力公司电力科学研究院,重庆 404100)
0 引 言
油浸式变压器是电力系统的重要组成元件,其稳定运行是保证系统供电可靠性的基础[1]。变压器故障率是评估其可靠性的主要参数,及时准确地获知变压器实时故障率能够为调度运行、检修计划制定以及电网规划提供充分的依据[2]。因此,对变压器故障率进行预测建模成为当下研究热点之一。
变压器的故障可分为内部潜伏性故障和外部随机故障,两者在故障的发展模式上有所区别,因此,在故障率建模过程中,应该分开考虑这两种故障模式[3]。由于变压器的故障大多是由其内部器件老化引起的内部潜伏性故障[4],因此,研究侧重于建立可以表征变压器内部潜伏性故障的时变故障率模型。
变压器油中溶解气体的含量与其内部潜伏性故障严重程度存在着显著的对应关系,已经在变压器故障诊断与状态评估等领域得到了广泛的应用[5-6]。通过对油中溶解气体分析(dissolved gas analysis, DGA),可以及时了解变压器实时运行工况、掌握其内部潜伏性故障率的变化特征[7], 因此适合以油色谱监测数据(下称DGA数据)进行故障率建模。文献[8]基于小样本训练数据,利用最小二乘-支持向量机法对变压器故障率与油中气体含量、产气速率等特征量的关系进行拟合,以求解变压器实时故障率;文献[9]基于马尔科夫过程理论,建立了变压器时变停运模型,但是忽视了维护操作对变压器故障率的实际影响。文献[10]通过引入比例风险模型对变压器时变停运率进行建模,克服了监测间隔对故障率预测精度的影响,但是也未能有效表征维护操作影响。文献[1,4]为刻画维护操作的影响,在建模过程中进一步引入役龄,绝缘纸含水量等协变量,但是该类数据无法反映变压器实时的内部运行工况。同时,该类数据的获取依赖于复杂的加速老化试验,实际工况数据很难获得。事实上,短时间尺度下的DGA数据变化可以反映考虑维护操作影响的变压器短期故障率变化特征,但上述文献在建模过程使用的DGA数据来源较为单一,采样数据时间跨度大多超过数月[11]。近年来,随着大量的变压器在线监测设备安装、投运,DGA数据在内容广度以及采样时间频度上得到了很大地提升,电网已经积累了非常丰富的数据,呈现典型的大数据特征[12],因此,通过挖掘以天为采样单位的变压器DGA监测数据,提出了一种基于数据挖掘的变压器时变内部潜伏性故障率预测模型。
为了表征维护操作的影响,提出传统马尔科夫故障率模型中自变量状态持续时间进行修正。利用径向基函数(radial basis function,RBF)神经网络构建了表征油色谱监测数据输入与修正状态持续时间输出关系的映射模型;其中,为了避免各溶解气体间存在的相关性及溶解气体种类过多可能引起神经网络模型准确度不稳定的问题,采用R型聚类-主成分分析算法(R cluster analysis-principal component analysis, RCA-PCA)提取关键溶解气体种类,进而缩减神经网络输入维度。结合变压器多状态马尔科夫过程,得到了以修正状态持续时间的变压器时变故障率表达式。最后与传统变压器马尔科夫故障率模型进行比较,验证文中模型的优越性。
1 模型框架
依据上述思路,提出的变压器内部潜伏性故障率预测模型研究框架如图1所示。
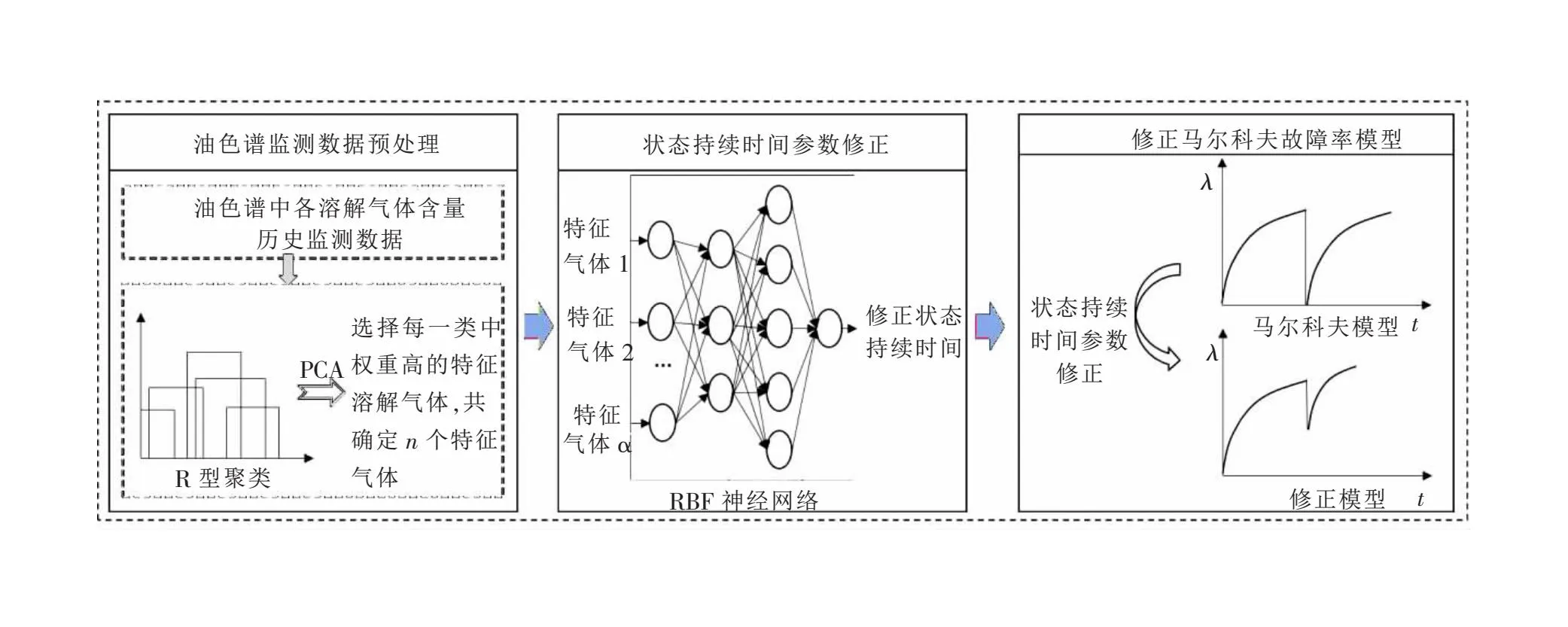
图1 变压器内部潜伏性故障率预测模型研究框架
在不计及变压器DGA状态监测系统装置异常或错误的前提下,对油浸式变压器的内部潜伏性故障率进行预测建模的基本步骤如下:
步骤1:首先对维修前的变压器的DGA溶解气体进行预处理,基于RCA-PCA提取关键溶解气体。以维修前的关键气体含量作为输入,对应的状态持续时间作为输出,构建RBF神经网络的训练样本;
步骤2:选择合适的核函数,将训练样本输入RBF模型中,建立输入与输出间的映射关系。此时输出也为修正的状态持续时间;
步骤3:基于修正的状态持续时间,对传统马尔科夫故障率模型进行修正,得到考虑维护操作影响的故障率解析表达式;
步骤4:输入实时的变压器关键溶解气体含量监测数据至故障率修正模型中,获取此时对应的内部潜伏性故障率预测值。
2 马尔科夫故障率模型
作为一个典型的可修复元件,油浸式变压器的运行工况一般在良好、警告、危险及故障四个状态间转移[13],具体转移过程如图2所示。
图2中所描述的变压器各状态转移过程符合典型的马尔科夫转移,因此,图2也称为变压器的马尔科夫多状态转移图。由图2可以看出,变压器在自然运行过程中存在明显的内部恶化过程,但维护操作可使其恢复到前一个状态或是初始良好状态[14]。其中,wi,j表示变压器从状态i到状态j的转移速率,wi,j=1/yi,yi为变压器运行在状态i的持续时间,也称为状态持续时间。
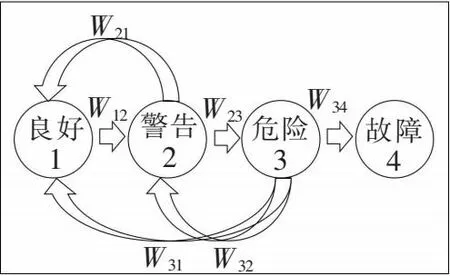
图2 变压器运行状态转移图
基于上述马尔科夫转移过程得到的转移速率矩阵如下所示:
(1)
假设变压器在t时刻运行在各状态的概率为:P(t)=[P1(t),P2(t),P3(t),P4(t)],初始运行状态为P(0)。则依据文献[4]给出的马尔科夫故障率求解方法,可以求得t时刻变压器的内部潜伏性故障率λ(t)等于P4(ti)。其中,ti为变压器在t时刻已运行在状态i的持续时间,也称为t时刻对应的状态持续时间。
图3给出了基于上述模型得到的变压器内部潜伏性故障率随时间变化的曲线。
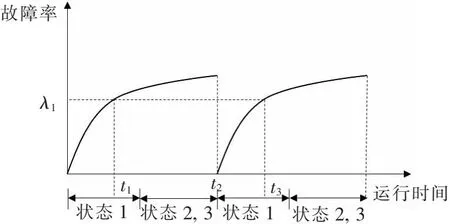
图3 变压器故障率变化图
如图3所示,变压器在t2时刻经历维护操作后,重新返回状态1。由于t1与t3处于状态1的持续时间相同,此时得到的两个时刻对应的故障率值也相同。在实际中,由于维护操作不可能使得变压器重新返回状态1的初始时刻,因此t1与t3时刻的故障率应该有所区别。但是,该模型中的自变量状态持续时间仅考虑了变压器在所处时刻的运行状态与运行持续时间,忽略了可以量化维护操作影响的变压器实时运行工况信息。事实上,在准确量化维护操作影响后,相较于t1时刻,t3时刻的故障率应该有所增加[8],因此,该状态持续时间需要被修正,具体修正方法将在下一节介绍。
3 马尔科夫故障率修正模型
油色谱实时监测数据可以准确反映变压器的运行工况,因此,选择以天为单位的油色谱数据作为建模基础,对马尔科夫故障率模型中的状态持续时间进行修正。由于油色谱监测信息与修正状态持续时间之间存在典型的非线性关系,因此采用RBF神经网络建立油色谱监测信息与修正状态持续时间的映射关系。针对输入溶解气体种类过多以及各气体间高相关性可能会引起RBF模型结果不稳定的问题, 提出一种基于RCA-PCA算法的关键溶解气体筛选方法。
3.1 基于RCA-PCA的关键溶解气体提取
3.1.1 基于RCA的溶解气体聚类
RCA是一种典型的多元统计分析方法,已被广泛应用于变量聚类[15]。通过RCA将相关性高的溶解气体聚为同一类。其中,为了克服各溶解气体含量取值标准的差异性,选择平均相关系数作为各溶解气体间的相关性度量标准[15]。
假设有N组变压器油色谱历史数据作为训练样本,每组样本具有L种溶解气体,那么第n组监测数据(1≤n≤N)可以表示为:
Sn=(Sn1,Sn2,……SnL)
(2)
由训练样本得到的第q种与第r种溶解气体(1 ≤q≤L, 1 ≤r≤L)的归一化后取值集合可以表示为:
(3)
则表征第q种与第r种溶解气体之间相关程度的平均相关系数gq,r如下所示:
(4)
du,v=xup-xvq
(5)
可以看出,平均相关系数relq,r等于Xq与Xr中两样本点间欧式距离的平均值。其取值范围为[0,1]。relq,r越大表示两种溶解气体间的相关性越高;反之,两种溶解气体间的相关性越低。
设L种溶解气体被聚为K类,则任意两个气体聚类集合GA与GB间的距离Dis(GA,GB)可以由最大距离法计算:
(6)
disa,b=1-rela,b
(7)
此时,Dis(GA,GB)与两个聚类集合中相关性最小的两个溶解气体间的相似性度量值有关。利用上述指标,基于RCA的溶解气体聚类过程如图4所示。
上述溶解气体聚类方法按照各气体间的相关关系把它们聚成若干类,为下一步基于PCA提取每一个聚类集合中的关键溶解气体奠定了基础。
3.1.2 基于PCA的关键溶解气体提取
PCA是数据挖掘中一种高效的降维算法[16],文中借助PCA确定每一个聚类集合中各溶解气体的影响权重,通过保留高权重的溶解气体,删除其他溶解气体的方式实现对关键溶解气体筛选。
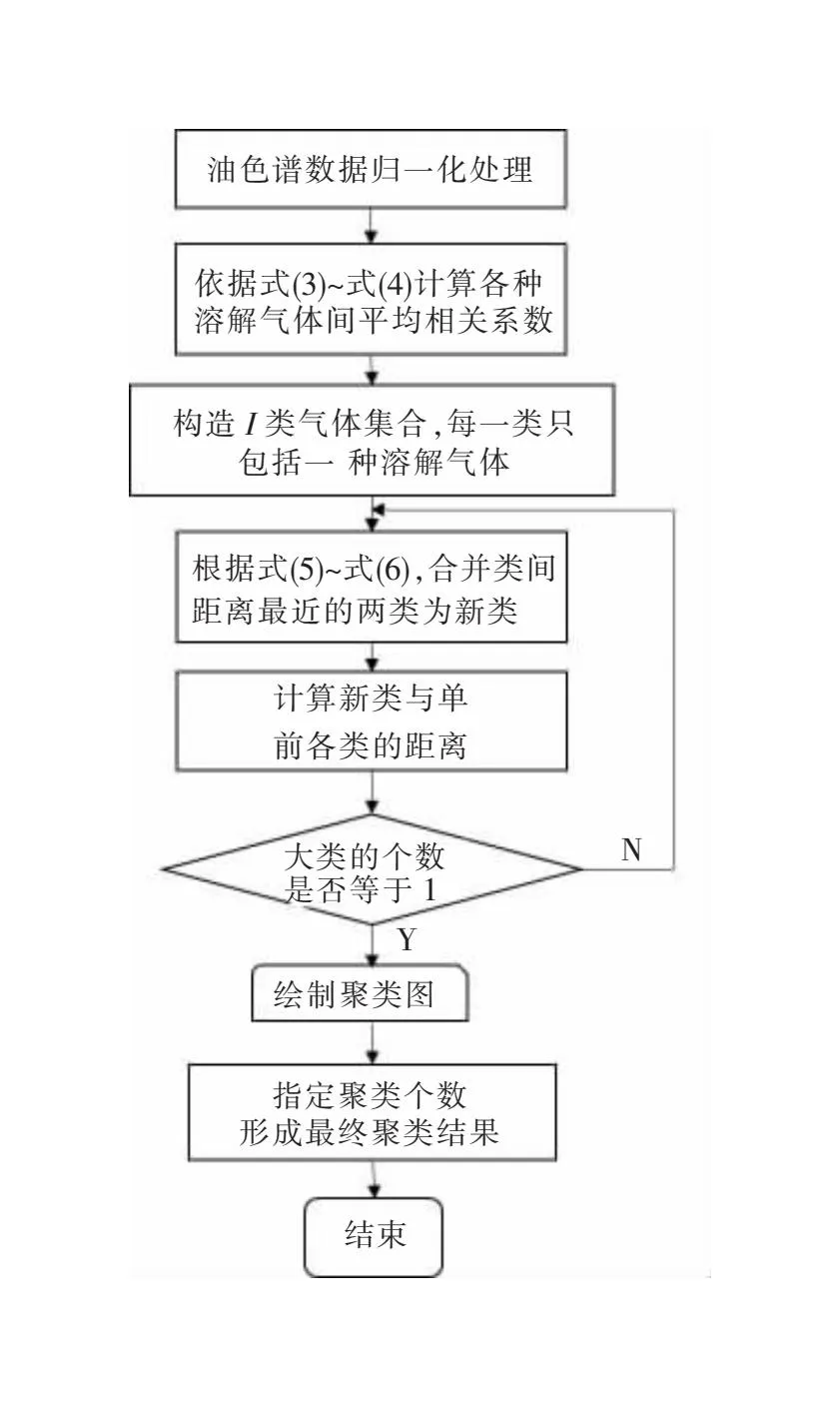
图4 基于RCA的溶解气体聚类过程
设第k个气体聚类集合内包含F种溶解气体。由于PCA的结果受到各种溶解气体含量数量级差异的影响,采用Min-Max标准化方法对油色谱数据进行标准化处理[16-17],具体如下所示:
(8)
式中 1 ≤f≤F, 1 ≤o≤N。xfo为第f种溶解气体在第o天的监测值,x′fo为标准化处理后的监测数值。
应用PCA进行各聚类集合中关键溶解气体筛选的具体步骤如下所示:
Step 1: 依据式(8)对油色谱监测数据进行标准化处理;
Step 2: 分析标准化油色谱监测数据之间的相关关系密切程度,以Person相似度为指标建立相关系数矩阵;
Step 3: 计算相关系数矩阵的特征根与特征向量;
Step 4: 分析各个主成分的贡献率,选择累积贡献率达到85%及以上的主成分种类与个数;
Step 5: 计算各个主成分与原始指标的相关系数(因子载荷量),进一步解释各主成分的含义;
Step 6: 主成分分析表达式分解,确定各个溶解气体的权重占比;
Step 7: 指定关键气体个数,依次选择权重大的溶解气体作为关键溶解气体。
3.2 变压器状态持续时间修正
径向基函数(RBF)神经网络是一种应用广泛的函数逼近工具,能够以任意精度逼近任意的非线性函数,性能优于现有的浅层神经网络(如标准反向传播神经网络等)[18-19]。因此,基于RBF神经网络建立关键溶解气体数据与其修正的状态持续时间之间的输入输出映射关系。RBF神经网络训练的具体结构如图5所示。

图5 RBF神经网络结构图
在变压器未经历维护操作前,其状态持续时间不需要修正,即认为变压器维护前的状态持续时间与其修正的状态持续时间相同。因此应选择未经历维护操作之前的关键溶解气体信息及对应的状态持续时间作为RBF模型的训练样本。设该神经网络输入层节点数为α,输出层节点数为β。输入层的输入INPUT可以表示为:
(9)
式中α为关键气体个数。同样,输出层的输出OUTPUT可以表示为:
(10)
设隐含层中有γ个节点数,则输出层第η个神经元网络输出可以表示:
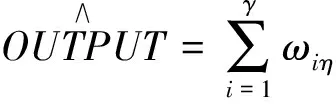
(11)
式中ωiη为确定的隐含层第i个神经元与输出层第η个神经元的连接权值。i(INPUT)为隐含层第i个神经元的作用函数,采用高斯函数作为作用函数,如下式所示:
(12)
式中Ci表示RBF神经网络的第i个基函数的数据中心;σi为其对应的方差参数。当ωiη、Ci以及σi通过训练过程确定后,给定一组变压器关键气体监测数据就可以求出网络输出的修正状态持续时间值。
依据本节提出的方法对t时刻变压器的状态持续时间进行修正,ti为该时刻对应的状态持续时间,此时修正的状态持续时间为t′i。结合第三节介绍的马尔可夫故障率模型,基于修正模型求得的t时刻变压器发生潜伏性故障的故障率λ(t)=P4(t′i)。
4 算例分析
以西南地区某电力公司多台110 kV油浸式电力变压器的油中溶解气体含量监测数据,对所提出的变压器内部潜伏性故障率模型进行了分析验证。表1给出了某台变压器部分的油色谱历史监测数据,由表1可以看出,变压器油中溶解气体包括氢气、乙炔、甲烷、乙烷、乙烯、一氧化碳、二氧化碳、总烃等8种溶解气体。

表1 变压器油色谱历史监测数据
4.1 关键溶解气体提取
利用所给出的RCA聚类算法,依据各溶解气体之间相关度对其进行聚类,得到的聚类图如图6所示。
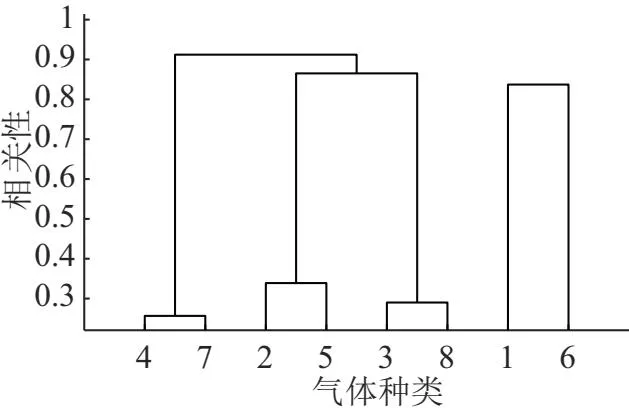
图6 八种溶解气体的聚类图
根据图6,可以得到不同聚类数目时的溶解气体聚类结果。如表2所示。

表2 聚类结果比较
由表2可以看出,当气体聚为2类或者4类时,容易出现各类包含的气体数目不均匀或数目过少的情况,不利于进行主成分分析。因此,选择将八种溶解气体聚为3类。第一类为乙烷、二氧化碳;第二类为氢气、一氧化碳;第三类为乙炔、甲烷、乙烷、二氧化碳。
对每一类包含的溶解气体进行主成分分析,选择权重大的溶解气体作为该类的关键溶解气体。具体的分析结果如表3所示。
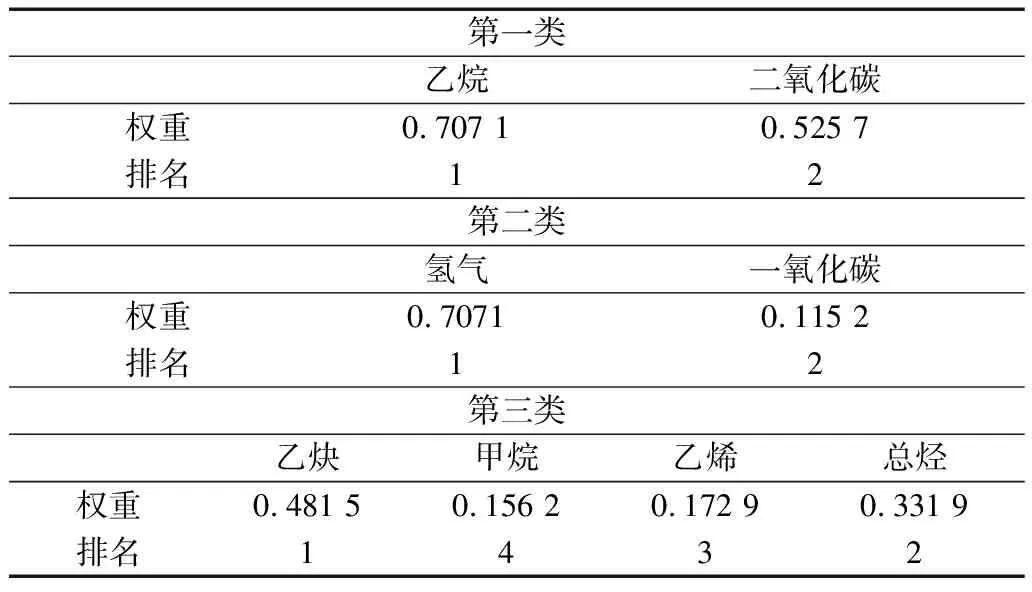
表3 PCA分析结果
由表3可以看出,在第一类中,乙烷的权重是二氧化碳权重的1.35倍,因此选择乙烷作为第一类的关键气体。同理,可以选择氢气作为第二类的关键气体,由于第三类气体种类数目较多,且乙炔和总烃的权重明显大于甲烷和乙烯所占的权重,因此同时选择乙炔与总烃作为该类的关键气体。结合文献[13]指出的甲烷与氢气、乙烷与甲烷、乙烯与乙烷、乙炔与甲烷间分别存在较高的相关性,基于关键气体选择方法得到的结果恰好避免了同时选择高相关性气体这一问题,从侧面验证了所提出的RCA-PCA方法的正确性与有效性。
4.2 马尔科夫故障率修正模型验证
为了刻画维护操作对故障率的影响,选取某台变压器从2016年12月24日~2017年1月7日这一期间每日油色谱监测数据作为故障率建模数据。需要指出的是,该台变压器在2016年12月24日经历了维护操作,这也意味着,在这之后,该台变压器的状态持续时间已无法反映其实际运行工况,因此需要被重新修正。表4给出了该台变压器在这一期间内的每日对应的状态持续时间、等效状态持续时间以及运行状态等运行参数。
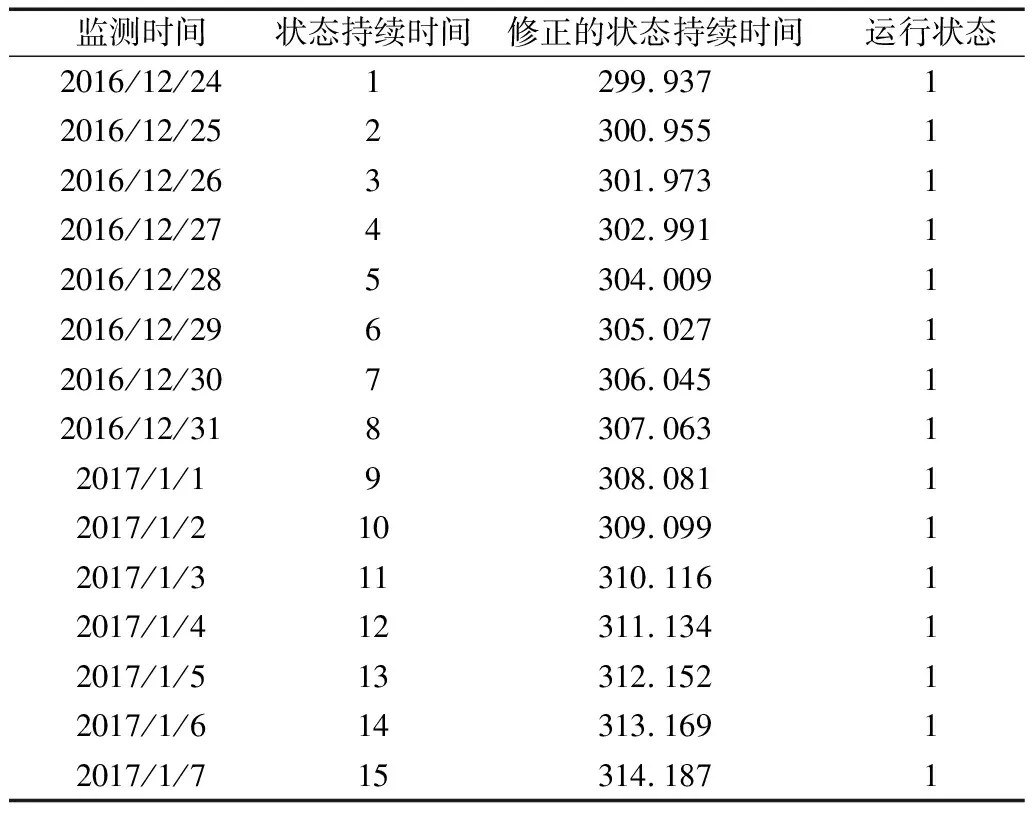
表4 变压器运行参数对应表
由表4可以看出,基于提出的模型,经历维护操作的变压器在2016年12月24日处于状态1,其实际工况相当于在状态1已经运行299.937天。而传统马尔可夫模型则认为变压器在2016年12月24这一天的运行工况应该是处于状态1的第1天,具体的原因已经在第2节进行了分析。
基于两种模型对这一期间内的变压器内部潜伏性故障率进行计算,结果如图7所示。
由图7可以看出,经过维护操作后,马尔科夫故障率模型得到的故障率值远远小于文中模型得到的故障率。这是由于文中的模型认为,尽管维护操作可以降低变压器故障的发展程度,但不能将变压器修复到某一状态的初始运行时刻。
本算例也着重分析了维护操作对变压器故障率的影响程度。维护操作引起的变压器故障率增量是文中模型得到的故障率值与马尔科夫模型得到的故障率之差。2016年12月24日~2017年1月7日这一期间内每天的变压器故障率增量如图8所示。
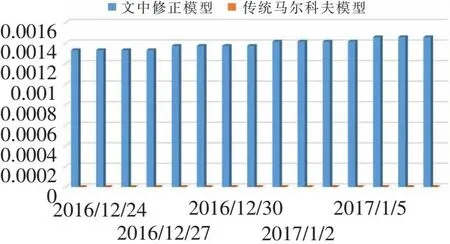
图7 变压器内部潜伏性故障率对比
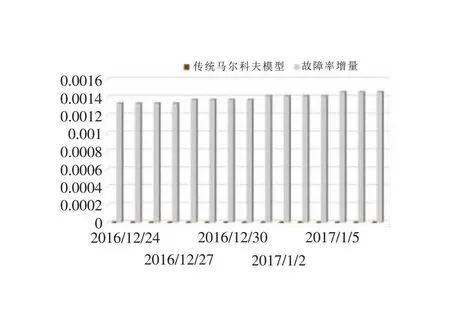
图8 变压器内部潜伏性故障率增量
由图8可以看出,两种模型计算出的故障率存在巨大的差异,基于两种模型得到的故障率增量值远远大于传统马尔可夫模型故障率值,这说明维护操作对于变压器故障率的影响不可以忽视。若故障率计算中不考虑变压器维护操作的实际影响,将会导致对于变压器状态评估结果过于乐观,进而给系统运行带来更大的风险。
5 结束语
文章对变压器油色谱监测数据进行深入的分析与挖掘,建立了一个基于数据驱动的变压器内部潜伏性故障率预测模型,有效地考虑了维护操作的影响。利用RBF神经网络建立了变压器修正状态持续时间与其监测数据间的非线性映射,结合马尔可夫状态转移过程,推导得到了故障率关于修正状态持续时间的解析表达式。其中,通过RCA-PCA算法提取了关键溶解气体种类,保证了神经网络输出结果的稳定性。所提出的模型进一步拓展了变压器内部潜伏性故障率的建模思路,可以对设备运行状况进行更加合理的分析、评估,有助于电网系统运维人员做出科学的检修决策。事实上,在监测数据传输过程中,容易发生数据缺失等问题,后续研究可从缺失数据修补等方面展开,基于已有的海量数据研究有效的缺失数据修补方法,进一步提升建模数据的质量,进而提高故障率建模的精度。

