随机丢包的无迹卡尔曼滤波估计以及性能分析

白 睿,任 祝

(1.浙江理工大学 计算机科学与技术学院,浙江 杭州 310018;2.浙江理工大学 信息科学与工程学院,浙江 杭州 310018)

无线网络控制系统(Wireless Network Control Systems,WNCS)是一种集成控制系统,不同的部件通过网络进行通信。该网络融合了计算元素、通信网络和控制系统,广泛应用于交通设施、信息通讯、人工智能、航空航天、军事管理和农业自动化等领域,是控制领域的研究热点之一[1-2]。在无线网络控制系统中,在传感器、设备和控制器之间利用无线网络控制系统传输数据具有较多优点,例如减少布线、灵活性以及可伸缩性等,但也存在网络诱导时延、时序错乱、数据丢包、选取采样周期、节点驱动等问题,不仅影响系统的控制性能,还降低了控制系统的稳定性。因此,需要构造估计器来估计网络当前的状态。

文献[3]提出了最优卡尔曼滤波分散化计算方法。文献[4]通过实验证明了分布式卡尔曼滤波器与集中式卡尔曼滤波器在数值上的等价性。当系统资源有限时,文献[5～6]为传感器节点的通信能力和计算能力之间的权衡提供了一种优化方法。文献[7]针对卡尔曼滤波安全状态做了性能分析和估计。文献[8]研究了卡尔曼滤波的间歇性观察的执行问题。文献[9]研究了网络中丢包的卡尔曼滤波,并使用两个状态马尔可夫链来描述正常操作条件的数据包传播状态。文献[10]考虑了在分组网络过程中的离散状态估计问题。文献[11]提出将两种算法与单个卡尔曼滤波器结合使用,以此估计系统状态和系统量测丢失。针对实际应用中存在的网络丢包问题,文献[12～15]研究了线性系统中有连续丢包和测量时延的卡尔曼滤波算法。

在实际问题中,过程模型预测和观测模型更新中的误差不容易利用对称、良好的高斯分布来描述。此外,过程和观察模型本身在状态下可能非线性,甚至非平滑,使传统卡尔曼滤波在频率检测预测方面存在困难。因此,文献[16～17]提出了扩展卡尔曼滤波(Extended Kalman Filter,EKF),后来研究者又对其进行了补充研究。但因为扩展卡尔曼滤波在线性化过程中舍去了高阶项,故其对强非线性系统估计精度较差。扩展卡尔曼滤波必须求解非线性系统的雅克比矩阵,当系统模型复杂时,计算量大、复杂且容易出错,从而限制了EKF的进一步发展。

为了克服上述扩展卡尔曼滤波问题,能够以较高精度和较快计算速度处理非线性系统的滤波问题,文献[18]根据确定性采样的基本思路,基于无损变换方法提出了无迹卡尔曼滤波(Unscented Kalman Filter,UKF)算法。无迹卡尔曼滤波算法并未采用对非线性函数进行线性化的传统方法,而是在传统卡尔曼滤波的框架下利用无损变换方法对一步预测的均值和误差协方差矩阵进行非线性传递。对于满足高斯分布的系统,精度可以达到3阶。基于改进的无迹卡尔曼滤波,文献[19]设计一种分布式协同定位方法。文献[20]基于无迹卡尔曼滤波研究了通信受限的无线传感器网络上非线性系统的远程状态估计问题。文献[21]考虑了一类不满足高斯分布的非线性离散随机系统,研究了具有相关噪声和随机丢包的无迹卡尔曼滤波算法。

本文研究了一类传感器测量值随机丢失的非线性离散系统的无迹卡尔曼滤波算法。首先,采用一步测量作为补偿器去代替零输入对系统状态进行估计;其次,选择两次Sigma点集进行计算,提高了无迹卡尔曼滤波的估计精度;最后,给出了相关算例验证本文所提滤波算法的有效性和可行性,同时比较分析了其在不同丢包率下的系统估计性能。

1 问题描述

经典无迹卡尔曼滤波算法打破了对非线性函数进行线性化的传统做法,在传统卡尔曼滤波的框架下利用无损变换方法对一步测量的均值和误差协方差矩阵进行非线性传递。其动态系统模型为

xk+1=fk(xk)+wk

(1)

zk=h(xk)+vk

(2)

其中,xk+1∈n是系统在k+1时刻的n维状态向量;zk∈n是传感器在k时刻的m维观测向量输出;f(·)和h(·)分别表示系统的非线性状态转移函和观测函数;过程噪声wk∈n和观测噪声vk∈n是不相关的零均值的高斯噪声向量,表示实数的集合;n表示n维欧几里德空间。

(3)

式中,E[·]表示随机变量的数学期望;协方差分别为Qk和Rk;δk-l是Kronecker函数,当k=l时取值为1,反之取值为0。满足

(4)

无迹卡尔曼滤波估计利用无损变换方法对一步测量的均值和误差协方差矩阵进行非线性传递。经典无迹卡尔曼滤波有以下几种形式。

(5)

以上为在系统理想情况下系统模型以及无迹卡尔曼滤波器。当数据正常传输时,无迹卡尔曼滤波估计器才能安全运行,在发生传感器测量值丢失时,无迹卡尔曼估计器无法得到正确的系统状态估计。

2 丢包补偿的无迹卡尔曼滤波器

2.1 系统模型设计

现有考虑的信息物理系统由一个非线性系统组成,当出现丢包时,系统模型为

xk+1=fk(xk)+wk

zk=h(xk)+vk

(6)

其中,xk+1∈n为k+1时刻的状态向量;zk∈n为k时刻的观测向量输出;yk∈n是k时刻来自滤波器的实际测量向量;f(·)和h(·)分别表示系统的非线性状态转移函数和观测函数;过程噪声wk∈n和观测噪声vk∈n是不相关的零均值的高斯噪声向量,协方差分别为Qk和Rk;λk∈服从伯努利分布的独立随机变量,表示k时刻是否发生丢包。

(7)

(8)

(9)

2.2 丢包补偿方案

由于环境变化和通信网络的不可靠性等因素,通信网络中普遍存在相关噪声和数据包丢失的现象。因此,本文考虑具有相关噪声和丢包的非线性离散随机系统。为了进一步提高系统滤波估计的精度,与不考虑噪声相关性的已有结果相比,本文提出了一步测量作为补偿器去代替零输入并设计了最优一步测量无迹卡尔曼滤波估计器。

滤波算法步骤如下:

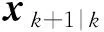
(10)

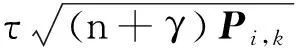
步骤2计算系统的一步预测协方差

(11)

(12)

步骤3基于系统一步测量值做第二次无迹变换,得到新的Sigma点集为

(13)

步骤4对新Sigma点集作观测非线性变换,得到

(14)

(15)

步骤5计算系统预测阶段的更新协方差矩阵Pyk+1|kyk+1|k以及互相关矩阵Pxk|kyk+1|k

(16)

(17)

步骤6计算更新后的增益矩阵和估计和协方差矩阵,如下所示。

Kk+1=λPxk+1|kyk+1|k(λPyk+1|kyk+1|k+λRk+1)-1

(18)

(19)

(20)

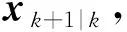
2.3 系统状态估计算法

为了检测本文所提最优补偿算法的性能,对发生丢包时最优一步测量无迹卡尔曼估计器的状态估计算法进行研究分析,无迹卡尔曼滤波器在丢包下进行去噪声处理得到的预测更新算法。

2.3.1 预测过程

基于式(6)～式(11)可以推导出状态估计器的先验估计值、先验误差和先验误差协方差分别如式(21)、式(22)、式(23)所示。

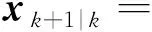
(21)

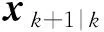
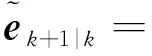
(22)

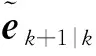
(23)

(24)

状态估计器在丢包下计算估计值时,先验估计值受到上一时刻后验估计值的影响,先验误差协方差受到上一时刻后验误差协方差影响,故在此基础上进行更新过程。

2.3.2 更新过程

根据上述预测得到丢包时的先验估计值和先验误差协方差矩阵,可以得到攻击下卡尔曼滤波器的最优增益

Kk+1|k=

Rk+1)-1

(25)

依据攻击下的最优增益更新当前k时刻的后验估计值、后验误差、后验误差协方差,如(26)、式(27)、式(28)所示。

(26)

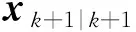
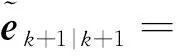
(27)

(28)

对比式(3)可知,在发生丢包时与系统安全稳定运行时后验误差协方差的区别。

通过举例方式对上述数据补偿进行说明,表1为量测数据zk的传输情况以及对应时刻数据补偿后的yk。

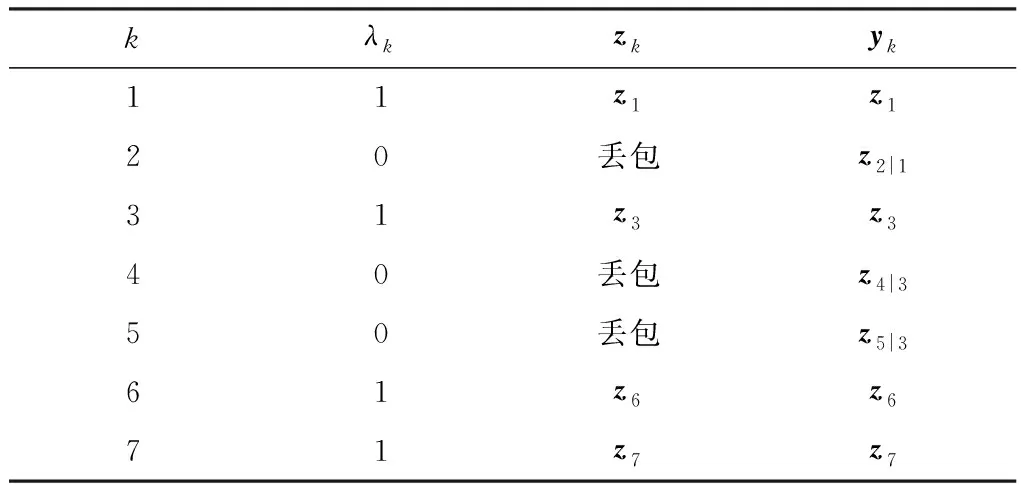
表1 数据传输图Table 1. Data transmission diagram

由表1可以看出,在系统工作k∈[1,7]时间段内,测量值z1、z3、z6、z7成功传输,而测量值z2、z4、z5丢失,其中z4、z5连续出现传感器测量值丢失。在实际情况中,由于系统估计存在一定估计误差,随着丢包次数的累加,其误差也将多次累计。

3 系统仿真和实验分析

为了验证理论的准确性以及有效性,仿真实验将发生丢包的估计值与未受到任何影响的真实值进行比较,系统选择的具有非线性系统状态方程构建仿真模型如下所示。

状态函数为

(29)

观测函数为

zk=x2,k-e-5x2,kx3,k+vk

(30)

其中,e为欧拉数;状态函数噪声为wk,其协方差Q=0.01I3;测量方程噪声为vk,其协方差R=0.01I1。

给出如下初始值

(31)

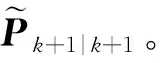
图1 UKF估计值与真实值的对比Figure 1. Comparison between estimated value and real value of UKF

图2 丢包发生时刻Figusre 2. Time of packet loss

图3 UKF估计误差Figure 3. Estimation error of UKF

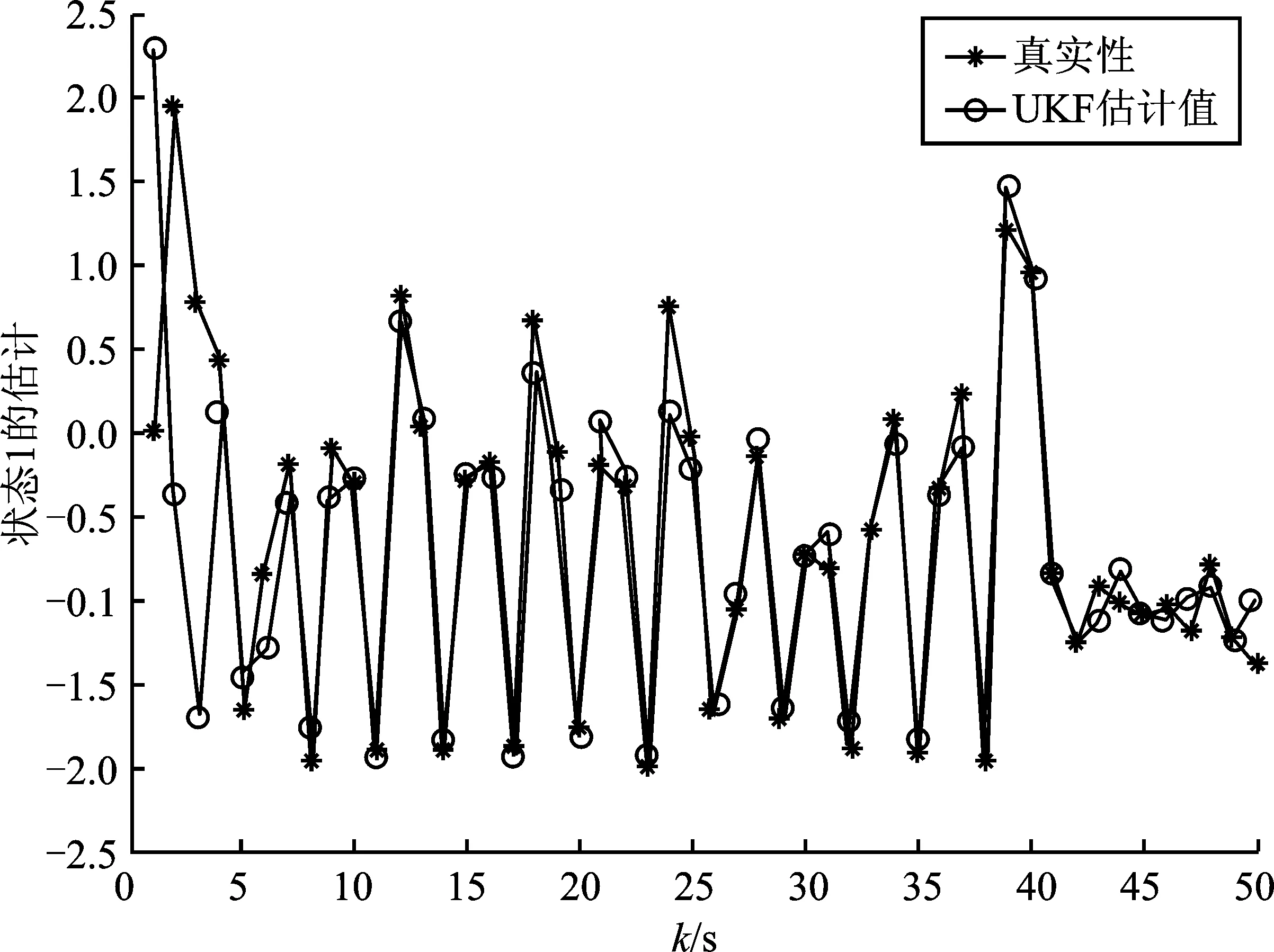
图4 x1,k和轨迹Figure 4. Trajectories of x1,k and

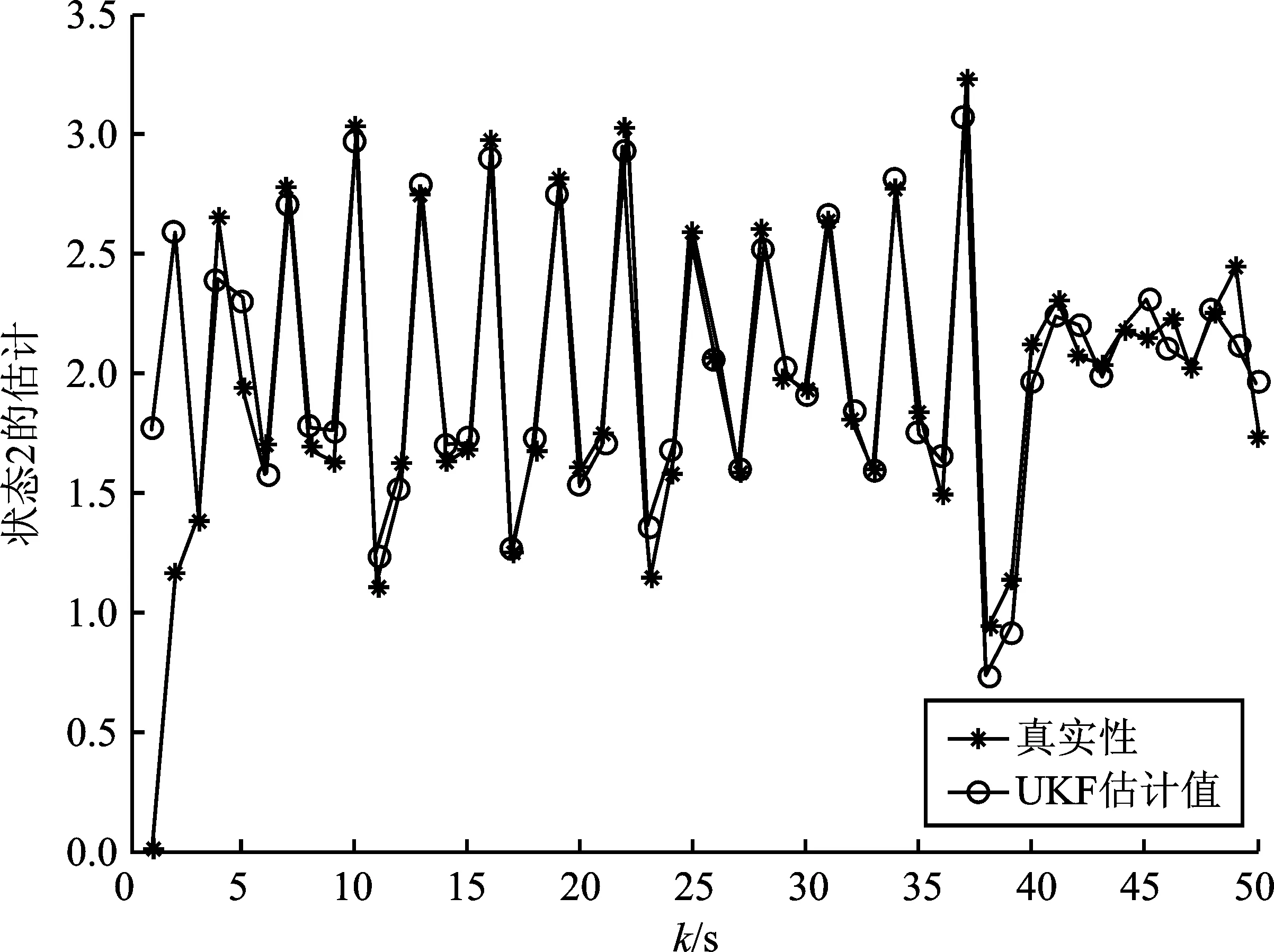
图5 x2,k和轨迹Figure 5. Trajectories of x2,k and

图6 x3,k和轨迹Figure 6. Trajectories of x3,k and

假设在固定窗口中,传感器进行随机丢包,模拟从k=0到k=50结束,选取的系统丢包率α=15%。由图1可以看出,随着系统不断运行,在该算法机制下估计值与真实值基本一致。由图2和图3中可以看出,估计误差偏差多为系统丢包处,有丢包时误差增大,当经过算法补偿后误差又迅速回落。通过对比系统状态和UKF估计值可以看出,经过算法补偿后的滤波能够较好地估计系统。

采用不同数据丢失率,即α为25%和35%时分析比较其对滤波器性能的影响。仿真结果如图7～图9所示。

图8 x2,k轨迹对比Figure 8.Trajectory comparison of x2,k

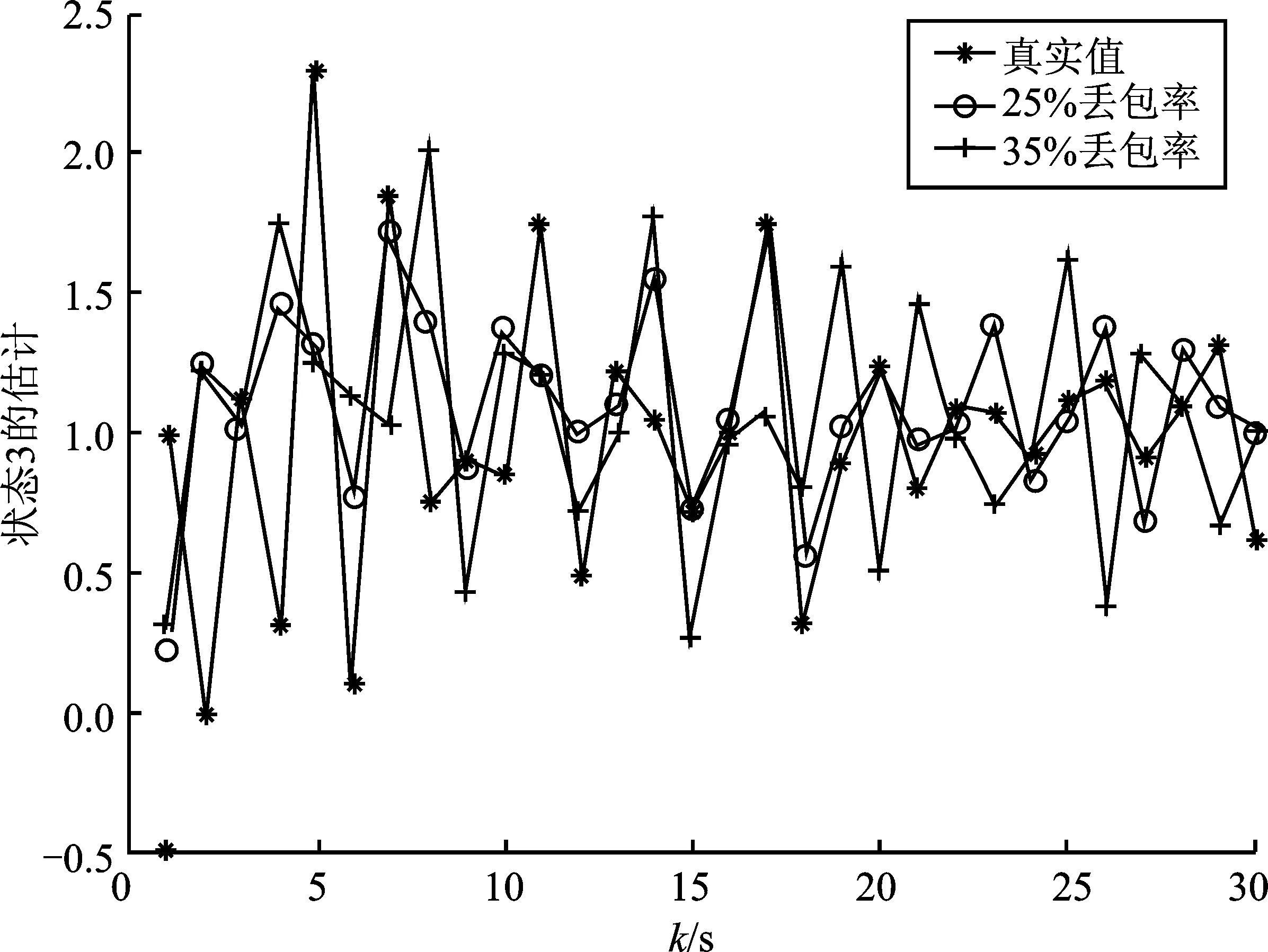
图9 x3,k的轨迹对比Figure 9.Trajectory comparison of x3,k

从图7～图9可以看出,不同的数据丢失率对滤波算法的准确性具有一定影响。随着随机变量α值增大,系统发生传感器测量值随机数据包丢失的概率变大,系统滤波器的估计性能也会变差,同时系统稳定性变差。

4 结束语

本文针对传感器测量值随机丢包的无迹卡尔曼状态估计问题,分析了在发生随机丢包时对滤波估计性能测量的影响。将收到的数据进行信息处理,运用算法补偿得到最优值,并给出了估计误差的具体计算方法,进一步分析了数据包丢失对稳定性的影响。利用MATLAB仿真软件,通过仿真实验结果总结出以下结论:1)经过算法补偿后的滤波能够较好地估计系统;2)硬件要求更高下的低丢包率对估计有更低的干扰。这一结论对于未来提升连续丢包下的系统性能具有一定的意义。

本文所提滤波算法虽然可以提高滤波器的性能,增加估计的准确性,但是也会增加滤波器的复杂度,增加计算量,故该算法还有优化空间。