基于高阶边界散射变换的二面角快速成像算法

杨俊慧 诸葛晓栋

（北京航空航天大学电子信息工程学院 微波感知与安防应用北京市重点实验室, 北京 100091）

0 引 言

毫米波与光波相比具有更长的波长，可以轻易穿透许多光学上不透明的物体，如普通的衣服材料、茂密的植被、烟雾、雾气、墙壁等.因此，毫米波成像通常被用于穿墙成像、安全检查、地面穿透雷达等.

为了对目标进行精确成像，我们通常需要高质量的图像重构算法.一系列的毫米波主动成像算法已经被提出来用于目标检测、识别和成像.后向投影(back propagation, BP)算法[1]是一种经典的时域算法，也是最常用的成像技术之一，通过建立数据域到成像域的投影并进行相干求和，可以实现最准确的成像，但存在计算量大和效率低的问题.波数域(ω-k)算法[2]通过傅里叶变换加速成像，但在频域进行的Stolt 插值会影响成像质量.距离-多普勒(range-Doppler, RD)算法[3]也需要插值，以消除由距离徙动引起的纵向和横向间的相互耦合.Chirp Scaling(CS)算法[4]无须进行插值操作，但在该算法中回波信号的距离谱会发生变化.基于以上传统成像算法，一些人体成像应用如SafeView 和QPS[5-6]在检测人体中隐藏的违禁品方面也取得了很好的效果.但它们通常面临阵列过于庞大、计算量大和成像速度慢等问题.

由于人体安检成像的最终目标是检测、提取目标轮廓并最终识别隐藏的违禁品，因此，如何快速准确地获取目标轮廓是我们重点解决的问题.边界散射变换(boundary scattering transform, BST)算法通过建立接收波前和目标形状之间的一一对应关系，可以直接从接收波前恢复目标的轮廓，而不需要一个完整的图像重构过程，极大地提升了目标检测的速度[7].SEABED (Shape Estimation Algorithm based on BST and Extraction of Directly scattered waves)[8]是一种基于边界散射变换（boundary scattering transform,BST）的实时三维成像算法，该算法通过求导操作建立了接收波前与目标轮廓间的关系，但也正因利用了接收波前的导数，该算法对误差相当敏感.在嘈杂的环境中，SEABED 获得的图像会变差.Envelope[9]使用圆的包络来建立对应关系，这种方法不利用接收波前的导数，可以对任意简单形状的目标实现稳健成像，但它需要对观测距离进行精确连接以保证成像质量.对于复杂形状的目标或多个目标，因为每个天线从目标表面的多个散射点接收多个回波，对于一个复杂的表面，这种连接往往很困难，因为每个天线观察到多个回波，有太多的候选连接.距离点徙动（range points migration，RPM）算法[10]通过对接收点到达方向(direction of arrival, DOA)的精确估计，实现了从接收点到目标点的直接映射，消除了距离连接过程，即使在复杂的边界提取中也能显著提高精度.然而，若目标表面变化尺度小于脉冲宽度，当面对复杂目标（如凹凸结构）时，该算法仍然面临由多次散射信号引起的图像失真问题.

需要注意的是，传统的基于BST 的外形重构算法往往把所有的反射当作单次反射，而对于复杂的目标，特别是凹腔目标，其内部往往存在多次反射，目标的某些部分只有多次反射信号能照射到，只考虑单次反射将导致重构目标形状的部分缺失和额外的成像伪影.

本文中，我们提出了一种基于高阶边界散射变换(high-order boundary scattering transform, HBST)的外形重构算法.与传统BST 算法中采用单站线扫描不同，我们选择了一个具有二面角结构的近场单站圆周扫描场景进行研究.通过建立正向散射模型，我们发现出射边驻定相位点所在路径的散射对回波起主要贡献，也即在二面角内的各种散射中，镜面反射起主导作用.基于此，我们在后续的推导中只考虑镜面反射对散射场的贡献，并推导了出射边的驻定相位点与回波波前之间的对应关系，并建立了可快速而精确处理二面角内多次反射回波的外形重构算法.该算法有效地消除了传统BST 算法中出现的伪影，提高了重构精度.仿真和实验结果都证明了该算法对二面角结构的有效性.

1 基本原理

1.1 二面角回波分析

为研究二面角的散射特性，我们首先对其回波进行分析，对二面角采用单站圆周扫描，将整个模型放在极坐标系下研究.如图1 所示，二面角左右对称，张角为 2φ(即左右边所在角分别为−φ和+φ)，角平分线位于0°观测角，顶点位于扫描中心圆点(0,0)，天线收发点为P0(R,θ0).设置二面角的边长L为0.3 m，圆周扫描半径R为0.7 m.由于我们只关注二面角内部的散射回波，因此将收发天线的扫描范围 θ0限制为−60° ～ 60°，扫描间隔为0.5°.

图1 单站圆周扫描几何示意图Fig.1 Schematic geometry of monostatic cylindrical scanning

基于电磁仿真软件Ansys HFSS 中的高频近似算法弹跳射线(shooting and bouncing rays, SBR)法，我们对不同张角(90°，70°，55°，40°，36°)的二面角进行仿真(频率范围为2～40 GHz)，相应的散射回波如图2 所示，回波图案显示了在不同观测角接收到的反射信号在二面角内传播的路径长度.由于二面角顶点位于扫描中心且左右对称，因此回波图案也在0°观测角附近对称.随着二面角的张角变小，散射回波中也有更高次反射出现，且同一反射次数(reflection times, RT)被接收到的观测角位置也在不断变化.二面角内出现的最大反射次数(maximum number of reflection times, MRT)和其张角的关系为[11-12]：

图2 不同张角(90°, 70°, 55°, 40°和36°)二面角的时域回波Fig.2 Time-domain echo signal of dihedrals with different opening angles (90°,70°, 55°,40° and 36°)

式中，ceil 表示向上取整.

表1 展示了常见张角内出现的MRT，由于偶次反射不能正确重构二面角边长[11]，基于圆极化波每反射一次极化方向则会改变这一规律[13-14]，使用圆极化收发器过滤偶次反射，只使用奇次反射进行目标重构.在后文中我们也仅研究二面角的奇次反射回波，不再对其偶次反射回波进行进一步分析.因此，图2 中张角为90°、70°、55°、40°、36°的二面角对应的最大奇次反射次数为1RT、3RT、3RT、5RT、5RT.其中1RT 信号所在观测角距0°最远，传播距离最短，最高次反射回波则在0°观测角附近被接收，其传播距离接近扫描半径R的两倍.

表1 常见的张角和相应的MRTTab.1 Common opening angles and corresponding MRT

1.2 驻定相位点对回波的影响

在1.1 节中我们展示了不同张角二面角的回波分布，但对二面角内的多次反射机理却仍不明了，接下来对这一问题进行研究.假设二面角为电大目标，满足高频近似条件ka≥10，其中k为波数，a为目标孔径[15-16].在此近似下，可以将电磁波的传播近似为射线传播，基于SBR 法假设除最后一次反射为全向散射外，电磁波在二面角内的反射均为镜面反射，图3为二面角内3RT 信号的传播路径示意图.基于镜像反射原理，我们可以求出2n−1次反射的镜像反射点P′(R,θ2n−1)，其中镜像反射点P′的角度为

图3 二面角内三次反射回波的传播路径示意图Fig.3 Schematic of the propagation path of triple reflections within the dihedral

需要注意的是， θ为首次入射边的角度.由于在P0点发射的电磁波在二面角内反射后到达最终的出射点P所走的路径长度与2n−1次镜像反射点P′到P的路径长度相同，因此可以求出该段路径长度为

同时，可以求出出射点P到接收点P0的距离：

因此，根据总传播距离Rall=d1+d2可以建立接收场的表达式：

也即在某一观测点P0(R,θ0)接收到的散射回波为多条传播路径在出射边上各点的散射回波之和.如图4 所示，出射边上每个点P(r,θ)均向接收点P0(R,θ0)散射回波，回波传播路径d=|PP′|+|PP0|.根据式(5)中的接收场表达式可以得到图4 所示的回波.需要注意的是，当收发点位于大观测角度时(|θ0|＞φ)，由于遮挡效应，可能存在接收点无法接收到部分边散射回波的情况.如图5 所示，由于左侧边遮挡，此时只能接收到(rmin,L)区域的散射回波，其中 θ表示出射点所在边的角度(由于本文仅讨论奇次反射，因此和入射点所在边的角度相同)；当|θ0|＞φ时，rmin为观测点P0与遮挡边端点P1的连线和出射点所在边OP3的交点P2到原点O的长度，可以表示为

图4 右侧边出射的散射波在二面角内的等效传播路径Fig.4 Schematic of the equivalent propagation path of the scattered wave emitted from the right side of the dihedral

图5 二面角的遮挡效应示意图Fig.5 Schematic of the shading effect of the dihedral

但在实际散射中，图4 中各条路径的散射回波对总接收场的贡献并不相同.根据驻定相位原理[17]，我们对式(5)中的指数项求导：

可求得对式(5)中接收场积分贡献最大的点(驻定相位点)，也即在观测角 θ0接收到的散射回波中贡献最大的散射点在出射边的位置r：

不难求证，该散射点所对应传播路径在二面角内均按照镜面反射来传播[18].

图6（a）和图7(a)分别展示了在70°二面角右侧边出射的1RT 和3RT 回波信号图，在两条白虚线之间的观测角内存在强回波信号；图6（b）和图7 (b)展示了在不同观测角下各出射点r∈(0,L)所在路径相应的距离分布图，其中强度表示距离信息.图中红色点为根据公式(8)求出的各观测角下驻定相位点的位置，由于在大部分观测角下驻定相位点都不在出射边上(也即r∉(0,L)，此时L=0.3 m)，因此只有白色虚线附近才出现驻定相位点.这意味着当驻定相位点位于出射边上时，在该观测角下能接收到强散射回波，这也侧面说明在所有出射点中，驻定相位点对回波贡献最大.需要注意的是，虽然在图6 (b)中左边虚线附近的观测角度下也存在驻定相位点，但此时由于左侧边的遮挡，在这些观测角下并不能接收到散射回波.

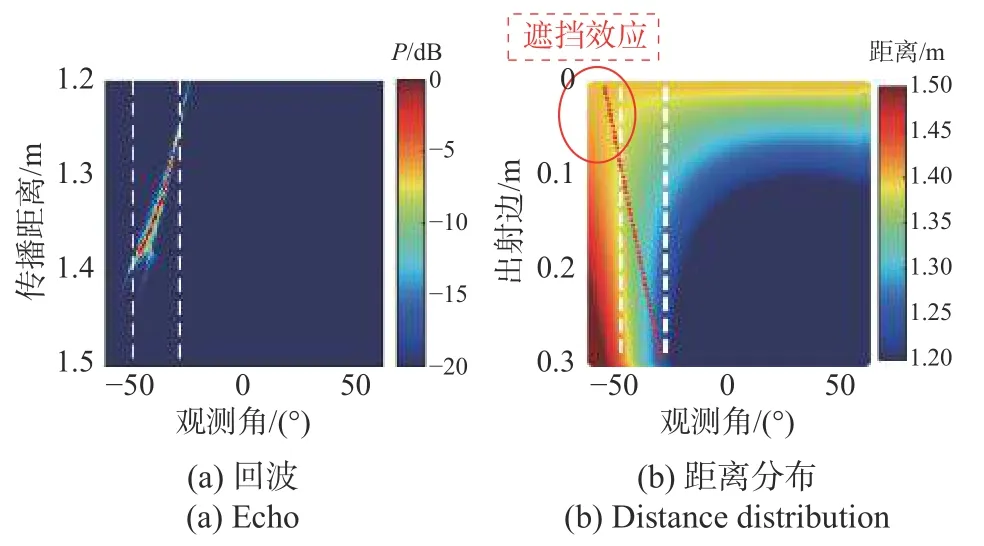
图6 70°二面角右侧边出射的1RT 信号的回波和不同观测角下各出射点所在路径的距离分布Fig.6 Echo and distance distribution of the path of all exit points under different observation angles (of 1RT signal emitted from the right side of a 70° dihedral)

图7 70°二面角右侧边出射的3RT 信号的回波和不同观测角下各出射点所在路径的距离分布Fig.7 Echo and distance distribution of the path of all exit points under different observation angles (of 3RT signal emitted from the right side of a 70° dihedral)

我们将公式(8)代入公式(3)和公式(4)，可以求出驻定相位点所在路径的总传播距离为

同时，根据式(8)可以推导出观测角 θ0和驻定相位点位置r的关系：

根据r∈(rmin,L)这一条件可以求出 θ0的范围，再结合式(9)和式(10)即可求出各观测角 θ0下驻定相位点所在路径的总传播距离Rall.如图8 所示，我们给出了90°、70°和40°二面角驻定相位点所在路径的总传播距离Rall和观测角 θ0之间的关系，其中黄色虚线由公式（9）得到，由于只在某些观测角度能接收到相应回波，因此有效区域如黑色实线所示.可以看出，该曲线与图2中相应二面角回波波前位置的一致性，因此可以通过驻定相位点所在路径的传播距离表示回波波前.

图8 在各观测角下不同张角二面角出射点驻定相位点所在路径的总传播距离Fig.8 Total propagation distance of the path where the stationary phase point stands of different opening angles of the dihedral at each observation angle

1.3 HBST 算法

从1.2 节可知，驻定相位点所在的全镜面反射路径对回波贡献最大，因此只考虑镜面反射对回波的贡献，并基于此建立驻定相位点(r,θ)与回波波前点(Rall,θ0)间的一一对应关系.镜面反射路径的传播规律为最终垂直入射二面角边后沿原路返回[18]，图9(a)～(c)分别对应二面角内1RT、3RT、5RT 的传播路径，同时也展示了各次反射中的极限情况，红色实线表示各次反射能照射到的区域，紫色实线表示能接收到相应反射信号的角度范围.

图9 二面角内一、三、五次反射的传播路径和极限情况Fig.9 Propagation paths and the limit cases of 1RT, 3RT and 5RT within the dihedral

不难发现，随着反射次数增加，电磁波在二面角内能照射到的区域也越来越广，最高次反射能照射到二面角内所有区域.理论上可以通过最高次反射回波重构二面角外形，但由于二面角存在缺口时仅用最高次反射无法完整重构目标，因此在我们的算法中所有反射回波均会被用来进行重构.

由于电磁波在二面角内最终垂直入射后沿原路返回，故图3 中的观测点P0、出射点P和镜像反射点P′在一条直线上，如图10 所示.因此，电磁波由观测点P0出射并在二面角内反射后再回到观测点P0的总传播距离Rall等效于观测点P0到镜像反射点P′的距离|P0P′|，其中等效反射点Pe位于|P0P′|中点，也即|P0Pe|=Rall/2，观测点P0发射的电磁波到等效反射点Pe的往返距离等于真实传播距离Rall.若将该2n−1次反射当作一次反射处理，则重构点位于等效反射点Pe(re,θe)处.当n=1时，如图10(a)所示，等效反射点Pe与驻定相位点P重合；当n＞1时，如图10(b)所示，等效反射点Pe位于驻定相位点P外侧，其中驻定相位点P所在角度θ 与等效反射点Pe所在角度θe的关系为：θ=θe/(2n−1)，此时若将2n−1次反射当作一次反射处理，则重构点位于角度 θe上，在二面角外侧出现成像伪影.

图10 一次反射和高次反射路径中等效反射点和驻相点的关系Fig.10 Relationship between equivalent reflection points and standing phase points in 1RT and high-order RT paths

根据|θe−θ0|=∠PeOP0，我们可以求出驻定相位点P(r,θ)所在角度：

根据式(8)和式(11)，我们可以建立由回波波前点(RAB,θ0)到驻定相位点(r,θ)的重构关系，即针对多次反射回波信号的HBST 算法.当处理2n−1次反射回波信号时，将式(11)中的分母设置为相应的2n−1，即可得到正确的目标角度.此外，根据电磁波在二面角内的反射路径可知，驻定相位点(r,θ)可以视为2n−1次反射中的首次反射点r1和第2n−1次反射点r2n−1，通过以下公式可以不断迭代求出其他反射点：

1.4 算法应用流程

基于式(11)可知，为了正确进行外形重构，有必要区分不同反射次数和不同入射方向上的波前点(Rall,θ0).然而，若二面角内的m1RT信号由正确入射方向的m2RT算法(即式(11)中分母取为m2)处理，那么处理后的单边角θ′=m1/m2·θ.当m1≠m2时, θ′仍为常数但不等于正确角度 θ.然而，如果将首先入射到二面角右侧边或左侧边的信号视为首先入射到左侧边或右侧边的信号，则会出现角度偏差|θ −θ′|=2ψ/(2n−1).由于 ψ不是一个常数，所以 θ′的值也是变化的.在此基础上，我们提出一种方法，以避免手动划分属于不同RTs 和入射方向的波前，从而实现成像的自动化.

对于MRT=2nmax−1的波前，我们可以通过各次反射算法(即式(11)分母中n=1,...,nmax)来分别处理所有回波波前点，同时不区分入射方向，得到nmax组结果.通过设置一个适当的角度阈值，保留在所有nmax组结果中均存在的角度范围对应的点，舍弃其他的点，可以根据所有保留点的位置(r,θ)来重构目标形状.

图11(a)和(b)显示了不区分入射方向，使用1RT 和3RT 算法对接收到的60°二面角回波波前点(Rall,θ0)进行重构的重构点云图.由于在60°二面角中存在1RT 和3RT 回波，因此当采用正确入射方向的重构算法时会出现恒定的重构角(图11(a)中的60°和180°角以及图11(b)中的20°和60°角)，表2 解释了这些角度的对应关系，而其他非恒定角度的重构点则是由错误入射方向算法处理得到的.保留用1RT 和3RT 算法处理得到的两组结果中都包含的角度范围的点(也即图11(a)～(b)中黑色虚线覆盖的点)，舍弃其他的点，则可以得到最终的重构目标形状，如图11(c)所示.需要注意的是，由于BST 算法是基于点之间的关系，我们通常使用点云图来表示接收到的波前和重构目标的形状.传统的BST 算法中所有的重构点都用黑色点表示，因此无法判断散射强度，这里我们用不同颜色的点来表示相应区域的功率强度.

表2 用m2RT算法处理60°二面角m1RT波前时重构目标的开口角度（正确入射方向）Tab.2 Reconstructed opening angle of 60° dihedral when processing the m1RT wavefront with m2RT algorithm in correct incidence direction

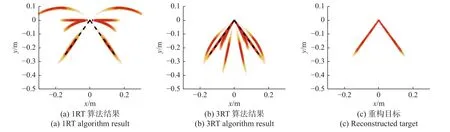
图11 用HBST 算法处理60°二面角的波前点得到的点云重构结果Fig.11 The point cloud reconstruction results obtained by processing extracted wavefront points of 60° dihedral with HBST algorithm

图12 为HBST 算法的流程图，图13 为对该算法的图例说明.HBST 算法具体流程下：

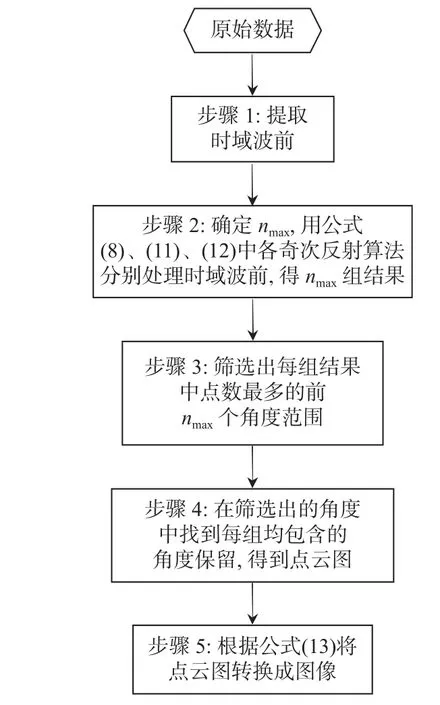
图12 基于HBST 的重构算法流程图Fig.12 Flowchart of the proposed HBST based reconstruction algorithm

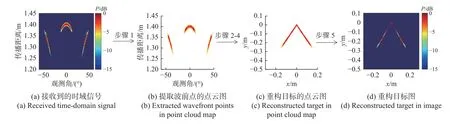
图13 基于HBST 的重构算法示意图Fig.13 Illustration of the proposed HBST based reconstruction algorithm

1)选择合适的功率阈值，并获得功率大于该阈值的强散射回波的波前点信息(功率值、观测角 θ0和传播距离Rall).

图13(a)为60°二面角的反射回波，图13(b)则是从图13(a)中提取的波前点的点云图，其中点的颜色越深，对应的功率值越大.图13(a)是一幅图像，图13(b)是所有提取的波前点的集合.

2)人为地确定nmax.首先用传统的BST 算法重构目标，重构结果中最小的张角就是目标的真实角度2φ.根据公式(1)求出MRT，再根据nmax=ceil(MRT/2)确定nmax，然后用各(2n−1)RT (n∈[1,nmax])算法分别处理波前点.如果重构点 (r,θ)由同一RT 算法进行处理，不区分入射方向，将其视为一组数据，则能得到nmax组结果.

3)每组结果中都有许多角度，筛选出每组结果中点数最多的前nmax个角度范围.由于用正确的入射方向处理所得到的角度是恒定的，所以这些角度的点的数量最多.例如，图11(a)中角度为60°和180°、图11(b)中角度为20°和60°的点最多.需要注意的是，在处理过程中，实际角度和理论角度之间存在一定的偏差，因此我们需要设置角度阈值(例如1°)来限制角度范围.此外，在某一组结果中，对应正确角度的重构点的数量不一定是最多的，因此不能假设包含最多的点的角度是目标角度，它可能是nmax个恒定角度中的任何一个.因此须找到每组结果中点数最多的前nmax个角度范围.通过这种方式，可以在nmax组结果中得到nmax·nmax个角度范围，然后计算每个角度范围的平均值，以便在下一步中更好地进行比较.

4)根据获得的nmax·nmax个角度平均值，找到所有nmax组结果中均存在的目标角度.可以通过在点云图中保留目标角度下的点而放弃其他点来获得目标形状，如图13(c)所示.

5）根据所选点的信息，可以通过式(13)将点云图转换成图像，计算出图像中每个像素的平均功率值Pij即为图像中每个像素点的强度：

式中：(i,j)为该像素点在图像中的位置；n为像素点(i,j)中包含的重构点数量；Pt为每个重构点的功率.

2 仿真和实验结果

我们使用与图2 相同的扫描结构和频率，并采用BP 算法、传统的BST 算法和本文提出的基于HBST 的重构算法分别对张角为70°、 55°和45°二面角进行重构，结果如图14 (a)～(c)所示.此时重构二面角的张角分别为69.56°、54.98°、45.04°，可见重构角度具有较小的误差.

图14 不同张角二面角的仿真重构结果Fig.14 Simulation reconstruction results of dihedrals with different opening angles

由于在张角小于90°时高阶反射出现，此时BP 算法和传统的BST 算法成像结果中出现重构伪影，只有二面角的外边沿被正确重构.对于张角为70°、55°和45°的二面角进行重构，分别出现了210°、165°和135°的伪影，这是因为3RT 被当作1RT 处理.

利用HBST 算法、BP 算法、BST 算法和文献[11]中算法分别对45°和70°二面角进行成像，并计算每种成像结果的相对平均误差(relative mean error,RME)和计算时间，结果如表3 所示.所有四种算法都是用MATAB 代码实现的，并在一台装有英特尔i5-8300H 中央处理器(CPU)@2.3 GHz 和24 GB 随机存取存储器(random-access memory, RAM)的计算机上运行.其中RME 表示成像结果与基准图像相比的相对误差，其定义如下：

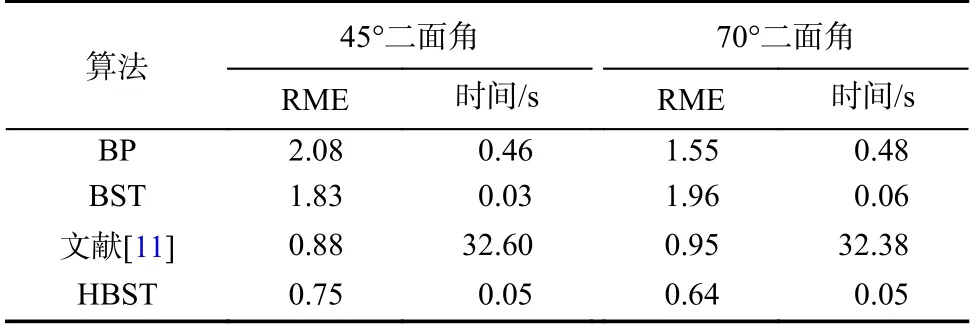
表3 不同算法准确度和计算时间的比较Tab.3 Comparison of accuracy and calculation time of different algorithms

式中：N为成像区像素点的个数；和分别为基准图像和目标图像中第j个像素点的逻辑值，当像素点的功率值大于阈值功率时，其逻辑值为1，反之为0.RME 越小，说明目标图像与基准图像越相似，即相应的成像算法的精度越高.

从表3 可以看出，由于考虑了多次反射，文献[11]中的算法与BP 和BST 算法相比具有更高的成像精度，但文献[11]中的算法需要更长的计算时间，而HBST 算法由于计算量较小，所以速度更快.同时，当选择合适的阈值时，由于HBST 算法建立了目标回波波前与目标外形间的一一映射关系，因此目标存在的区域对应高反射率，没有目标的区域反射率为0.而文献[11]则是将回波信号向目标空间投影，并通过相干叠加来重构目标反射率分布，目标所在位置反射率高，但没有目标的位置反射率值虽然相对较小，但却并不为0.因此在此情况下本文算法有更高的精度.

我们用实验数据对HBST 算法进行进一步验证.在暗室中进行近场圆周扫描实验，在矢量网络分析仪的端口上连接一个喇叭天线作为发射和接收天线.将一个电机连接到转盘上，控制机械转盘的旋转.同时将一个低反射率的泡沫台放置在转盘上，并在转盘上放置要测量的目标.电机和矢量网络分析仪均由计算机控制.此外，实验频率范围为4～20 GHz，频率步长为0.02 GHz.

如图15(a)所示，测试了由多个二面角结构组成的复杂形状的目标.对目标的下半部分(图16(a) 中红线标记部分)进行180°圆周扫描，扫描半径约为0.7 m；图15(b)显示了目标的下半部分的轮廓，中间60°二面角的边长为0.09 m，而外侧两边边长为0.07 m.使用不同的算法对目标进行重构，结果如图16 所示.结果显示：BP 和BST 算法将3RT 视为1RT，存在180°伪影；相比之下，本文基于HBST 的算法可以准确地重构目标形状.

图15 复杂目标示意图Fig.15 Schematic diagram of complex target

图16 使用不同算法对复杂目标底部进行重构的实验结果Fig.16 Experimental reconstruction results of the bottom part of the complex-shaped target using different algorithms

3 结 论

本文研究了不同张角二面角的回波分布规律，同时发现镜面反射回波在所有散射回波中的贡献最大.基于此，我们仅考虑镜面反射回波对散射场的贡献，建立了反射回波波前与目标轮廓之间的一一对应关系，提出了能够处理二面角内多次反射的HBST 算法，实现了二面角的快速成像.但该方法的问题在于对回波波前的提取精度要求较高，通常要求距离分辨率小于1 cm.这是由于波前位置的微小误差将导致重构点位置的较大偏差，尤其是当最高次反射波前存在偏移时.因此该方法希望成像带宽尽可能大(大于15 GHz)，以便有更精细的距离分辨率来获得更精确的波前位置.同时，由于目前的算法主要针对二面角或者多个二面角的组合目标，且当二面角表面较粗糙时(如存在凹陷或凸起)，该算法的重构结果将恶化.因此我们下一步的工作将提升该算法的普适性，以应用于其他存在多次反射的复杂目标.