典型角反阵列双基地一维距离像特性
张文明 邱梦奇 艾小锋 胡旖航 赵锋
(国防科技大学 电子信息系统复杂电磁环境效应国家重点实验室, 长沙 410073)
0 引 言
角反射器在海战场应用广泛,角反射器及其构成阵列的散射特性备受关注.文献[1]分析了浮空式角反射器及其阵列雷达散射截面积(radar cross section, RCS)模型的统计特征.文献[2]对新型二十面体三角形角反射器全角域静态RCS 进行仿真,并利用三种分布模型进行统计建模,取得了较好的拟合效果.文献[3-4]对几种典型的角反射器电磁散射特性进行了建模仿真,并分析了海战场环境下角反射器的干扰效果.文献[5]分析了典型角反射器的极化旋转域特性差异,研究了全方位角度下角反射器的极化旋转域特性变化规律.上述研究主要针对单基地雷达,实际情况中现有单基地雷达难以对抗角反射器干扰,若采用双基地雷达来观测,收发分置的几何构型可能导致观测的RCS 特性产生较大差异.
双基地雷达是近年来雷达界的研究热点,但对角反射器双基地散射特性的研究还不充分.文献[6]分析了不同张角二面角的双基地散射特性及其合成孔径雷达(synthetic aperture radar,SAR)图像表现形式,研究了双基地角对角反射器双基地RCS 的影响.文献[7]研究了三面体角反射器的双基地RCS 特性,指出双基地角越大,RCS 峰值下降越快.文献[8-10]分析了三面角、八面角和二十面角单/双基地RCS 理论模型.文献[11]通过电磁计算和暗室测量对比了角反射器单双基地RCS 分布特性,指出角反射器双基地RCS 在较大范围内小于单基地RCS.但是对角反阵列的双基地一维距离像特性还有待进一步分析.
相比于窄带雷达,宽带雷达具有更高的距离分辨率,对于舰船、角反射器等电大尺寸海上目标,使用宽带雷达可获取目标的精细结构信息.因此,本文选择典型八面体角反射器,通过电磁计算和暗室测量对角反射器阵列单/双基地一维距离像特性进行了对比分析,总结了其随观测角度的变化规律,为宽带双基地雷达抗角反射器干扰的可行性提供了理论支撑.
1 典型角反射器阵列观测与电磁计算建模
本文使用八个三角形角反射器组合成具有对称结构的双棱锥八面体角反射器,如图1(a)所示,以角反质心为坐标原点,x轴为∠AOB的角平分线,z轴沿着双棱锥轴线方向,与x、y轴组成右手直角坐标系.方位角定义为在xOy平面内顺时针方向转到x轴的角度,用φ表示,取值范围为0°~360°.俯仰角定义为与z轴的夹角,用θ 表示,取值为0°~180°.八面体角反射器的直角边长为a.θT、φT分别为入射视线俯仰和方位角,θR、φR分别为接收视线俯仰和方位角.
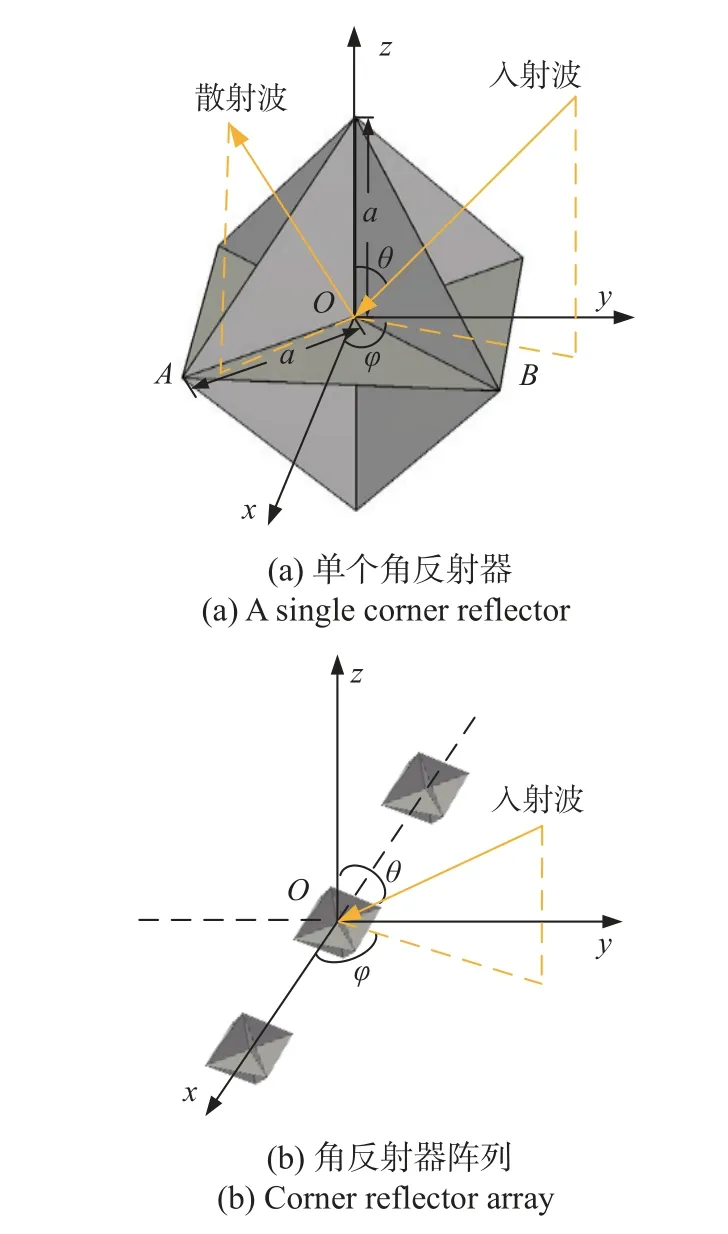
图1 单个角反射器和角反射器阵列仿真示意图Fig.1 Simulation schematic of a single corner reflector and corner reflector array
对于角反射器阵列,采用3 个相同尺寸的八面体角反射器组合成对称结构,如图1(b)所示,以中间角反射器的质心为坐标原点,坐标系的建立同单个角反射器电磁仿真坐标系,3 个相同尺寸、相同方向的八面体角反射器均匀放置在x轴上.
双基地角的计算方法如下:
电磁波入射方向矢量为
电磁波接收方向矢量为
双基地角 β为电磁波入射方向Ei与接收方向Es的夹角,因此满足下式
电磁仿真参数设置如表1 所示.

表1 角反射器阵列电磁仿真参数设置Tab.1 Parameter settings for electromagnetic simulation of corner reflector array
2 角反射器阵列双基地一维距离像特性
当雷达距离分辨率较高时,舰船等效为扩展目标,单个角反射器不足以形成有效干扰,须将多个角反射器以一定的间距排列成角反射器阵列,与舰船扩展目标形成相似的一维距离像.下面研究角反射器阵列宽带双基地散射特性,对单/双基地角反射器阵列一维距离像特性进行比较.
图2 为俯仰角为30°、方位角为0°~360°时的八面体角反射器阵列一维距离像分布图,为了便于观察不同角度下角反射器阵列一维距离像的长度,对一维距离像幅度值取了对数.
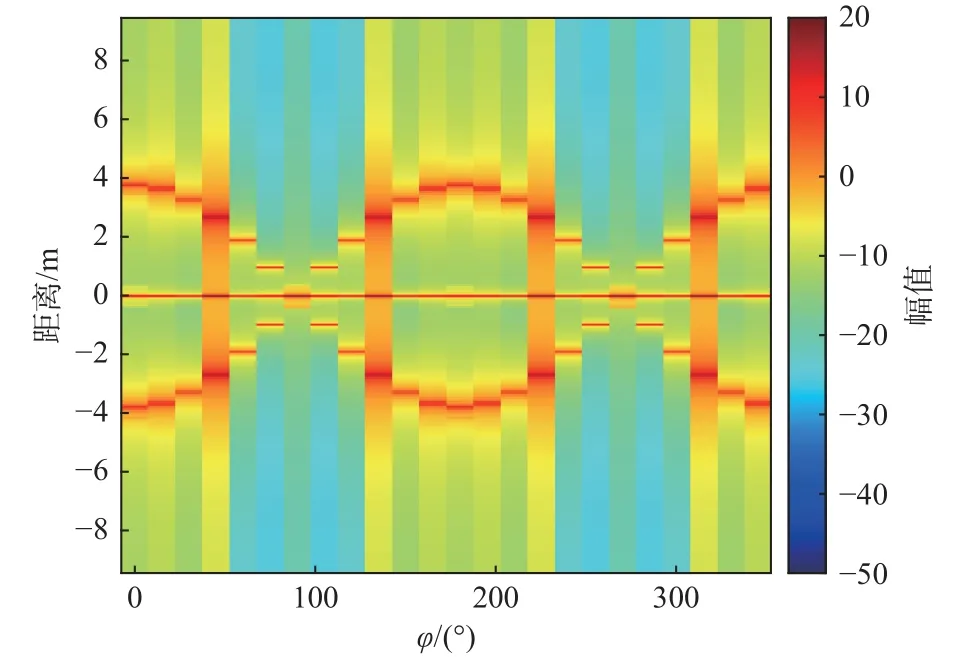
图2 角反射器阵列单基地一维距离像分布图(θ=30°)Fig.2 1D HRRP profile of corner reflector array for monostatic radar (θ=30°)
从图2 仿真结果可以看出,单基地模式下,由3 个八面体角反射器组成的均匀阵列一维距离像分布随着方位角的改变而规律变化.当方位角为90°、270°时,角反射器阵列轴线与电磁波方向垂直,构成镜面反射,一维距离像为一个强散射中心,而在其他方位角,均可观察到3 个清晰的散射中心.
对于角反射器阵列双基地一维距离像分布,选取入射俯仰角为30°,入射方位角分别为0°、45°的情况进行分析,仿真结果如图3、图4 所示.当入射俯仰角为30°,入射方位角为0°,接收俯仰角为30°、60°时目标一维距离像随着接收方位角的分布如图3(a)、(b)所示;当入射俯仰角为30°,入射方位角为45°,接收俯仰角为30°、60°时目标一维距离像随接收方位角的分布如图4(a)、(b)所示.
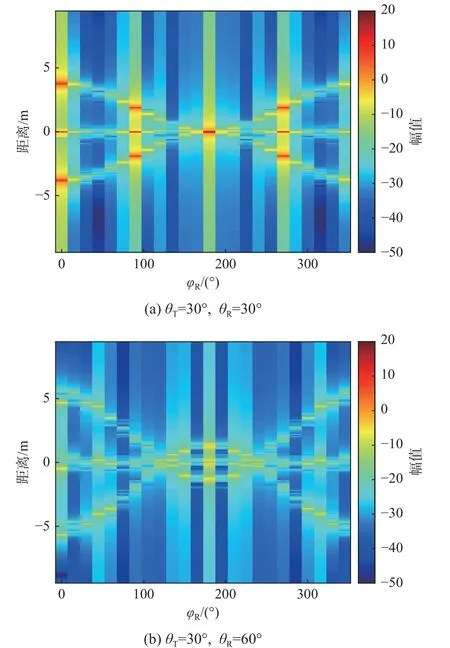
图3 角反射器阵列双基地一维距离像分布图( φT=0°)Fig.3 1D HRRP profile of corner reflector array for bistatic radar( φT=0°)
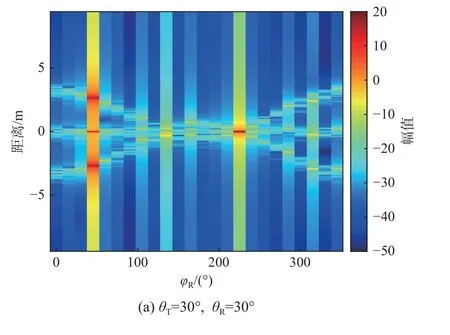
图4 角反射器阵列双基地一维距离像分布图( φT=45°)Fig.4 1D HRRP profile of corner reflector array for bistatic radar ( φT=45°)
从图3 仿真结果可以看出,双基地模式下,当入射方位角为0°时,角反射器阵列一维距离像长度和强散射点的分布随着接收方位角变化关于180°方位角对称.对于图3(a),即入射和接收俯仰角相同时,由于此时双基地角平分线与z轴平行,在接收方位角为180°时出现强散射中心,此外,在接收方位角为0°、90°、270°、360°时,距离像峰值明显,与文献[11]中入射方位角为0°时角反射器的RCS 空域分布特性相同.对于图3(b),即入射和接收俯仰角不同时,一维距离像峰值幅度大幅下降,相差约30 dB,无极大的峰值.
保持电磁波入射方向的俯仰角不变,当改变入射方位角为45°时,角反射器阵列一维距离像的分布如图4(a)所示,当接收方位角为45°时,入射方向与接收方向相同,出现强散射中心;当接收方位角为225°时,由于双基地角平分线垂直于角反阵列轴线,也出现强散射中心.一维距离像幅值分布与文献[11]中入射方位角为45°时角反射器阵列的RCS 空域分布特性相同.对于图4(b),入射和接收俯仰角不同时,一维距离像峰值幅度大幅下降,相差约30 dB,无极大的峰值.
角反射器阵列双基地一维距离像,其幅值分布与角反射器阵列RCS 空域分布规律一致,随着接收方位角的变化而起伏明显.双基地一维距离像所在区域变化具有明显规律性,强散射点分布对称.一维距离像幅值随接收方位角起伏规律与角反射器阵列中角反射器数量和接收方位角的改变有关,接收方位角变化时,一维距离像幅值总体变化趋势一致,但极大峰值的个数和位置不同.当入射俯仰角与接收俯仰角相等时,会在构成镜面反射的角度出现极大峰值,而俯仰角不同时不会出现极大峰值.
为了定量评估角反射器阵列单/双基地一维距离像相似度,使用余弦相似度法来求解,公式如下:
式中:i表示某方位角;xi和yi分别表示该方位角得到的角反射器阵列的单/双基地一维距离像,对其进行余弦相似度求解并进行归一化,得到结果如图5 所示.
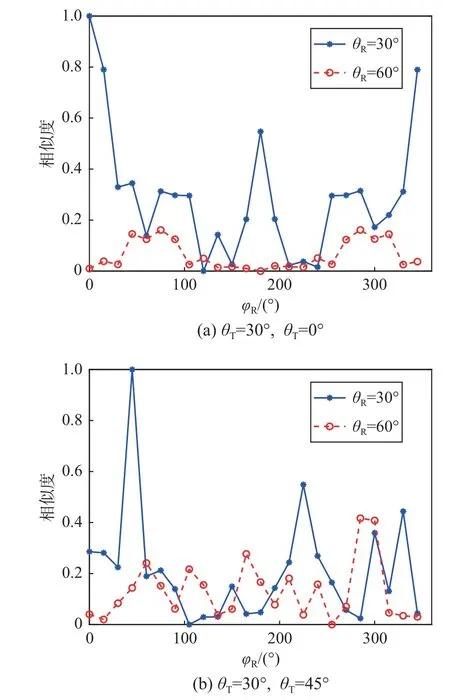
图5 角反射器阵列单/双基地一维距离像相似度Fig.5 Similarity of monostatic and bistatic 1D HRRP profiles for corner reflector array
图5 中相似度为1 时为单基地方向;随着双基地接收方位角的变化而迅速降低,只有在相同俯角条件下对称的方向会出现较强的相关性;其余位置相似度小于0.4;特别是入射和接收俯仰角不同时,相似度多小于0.2.当入射方向不同时,对入射方向的单基地一维距离像峰值与该入射方向下不同接收方位角的双基地一维距离像峰值比值进行统计,结果如表2 所示.

表2 角反射器阵列单/双基地一维距离像峰值比值Tab.2 Peak ratio of monostatic and bistatic 1D HRRP profiles for corner reflector array
根据统计结果可知,角反射器阵列单/双基地一维距离像峰值比均值相差达到30 dB,角反射器阵列宽带双基地散射强度与单基地散射强度存在明显差异.
3 暗室测量验证与分析
在微波暗室中,采用矢量网络分析仪测量角反射器的散射特性数据,暗室测量参数设置如表3 所示.对扫频的散射测量结果进行背景抑制、逆傅里叶变换等处理,利用汉明窗对目标所在区域进行加窗,得到一维距离像.实验测量场景如图6 所示,固定发射天线位置,通过转动接收天线,改变发射天线与接收天线相对于转台的夹角,从而改变收发天线相对于目标的双基地角,对不同双基地角下角反射器阵列的散射特性进行测量.测量的角反尺寸为0.15 m,天线测量距离大于1.5 m,因此当使用10 GHz 频率电磁波时,对于每一个角反均满足远场条件.单基地模式时,发射天线与接收天线位于同一位置,夹角为0°,两天线同时逆时针转动,改变天线方位角从−22.5°到22.5°,得到角反阵列单基地一维距离像如图7 所示.从图7 可以清楚看到每个角反射器对应的峰值,由于观测角度比较低,远端的角反射器被遮挡,所以强度较弱.双基地模式时,固定发射天线方位角为−22.5°,通过逆时针转动接收天线,改变两天线夹角从0°到90°,即改变双基地角从0°到45°,进行角反射器阵列双基地散射特性测量,并对实验测量数据进行分析,得到角反阵列双基地一维距离像如图8 所示.对图8 中角反射器阵列双基地一维距离像序列进行进一步分析,取双基地角分别为0°、22°、45°时的一维距离像如图9 所示.
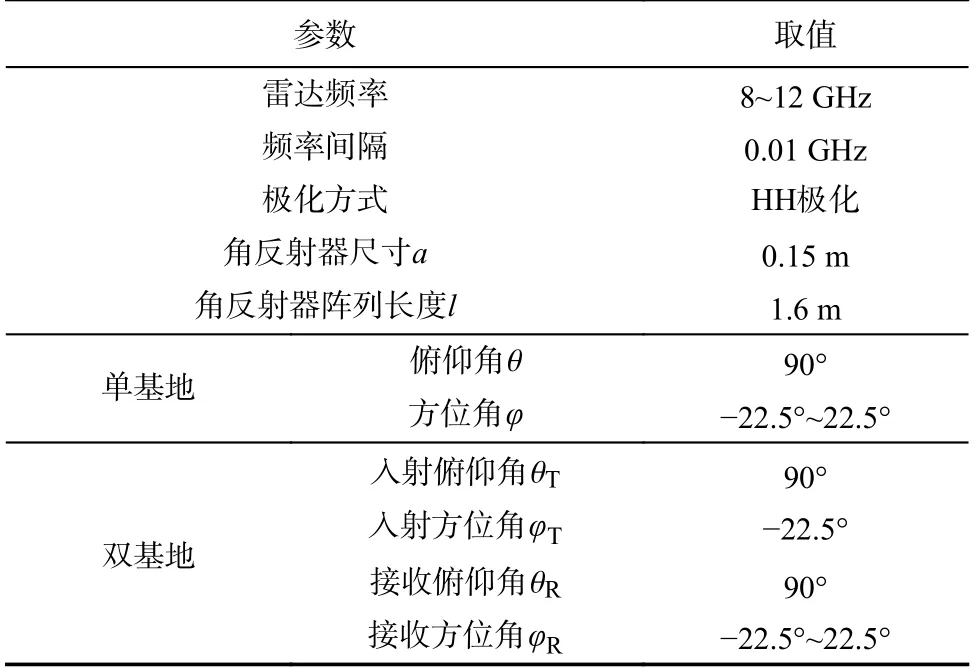
表3 角反射器阵列实验测量参数设置Tab.3 Setting of experimental measurement parameters for corner reflector array

图6 角反射器阵列暗室测量实验图Fig.6 Corner reflector array darkroom measurement experimental picture
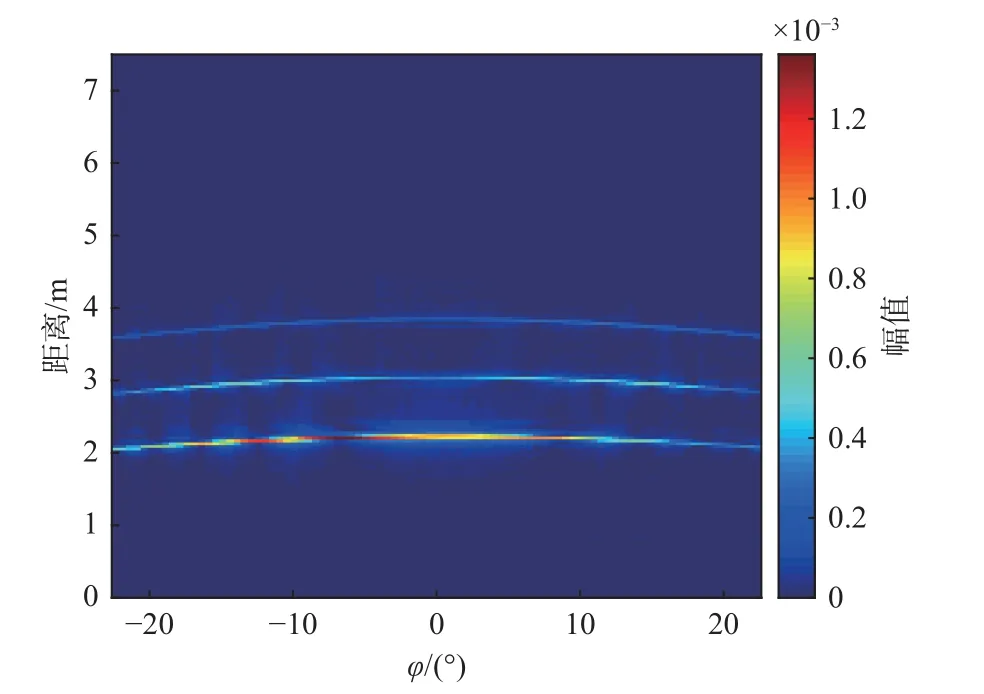
图7 角反射器阵列单基地一维距离像Fig.7 1D HRRP of corner reflector array for monostatic radar
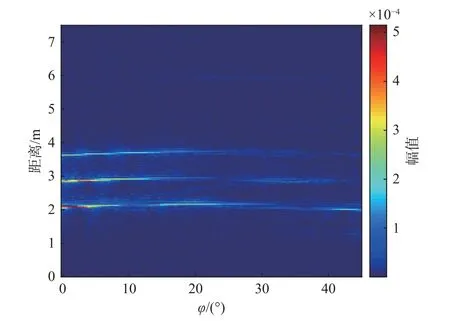
图8 角反射器阵列双基地一维距离像Fig.8 1D HRRP of corner reflector array for bistatic radar
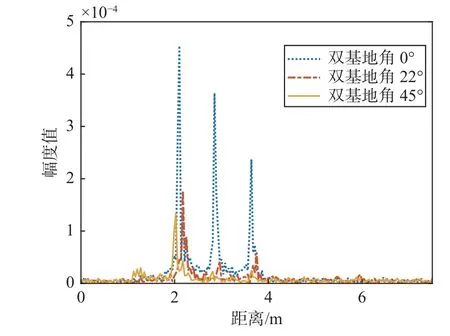
图9 角反射器阵列特定方位双基地一维距离像Fig.9 1D HRRP of corner reflector array for specific azimuth bistatic radar
对于图9,双基地模式下,角反射器阵列中3 个角反射器分别对应着一维距离像中的3 个峰值,峰值的位置如表4 所示.可以看出:随着双基地角不断增大,角反射器阵列一维距离像长度逐渐增大.
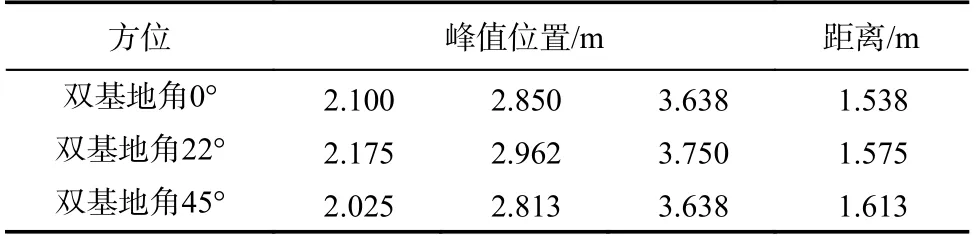
表4 角反射器阵列双基地一维距离像长度Tab.4 HRRP length of corner reflector array for bistatic radar
由图9 观察到:由于3 个角反射器位于同一水平面,存在遮挡效果,阵列中第一个角反射器的散射强度依次大于后面两个;当双基地角为0°时,即单基地方向,一维距离像幅度值明显大于双基地.由表4 可知:双基地模式下,随着接收天线方位角的变化,即双基地角逐渐增大,角反阵列一维距离像长度不断增大;当双基地角为45°时,一维距离像长度最长,此时,角反阵列轴线与双基地角平分线平行.
通过对比图7 和图8 观察到:随着方位角的变化,角反射器阵列单基地一维距离像的幅值起伏不大;而随着双基地角的增大,角反射器阵列双基地一维距离像的幅值不断减小,与文献[11]中角反射器阵列单/双基地RCS 空域分布特性的结果一致,且在一定范围内,角反射器阵列双基地散射强度小于单基地.
综合电磁计算和暗室测量结果,可以发现由于角反射器的结构高度对称,角反射器阵列双基地一维距离像存在明显的方向性,单/双基地一维距离像差异较大,而复杂目标单/双基地一维距离像差异较小,因此使用双基地雷达抗角反射器干扰具有一定可行性.即采用T/R-R 复合双基地雷达联合观测对目标区域成像,可同时得到目标区域的单/双基地一维距离像,当两个雷达飞行高度不同且相对于目标区域构成一个大于30°的双基地角时,对T/R 和R 站观测到的一维距离像进行比较,利用这个差异可以判断目标是否为角反射器假目标.
4 结 论
本文通过电磁计算和暗室测量研究了角反阵列的单/双基地一维距离像特性,分析发现角反阵列的单基地一维距离像的幅度在各个方向都很强,而双基地一维距离像的幅度随着观测方位角的增加逐渐减弱,甚至下降几十分贝,只在特殊的镜面反射区和前向散射区出现较强的一维距离像,这一特性可用分布式协同观测合理部署几何构型,从而有效剔除角反阵列干扰.值得注意的是,本文目前计算和测量的散射特性均是角反射器静止状态下的,实际中角反射器会随着风和海浪摆动,因此其相对于雷达视线的角度也会变化,导致角反射器散射特性剧烈起伏,这种动态特性需要深入研究.下一步将结合角反阵列运动模型开展动态特性研究并量化对比分析舰船和角反阵列的单/双基地一维距离像差异,为角反射器识别提出定量判别依据.

