一种不对称级联H桥多电平逆变器通用的线性功率均衡方案
叶满园, 陈子豪, 彭瑞凡, 刘文芳
(华东交通大学 电气与自动化工程学院,江西 南昌 330013)
0 引 言
多电平逆变器(multilevel inverters,MLIs)具有低电压应力、低的总谐波失真(total harmonic distortion,THD)以及低电磁干扰等优点,因此在中压大功率系统中是应用最多的类型之一,例如多电平逆变电机驱动器、电动汽车充电站、光伏并网逆变器、不间断电源等[1-3]。
电容悬浮式、二极管箝位式以及级联H桥(cascaded H-bridge, CHB)逆变器是MLIs中最为经典的3种拓扑结构[4-6],其中电容悬浮式和二极管箝位式逆变器无需器件串联就可以应用在具有一定电压等级的传动系统中,但这些拓扑在使用时电容电压的控制存在着一定的难度,CHB逆变器不像前两者存在电容电压控制问题,而且具有易于模块化的优点,但CHB逆变器需要多个隔离的直流电源[7]。因此不对称级联H桥(asymmetric cascaded H-bridge,ACHB)多电平逆变器被提出用于改善这个缺点[8-9],ACHB多电平逆变器的功率单元由不同电压的直流电源供电,能够在逆变器输出电压电平数目一定时,使用更少的H桥单元,从而达到减少直流侧隔离电源的目的[10-12]。文献[10]采用直流侧电源电压比为1∶4∶16的三相不对称多电平逆变器拓扑结构,逆变器的线电压最高能输出85个电平,并且能够在输出电压波形保持较低的谐波含量的情况下,以较低的频率下运行来减少损耗。文献[11]提出一种新的E型模块结构的不对称型多电平逆变器。每个模块产生13个电平,与同类拓扑相比,该结构的设计具有开关器件和直流电源的数量较少,开关频率较低等特点,并且能够降低开关上的电压应力。文献[12]介绍了一种适用于微电网系统的单相ACHB多电平逆变器,采用了直流侧电源电压不对称比为1∶2的两单元结构,能够适用于非线性负载,有比较广的适用范围。
ACHB多电平逆变器能够在输出电平数目一定时使用更少的级联单元,但由于冗余开关状态数目的减少,也对ACHB逆变器的调制策略提出了新的挑战。如果逆变器的调制策略选择不合适,ACHB逆变器的级联单元之间可能会出现电流倒灌问题,这将带来直流侧的电容电压波动,从而影响逆变器输出电压质量,同时级联单元之间也可能会出现功率分配不均衡的问题,影响逆变器效率及直流侧电源的寿命。
针对ACHB多电平逆变器出现的电流倒灌问题,文献[13-15]采用混合频率调制的方案来解决这个问题。在文献[13]中提出一种不对称比为2∶1的ACHB逆变器混合调制策略,能够保持级联单元的输出电压极性不变,然而改进的调制策略实现困难,调制信号需要在5个区间进行复杂的修改,而且开关信号需要逻辑器件进行分配。文献[14]的调制策略为全调制度下连续的脉冲宽度调制(pulse width modulation,PWM),避免了级联单元之间的电流倒灌问题,但是低压单元的开关损耗不均匀,各级联单元输出功率也无法均衡。文献[15]提出一种适用于2个单元的混合频率调制策略,能够避免级联单元间的电流倒灌问题,同时低压单元采用倍频调制提高了电压波形质量,但高压单元有部分高频开关区间,一定程度上增加了开关损耗,同时各单元输出功率没有实现均衡分配。
上述采用混合频率调制的方案能解决ACHB多电平逆变器中存在的电流倒灌问题,但都无法解决级联单元的输出功率均衡分配的问题。针对这个同样重要的问题,文献[16]中对载波进行了修改,实现了单元之间的功率均衡分配,然而该方法会产生更大的共模电压和更高的输出电压THD。文献[17]中实现了级联单元之间的均匀功率分布,然而该方案增加了器件的开关损耗,降低了逆变器的效率。文献[18]中提出一种基于单载波的PWM方案,该方案减少了载波信号的数量,并在级联单元之间保持了几乎相等的功率分布。文献[16-18]的方案解决了级联单元之间功率分配不均衡的问题,不过这些方案仅适用于直流侧电压一致的拓扑结构,进行级联单元之间的功率均衡。此外文献[19]提出一种改进的混合频率调制策略,适用于直流侧电源电压比为2∶1的ACHB逆变器,解决了单元间电流倒灌的问题,并且级联单元间保持输出功率均衡。文献[20]针对不对称比为6∶7∶8∶9的拓扑结构提出一种功率均衡方案,通过选择合适的开关模式实现级联单元之间的功率均衡分配,但是开关信号需要离线计算。文献[19-20]提出的方案仅能适用于相对应的特定拓扑,不能很好的扩展应用于其他ACHB逆变器拓扑结构,因此都具有一定的局限性。
本文首先介绍一类由单个高压单元和多个低压单元级联构成的ACHB逆变器拓扑,该拓扑具有不对称级联拓扑减少隔离电源的优势,同时还能很好的对级联单元进行扩展,其次通过对采用传统混合频率策略时逆变器级联单元的输出功率进行分析,以该类拓扑为基础提出一种通用的线性功率均衡方案,该方案的一个优点在于实现了全调制度下各级联单元输出功率按照直流侧电压比均衡分配,并且能够适用于任意级联单元数的拓扑结构,具有很好的普适性,另一个优点在于能够使低压单元的损耗保持一致,有利于解决低压单元温升不一致的问题,方便为逆变器选择合适的散热器。最后通过仿真和实验验证方案的可行性。
1 ACHB逆变器拓扑构成方案
ACHB多电平逆变器的特点在于级联单元直流侧电压有所不同,常见的一些拓扑构成方案有直流侧电源电压呈2n变化的Ⅱ型拓扑以及呈3n变化的Ⅲ型拓扑等[21-22]。Ⅱ拓扑可以通过合理的安排开关模式来达到避免电流倒灌的效果,但高压单元存在高频开关区间会提高逆变器开关损耗,同时由于各级联单元直流侧电压均不相同,难以实现各单元的输出功率均衡分配;Ⅲ型拓扑可以在保证输出电压保持连续电平阶梯时使用最少的级联单元数,但级联单元之间无法避免电流倒灌问题。
下面介绍一类新型的ACHB多电平逆变器构成方案,拓扑结构如图1所示,新型拓扑由n个单元级联而成,包含了一个高压单元和n-1个低压单元。高压单元直流侧的电源电压为mE,低压单元直流侧电源电压为E,其中需要保证m≤n-1,当配置为m=n-1时,能在相同单元数下输出最多的连续电平,因此是最推荐的级联单元电压搭配方式。
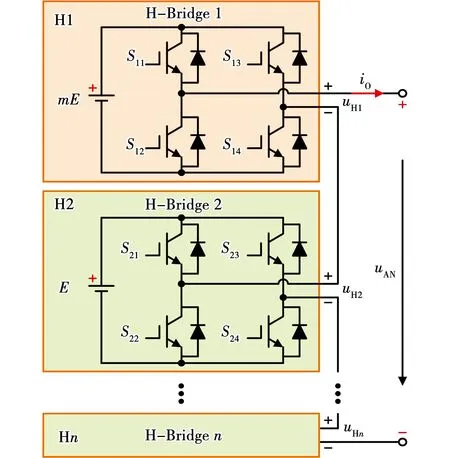
图1 逆变器拓扑结构图Fig.1 Inverter topology
在图1中H1为高压单元,H2至Hn为低压单元,逆变器输出电流为io,各单元的输出电压依次为uH1、uH2、…、uHn,逆变器的总输出电压为uAN,设i为H桥单元序号,则总输出电压为各级联单元输出电压之和为
(1)
由于每个单元均是H桥的结构,因此各单元的输出包含3种状态:正极性输出、负极性输出以及不参与输出。定义第i个单元的开关函数为Si,则Si包含3种情况,并可表示为:
(2)
结合式(1)可将逆变器输出电压表示为
(3)
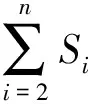
Δmax=m+n-1。
(4)
逆变器的输出电平合成方式如表1所示,由于逆变器输出负电平的方式与正电平相似,因此仅在表1中列举了输出正电平和零电平的合成方式,高压单元在电平达到m时开始工作,在m电平上下均是由低压单元之间相互配合达到输出阶梯PWM的效果,高压单元起到提供电压平台的作用。
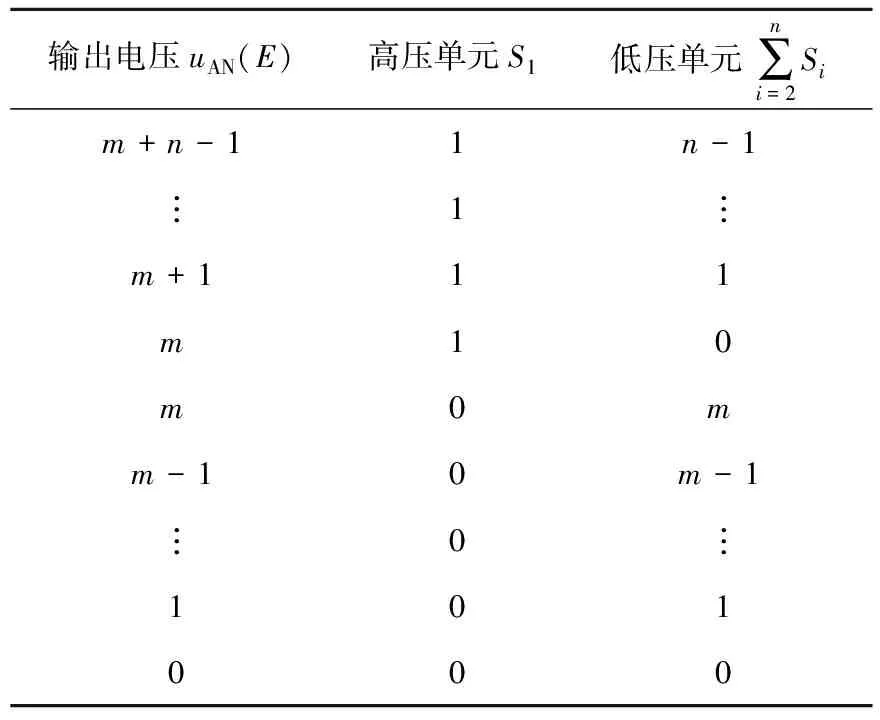
表1 逆变器输出电平合成方式Table 1 Inverter output level synthesis mode
2 不对称混合频率调制方案
2.1 传统混合频率调制策略
针对ACHB逆变器最为常见的调制方式是混合频率调制策略,其中高压单元工作在基波频率输出方波以降低开关损耗,低压单元输出高频PWM波形来保证输出电压质量。
传统混合频率调制策略原理如图2所示,其中vm是高压单元的调制波,vm与比较电平±vc1相比可以得到高压单元的开关信号,当vm>+vc1时开关函数S1=+1,高压单元输出正电平,当vm<-vc1时S1=-1,高压单元输出负电平,其他状态S1=0时高压单元输出零电平,设调制波vm的幅值为1,高压单元波形在图中可用vs表示,比较电平±vc1应按照直流侧电压比例表示为
(5)
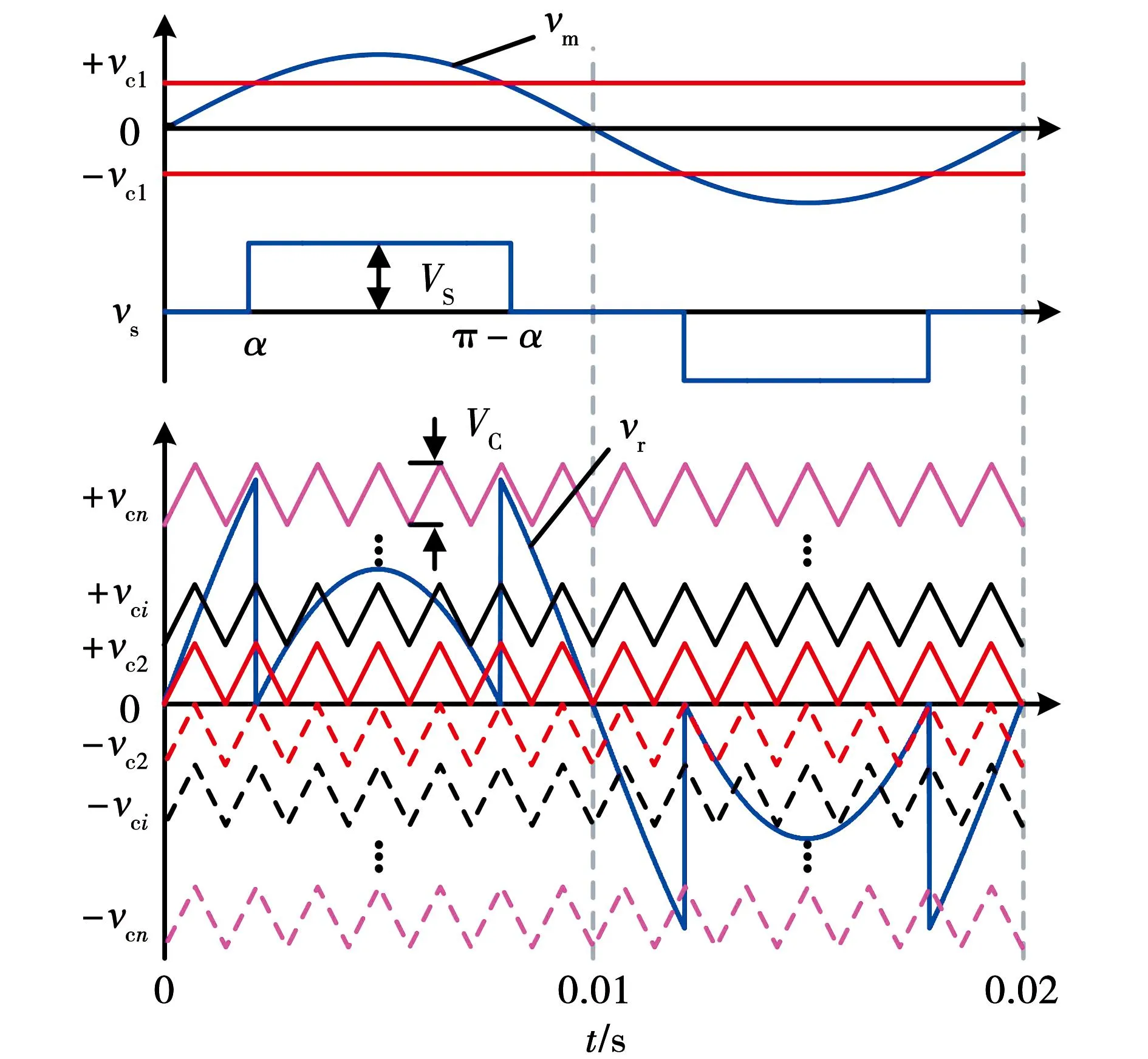
图2 传统混合频率调制Fig.2 Traditional mixed frequency modulation
高压单元的输出波形vs经过标幺化后的幅值VS也可表示为
(6)
如图2所示,vr为低压单元的调制波,vr由vm-vs得到,第i单元(i≥2)的开关信号由调制波vr与三角载波±vci比较得到,三角载波±vci的幅值VC可表示为
(7)
当vr>+vci时低压单元Hi的开关函数Si=+1,当vr<-vci时低压单元的开关函数Si=-1,其他状态保持开关函数Si=0。
2.2 单元输出功率分析
假设正弦调制波vm的角频率为ω,则vm为
vm=ΔmaxEmasin(ωt)。
(8)
式中ma(0≤ma≤1)为调制度,由图2可见,高压单元输出的波形为方波,设α为高压单元正半周期开始输出的角度,结合式(5)和式(8)可以得到α与调制度ma的关系为
(9)
高压单元输出方波的傅里叶级数展开式为
(10)
高压单元输出电压的基波电压幅值可表示为
(11)
结合式(9)和式(11)可以得到全调制度下高压单元输出电压基波幅值与调制度ma的关系为:
(12)
设第i单元的输出功率为PHi,因为各单元之间采用串联的方式,因此各单元电流的电流均为逆变器输出电流io,则各单元在周期T内输出的平均功率可表示为
(13)
式中:Io为逆变器输出电流io的幅值;φ为功率因数角。忽略逆变器输出电流波形中含有的谐波成分,io可视为基波频率的正弦波,因此各单元的输出功率可表示为基波电压电流所产生的功率。因此高压单元的输出功率可表示为:
PH1=
(14)
由式(14)可以看出,在采用传统混合频率调制略下,高压单元在调制度ma较低时输出功率为0,并且高压单元输出功率PH1与调制度ma之间是非线性关系,显然高压单元输出功率没有按照电压比均衡分配。
在采用传统混合频率调制策略时,不仅高压单元无法按照电压比分配,低压单元输出功率之间的均衡也同样存在问题。在当调制波频率远小于载波频率时,基于状态空间平均法[23]分析可知,在传统方案下低压单元的输出平均功率PHi之间非常不均衡[21]。
综上所述,在采用传统混合频率调制策略时,各单元输出功率均未按照直流侧电压比均衡分配,不利于平衡逆变器对各个级联单元的利用。
3 通用线性功率均衡方案
3.1 各单元功率均衡方法
要实现各级联单元输出功率均衡,级联单元输出功率应按照直流侧电压比例进行分配,即PH1∶PH2∶…∶PHn=m∶1∶…∶1,通过上文的分析可知,功率均衡不仅需要固定高压单元输出功率在总输出功率中的占比,而且还需要实现各低压单元之间的输出功率平均分配。
针对级联单元之间的输出功率均衡分配问题,本文在传统混合频率调制策略的基础上提出一种通用的线性功率均衡调制(linear power equalization PWM,LPE-PWM)策略,LPE-PWM策略的高压单元仍采用方波调制,不过需要对高压单元的导通角进行控制,由式(13)可知,高压单元的输出功率与高压单元输出基波电压幅值有关,输出功率占比可等效为输出电压基波幅值比,因此在功率均衡条件下高压单元输出电压基波幅值应满足:
(15)
代入式(11)可知高压单元的导通角α为
(16)
由式(16)可以看出,功率均衡时高压单元的导通角α与高压单元直流侧电压水平m以及级联单元数目n均不相关,因此本文提出的一类直流侧电压比为m∶1∶…∶1型的ACHB逆变器均可由式(16)来约束高压单元的导通角,来达到高压单元输出功率均衡的条件。
其次低压单元之间采用重构载波的思想来实现功率均衡,同时还具有相对最优的谐波特性[24]。文献[24]所介绍的半周期载波循环的方案在级联单元增多时,功率均衡所需要的时间会呈半工频周期的倍数增长,因此并不适用于级联单元较多的情况,可扩展性不够好,本文所提的LPE-PWM策略的低压单元之间采用基于载波周期的载波循环重构方法,图3为低压单元载波循环重构的方式。
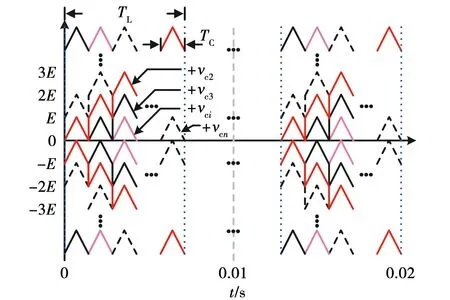
图3 载波循环重构方式Fig.3 Carrier cycle reconstruction mode
如图3所示,TC为三角载波的周期,TL为三角载波循环一个周期的时间,对于零参考线以上的载波+vci每经过一个载波周期TC便向正方向循环平移一层,因此在循环周期TL内载波+vci满足:
+vci(t+TC)=+vci(t)+E。
(17)
并且在循环周期之间满足:
+vci(t+TL)=+vci(t)。
(18)
对于零参考线以下的三角载波-vci每经过一个载波周期TC便向负方向循环平移一层,因此在循环周期TL内载波+vci满足:
-vci(t+TC)=-vci(t)-E。
(19)
同理可得三角载波-vci也满足:
-vci(t+TL)=-vci(t)。
(20)
通常载波的频率比较高,会远远大于调制波的频率,因此在载波的一个重构循环周期TL里,调制波的值可以近似等于恒值。例如,当载波频率为10 kHz,有3个低压单元级联时,选取正弦调制波斜率较大的零点到TL时刻进行计算,此时第一个和最后一个三角载波对应的正弦调制波采样值之间仅相差0.06左右。在实际应用中,三角载波频率往往还会在10 kHz以上,因此在分析时调制波的值在重构循环周期内可以近似等于恒值。
图4为在一个循环周期内各低压单元的正半周期输出电压方式,以电压区间[0,E]为例对输出电压进行分析,由于载波周期TC内调制波vr近似为恒值,则各单元占空比均相等,并定义为d,则可以得到位于第一层载波内各个低压单元在循环周期里的输出平均电压为
(21)

图4 循环周期内各低压单元输出方式Fig.4 Output mode of each low voltage unit in the cycle
由图3的载波循环规律可知,1个循环周期内各载波±vci在每一层均只占有一个三角载波,则只有1个相交的载波会输出占空比d的波形,上方载波输出占空比为0,下方载波输出占空比为1,则当调制波vr位于第j层时,则可以等效得到各单元输出平均电压为
(22)
由式(22)可知,无论调制波vr在任何一层,即任何一个电压区间,各低压单元的输出平均电压均相等[20],因此各低压单元输出电压的基波可表示为
(23)
结合式(13)、式(15)和式(23)可知,各级联单元的输出功率可表示为:
(24)
因此本文所提的LPE-PWM策略能够使得输出功率在各级联单元之间均衡分配,达到功率均衡的目的,各单元输出功率之间关系为
PH1∶PH2∶… ∶PHn=m∶1∶… ∶1。
(25)
3.2 低压单元开关损耗分析
低压单元开关管的损耗可以分为导通损耗和开关损耗,由图4的分析可知,在LPE-PWM策略下每个低压单元开关管的开关次数以及占空比均保持一致,假设开关管的等效开关频率为fSW,每个单元均含有4个开关管,因此每个低压单元的开关损耗均可表示为
(26)
其中ESW(on)、ESW(off)分别是开关管开通和关断时的能量损失。
根据文献[25]中损耗计算方式,由于每个开关管在一个周期内只有一半时间有电流流过,一个低压单元含有4个开关管,因此低压单元的通态损耗可以表示为
(27)
结合文献[25]中的等效模型,由图4分析可知,在LPE-PWM策略下低压单元的占空比可表示为
τHi(t)=Δmaxmasin(ωt+φ)。
(28)
流过开关管的电流iC等于逆变器输出电流io,结合式(27)与式(28)可得低压单元的通态损耗为
(29)
式中:VCE0为开关管门槛电压;rCE为开关管通态电阻,均可从开关管的使用手册中获得。
各低压单元的通态损耗PSS(Hi)可由式(29)计算,由于流过各低压单元的电流均为逆变器输出电流io,在低压单元选择相同IGBT的情况下,各低压单元的通态损耗保持一致,又因为通过上节的分析可知每个低压单元的开关频率fSW基本保持一致,因此各低压单元的损耗PLS(Hi)均相等,并可表示为
PLS(H2)=PLS(H3)=…=PLS(Hi)=PSW(Hi)+PSS(Hi)。
(30)
3.3 应用案例
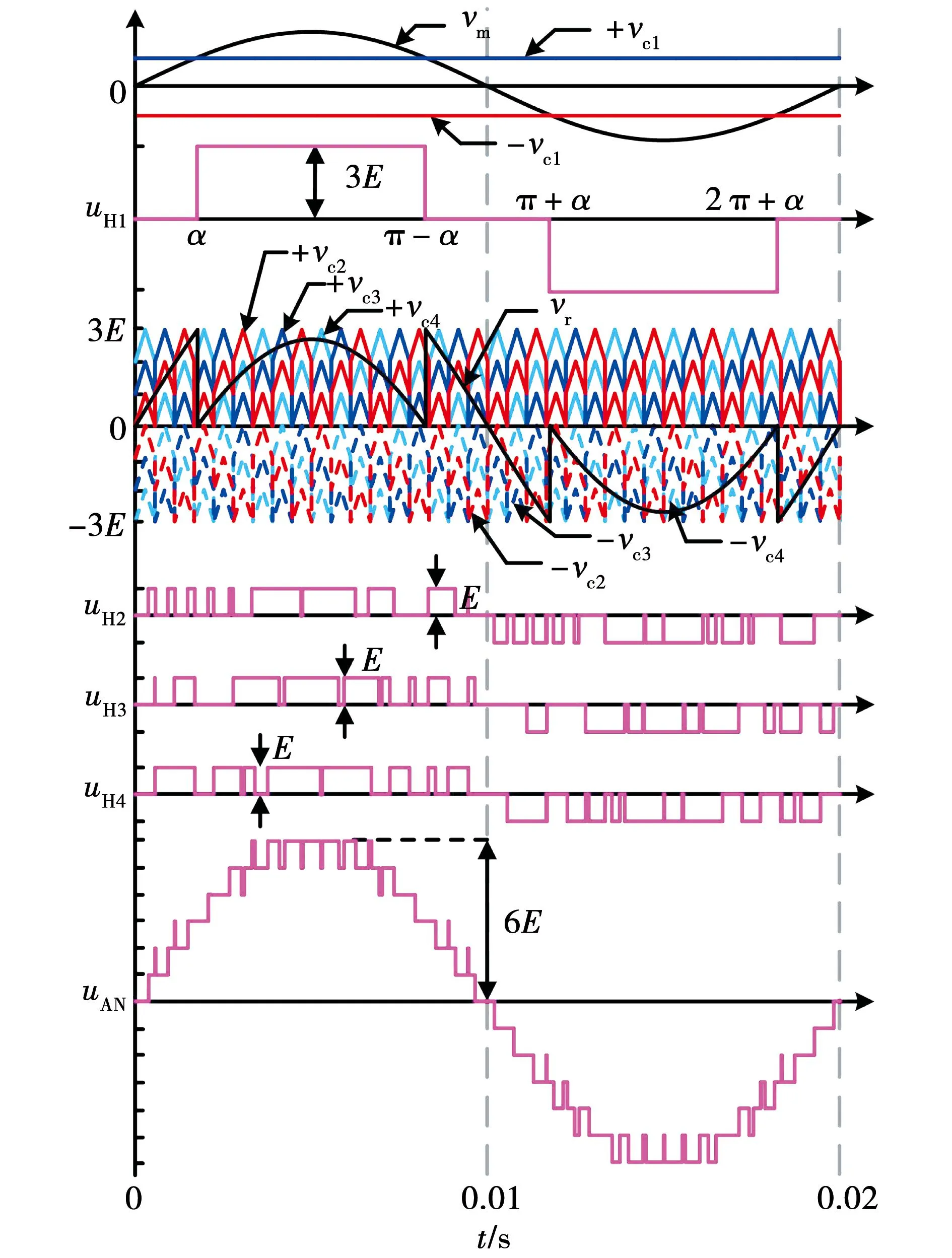
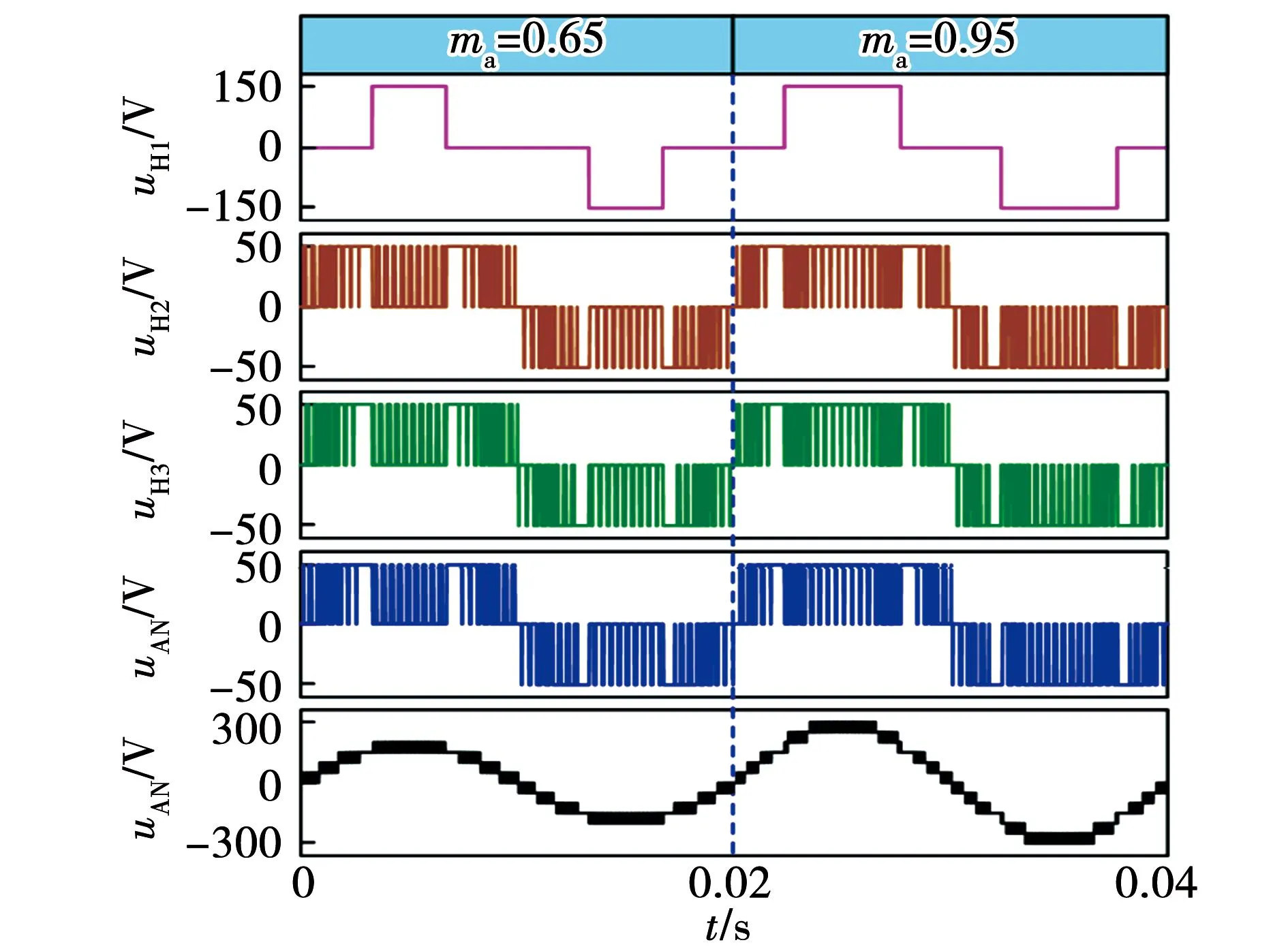
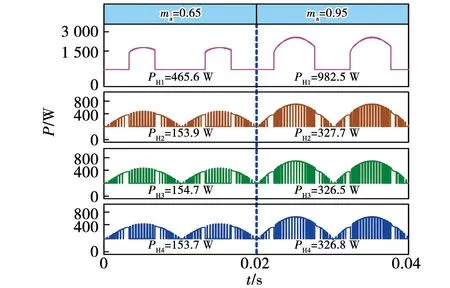
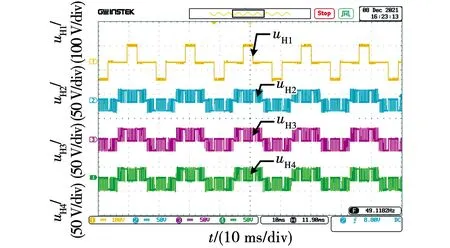
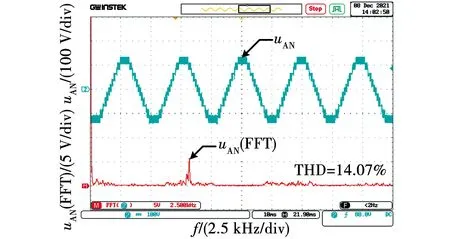
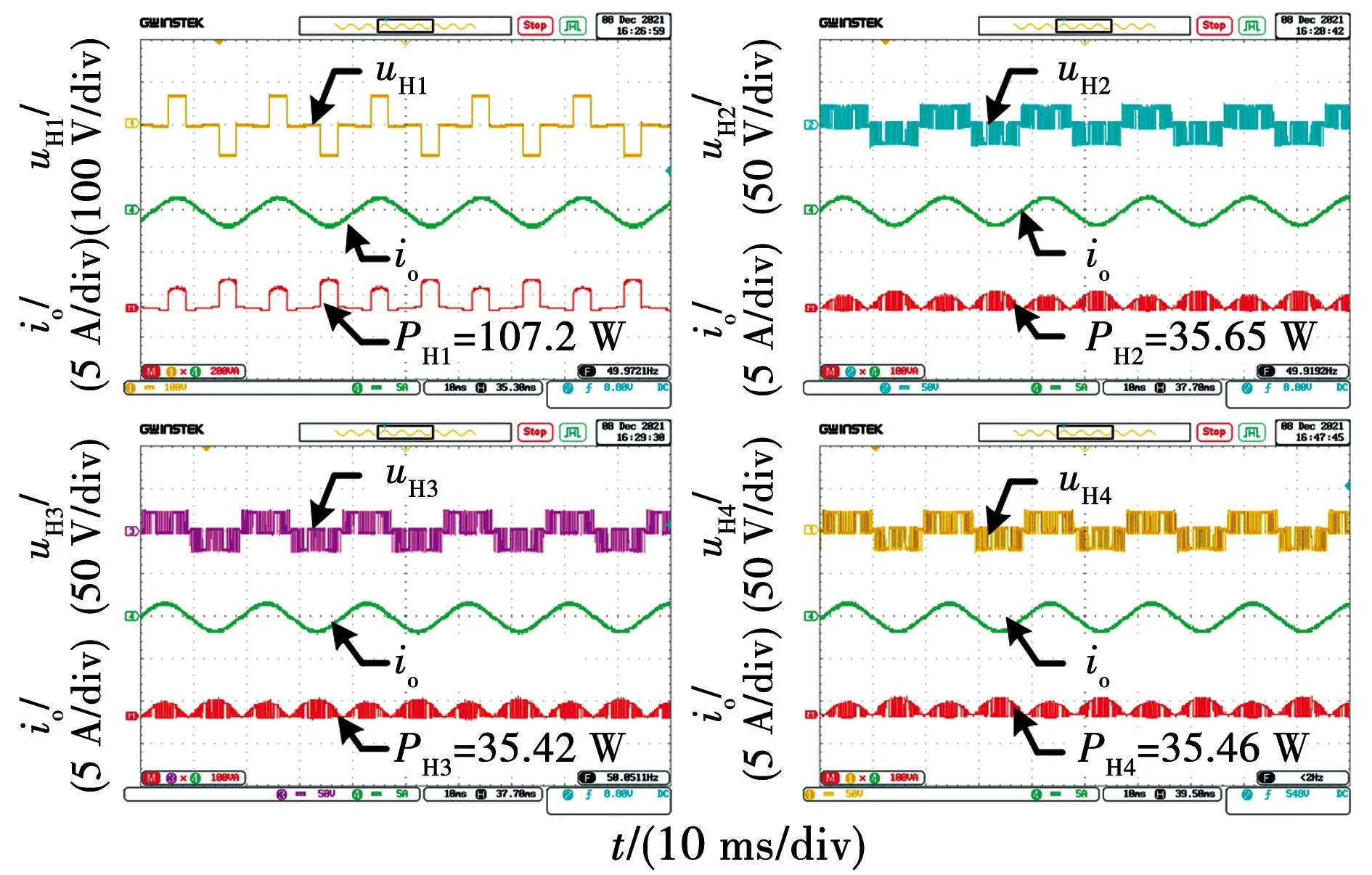
为了更为清晰的表示LPE-PWM策略应用时的工作原理,下面针对m 图5为2∶1∶1∶1型结构的调制原理图,调制波vm的峰值为直流侧电压之和5E,比较电平±vc1的绝对值由开关角α决定,结合式(8)和式(16)可知 (31) 图5 逆变器调制原理(2∶1∶1∶1)Fig.5 Modulation principle of inverter(2∶1∶1∶1) 高压单元输出电压幅值为2E,低压单元的调制波信号vr为vm减去高压单元输出信号,调制波正半周期由+vc2、+vc3和+vc4进行调制,负半周期由-vc2、-vc3和-vc4进行调制。由图5中可以看出,正半周期的载波均为从原点向纵轴正方向依次上升循环的三角载波构成,以载波+vc2为例,没过一个周期载波便向上平移一个电压区间,在达到最高层电压区间后再循环回第一层,这种循环方式使得每个载波占据3个正电平区间的次数是基本相同的,负半周期的载波循环方式与正半周期类似,不过载波是向纵轴负方向依次循环。 以低压单元H2为例来说,当vm>+vc2时,开关S21的信号为高电平,处于导通状态,开关S22与之互补为关断状态,此时低压单元H2输出正向+E电压,当vm<-vc2时,开关S23的信号为高电平,处于导通状态,开关S24与之互补为关断状态,此时单元H2输出反向-E电压。由单元H2的输出电压波形可以看出,H2单元在整个周期内均断断续续有电压输出,体现了载波循环重构的效果。单元H3和单元H4的调制原理与H2类似,分别由载波±vc3和±vc4分别进行调制。总体来看3个低压单元的输出波形保持比较均匀的分布,各个低压单元工作的时间基本平均,大致可以看出各个低压单元的输出相对均衡。 此外如图5所示,级联的高压单元输出开关角度可控的基频方波,各低压单元输出分布均衡的PWM波形,以此来达到各单元输出功率均衡的目的,同时所有级联单元的输出极性保持一致,逆变器最高输出电平为5E,由高压单元和3个低压单元叠加得到,输出电压最高可达十一电平。 图6为3∶1∶1∶1型拓扑结构的调制原理图,调制波vm的峰值为直流侧电压之和6E,与2∶1∶1∶1型类似导通角α由式(16)约束,可知 (32) 图6 逆变器调制原理(3∶1∶1∶1)Fig.6 Modulation principle of inverter(3∶1∶1∶1) 3∶1∶1∶1型拓扑的低压单元调制与2∶1∶1∶1型类似,不同之处在于高压单元输出电压幅值为3E,因此低压单元的调制波vr需要减去幅值为3E的方波,即减去高压单元的输出波形。低压单元的载波同样是采用纵向循环的方式,保持各单元的载波在每个电压区间均衡分配,达到均衡低压单元输出的目的。由于高压单元输出电压幅值为3E,逆变器输出总电压的最高电平数可达十三电平。 为验证所提LPE-PWM策略的正确性,使用Simulink搭建仿真模型,仿真模型参数设置如下,级联单元直流侧的单位电压E=50 V,负载电阻值为20 Ω,滤波电感为4 mH,调制波频率为50 Hz,三角载波频率设置为8 kHz。通过分析LPE-PWM策略的工作原理可知,LPE-PWM策略应用在结构Ⅰ型和结构Ⅱ型上具有相同的功率均衡效果,因此在理论验证上区别并不大,并且Ⅱ型拓扑相对可以输出更多的电平数目,因此仿真仅以3∶1∶1∶1型拓扑结构作为对象进行验证。 图7为逆变器的输出电压波形,3∶1∶1∶1型逆变器的高压单元直流侧电压为150 V,高压单元输出方波,在调制度ma从0.65变为0.95时,高压单元的导通角随之变化,符合式(16)的规律,低压单元输出PWM波,从图中可以看出,各低压单元的输出电压波形基本保持一致,有着相同的开关频率,在高调制度ma=0.95时,逆变器能够输出十三电平,达到最大输出电平数。 图7 逆变器输出电压波形Fig.7 Output voltage waveform of inverter 图8为逆变器的输出功率波形图,由图中可以看出,在不同的调制度下各单元的输出功率均能保持均衡,在调制度ma=0.65时,高压单元H1输出功率为465.6 W,低压单元H2、H3和H4的输出功率分别为153.9、154.7和153.7 W,在调制度ma=0.95时,高压单元H1输出功率为982.5 W,低压单元H2、H3和H4的输出功率分别为327.7、326.5和326.8 W,可见在不同调制度下,各单元输出功率基本保持均衡,按照3∶1∶1∶1进行分配。 图8 逆变器输出功率波形Fig.8 Output power waveform of inverter 图9为逆变器输出功率与调制度的关系图,如图所示,各单元的输出功率在全调制度下均与调制度之间保持线性关系,并且各单元输出功率之间按照3∶1∶1∶1均衡分配,达到了LPE-PWM策略线性功率均衡的效果。 图9 逆变器输出功率与调制度的关系Fig.9 Relationship between output power and modulation of inverter 图10为逆变器的输出电压频谱图,从图中可以看出,逆变器输出电压的谐波主要分布在载波比160次的整数倍及附近,在ma=0.65时,输出电压波形的THD为17.22%,基波分量的幅值为193.5 V,在ma=0.95时,输出电压波形的THD为12.49%,基波分量的幅值为283.1 V。 图10 逆变器输出电压频谱Fig.10 Output voltage spectrum of inverter 为进一步的验证LPE-PWM策略的可行性,搭建一台试验样机进行实验验证,样机是直流侧电压比为3∶1∶1∶1的Ⅱ型拓扑结构,高压单元直流侧电源电压为72 V,低压单元均为24 V,负载电阻为50 Ω,滤波电感为4 mH,调制波频率为50 Hz,三角载波频率设置为8 kHz,试验样机采用FPGA作为控制器。 图11为采用LPE-PWM策略下各单元输出电压波形,其中调制度为ma=0.65。从图中可以看出高压单元输出电压波形为方波,低压单元的输出电压波形均为PWM波,波形比较相似,并且在一个周期内的开关次数也基本一致。 图11 各单元输出波形(ma=0.65)Fig.11 Output waveform of each unit (ma=0.65) 图12为调制度ma=0.65时逆变器的输出电压波形及频谱,从图中可见,逆变器总输出为九电平阶梯PWM波形,输出电压中的谐波主要集中在载波比160次的整数倍及附近,输出电压THD=14.07%。 图12 逆变器输出波形(ma=0.65)Fig.12 Inverter output waveform(ma=0.65) 图13为在调制度ma=0.95下逆变器各单元输出电压波形。可以看出高压单元输出电压波形仍为方波,由于高压单元输出功率与导通角有关系,所以高调制度的方波更宽,低压单元输出为PWM波。 图13 各单元输出波形(ma=0.95)Fig.13 Output waveform of each unit(ma=0.95) 图14为调制度ma=0.95时逆变器的输出电压波形及频谱,由图可见,逆变器总输出为十三电平阶梯PWM波形,输出电压THD=14.07%。 图14 逆变器输出波形(ma=0.95)Fig.14 Inverter output waveform (ma=0.95) 图15和图16分别为调制度ma=0.65和调制度ma=0.95下各单元的输出功率波形,经测量在图15中各单元的输出功率分别为107.2、35.65、35.42和35.46 W。同样经测量在图16中各单元输出功率分别为227.6、75.23、75.29和75.51 W,可见在不同调制度下,LPE-PWM策略均能使各单元输出功率保持均衡分配。 图15 输出功率波形(ma=0.65)Fig.15 Output power waveform (ma=0.65) 图16 输出功率波形(ma=0.95)Fig.16 Output power waveform (ma=0.95) 图17为不同调制度下低压单元开关管的温度图,从左至右分别为低压单元H2、H3和H4的开关管温度。实验条件为在室温10 ℃稳定工作10 min,在调制度ma=0.65下,低压单元H2、H3和H4开关管温度分别为26.3、26.7和26.4 ℃。在调制度ma=0.95下,低压单元H2、H3和H4开关管温度分别为30.8、31.2和31.0 ℃。可见在不同调制度下,各单元开关管的温升基本一致,说明各低压单元的开关管损耗也基本保持一致。 图17 开关管温度图Fig.17 Switch temperature diagram 本文分析了传统混合频率调制策略直接应用在ACHB多电平逆变器上的局限性,以级联各单元之间的输出功率均衡分配为目标,提出一种通用的线性功率均衡调制策略,能够有效平衡各级联单元的输出功率。通过理论分析以及仿真实验表明: 1)本文所提出的LPE-PWM策略应用在一类m∶1∶…∶1型的不对称拓扑上时,能够保持各级联单元输出功率按照直流侧电压比均衡分配,并且在扩展低压单元时仍能保持功率均衡的效果。 2)LPE-PWM策略能够在全调制度下保持各级联单元输出功率均衡,高压单元从0线性增加到0.5mamEIocosφ,低压单元从0线性增加到0.5maEIocosφ。 4)在采用LPE-PWM策略后,各低压单元开关管的损耗能够基本保持一致,保证开关管具有相同的温升,有利于逆变器散热器的设计。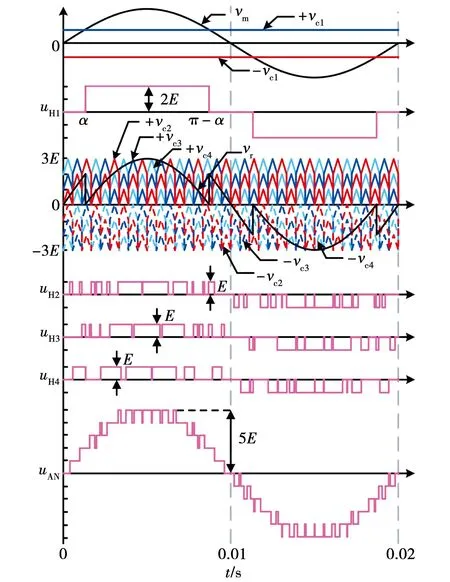
4 仿真分析


5 实验验证




6 结 论