模块化定子混合励磁同步电机磁网络建模与分析

吴胜男, 庞先文, 佟文明, 王玉坤

(沈阳工业大学 国家稀土永磁电机工程技术研究中心, 辽宁 沈阳 110870)

0 引 言

与传统的电励磁同步电机及永磁同步电机相比,混合励磁电机避免了大量的励磁损耗导致电机效率低下以及永磁体退磁的问题[1]。由于其具有永磁发电机无刷、可靠以及调压方便的优点[2],所以被广泛应用于电动混合动力汽车驱动以及风力发电等领域[3]。

对混合励磁电机进行静态特性计算与电磁性能预测有很多种方法,包括解析法[4-7]、等效磁网络法[8-12]、有限元法等。解析法具有计算速度快、精度高、对计算机设备性能要求低等特点,但解析法在计算时过于简化模型,如假设了定子铁心和转子背轭磁导无穷大而导致计算无法考虑铁心材料非线性变化带来的影响,计算并不准确[13]。

等效磁网络法采用磁路和电路类比的方法,在计算时首先考虑了电机的几何形状,同时考虑了电机漏磁、磁饱和、电枢反应和转子旋转等因素,其计算结果相对比较准确,计算过程得益于MATLAB程序的广泛应用,可以在较短的计算时间内完成相对精确的磁场计算,适用于电机初始磁场计算和优化设计[14]。

如今,磁网络已经被广泛用于各类电机的电磁特性分析,如开关磁阻电机[15]、永磁无刷电机[16]、内置式永磁电机等[17-18]。文献[19]将一台轴向磁通电机径向分层,将电机简化为多个直线电机进行建模分析;文献[20]对一台混合励磁三维轴向磁通电机建立了三维磁网络模型,该模型综合考虑了磁通边缘效应、斜槽、静态和动态偏心、槽漏磁以及多类型激励等多方面因素。文献[21]磁网络模型引入考虑磁动势和反作用磁通量的分支磁路,进而引入了涡流效应。文献[22]提出了模块化等效磁网络建模思路和具有通用性的气隙等效磁网络模型,在气隙模型中引入了一种耦合的可变磁导单元,该单元捕获轴向和周向气隙磁通密度。借助于耦合可变磁导元件,通过气隙和转子的时变连接来考虑瞬态磁场。

目前对于混合励磁电机的性能分析多以有限元方法为主,本文旨在提供一种高效准确的分析方法并避免有限元耗时长的弊端。以一台电动汽车用新型模块化定子交替极转子结构的新型混合励磁同步电机为研究对象,提出一种三维磁网络解析模型,模型中考虑电机的定子齿顶饱和、槽漏磁、端部漏磁、电枢反应、转子转动等因素。同时利用该模型计算分析新型混合励磁同步电机的气隙磁密、磁链、反电动势与电磁转矩等特性,利用有限元结果验证准确性,并计算分析新型混合励磁同步电机的调磁性能。

1 混合励磁同步电机结构与工作原理

1.1 新型混合励磁同步电机结构

新型模块化定子混合励磁同步电机的基本拓扑结构如图1所示。定子部分采用模块化结构,定子齿与定子轭分别加工后通过燕尾槽连接,电枢绕组与励磁绕组均缠绕在定子齿上,电励磁绕组沿轴向分为两段且电流方向相反,省去了电刷与滑环结构,提高了电机的可靠性,同时电机定子侧采用非晶合金材料代替了常用的硅钢片结构,减小了电机的铁耗,提升了电机的效率。转子侧采用实心交替极结构,沿轴向分为两段,依次放置永磁体磁极与铁磁极,周向方向上永磁体磁极与铁磁极交错排列,铁磁极为电励磁提供通路,电机基本参数如表1所示。

表1 新型混合励磁同步电机基本参数

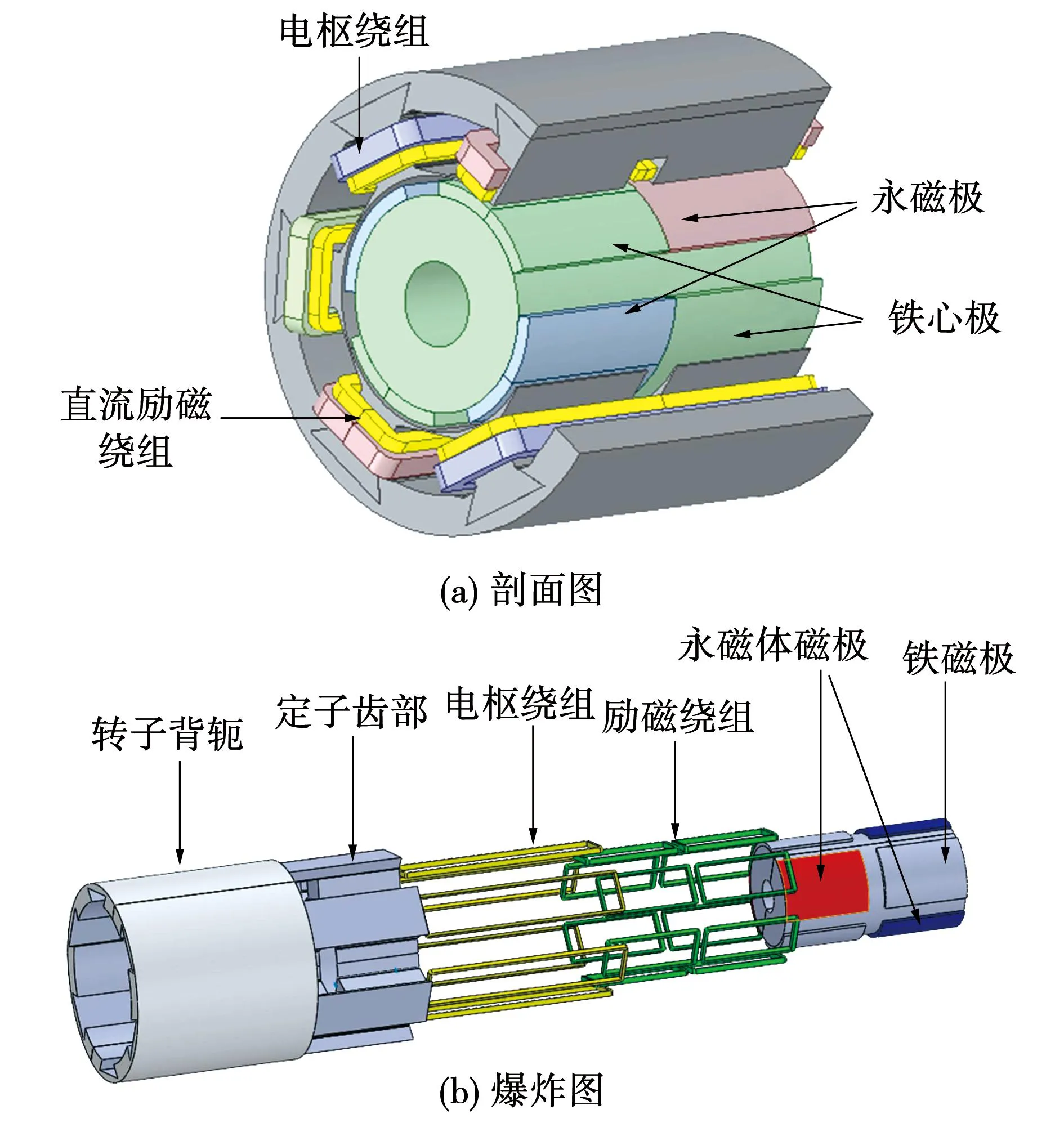
图1 混合励磁同步电机基本拓扑结构Fig.1 Basic topology of a hybrid excitation synchronous motor

1.2 新型混合励磁同步电机工作原理

新型混合励磁同步电机存在3种工作状态,即永磁体单独励磁状态、直流励磁增磁状态与直流励磁去磁状态。当电机工作在永磁体单独励磁状态时,直流励磁电流为0,其磁通由永磁体N极出发经过气隙、定子齿、定子周向轭部、定子轴向轭部回到永磁体S极,此时铁磁极不作为磁通路径;当工作在增磁状态时,周向方向上临近N极的铁磁极经磁化显“S”,临近S极的铁磁极经磁化显“N”,磁通沿周向由N极到S极,这种情况下,电机每极下磁通增强;当工作在去磁状态时,周向方向上临近N极的铁磁极经磁化显“N”,临近S极的铁磁极经磁化显“S”,磁通沿轴向由N极到S极,这种情况下,电机每极下磁通减弱,如图2所示。

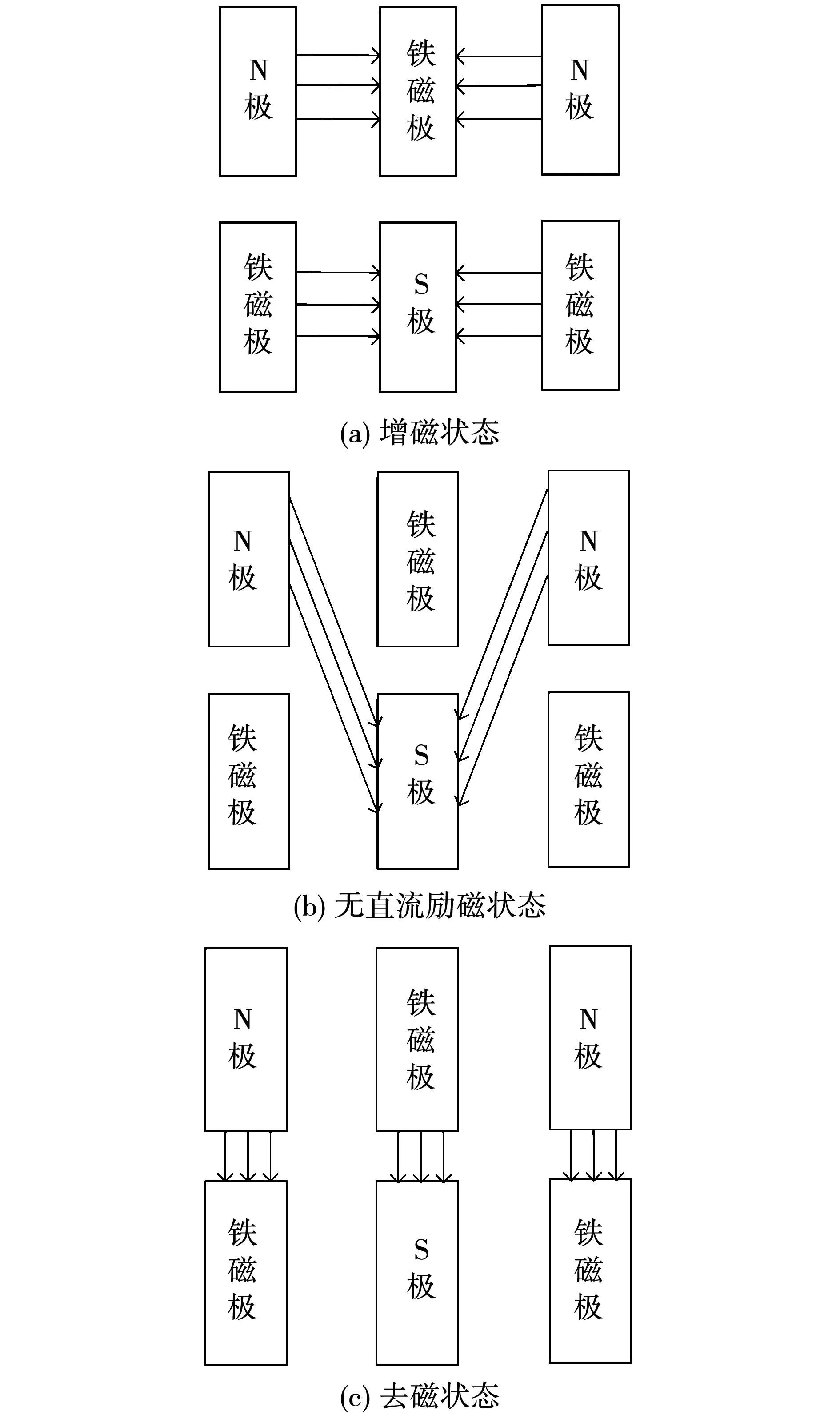
图2 电机工作原理示意图Fig.2 Schematic diagram of working principle of the motor

2 混合励磁同步电机三维磁网络建模

2.1 模块化定子齿磁网络建模

新型混合励磁电机定子侧简化磁网络模型如图3所示,其中:Gsy为定子周向轭部磁导;Gst为定子齿根磁导。

图3 定子简化磁网络模型Fig.3 Simplified stator magnetic network model

图4 定子齿部磁导分割Fig.4 Stator tooth permeability division

2.2 定转子相对位置

当电机中磁场尚未达到饱和时,气隙处的空气磁导率远远小于铁心的磁导率,因此气隙磁阻远大于铁心磁阻,气隙等效磁导对于磁网络计算的精确性有很大影响,又因为等效磁路法计算的是某一瞬态时刻电机的参数,而电机的转子在不停地转动,气隙与定转子之间的相对位置也在不停地变化,以永磁N极与A相绕组正对位置为起始位置,模块化定子混合励磁电机采用集中绕组,起始位置即永磁极正对A相定子齿位置,此时A相磁链为最大值,同时以A相定子齿为参考点,转子从初始位置开始转动,直到铁心极转到A相绕组正对位置,此时磁链达到最小值,这时通过计算可以得到半个电周期的磁链与反电势波形,根据磁链对称性即可得到完整的磁链反电势波形。为了考虑这种定转子之间相对的位置变化,同时由于本文将定子齿尖分割为22个磁导,按照转子的转动规律,将半个电周期内的转子同样划分为22个区域,分别为θ0～θ22,在每个区域内,转子磁极与气隙、定子的连接情况都不同,电机定转子相对位置划分如图5所示。

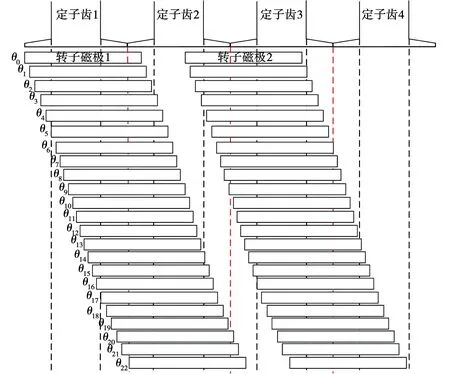
图5 定转子相对位置Fig.5 Relative position of stator and rotor

同时,根据定转子之间相对位置不同,气隙磁通路径也有所不同,经过分析,可以得到如图6所示的几种典型磁通管,计算公式为:

(1)

图6 气隙磁通管Fig.6 Air gap flux tube

(2)

式中:GA与GB分别为A类与B类磁通管;μ0空气磁导率;l为电机定子齿周向长度;g为气隙长度。

2.3 定子槽漏磁

漏磁也是影响磁网络建模准确性的一个关键因素,电机定子槽内存在磁力线只与绕组匝链而不经过气隙,因此电机槽内存在漏磁路径,如图7所示,根据磁通路径将其分割为矩形与两个梯形结构,磁导计算公式为

(3)

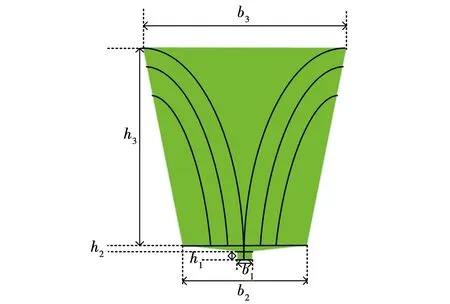
图7 定子槽漏磁示意图Fig.7 Schematic diagram of stator slot leakage reactance

其中Gsδ为槽内漏磁导。

2.4 磁极端部漏磁与极间漏磁

新型混合励磁同步电机存在磁极间端部漏磁与磁极极间漏磁,如图8所示为电机在增磁状态时磁极的端部漏磁与极间漏磁示意图,为方便求解,对漏磁路径进行了分割处理,端部漏磁可以分解为一个矩形与两个半圆磁通管,极间漏磁可以分解为一个矩形和两个1/4圆磁通管,其计算公式为:

(4)

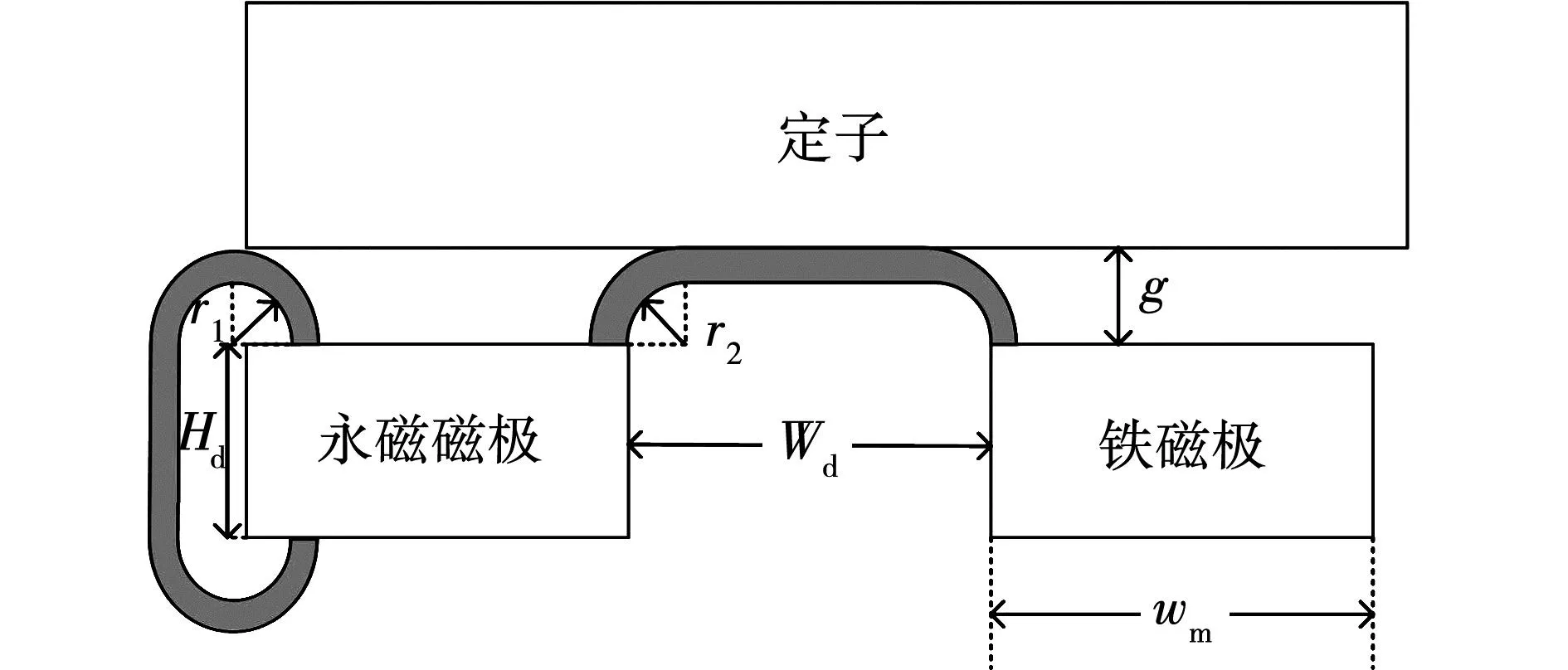
图8 电机转子磁极漏磁Fig.8 Rotor magnetic pole leakage of the motor

(5)

(6)

式中:Gc-l为增磁状态下周向磁极极间漏磁导;Ga-l为去磁状态下轴向磁极极间漏磁导;Gend为磁极端部漏磁导;lm为磁极轴向长度;wm为磁极宽度;Wd为周向磁极间距离;Wd-axial为轴向磁极间距离;Hd为磁极磁化方向长度。r1与r2分别为端部漏磁与极间漏磁分割后圆形磁通管的半径。

2.5 新型混合励磁同步电机三维磁网络模型

假设定子与气隙磁网络模型的连接在瞬态计算时是固定不变的,转子与气隙磁网络的相对连接位置通过关联矩阵与转子区域划分进行考虑,如图9所示为搭建好的新型混合励磁电机一对极下的转子处在θ4位置时的单元电机三维磁网络模型。该模型结合了前面描述的定转子、气隙及漏磁模型,其中:FAC为电机电枢磁动势;FDC为电机直流励磁磁动势;FPM为永磁体等效磁动势;Gst为定子齿根磁导;Gtt为定子齿尖磁导;Gsy为定子周向轭部磁导;Ga-sy为定子轴向轭部磁导;Gsδ为定子槽漏磁导;Gg为气隙磁导,包括A类磁通管与B类磁通管;GPM为永磁体磁极等效磁导;Giron为铁磁极等效磁导;Gr为转子磁导;Ga-l为电机轴向磁极极间漏磁导;Gc-l为电机周向磁极极间漏磁导;Gend为磁极端部漏磁导。

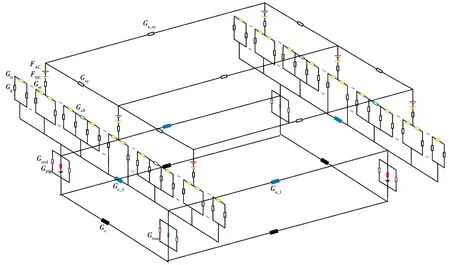
图9 新型混合励磁电机三维磁网络模型Fig.9 Three-dimensional magnetic network model of novel hybrid excitation motor

2.6 非线性迭代及磁网络求解

在对磁网络模型求解时,可以利用其与电路的相似性,采用节点电压法进行求解,得到节点电压方程矩阵:

AGATFn=AΦ;

(7)

(8)

(9)

其中:A为关联矩阵;G为各支路磁导矩阵;G(i,j)为节点i与节点j之间的磁导;Fn为各支路磁动势矩阵;Φ为各支路磁通矩阵。

由于新型混合励磁电机定子采用非晶合金材料,而铁磁材料受到非线性B-H特性曲线的影响,磁导率将发生变化,因此要对铁磁材料的磁导率进行迭代求解,其步骤如下:

1)设置迭代终止误差ε0,假设各磁导初始磁导率μ(0),根据前文磁势矩阵计算各磁导的磁密为

(10)

2)通过新计算得到的磁密Bi(k),通过B-H曲线得到磁导率μ(k),利用插值公式加快迭代,即

μ(k+1)=μ(k-1)0.95μ(k)0.05。

(11)

3)计算两个迭代前后磁导率误差εend,当εend<ε0时,跳出循环并结束,当εend>ε0时,返回第2)步继续迭代计算。

3 有限元分析及验证

3.1 气隙磁密

由于电机除周向磁路外还存在轴向磁路,通过有限元法得到电机处在无直流励磁状态、电流为2 A的增磁励磁状态与电流为-2 A的去磁励磁状态下的三维气隙磁密如图10所示。

图10 电机三维气隙磁密Fig.10 3-D air gap flux density of motor

为验证三维磁网络模型的准确性,如图11为采用所搭建的磁网络模型计算电机处在θ4位置时三种状态下轴向平均半径分别为+35 mm与-35 mm处的气隙磁通密度结果并与有限元对比。

图11 气隙磁密对比图Fig.11 Air gap magnetic density comparison diagram

结果表明,有限元法与等效磁网络法得到的气隙磁密基本吻合,并且在通以2 A与-2 A励磁电流时对永磁磁极的气隙磁密有所影响,增磁状态下永磁磁极磁密有所增加,去磁状态下永磁磁极磁密有所降低。

3.2 磁链与反电势

磁链与反电势可以通过下式计算:

ψ=N·B·S;

(12)

(13)

其中:N为线圈匝数;B与S分别为定子齿的磁通密度与线圈横截面积。图12为有限元与磁网络解析计算的磁链比较结果,图13为有限元与磁网络解析计算的反电动势对比结果,可以看出磁网络计算结果与有限元方法分析结果较为接近,验证了三维磁网络模型的正确性。

图12 磁链对比图Fig.12 Flux linkage comparison diagram

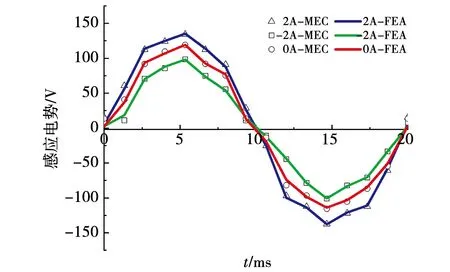
图13 反电势对比图Fig.13 Induced voltage comparison diagram

4 混合励磁同步电机性能分析

4.1 调磁能力分析

新型混合励磁同步电机调节磁场的本质是通过电励磁绕组产生的磁通量来改变气隙合成磁通。

新型混合励磁同步电机在转子转动时,会产生两种磁链,分别为永磁体产生的永磁磁链与励磁电流产生的电励磁磁链,当两种磁链方向相同时,对电机起增磁作用,方向相反时,起去磁作用。对电机施以不同的电励磁电流就可以起到调节磁场的作用,分别通入±4 A、0 A与±2 A的励磁电流,采用磁网络与有限元两种方法计算对比空载A相磁链的变化如图14所示,对电机的调磁能力分析如图15所示。

图14 不同励磁电流下空载磁链波形对比图Fig.14 Different excitation currents no-loaded flux linkage comparison diagram

图15 调磁能力分析Fig.15 Magnetometric capability analysis

通过对A相磁链的变化分析可知:

1)电枢绕组磁链随励磁电流变化明显,电机具有良好的调磁能力;

2)在通以2 A与4 A励磁电流时,相磁链相较于无励磁时分别增加了22.68%与45.36%,而在通以-2 A与-4 A励磁电流时,相磁链分别降低了13.45%与24.9%,因此电机的增磁能力要优于弱磁能力,即电机在低速状态时提升转矩能力更佳;

3)磁链随励磁电流的变化非线性。这是由于随着励磁电流增大,铁磁材料趋于饱和,磁阻逐渐增大,降低了调磁效率。

4.2 转矩分析

计算得到电机的三相磁链后,通过Clark与Park变换得到电机dq轴磁链如下:

(14)

(15)

其中δ为d轴与A相轴线间的夹角。

同样,d轴与q轴电流也可以通过坐标变换得到,即

(16)

电机电磁转矩可以通过下式计算得到:

(17)

图16为电机电枢绕组电流幅值为2A,电流角为0°时,磁网络解析计算与有限元结果的电磁转矩对比图,可以看出,采用磁网络解析计算得到的结果要略小于有限元分析的结果,为了进一步分析造成这种现象的原因,对电机在不同电流角下的平均转矩进行计算与仿真,其结果曲线如图17所示。

图16 电磁转矩对比图Fig.16 Electromagnetic torque comparison diagram

图17 不同电流角下平均转矩对比图Fig.17 Comparison chart of average torque at different current angles

由图17可以看出,电机的平均转矩大小与电流角有关,同时,采用磁网络与有限元法计算转矩结果的差异也会随着电流角而变化,这是由于在不同的电流角度下,电机存在不同的磁饱和区域,这些过饱和区域影响了磁网络计算的准确度,但是由此造成的差异并不大,这也验证了磁网络模型的准确性。

永磁同步电机采用变频调速方式调速时,当电机转速低于额定转速,其输出转矩保持恒定,此时的输出功率较小。而模块化定子混合励磁同步电机可以通过低速时电励磁增磁解决这一问题,采用id=0控制时混合励磁电机的电磁转矩为

(18)

其中:Te为电磁转矩;p为永磁体极对数;ψm为永磁体磁链;Msf为d轴绕组与电励磁绕组之间的互感;if为电励磁电流;iq为q轴电枢电流,采用磁网络与有限元的方法分别计算了在不同励磁电流下电机平均转矩的变化,如图18所示。

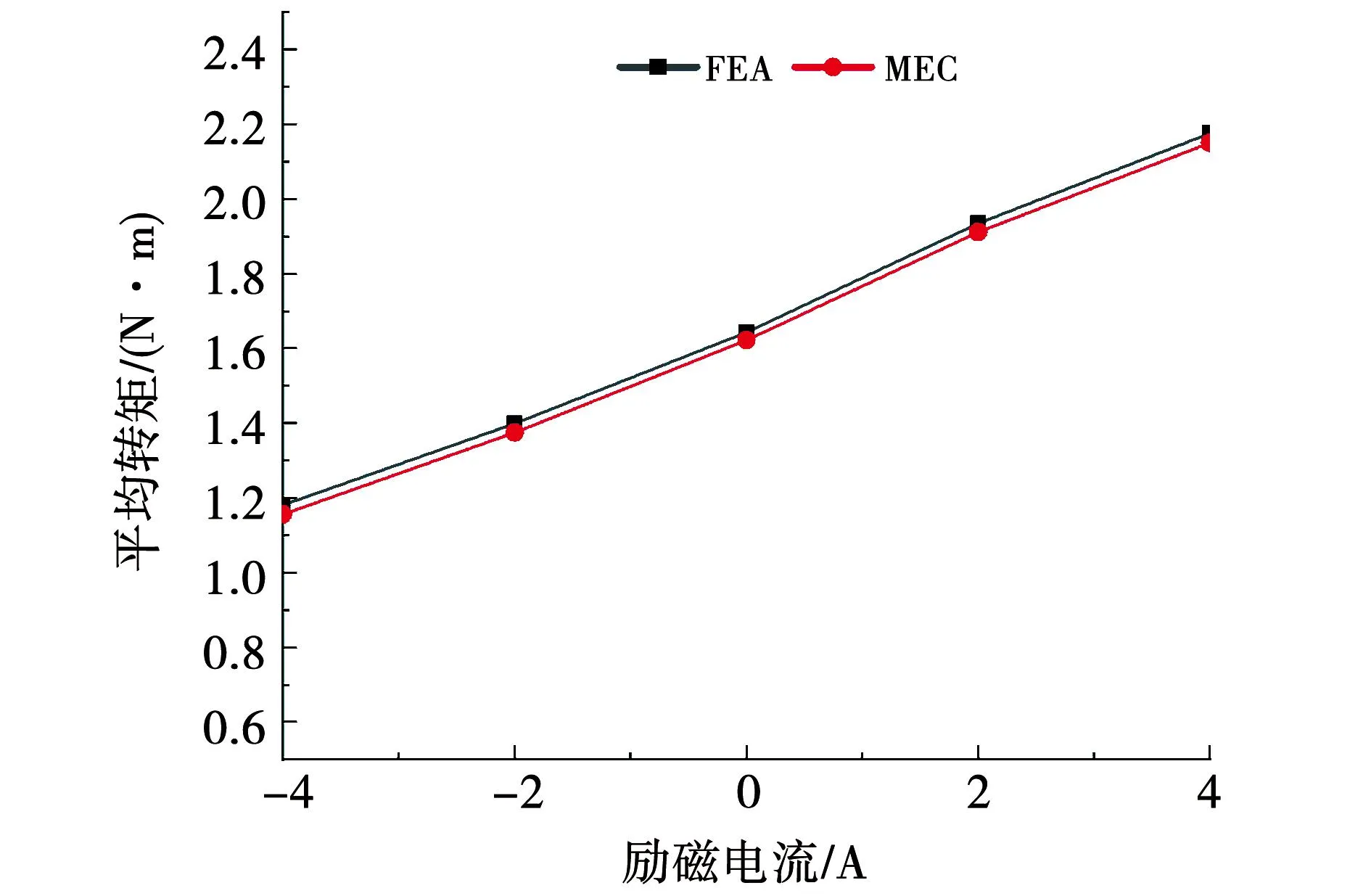
图18 不同励磁电流下平均转矩对比图Fig.18 Comparison of average torques at different excitation currents

由图18可知,电机电磁转矩随电励磁电流的增加近似线性增加,在电励磁电流为4A时,转矩提升了约32.39%。而传统永磁同步电机运行在低于额定转速时,其转矩为恒定值,随着转速的提高,输出功率线性增加。本文研究的模块化混合励磁电机在低速时通过增加电励磁电流if可以提升电机的输出功率,具有调节灵活方便的特点。

4.3 铁耗分析

电机的铁耗也是影响电机性能的重要因素,模块化定子混合励磁同步电机采用非晶合金材料代替传统的硅钢片材料,极大地降低了电机的铁心损耗,分别采用有限元与磁网络计算的方法对电机转速在1 000 r/min到4 000 r/min下使用硅钢片DW270与非晶合金两种材料的铁耗进行计算,计算公式为

(19)

其中:f为频率;kh为磁滞损耗系数;kc为涡流损耗系数;ke为附加损耗系数;Bm为磁密幅值。计算结果如图19所示。

图19 非晶合金与硅钢片铁耗对比图Fig.19 Comparison of iron consumption of amorphous alloy and silicon steel sheet

由图19可以看出磁网络解析计算与有限元结果相差不大,验证了三维磁网络模型的准确性;同时可以看出,电机采用非晶合金作为铁心材料时铁耗在1 000 r/min时由于频率较低且磁密不高,定子铁耗仅有0.32 W,在转速达到4 000 r/min时铁耗达到3.02 W。而采用DW270硅钢片在1 000 r/min时定子铁耗为非晶合金定子铁耗的8.7倍、2 000 r/min时为8.1倍、3 000 r/min时为7.7倍、4 000 r/min时为7.6倍。因此从铁耗的角度考虑,采用非晶合金可以极大地降低铁耗,提升电机效率。

5 结 论

本文以一台混合励磁同步电机为研究对象,在考虑电机局部饱和、漏磁、轴向磁路、电枢反应、转子转动等的基础上提出了一种三维磁网络解析模型,并对其进行了迭代求解计算。同时利用所搭建的三维磁网络模型分别计算分析了电机的气隙磁通密度、磁链、反电动势波形等特性,并通过有限元方法验证了所搭建磁网络的准确性。最后,对混合励磁同步电机的性能如调磁能力、电磁转矩、铁耗等进行了计算分析,得到了电机调磁能力良好、功率调节灵活以及铁耗低效率高的结论。该解析模型与有限元方法相比,在保证计算精度的前提下节约了大量时间,为分析此类混合励磁同步电机提供了新的思路。