福建省数字乡村发展水平评价及其提升对策*

吕舒婕 林 健,2

(1.福建农林大学计算机与信息学院,福建 福州 350002;2.福建农林大学农林大数据研究中心,福建 福州 350002)

1 概述

近年来,我国的整体发展呈现出一定的区域差异,这种不平衡的发展会导致资源更容易向发达的地方倾斜,如北上广深等特大城市引进大量高质量人才,长此以往,将会引发严重城乡数字鸿沟。党的十九大正式提出将乡村振兴作为全面建成小康社会的重大战略部署。实现乡村振兴,首当其冲应该关注如何更好地建设数字乡村。方迎君[1]根据乡村振兴的战略规划,从数字乡村现阶段发展状况出发,设计数字乡村建设评价指标体系;林帅君等[2]建立了一个涵盖产业、教育、治理、惠民、环境和交通等6个方面的未来乡村建设指标体系。此外,运用合适的方法确定指标体系权重也是数字乡村评价的研究重点之一。康妍[3]针对湖南省数字乡村实际建设状况,采用AHP法和优劣解距离法分别对评价指标的权重进行确定和实例分析;许敬辉等[4]以全国各省份的数字乡村相关数据为基础,通过因子分析法对数字乡村发展指标的重要程度进行测算区分;李欣悦等[5]从农村发展的局限性出发,采用变异系数法对各指标重要性进行计算;刘庆[6]以河南省为研究区域,采用熵权法计算出各数字乡村评价指标的权重,并进一步结合TOPSIS法对数字乡村发展水平进行测度;姜红波等[7]以Fuzzy-DANP法为媒介,对全国数字乡村各评价维度之间的相互作用关系进行分析与权重计算。

受限于专家的知识储备及客观存在的问题模糊性,所给出的判断信息往往是不确定的。但大部分数字乡村评价矩阵中的偏好表达均为精确的点值,忽略了决策信息本身的不确定性,且现有的数字乡村指标权重计算方法在与模糊评价模型结合运用时,并未对评价模型本身的性质即模型多解性进行深入研究,从而导致一些潜在的更优越的评价结果被遗漏。本研究为体现现实信息的不确定性,采用区间数对数字乡村发展建设水平进行评价,并将模型的多重最优解纳入评价考虑范围,完善了潜在最优解流失的不足。此外,还根据区间数特性构建了多重最优解的有效筛选算法,提出了数字乡村发展评价指标权重计算的新思路。

2 相关概念

对区间模糊判断矩阵相关的基本概念和一致性定义做出了简要解释,对后续筛选涉及的参与指标含义进行概括。设Z={z1,z2,...,zn}是一个备选方案的有限集,其中n≥2,zi表示第i个备选方案,则判断矩阵的相关概念如下所示。

①设T=(tij)n×n⊆Z×Z是一个模糊互补判断矩阵,w=(w1,w2,...,wn)T是模糊判断矩阵T=(tij)n×n的优先权重向量。若tij满足tij=0.5(wi-wj)+0.5,则称T是加性一致模糊互补判断矩阵[8]。

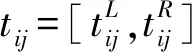
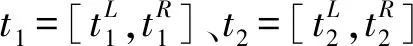
(1)

则称w为T的标准化优先权重向量。

(2)

⑤设T1=[tij(1)]n×n、T2=[tij(2)]n×n是方案集Z上的两个n阶矩阵,则两矩阵之间的相似度表示如下[13]:

(3)

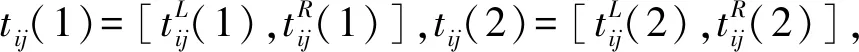
(4)

3 模型建立与多重最优解筛选

为实现乡村振兴,促进乡村数字化发展,大量专家利用各类方法对数字乡村发展评价各指标的重要性做出研究。其中,模糊测度是一种贴合实际的优越综合性评判媒介。但在利用模糊测度对属性指标之间的关系做出评判时,决策者通常倾向于给出一个包含具体含义的离散标度值,其范围在区间数中限定在[0.1,0.9],如tij=[0.3,0.4]表示备选方案zi相较于zj优劣程度在稍差与较差之间。相对应的,为尽量保证专家评价信息的流失水平处于最低限度,使调整后的信息能够更符合决策者的表达习惯,在信息矩阵一致性处理过程中的调整也应是离散的。此外,传统调整模型往往会忽略所计算出的最优解的多重性,根据调整方案的不同,在无形中可能隐藏了更优解的存在,导致最终计算结果并未实现最优。因此,考虑到专家评价下的各类乡村数字化评价指标的重要性需要更加全面且具有针对性地得到有效区分,本文挖掘模型最优解的潜在多重性,针对区间模糊判断矩阵的相关性质建立一个可考虑多重最优解的一致性离散调整和权重模型,并给出多重最优解的精炼算法。

3.1 建立区间模糊判断矩阵一致性调整模型

按照判断矩阵离散化调整的要求,首先在区间模糊严格加性一致性条件的基础上引入正负偏差的整数型变量,以0.1为单位对偏好信息进行离散调整,并限制调整后元素范围不超出[0.1,0.9]。其中,由于判断矩阵中元素之间的互补性,模型(M-1)及后续所涉及的模型均仅针对上三角矩阵元素进行调整和计算。其次,将模型目标设置为最小化元素调整量,且将权重的基本性质作为约束条件添加进模型中,模型设置输出多个解。最后,给出以下区间模糊判断矩阵一致性调整多重最优解模型(M-1):

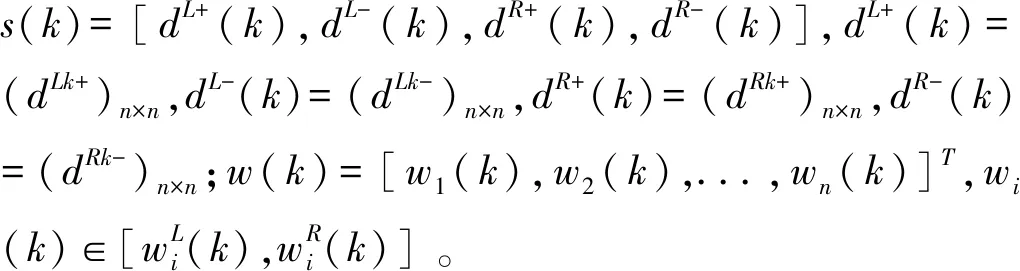
由于模型输出多个最优解,多重最优解筛选流程的设置就显得尤为重要,以下将对不同情况下的输出解筛选算法进行阐述。

3.2 多重最优解精炼算法

①输入多重最优解个数g(g≥0)及其对应的调整解组s={s(1),s(2),...,s(g)}和区间优先权重w={w(1),w(2),...w(g)},首先判断需要调整的g≥1是否具有多个最优解,若有则进入下一步,否则跳转到第4步。

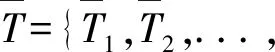
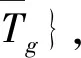
④输出唯一最优调整后矩阵Tk和区间优先权重 。

4 福建省数字乡村发展评价及分析

4.1 构建数字乡村发展指标体系

选定福建省福州市闽侯县上街镇为研究区域,对其整体数字乡村发展状况进行分析和评价。上街镇气候温暖湿润,有利于农业发展,内含19个行政村,且靠近福州高新区及大学城,无论是开展校地合作还是与高新技术企业合作都具有得天独厚的优势。同时,还具有丰富的文旅资源,与多条交通要道相通,为促进数字乡村项目高效建设和数字赋能乡村振兴提供了较为优越的条件。

根据“十四五”期间提出的乡村建设的六大内容,基于乡村振兴的总要求和数字乡村的建设内涵与宗旨,并结合上街镇高新企业众多、各类资源丰富的特点,遵循科学性、全面性及指导性三大原则[15],以实用性和普适性为目标,尊重以人为本的基本理念,从数字产业、数字科技、数字生活、数字基建和数字治理等5方面,对上街镇的数字乡村发展水平进行全面指标体系构建,共有5个一级指标,19个二级指标[1,15-16],如表1所示。

表1 数字乡村发展水平指标体系

续表

4.2 确定数字乡村发展指标权重

在实际应用中,部分指标的数据仅为一个较为模糊的范围,呈现出上下波动的趋势,利用区间数对其进行概括较为合理,相对应的,所计算的权重也应为区间形式,用以体现数据波动对指标重要性的影响。根据上文构建的数字乡村发展指标体系,利用所提出的多重最优解筛选方法,将模型(M-1)应用于指标重要性评价,并基于计算结果给出数字乡村发展体系内各指标的重要程度,以便后续进行针对性分析和建议。根据所构建的指标体系,邀请专家对闽侯县上街镇的数字乡村发展情况进行评判,各板块划分下指标评价的6个区间判断矩阵如下所示。

数字乡村评价体系内,b1～b5对应的19个二级指标c1～c19的区间判断矩阵Tb1、Tb2、Tb3、Tb4、Tb5分别为:

b1～b5等5个一级指标层的区间判断矩阵Tb为:

将以上6个判断矩阵分别代入模型(M-1)进行求解发现,Tb2为一致矩阵,无需进行调整,得到其对应区间优先权重W2={[0.2667,0.6667],[0.0667,0.6667],[0.0667,0.2667]};Tb5可得唯一解,经多重最优解算法筛选后,可直接输出其唯一解及对应区间优先权重W5={[0,0.4],[0.2,0.4],[0.2,0.6],[0.2,0.2];Tb1、Tb3、Tb4和Tb均输出多个最优解。因此,利用筛选算法对这4个矩阵的调整结果进行多重最优解筛选。

针对Tb1求解模型(M-1),计算得到s(1)、s(2)、s(3)、s(4)、s(5)、s(6)6个最优解和w(1)、w(2)、w(3)、w(4)、w(5)、w(6) 6个区间优先权重,最优调整量为2,因其有多个解,进入多重最优解筛选算法。6个调整解如下所示:

6个调整解的权重分别如下所示:

w(1)={[0.3333,0.7333],[0.1333,0.3333],[0.1333,0.3333]}

w(2)={[0.4667,0.6667],[0.0667,0.2667],[0.2667,0.2667]}

w(3)={[0.4667,0.6667],[0.0667,0.2667],[0.0667,0.2667]}

w(4)={[0.5333,0.7333],[0.1333,0.1333],[0.1333,0.3333]}

w(5)={[0.4,0.8],[0,0.4],[0.2,0.2]}

w(6)={[0.4667,0.6667],[0.0667,0.4667],[0.0667,0.2667]}

根据计算产生的6个区间权重,采用层级之间区间权重相乘的方式对单个二级指标的权重进行重新归一化,给出指标体系内各层级指标的重要性区间。计算得c1、c2、c33个数字产业指标的权重为wb1=([0,0.2667],[0,0.1067],[0,0.1067])T,c4、c5、c63个数字科技指标的权重为wb2=([0,0.2667],[0,0.2667],[0,0.1067])T,c7、c8、c9、c10、c115个数字生活指标的权重为wb3=([0.016,0.192],[0.016,0.512],[0.096,0.192],[0.016,0.192],[0.016,0.352])T,c12、c13、c14、c154个数字基建指标的权重为wb4=([0.02,0.2],[0.02,0.12],[0.02,0.28],[0.02,0.02])T,c16、c17、c18、c194个数字治理指标的权重为wb3=([0,0.08],[0,0],[0,0.12],[0,0.04])T。

计算结果表明,数字化服务生活普及度c8在指标体系中最为重要,其次为农村居民数字新兴产业就业程度c11,二者皆为概括乡村居民数字生活开展状况的指标。c7、c9、c10等3个指标也在指标体系中占有较高比重,符合数字乡村建设以人为本的中心理念。数字产业和数字科技的c1～c6、数字基建的c12～c14,以及数字治理的c18等10个指标的重要程度均在0～0.3,彼此相差较小,表明在上街镇未来的乡村振兴发展和数字乡村建设中,应当更加注重数字产业、数字科技和数字基建三个方面的共同建设,保持三者平衡共进。在细化到单个指标的情况下,应加强科技在农业发展上的应用,引进更多的专业技术人才,并继续保持乡村地区技术革新和发展,为经济增长带来的活跃力。从总体来看,数字治理下的几个指标占比较低,但这并不意味着乡村治理在数字乡村建设中无关紧要。为使乡村居民在生活中能够更加全面地享受到技术红利,高水平的基建是数字乡村建设的根本,良好的经济条件和科技的多样化应用是数字乡村未来长远发展的重要支撑,而推进乡村数字治理需要建立在前三者全方位发展的基础之上,因此,其建设紧迫度相对而言处于较低水平,乡村数字治理仍有较大发展空间。

4.3 结论与分析

数字乡村战略是我国深入实行乡村振兴,顺应新时代需求的前瞻性发展项目。本研究建立了区间判断矩阵下的严格加性一致离散调整和权重模型,并将最优解多重性应用在数字乡村评价建设中。需要特别指出的是,本文所提出的权重模型并不受到乡村多样性的限制,针对不同乡村建立不同指标体系时,其内指标的内容变动和数量增减均不影响所提模型及筛选算法的运用,其区别只在于所给出的判断矩阵的阶数变化。本文主要创新点如下:

①专家意见均按照0.1～0.9离散标度给出,此方式在评价数字乡村建设指标时也能够对各指标之间偏好信息的具体变动含义进行更直观的刻画,帮助决策者快速理解调整结果,从而提高反馈速度,令整体决策流程效率得到有效提高。

②所得到的区间模糊互补判断矩阵均由一个混合整数规划模型对其进行严格加性一致性调整和权重计算,且该模型在被运用于新的数字乡村评价指标体系权重计算中时,能够保证决策评价信息的内部逻辑性和计算合理性。

③最优解的多重性为数字乡村指标的权重求解问题提供了多种潜在的解决路径,决策柔性得到了大幅度提升,而多重最优解筛选算法依照信息量留存度最大的原则,使筛选得到的数字乡村指标权重结果能够保留最多的原始偏好信息,最大程度减少了调整过程中的信息扭曲与缺失。

5 建议

在农业产业发展层面,推动传统农业经济产业转型升级,引导电商、物联网和人工智能等新型数字化经济产业与农业生产和乡村服务业联合发展,开发增加农民的多渠道收入,实现农民数字化创收。

在农业科技层面,加大政府在新型农业科技研发和农业机械补贴的资金投入,提高智能农业机械在农民生产生活中的使用比例,并通过提高人才待遇吸引更多数字技术型专业人才安家落户,为数字乡村的进一步建设升级做好人才储备。

在农民生活层面,加强物流覆盖建设并提高在线数字化产品在乡村地区的普及率,对文化程度落后的农民开展针对性教育学习,提高农民对现代科技的认识度和应用参与率,从而实现广大乡村居民生活与数字化建设推进的时代衔接。

在农村基建层面,完善农村网络建设,加强乡村地区连通性,并推进新型科技与农业基建深度融合发展,统筹建设更多农业相关大数据管理平台和线下站点,为农业稳定繁荣创造良好发展环境。

在农村治理层面,提升政府的政务公开透明度和时效性,保障农民在乡村治理中的参与权。相关部门应加快出台数字乡村相关政策,为推进数字乡村建设提供政策支撑。