Support vector regression-based operational effectiveness evaluation approach to reconnaissance satellite system

HAN Chi, XIONG Wei, XIONG Minghui, and LIU Zhen

1.College of Aerospace Information, Space Engineering University, Beijing 101400, China; 2.Science and Technology on Complex Electronic System Simulation Laboratory, Space Engineering University, Beijing 101400, China

Abstract: As one of the most important part of weapon system of systems (WSoS), quantitative evaluation of reconnaissance satellite system (RSS) is indispensable during its construction and application.Aiming at the problem of nonlinear effectiveness evaluation under small sample conditions, we propose an evaluation method based on support vector regression (SVR) to effectively address the defects of traditional methods.Considering the performance of SVR is influenced by the penalty factor,kernel type, and other parameters deeply, the improved grey wolf optimizer (IGWO) is employed for parameter optimization.In the proposed IGWO algorithm, the opposition-based learning strategy is adopted to increase the probability of avoiding the local optima, the mutation operator is used to escape from premature convergence and differential convergence factors are applied to increase the rate of convergence.Numerical experiments of 14 test functions validate the applicability of IGWO algorithm dealing with global optimization.The index system and evaluation method are constructed based on the characteristics of RSS.To validate the proposed IGWO-SVR evaluation method, eight benchmark data sets and combat simulation are employed to estimate the evaluation accuracy, convergence performance and computational complexity.According to the experimental results, the proposed method outperforms several prediction based evaluation methods, verifies the superiority and effectiveness in RSS operational effectiveness evaluation.

Keywords: reconnaissance satellite system (RSS), support vector regression (SVR), gray wolf optimizer, opposition-based learning, parameter optimization, effectiveness evaluation.

1.Introduction

1.1 Background

Satellite reconnaissance refers to reconnaissance activities carried out in outer space using radar, radio receivers,and photoelectric sensors on satellite platforms.Considering the advantages of wide coverage, high security, and freedom from geographical conditions, reconnaissance satellite system (RSS) has outstanding strategic significance and civilian value in military requirements and civil applications.Therefore, it is indispensable to evaluate the operational effectiveness of RSS.

System effectiveness is defined as the ability of a system to meet the given quantitative characteristics and requirements under certain conditions.Effectiveness evaluation models have been studied in a wide variety of applications by using various methods, including analytic hierarchy process (AHP), analytical assessment,expert-based method, data envelopment analysis (DEA),and availability-dependability-capability (ADC) model.Li et al.[1] combined the fuzzy comprehensive evaluation method and AHP to evaluate the effectiveness of submarine cluster torpedo system, in which the complex non-linear relationship between weapon system and its influencing factors is difficult to describe.Xiao et al.[2]employed the DEA method to evaluate the effectiveness of family farms, the model achieved high accuracy but the quantity and quality of data are demanding, resulting limited scope of application.The ADC model is widely used in evaluation for its convenience.Shao et al.[3]employed the ADC model for low orbit communication satellite evaluation, in which the availability, dependability and capability matrices are difficult to obtain [4].Battle simulation assessment method evaluates the effectiveness of weapon system by collecting performance characteristics data [5].This method requires a large number of testing results as support, resulting in the restriction by factors such as test conditions and funds.

Based on the analysis above, traditional evaluation methods have many limitations.First, subjective influence cannot be avoided, leading to an impact on the accuracy of the assessment.Second, the efficiency of evaluation is low.For complex nonlinear system like RSS, classical evaluation methods are not competent.

1.2 Research motivation

Over the past decade, intelligence algorithms with high solving efficiency, such as neural network and support vector regression (SVR) have been widely employed in evaluation of complex weapon system-of-systems(WSoS) [6-8].Neural network models like back propagation neural network (BPNN) collect a large amount of data in the process of combat simulation.Li et al.[9]applied the model of efficiency prediction based on Elman neural networks to effectiveness prediction of command, control, communication, computer, intelligence, surveillance, reconnaissance (C4ISR) system.The fitting capability is relatively good but training stability is insufficient [10].For RSS studied in this paper, the number of evaluation object is so limited that it is difficult to obtain a large amount of usable historical data.To further improve the prediction accuracy of effectiveness with high-dimensional and noisy small samples, Ren et al.[11] proposed a method which extracts the common features on related domain data by taking advantages of the stacked denoising autoencoder.The accuracy is improved but the computational cost is also considerable.In comparison, SVR has fewer parameters and faster running speed on small samples.Cheng et al.[12] established a combat effectiveness evaluation model based on SVR, and completed the nonlinear mapping from evaluation indicators to operational effectiveness.However,analysis of evaluation object is not in-depth enough, the model setting and comparison are also relatively simple.Cui et al.[13] considered the problem of parameter selection in maritime weapons evaluation, but only employed grid search method, leading to poor effect of this model.The setting of parameters has large impact on accuracy and generalization performance of SVR, especially when dealing with high-dimensional data.To overcome this shortcoming, meta-heuristic algorithms, including population-based and individual-based algorithms, have achieved competitive result when dealing with SVR parameter optimization [14].The whale optimization algorithm (WOA) was applied to select SVR parameters for short-term power load forecasting [9].Sine cosine algorithm (SCA) was involved to optimize SVR parameters for the time series prediction [14].Particle swarm optimization (PSO) was employed in SVR for obtaining the optimal parameters in total organic carbon content prediction [15].The firefly algorithm (FA) was adopted in SVR parameters optimization for stock market price forecasting [16].The ant lion optimizer (ALO) was employed to optimize SVR parameters for on-line voltage stability assessment [17].The classic genetic algorithm (GA) was adopted to determine SVR parameters for forecasting bed load transport rates of three gravelbed rivers [18].The fruit fly optimization algorithm(FOA) was employed for predicting the number of vacant parkin spaces after a specific period of time [19].Most of the above researches started from a specific application field, which rarely discuss convergence performance and computational complexity.Motivated by these issues, this work attempts to optimize SVR parameters with good accuracy, convergence performance, and computational cost.The grey wolf optimization (GWO) algorithm is an excellent swarm intelligence method which has few parameters, and no derivation information is required in the initial search.Moreover, it is simple and scalable, and has a special ability to strike balance between exploration and exploitation during the search which leads to favourable convergence.As a result, the GWO algorithm is applied to SVR parameters optimization in this paper.

The GWO algorithm is proposed by Mirjalili et al.[20]in 2014.Compared with some proposed intelligent optimization algorithms, such as PSO, ALO, moth-flame optimization (MFO), SCA, WOA and multi-verse optimizer (MVO), GWO has advantages in global search ability, solution accuracy and convergence speed [21].However, standard GWO has many deficiencies.The diversity of population is usually poor due to the simple search mechanism, resulting in a high probability in premature convergence when dealing with multimodal problems.Meanwhile, the control parameter decreases linearly, leading to the restricted population distribution range.To overcome these deficiencies, many improvements have been employed in GWO to avoid premature convergence and improve the exploration ability [22-29].

In view of the defects of traditional evaluation methods and the GWO algorithm, the main purpose of this paper is to propose a prediction-based effectiveness evaluation method with SVR.Considering the imperfection of traditional SVR parameter selection, the improved GWO (IGWO) algorithm with three improvement strategies is applied to optimize the SVR parameters for efficient and accurate prediction of RSS.Finally, the established model is applied to the simulated RSS evaluation,and compared with several prediction-based evaluation model to verify the feasibility of the proposed approach.

1.3 Main contributions

The main contributions of this work are summarized as follows:

(i) SVR-based evaluation method is introduced to evaluate effectiveness of RSS.The proposed method not only avoids the influence of subjectivity, but also obtains a higher evaluation accuracy.

(ii) The IGWO algorithm with opposition-based learning strategy, mutation operator, and differential convergence factor is proposed to escape from local optima and relieve the premature convergence of the GWO algorithm.Numerical experiments of 14 test functions demonstrate the excellent convergence performance stability.

(iii) The performances of IGWO-SVR are superior to several prediction-based evaluation methods in both numerical experiments and operational evaluation.In view of the considerable prediction accuracy, stability,and computational complexity, this work provides an effective method for effectiveness evaluation.

The remainder of this paper is organized as follows.A review of SVR is provided in Section 2.Section 3 improves the GWO algorithm, benchmarks its performance with the test suite, and provides the main procedure for optimizing SVR parameters.Section 4 constructs the indicator system of RSS and provides the effectiveness evaluation framework based on IGWOSVR.Section 5 includes the case study of two experiments and discussion.Section 6 presents conclusions.

2.Survey of SVR

SVM was proposed by Vapnik in 1995 [30].It is a supervised learning algorithm for data analysis and pattern recognition based on statistical learning theory, which can realize data classification and regression analysis.SVR is an application of SVM to solve the regression problem, it has been widely used in many fields [31].The linchpin of SVR is to find the optimal classification surface and to minimize the distance between the training samples and the optimal classification surface [32].

SVR follows the principle of structural risk minimization, considering the range of confidence and empirical risk to achieve global optimization at the same time [33].In order to solve the non-linear problem of RSS effectiveness evaluation in this paper, SVR introduces a kernel function through appropriate non-linear transformations to map the non-linear problems in the low-dimensional space to the linear problems in the high-dimensional space.It reduces the problem of finding the optimal hyperplane of linear regression in the feature space to solving the convex programming problem and finding the global optimal solution [34].The principle of SVR can be briefly described as follows.

Assume that the training set is given asT={(xi,yi)|i=1,2,···,n} , wherexi∈X=Rnindicates theith element of input inn-dimensional space andyi∈Y=R indicates the actual value corresponding toxi.In the case of nonlinearity, kernel function κxi,xj=φ(xi)×φxjis introduced to map the input samples from the original space to the high-dimensional feature space for linear regression, thereby establishing a linear regression model in high-dimensional feature space.The regression function after transformation can be shown as

wheref(·) denotes regression function; ω is the weight vector; φ(·) denotes non-linear mapping function of kernel space for extracting the character from the original space;bdenotes the bias.

In order to maintain good sparsity in SVR, the ε-insensitive loss function is introduced to minimize the structure risk, where ε denotes the allowable error value of the regression function.The ε-insensitive loss function is defined as

A certain margin of difference is allowed between the actual and predictive value.When the difference is less than ε, the loss is zero.As the value of ε becomes larger,the sensitive band width increases while the model complexity decreases.However, this may lead to the occurrence of “under-learning”.In contrast, if ε is too small, it may cause the problem of “over-learning” [35].

SVR can be described as the solution to ω andb, minimizing //ω//2/2 on the premise of satisfying ε.With the introductionof slack variables ξiand, SVR is transformed into a minimization problem of seeking optimization objective function, which can be shown as

whereCis a constant known as the penalty factor andrepresent the difference between target value and estimated value.

Introducing the Lagrange function, the above problem is transformed into its dual form as

where α1andare Lagrangian operators.Define training sample that satisfiesas support vector.Solve (4) to get the saddle point of the convex function,and the regression function is

whereNdenotes the number of support vectors.The kernel function adopts a radial basis function with strong generalization ability.

where the radius parameter σ of the kernel function has a great influence on the learning performance of SVR.The choice of the appropriate radius parameter is a key issue in parameter selection of radial basis function (RBF) core SVR model.The structure of SVR is shown in Fig.1.The optimization of SVR is a typical multi-parameter optimization problem, in which it is of vital importance of obtaining balance between exploration and exploitation.The special capability to strike the right balance between exploration and exploitation is precisely the advantage of GWO, which is developed to solve the global optimization problem.Therefore, GWO is selected to optimize SVR in this paper.

3.IGWO-based SVR parameters optimization

3.1 Standard GWO algorithm

GWO is a biological heuristic optimization method derived from simulating the social hierarchy and hunting mechanism of gray wolf in nature, which has been proven to have a more reasonable global optimal search mechanism and suitable for processing parameter optimization problems [36].Also it has very few parameters, and no derivation information is required in the initial search,thus GWO is used to optimize SVR.In GWO algorithm,the swarm is divided into four groups according to the degree of fitness from high to low:α,β,δ,ω, whereα,β,andδare the leadership (the optimal solution) to guide other wolves to search for the target.The remaining (candidate solutions) update their positions aroundα,β, orδ.The optimization process of GWO is the position update process ofα,β,δ, andω[37].

The mathematical model of the gray wolf algorithm includes three steps.

Step 1 Encircling behavior.According to the surrounding mechanism of wolves in nature, the behavior of hunting prey is defined as

Equation (7) represents the distance between the prey and the gray wolf.Equation (8) denotes the position update formula of the gray wolf.tis the current iteration number,Xt(f) is the position of the prey, andX(i) is the position of the gray wolf.LandEare coefficient vectors:

where convergence factoradecreases linearly from 2 to 0 as the number of iterations increases.|r1| and |r2| are randomly distributed in the interval [0, 1].

Step 2 Hunting behavior.During the hunting process, the three-level individuals ofα,β, andδlead to finding the direction and gradually approaching the prey.The mathematical model of the individual tracking the prey is described as

whereDα,Dβ, andDδrepresent distances between α, β, and δ , respectively.Xα,Xβ, andXδrepresent the current positions of α , β, and δ , respectively.E1,E2, andE2are random vectors.Xdenotes the individualωposition at the current moment.

Equation (12) describes the direction and step size of theωadvancing to α, β, and δ.Equation (13) determines the final position ofω.

Step 3 Attacking behavior.Asadecreases linearly with the approach to prey, the corresponding |L| also changes within [-a,a].When |L|<1, the algorithm converges to obtain the position of the prey.

3.2 The proposed IGWO method

3.2.1 Opposition based learning strategy

For most evolutionary methods, individuals may fall into a local optimal value when it comes to most evolutionary algorithms.Hence, finding some methods to explore the entire solution space as much as possible is indispensable[38].To enlarge the hunting range of the swarm and avoid problem of local optima, opposition-based learning(OBL) strategy has been applied to improve the performance of evolutionary methods by comparing the performance of both the opposite solution as well as its original solution [39].The basic mechanism of OBL is evaluating optimal solution obtained in the current search as well as solutions in the opposite direction to the optimal solution at the same time, as shown in Fig.2.Therefore, if the current solution is local optimal, then the algorithm successfully jumps out of it, which will increase the probability of finding better solutions.As a result, the global exploitation and local exploration of the population can be effectively enhanced.The OBL strategy can be described as

3.2.2 Mutation operator

The mutation operator is proposed to improve the population diversity [40], as shown in Fig.3.

Fig.3 Mutation operator

The main idea of mutation operator is that the global best-known solution found by the swarm can provide multiple search directions for the agents, while the mutation operator can increase the swarm diversity.The basic mechanism is maintaining elite individuals and enhancing the distribution range of solutions in the space at the same time.In order to achieve this goal, firstly, the offspring swarms generated by the GWO method is merged with swarms generated by the OBL strategy, thus a hybrid swarm is formed, which has 2mindividuals.In the hybrid swarm, all individuals will be sorted according to t he fitness values.The first halfmindividuals are reserved as the new swarm.The toppindividuals with the best fitness values will be selected as the next generation, while the remainingm-pindividuals will be applied to generate mutants by (16).

In this way, the diversity of the swarm is enhanced while the elite individuals are maintained at the same time.

3.2.3 Convergence factor In standard GWO, the balance between exploration and development capabilities is controlled by parametera,which decreases linearly over [0,2].However, in actual optimization problems, due to the extremely complex search process of the algorithm, it is difficult for the linear decreasing strategy of the control parameterato adapt to the actual situation of the search.Dynamically changeable functions ofamust be used instead of identical linear function.The mechanism for differential convergence functions is that search intensity should be determined by dominance.The exploration intensity of α,as a commander, is the lowest among α,β,δ, whereas it is the highest for δ.According to this phenomenon, convergence function ofashould be compatible with dominancy priority.Fig.4 confirms that the proposed functions completely pay attention to the priority such that functionaδresults in higher values thanaαandaβ;aαis the lowest one.Hence, the decreasing functions foraofα,β, andδare described as follows:

whereamaxandamindenote the upper bound and lower bound ofa, respectively.iis the current iteration andimaxis the maximum number of iteration.ηα,ηδare the growth factors of α and δ , respectively.The values of ηα,ηδare 2 and 3, respectively.

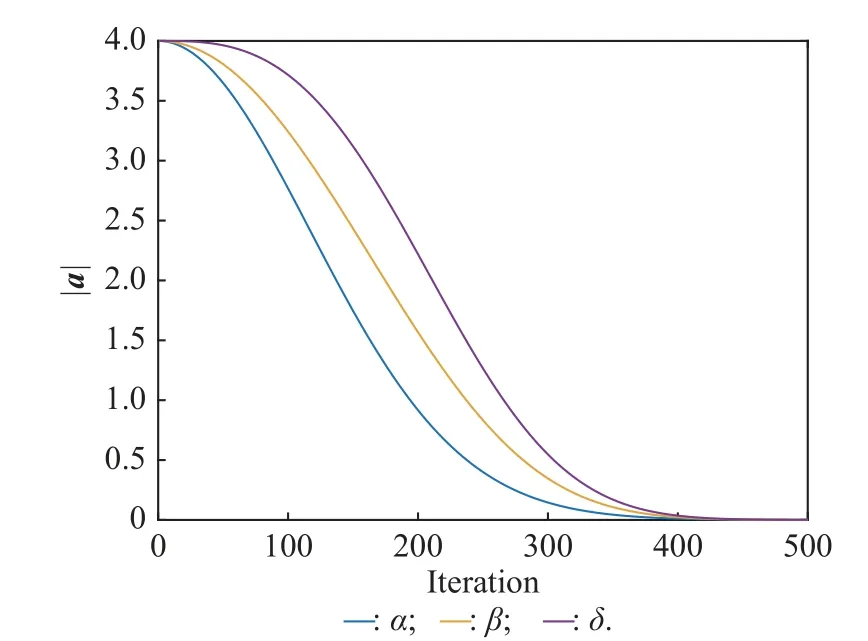
Fig.4 Comparison of decreasing functions ( aα,aβ , and aδ) for IGWO

The value of the three functions over iterations are shown in Fig.4.As the commander, the exploration of α is the lowest.Based on this finding, function ofashould compatible with dominancy priority, which means that functionathas higher value thanaαandaβ, whileaαis the lowest.In this way,aα,aβ, andaδare dynamically changed instead of adopting identical linear functions.

3.2.4 Execution procedure of IGWO

The pseudo code of the proposed IGWO algorithm with the above three strategies is presented as Algorithm 1.

Algorithm 1 Framework of IGWO Input: maximal number of generations , swarm size N.Xα imax Output: the best search agent

1: /* Initialize a, L and E */2: Calculate the fitness of each search agent Xα 3: ← the best search agent Xβ 4: ← the second best search agent Xδ 5: ← the third best search agent i imax 6: While <7: for each search agent 8: Update the position of the current search agent with (14) and (15)9: end for aα aβ aδ 10: Update , , , L and E 11: Generate the new swarm with (16)12: Calculate the fitness of all search agents Xα Xβ Xδ 13: Update , , and 14: i = i + 1 15: End while Xα 16: Return

3.2.5 Performance analysis

Multiple comparison methods are applied in this work for testing the performance of improvements adopted in the proposed IGWO algorithm.The algorithms in comparison and the corresponding descriptions are shown in Table 1.

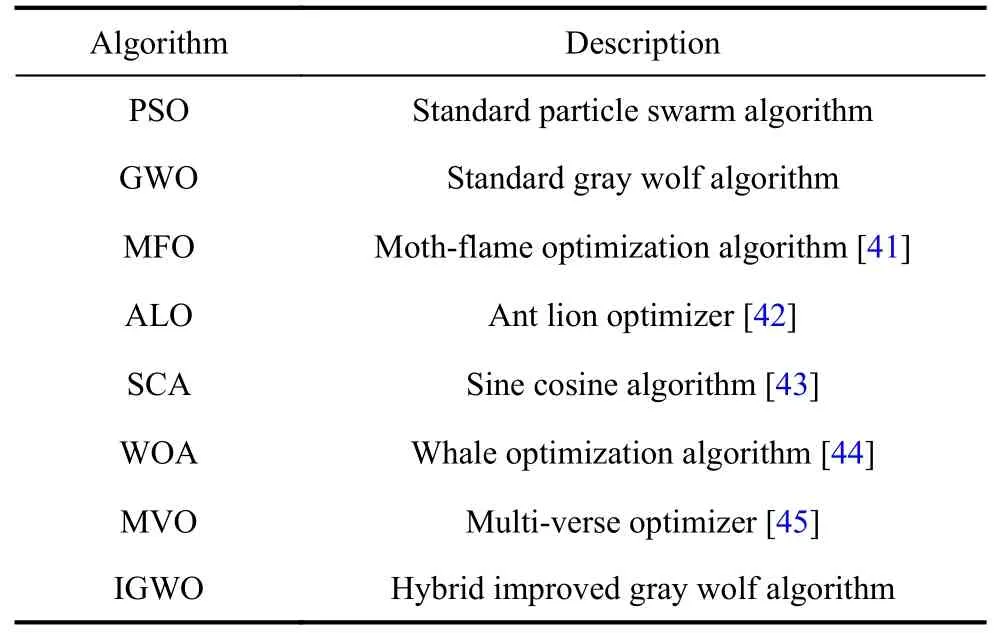
Table 1 Comparison algorithm and description

To ensure the reliability of the results, all comparison algorithms uniformly set the maximum population size to 30 and the maximum number of iterations to 500.

To evaluate the proposed IGWO, 14 test functions are chosen to be optimized, including the unimodal functions(f1-f7) with one global optimum, multimodal functions(f8-f11) with multiple optimal solutions and fixeddimensional multimodal functions (f12-f14).The test functions are widely used to assess the performance of state-of-the-art algorithms [28].The details of the 14 test functions are shown in Table 2.For each test function,thirty runs are conducted independently to reduce the negative effect of randomness.Table 3 shows the results for all test functions.The accuracy and stability of the algorithms are described by the average and standard deviation (Std.) of 30 independent results respectively.

According to Table 3, in most test functions, the proposed method has significantly better performance than the standard GWO algorithm.For example, the global optimal objective values of several functions (f5,f9, andf11) are obtained by the proposed IGWO algorithm triumphantly while the other methods fail to make it, which demonstrates the better performance of IGWO when it comes to multimodal functions.In the fixed-dimensional multimodal test functions (f12-f14), IGWO has the best standard deviation among these methods.Furthermore,the running time of the proposed IGWO is less than 0.5 s,demonstrating its high execution efficiency.It should be noted that the running time of PSO and MVO is shorter than the proposed IGWO inf1,f2, andf4with a slight difference.The improvement strategies introduced in the IGWO algorithm (opposition-based learning strategy and mutation operator) have brought a relatively greater computational complexity.When dealing with simpler optimization problems, there is no need for greater computational complexity, which leads to a slight advantage in the running time of GWO and PSO algorithms in some cases.In summary, IGWO has advantages in most test functions.Compared with GWO and other algorithms,the proposed IGWO algorithm is capable of seeking approximate optimal solutions efficiently for different functions.

Fig.5 demonstrates the convergence trajectories of IGWO v.s.standard GWO, PSO, MFO, ALO, SCA,WOA, and MVO algorithms.According to Fig.5, IGWO is able to seek out solutions quickly compared with other methods in most functions.The optimization of PSO and SCA is relatively poor.Meanwhile, the convergence trajectories of GWO, and IGWO algorithm flatten out when the number of iteration beneath 500 inf1,f2, andf4, while the modified algorithm continues rapid convergence.Inf3, WOA, GWO, and IGWO have similar performance,while IGWO is slightly superior in accuracy.Inf7, iterative curves of algorithms in comparison are stepped,becausef7has a large number of local optima.It can be seen that MVO, PSO, MFO, and ALO fall into local optima.Although IGWO, MVO, SCA, and WOA converge at a similar speed, the accuracy of IGWO is the best.In multimodal functionsf9,f10, andf11, IGWO converges to the global optimum solution as the iteration is about 200, which is faster than the algorithms in comparison.The experimental results verify the modified strategies employed are capable of enhancing convergence performance of the standard GWO algorithm effectively with convergence rate and the avoidance of premature convergence.

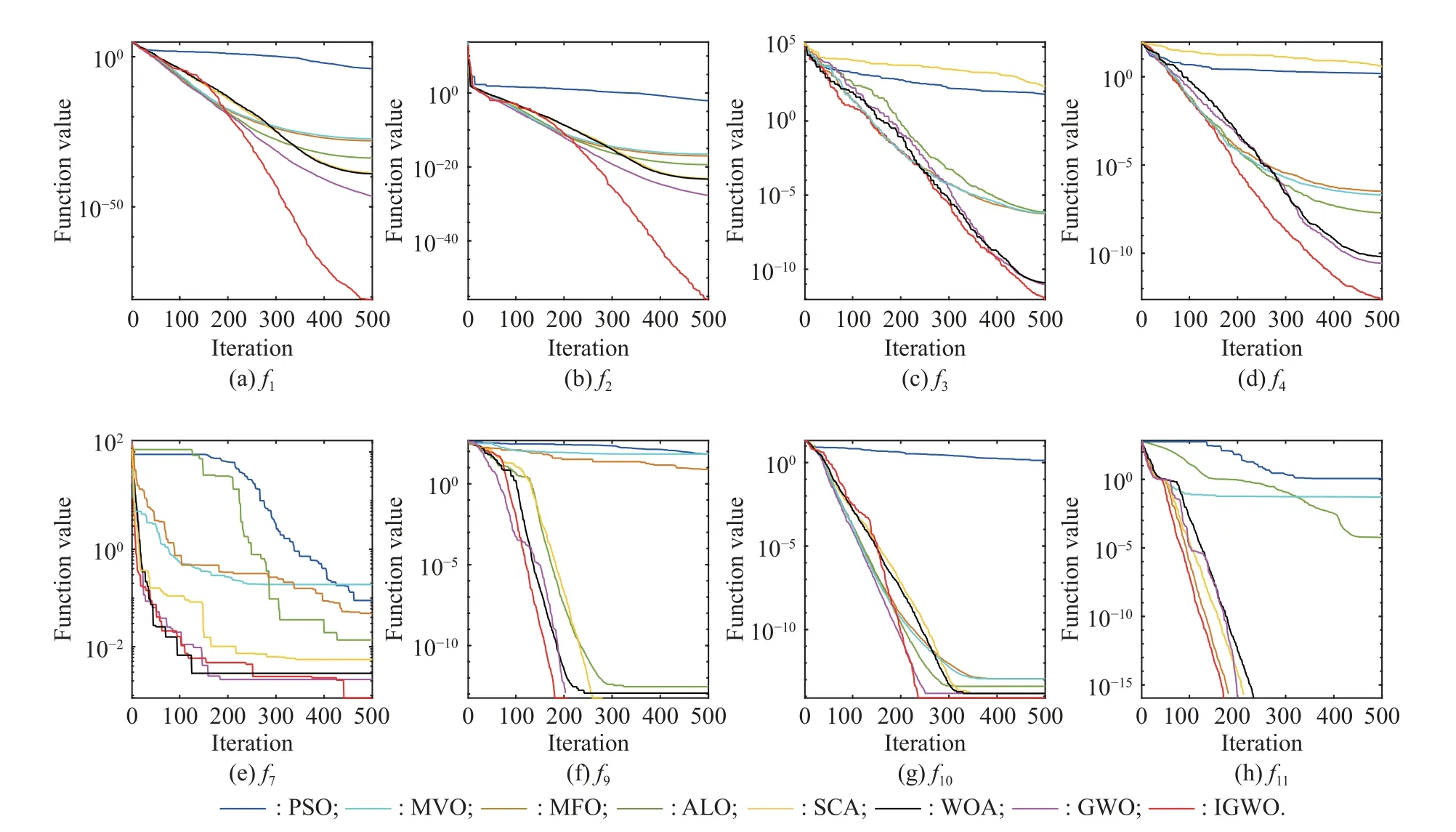
Fig.5 Convergence trajectories of six algorithms for eight test functions with 30 variables

3.3 IGWO-based SVR parameters determination

In this subsection, the IGWO-SVR approach is proposed.Two issues are mainly discussed.(i) It is necessary to determine the overall representation of SVR parameters[46].The methods proposed against these two issues in the proposed IGWO-SVR are discussed.The populationX={X1,X2,···,Xn} consists ofXi(the individuals), wherendenotes number of individuals.Xiis determined by SVR parameters.The three main parameters of SVR, penalty factorC, Gauss kernel function σ and insensitive loss function ε are selected to be optimized.The individualXi={C,σ,ε}.(ii) The choice of a suitable evaluation approach is necessary.In most regression issues, mean squared error (MSE) is usually chosen as the indicator.In this study, MSE is selected as the fitness function.

The overall framework of the proposed IGWO-SVR method is illustrated as shown in Fig.6.

Fig.6 Schematic diagram of the IGWO-SVR method

Step 1 Initialize the gray wolf population position with the OBL strategy according to (14).Confirm the lower and upper limits ofXi={C,σ,ε} for forming the limit sets lb and ub, respectively.The number of population is marked asM.The maximum of iterations is Max_Iter.The loop countIis set to 1.

Step 2 Divide the samples into training set and testing set.

Step 3 The supervised learning is conducted with SVR with training set andXfor obtaining corresponding models.

Step 4 Evaluate the performance of SVR for MSE with the training models.

Step 5 Classify individuals in accordance with fitness value.Individuals with the best fitnessα,β, andδare retained, and the remaining individuals are updated according to (11)-(13).Thus obtain the current optimum SVR parameter set.

Step 6 IfI> M ax_Iter , jump to Step 7.Otherwise,I=I+ 1, jump to Step 3.

Step 7 OutputXoptas the best parameter of SVR.

4.Construction of effectiveness evaluation model

4.1 Effectiveness evaluation indicator system construction

RSS undertakes the task of providing intelligence and information support for command organizations at all levels, combat troops, and main combat weapons.To evaluate its effectiveness, a reasonable indicator system is a prerequisite.However, the effectiveness and connotation measurement framework of RSS are still unclear.In order to quantify the operational effectiveness of RSS in the combat system to guide the development of equipment construction, many research have been conducted on the index system of RSS [47-51].The selection of underlying indicators of RSS needs to meet the general principles of objectivity, timeliness, measurability, completeness, and consistency.Meanwhile, due to the spatiotemporal dynamic characteristics of RSS, the satellite applications are constrained by satellite system orbits and combat units, resulting in vagueness and uncertainty of RSS’s operational effectiveness.Therefore, the establishment of the indicator system for RSS requires continuous iteration.

The main steps of the iteration are as follows.(i) Establish a workable evaluation indicator architecture.(ii) After the construction of preliminary evaluation indicator system structure through practice testing, the business authorities, experts and technical personnel are constantly solicited for suggestions to improve the construction.(iii) The effectiveness evaluation indicator system is finally obtained through continuous practice and repeated iteration.The process is shown in Fig.7.

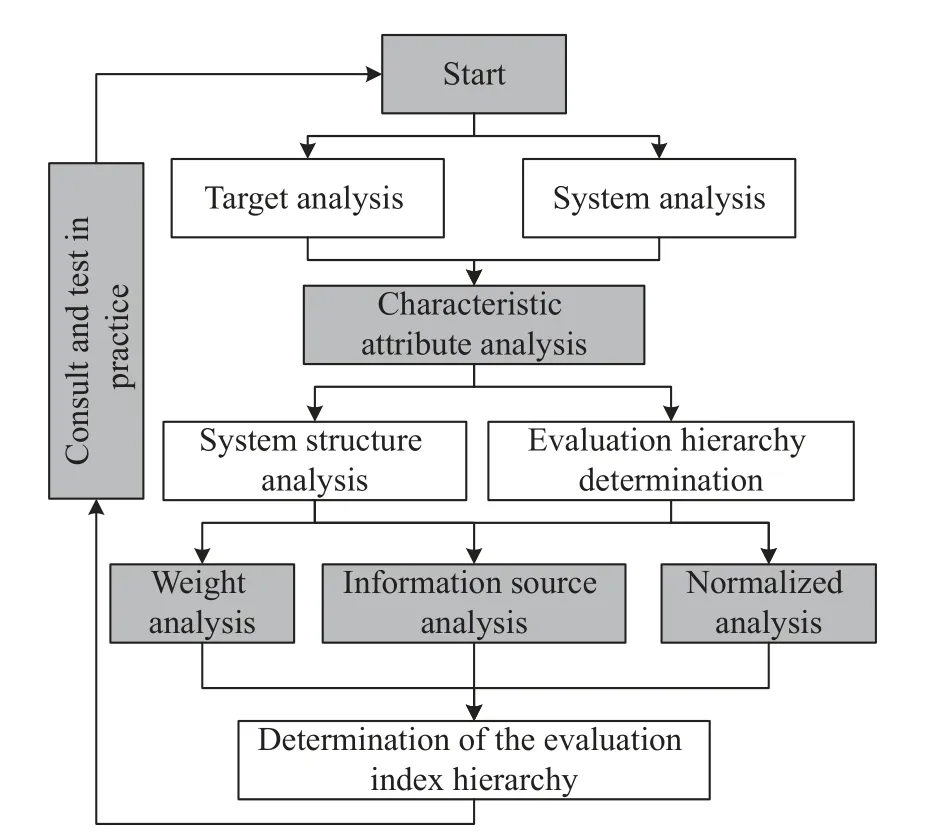
Fig.7 Process of indicator system establishment

Through the process shown in Fig.7, the effectiveness evaluation index system of RSS has been established.Four operational effectiveness indicators: signal reconnaissance capability, imaging reconnaissance capability,information transmission capability, and reconnaissance information processing capability are established, respectively.Each of the above indicators can be decomposed into multiple quantifiable individual performance indicators.Finally, a layered decomposition indicator system for evaluating the effectiveness of RSS is obtained, as shown in Fig.8.

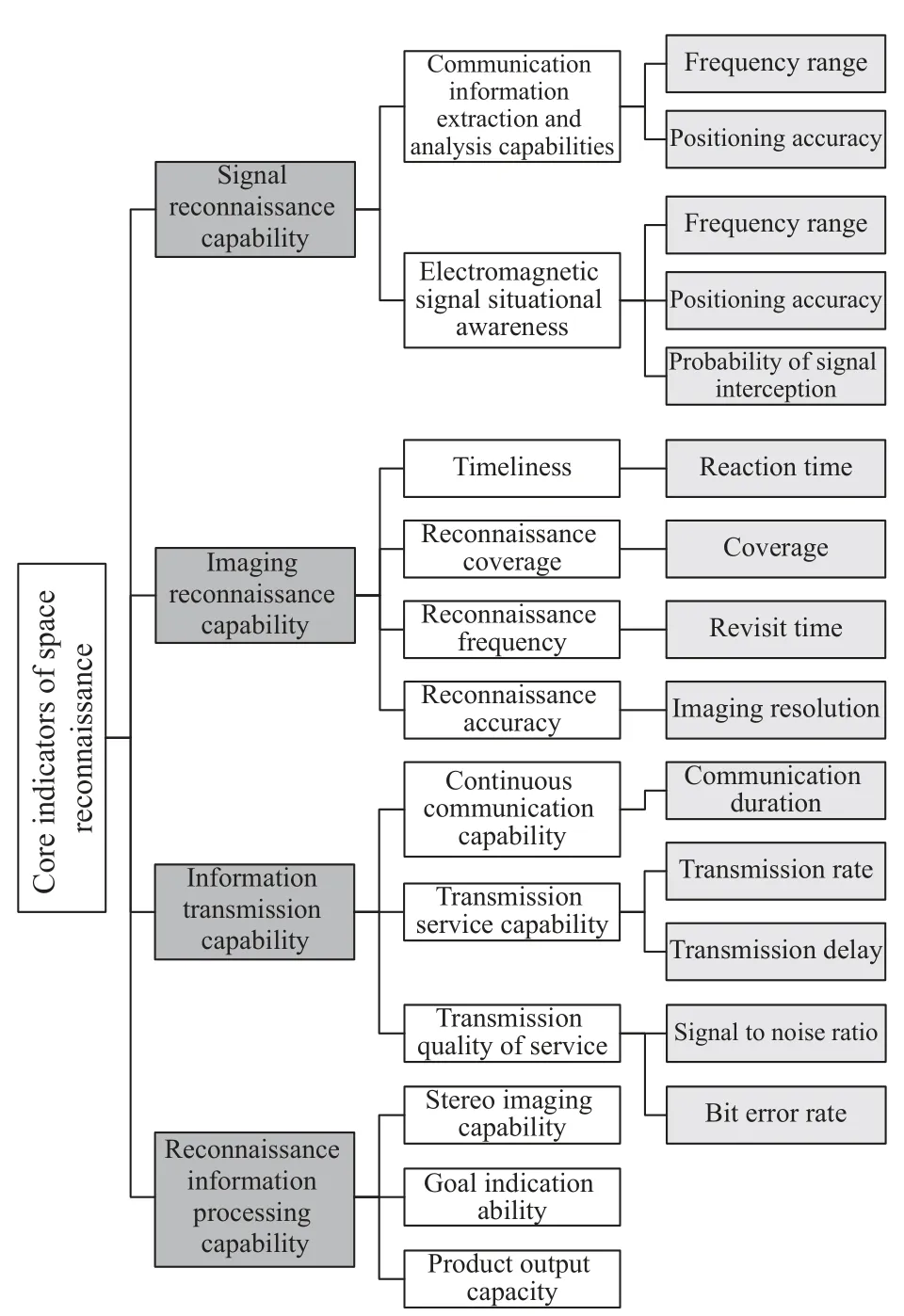
Fig.8 Operational effectiveness evaluation indicator system of RSS

Based on the specific application of the RSS and availability of data, a total of six indicators including coverage rate, revisit time, communication duration, response time, reconnaissance frequency, and transmission delay are determined as data characteristics.Each indicator is defined as follows: (i) Coverage: the ratio of the target area covered by the space reconnaissance system to the total target area at a certain moment.(ii) Revisit time: the revisit time measures the interval between when the area is not covered.(iii) Communication duration: the duration of a single communication.(iv) Response time: the time from a point when a coverage request is made to when it is under coverage.(v) Reconnaissance frequency:the number of times the area can be covered by the space reconnaissance system in a unit time length.(vi) Transmission delay: the time required for reconnaissance data to be transmitted from the satellite constellation to the ground terminal.

4.2 Effectiveness evaluation based on TOPSIS

On the basis of the constructed indicator system, in order to verify the validity of the IGWO-SVR model, the study adopts the technique for order preference by similarity to an ideal solution (TOPSIS) method for evaluation.The TOPSIS method of multi-attribute decision-making is constructed based on the aerospace RSS index system.The entropy weight method is adopted to obtain the weight of each indicator, calculating the closeness,obtaining the comprehensive value of each indicator [52].The procedure of effectiveness evaluation with the TOPSIS method is shown as follows.

4.3 Effectiveness evaluation model based on IGWO-SVR

The main ideas of effectiveness evaluation and machine learning are similar.They both establish the appropriate models to evaluate or predict goals under the premise of determining the evaluation goals.Based on this, the essence of the effectiveness evaluation process is to solve a multi-objective input nonlinear equation, which can be described by the following model:

The IGWO-SVR based effectiveness evaluation model is shown in Fig.9.Firstly, according to the aerospace reconnaissance equipment effectiveness evaluation index system, a data set is obtained.Takexij, thejth index of theith group of data, as the input, while the actual evaluation valueYi(i=1,2,···,n)is takenastheoutput.Theprocessed indexdatais dividedintotrainingsetandtesting set.The training set is used to train the model to obtain mapping relationship between effectiveness value and indicators.The accuracy and effectiveness of the model can be determined by comparing the output evaluation value and the theoretical value.

Fig.9 Flowchart of the operational effectiveness evaluation of RSS based on the IGWO-SVR model

5.Case study

The experimental conditions include (i) Intel®Core™i7-8750H CPU@2.21 GHz, 32 GB RAM, windows 10 64-bit operating system; (ii) Matlab R2016b and STK 11.2; (iii) Libsvm toolkit for Matlab; (iv) data sets,which are obtained from combat case simulation and the university of california at irvine (UCI) machine learning repository, respectively.The main features of UCI data sets are shown in Table 4.Considering the speed of operation, all data sets are normalized in the range of[0,1].Case study consists of two experiments.The first one is adopted to evaluate the accuracy and stability of the prediction, as well as the computational complexity of the proposed method, which is conducted with University of California, Irvine machine learning repository.The second experiment verifies the feasibility of the proposed IGWO-SVR model in RSS effectiveness evaluation with data obtained from simulation.

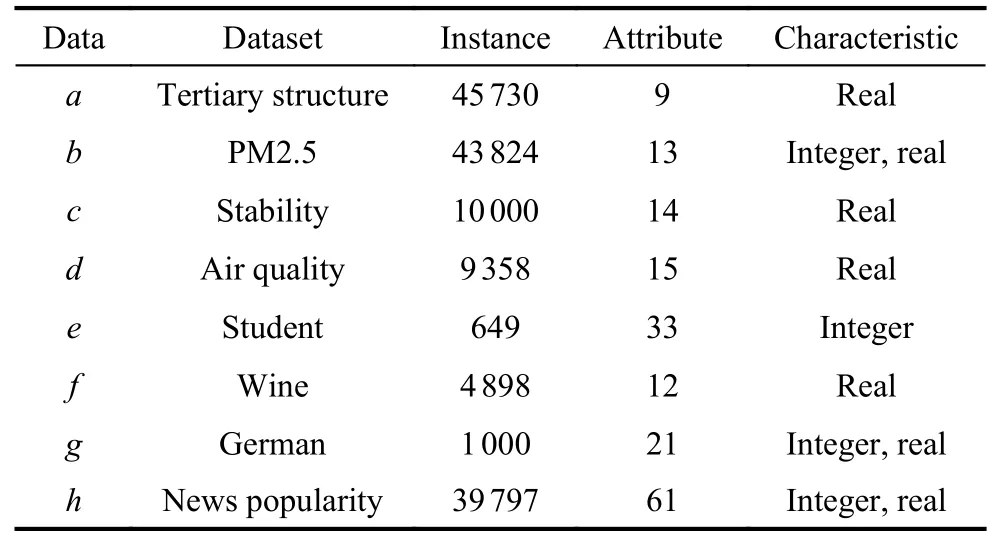
Table 4 Basic information of eight training data sets

5.1 Experiment I

In Experiment I, the proposed IGWO-SVR method is compared with SVR, GWO-SVR and BPNN based on the data sets from UCI machine learning repository, in order to evaluate prediction accuracy and computational cost.The initial parameter settings of these methods are shown in Table 5.Training data accounts for 80%, and the remaining 20% is used as testing data.According to the training and testing data, the optimum prediction accuracy is acquired through procedures in Section 3.For each method the procedure repeats twenty times under the same conditions.The average and standard deviation of 20 accuracies are shown in Table 6.The box-plot of prediction accuracies is shown in Fig.10.The whiskers denote the maximum and minimum MSE, the box indicates quartiles and the horizontal line denotes mean of MSE.In datasetsb,e,f, andh, the proposed approach obtains the minimum MSE against BPNN, SVR and GWO-SVR.Meanwhile, the distribution of MSE is more concentrated, verifying the stability of the proposed approach.The computational cost of these methods is concerned with the amount of instances and attributes.As a result, accurate calculation of complexity is usually a hard work.In this experiment, the average running time on the same criteria is calculated, as shown in Table 7.The unit of data is s.According to Table 7, IGWO-SVR acquires the minimum computational cost when it comes to datasetsb,e,f, andh.For rest of datasets, the consequence of IGWO-SVR is also competitive.

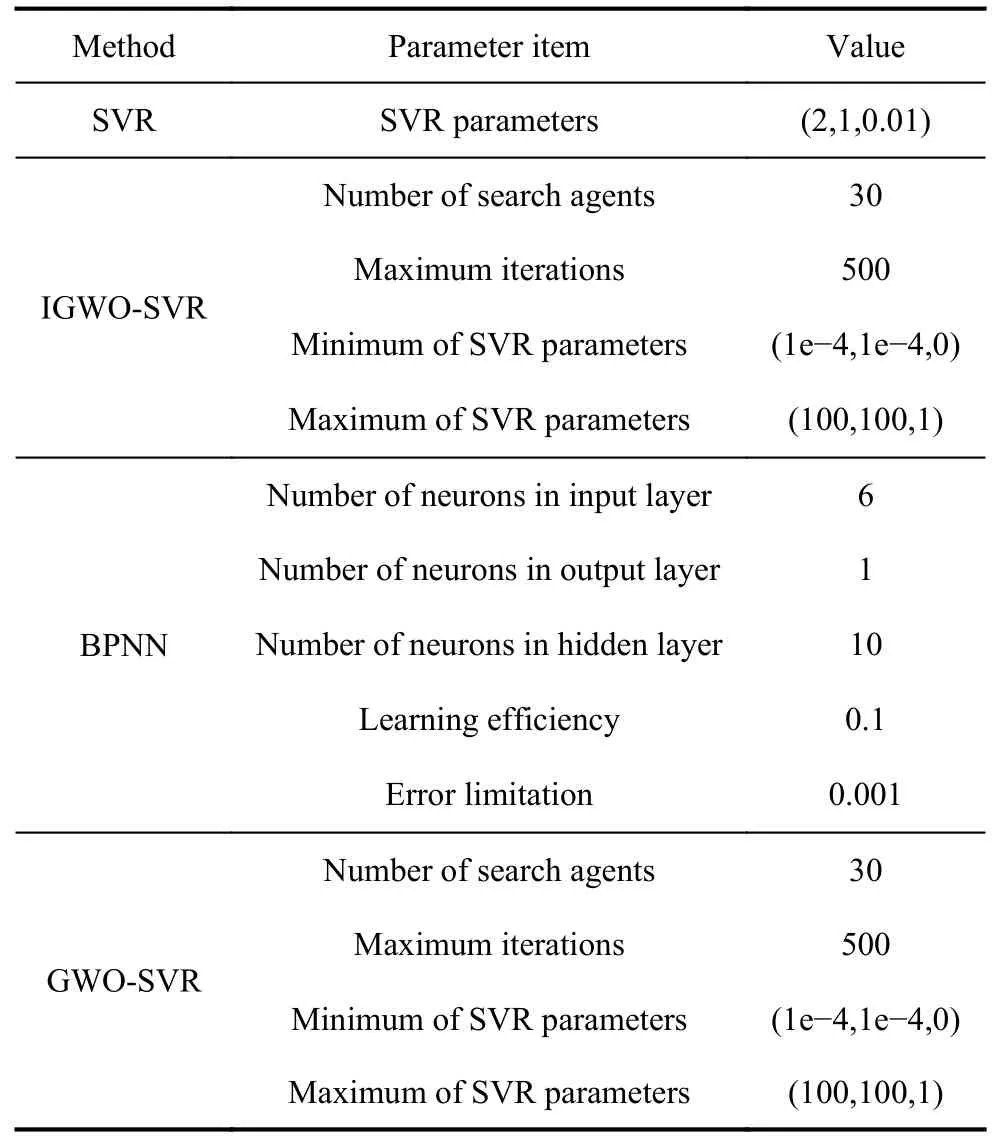
Table 5 Initial parameter setting of IGWO-SVR and other methods

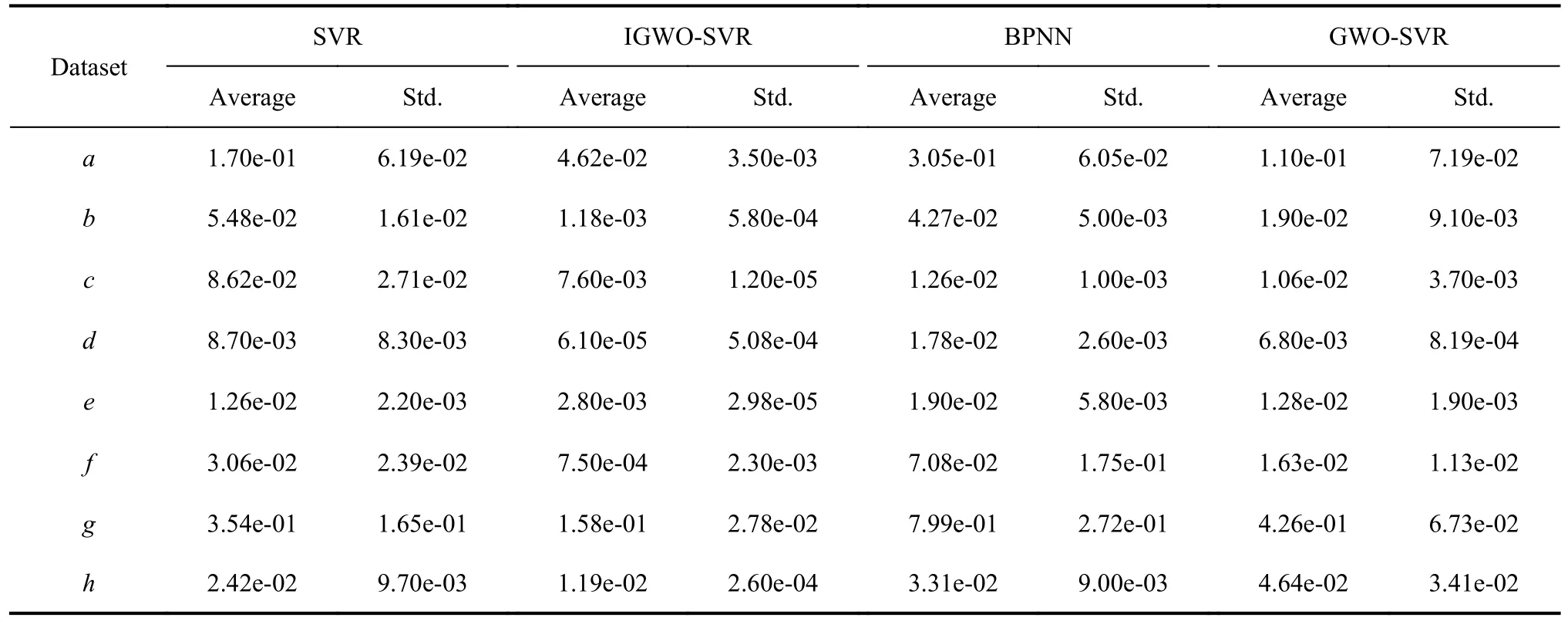
Table 6 Prediction accuracy results for all data of each method

Fig.10 Box-plot charts of MSE for IGWO-SVR and rest of methods based on eight datasets

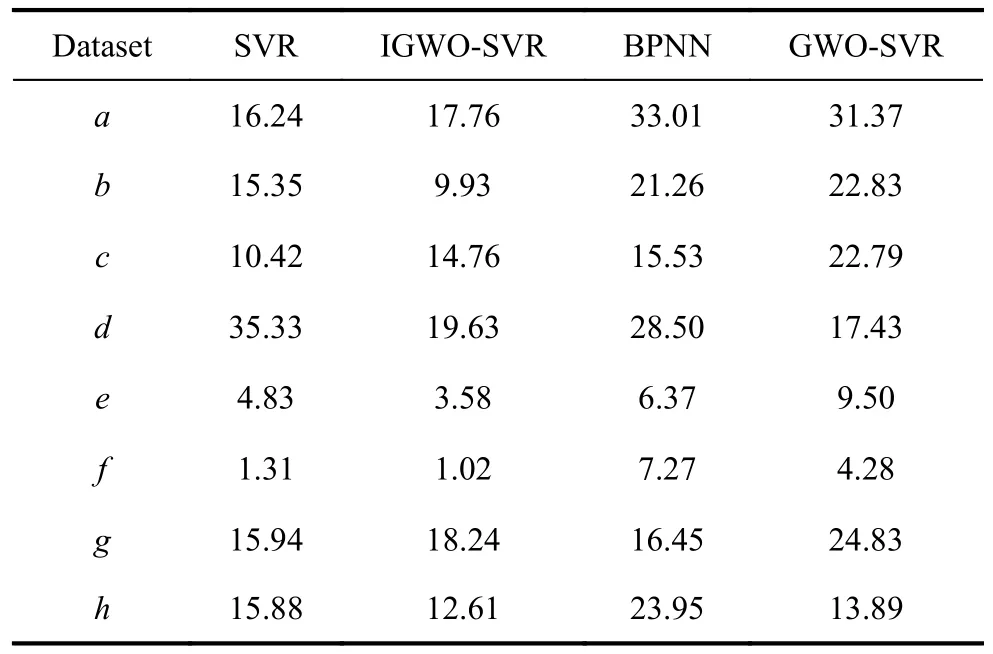
Table 7 Average running time of IGWO-SVR against other methods based on eight datasets

Furthermore, Wilcoxon’s test is conducted to verify the statistical significance of differences in computation results.Wilcoxon’s test is a nonparametric hypothesis testing method, usually employed to determine whether data come from the same distribution.First, suppose that the prediction accuracy of IGWO-SVR is significantly different from the accuracy of GWO-SVR, BPNN, and SVR.Let the significance level α=5%.ThePvalue obtained by Wilcoxon’s test of the IGWO-SVR method against rest of the methods are displayed in Table 8.If thePvalue is greater than α, then the null hypothesis is rejected, which means that the proposed IGWO-SVR method does not have a significant advantage.Data that fit this condition are bolded in Table 8.The less the bolded data, the greater the advantage of the IGWO-SVR algorithm against other algorithms.

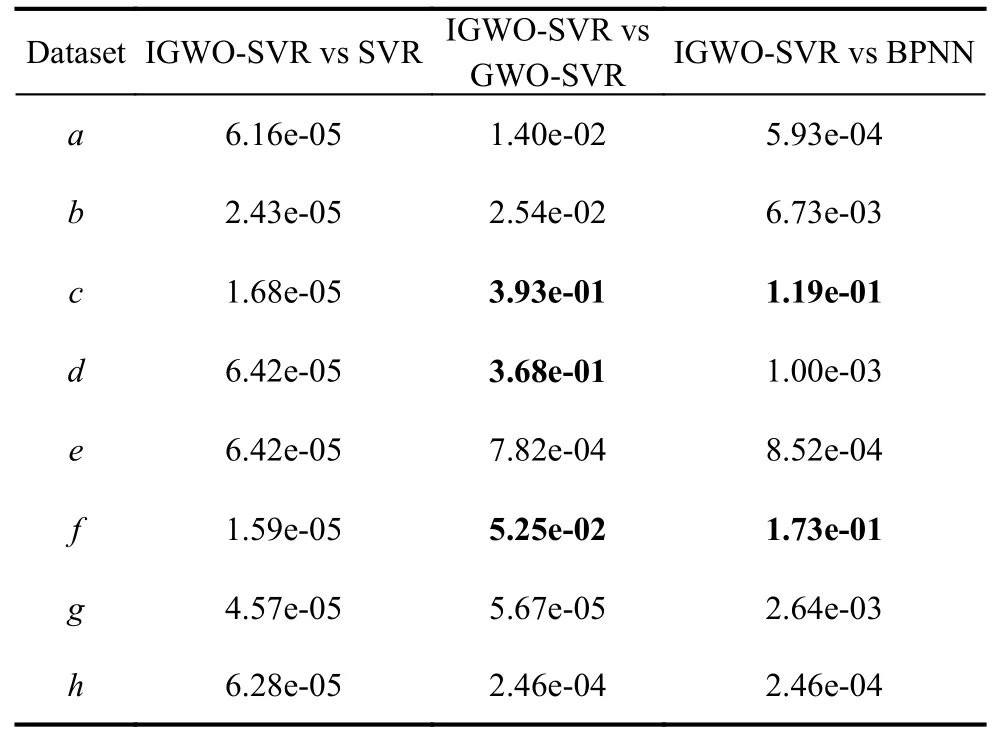
Table 8 P values of IGWO-SVR against other methods using Wilcoxon’s statistical test (bolded if P>α=5%)

In accordance with Table 8, there are eight data sets (a,b,c,d,e,f,g,h) with significant difference when IGWOSVR is compared with SVR.When it comes to GWOSVR, there is no significant difference on datasetsc,d,andf.On the remaining five data sets, IGWO-SVR is with significant difference.In particular, two datasets meet the reject condition of null hypothesis when compared with BPNN.The experimental results above confirm that IGWO-SVR is superior to other methods in terms of prediction accuracy and convergence stability.

5.2 Experiment II

Experiment II aims at verifying the feasibility of the proposed IGWO-SVR method in evaluation of RSS.Data in experiment are derived from simulation under specific operational scenarios, as shown in Fig.9.The orbital parameters of reconnaissance satellite constellation are shown in Table 9 where RAAN means right ascension of ascending node.Based on the scenario, 320 instances are obtained.The number of attributes is seven.TOPSIS method is applied to obtain the effectiveness of RSS according to procedures in Section 4.Input has been normalized to speed up the calculation.The data structure after preprocessing is shown in Table 10, which is divided into training data and testing data.The number of these two parts are 270 and 50, respectively.Following the procedure proposed in Fig.9, the IGWO-SVR model with best SVR parameters is established, thus obtaining the mapping between indicators and the corresponding effectiveness values.

Table 9 Orbital parameters of satellite constellations degree (°)

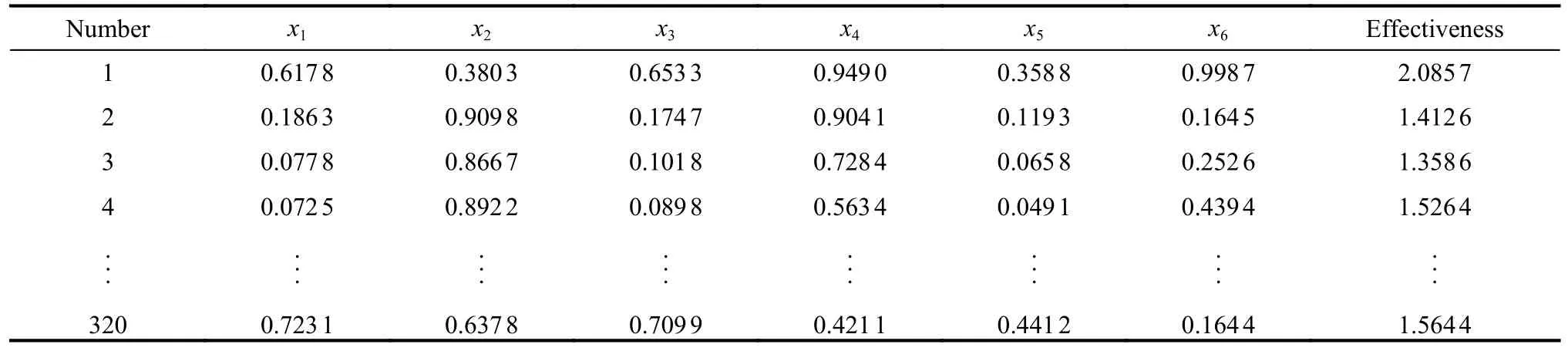
Table 10 Structure of sample data

5.3 Result analysis

For testing the accuracy and convergence ability when dealing with operational effectiveness evaluation (OEE),the prediction result is compared with SVR, GWO-SVR and BPNN model.Initial parameters of these methods are consistent with the first experiment, as shown in Table 5.Through procedures in Fig.9, the optimal parameters for IGWO-SVR are obtained.The penalty factorC=45.16, the parameter of Gauss kernel functionσ= 2.315 8 and the insensitive loss functionε= 0.108.For GWOSVR, the penalty factorC= 5.34, the parameter of Gauss kernel functionσ= 1.092 1 and the insensitive loss functionε= 0.517.The prediction results of the above methods are shown in Fig.11.

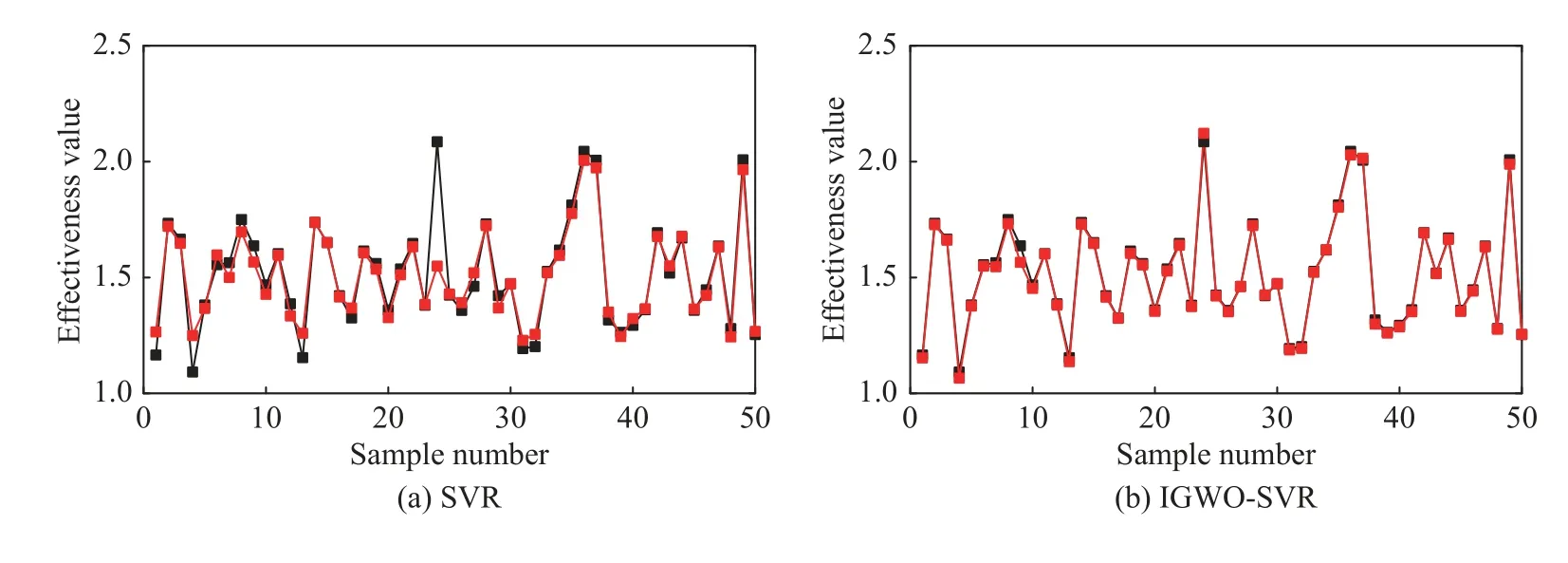
Fig.11 Operational effectiveness evaluation curve

Fig.12 demonstrates the absolute error corresponding to these methods, confirming the accuracy of the proposed IGWO-SVR method.According to Fig.12, the proposed method wins the first place.

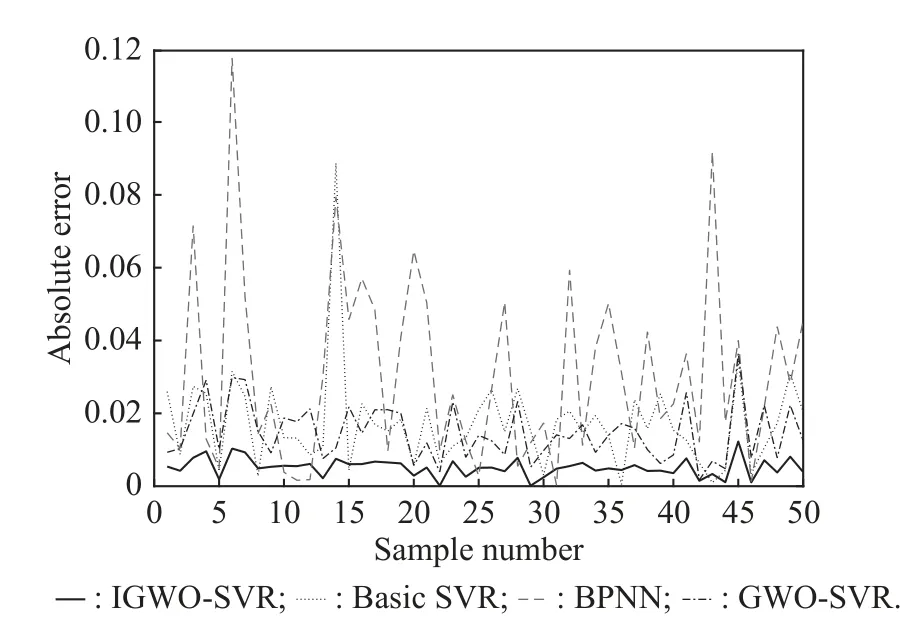
Fig.12 Absolute error curves corresponding to various methods

For offering the comprehensive evaluation on accuracy of these approaches, the root MSE (RMSE), mean absolute error (MAE) and determination coefficient (R2)are calculated.In addition, the computational complexity is calculated to measure the computational cost.In order to reduce the influence of randomness, the process repeats 20 times in the experiment to obtain the average value of these indicators.The definition of each indicator is as follows.

RMSE denotes expected root formula of the square of difference between evaluation results and actual value obtained after inputting each sample data into the model.

whereYi,represent actual and predictive values of theith sample respectively.ndenotes the number of samples.The smaller the value of RMSE, the higher the prediction accuracy of the evaluation model.

MAE demonstrates difference between the predictive and actual values obtained after inputting each sample into the model.MAE has better robustness when data include outliers.MAE does not have the problem of error cancellation, making it more accurate in reflecting the actual error size, as follows:

R2measures how well the model fits the actual value:

whereY¯ denotes the mean of predicted values ofnsamples.

The indicator RMSE, MAE, andR2of SVR, IGWOSVR, BPNN, and GWO-SVR are calculated, respectively, as shown in Table 11.According to Table 11, the accuracy of IGWO-SVR reaches 0.001.TheR2between the predicted value and the actual value reaches 99.7%.Regarding MAE, the values are 0.02, 0.006, 0.04, and 0.02, respectively.IGWO-SVR obtains the best score in RMSE, MAE, andR2.The computational cost of IGWOSVR dealing with evaluation problems is also competitive.When it comes to prediction accuracy and computational cost, IGWO-SVR demonstrates powerful competetiveness.Actually, in order to pursue accuracy in prediction, the integrated method sacrifices a fraction of stability of SVR.Regarding this term, IGWO-SVR realizes a great balance.These verify the proposed method has the optimal comprehensive performance dealing with effectiveness evaluation of RSS.Meanwhile, the proposed IGWO algorithm is worth to be applied in optimizing parameters of SVR.

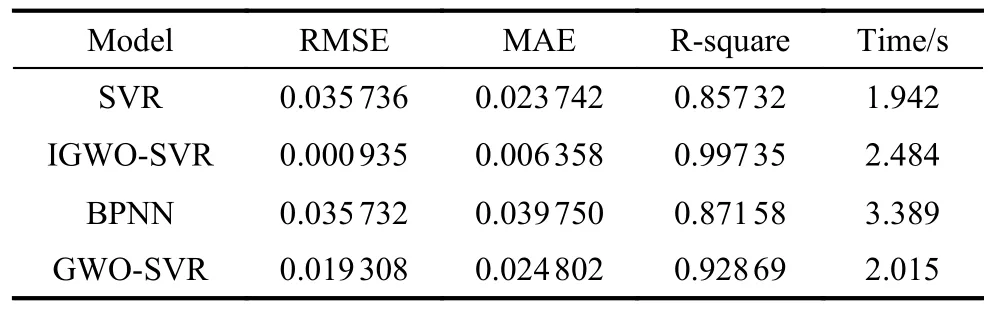
Table 11 Comparison of experimental results

6.Conclusions

Traditional evaluation methods have defects dealing with nonlinear evaluation under small sample conditions, thus these methods are incompetent for effectiveness evaluation of RSS.A comprehensive method optimizing SVR parameters for OEE with the IGWO algorithm is proposed in this paper.Through experiment with 14 benchmark functions, the proposed IGWO algorithm, which is modified by three strategies (opposition-based learning strategy, differential convergence factor and mutation operator) has advantages in improvement of the search rate and swarm diversity.Premature convergence is avoided at the same time.Based on the IGWO algorithm,the proposed IGWO-SVR method is capable of optimizing SVR parameters continuously.Finally, the method achieves optimum evaluation accuracy and corresponding SVR parameters.Experiments are carried out on two aspects: prediction accuracy and computational cost,respectively.The result in Experiment I on eight benchmark datasets confirms the excellent comprehensive performance of IGWO-SVR against rest of methods.Experiment II based on simulation verifies the feasibility of IGWO-SVR in RSS evaluation.

Furthermore, the future work can be carried out from two aspects.The first aspect is modifying the GWO algorithm by developing effective strategies.Another aspect is to extent the method proposed in this work to similar systematic evaluation problems.