Consensus model of social network group decision-making based on trust relationship among experts and expert reliability
WANG Ya, CAI Mei, and JIAN Xinglian
School of Management Science and Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, China
Abstract: Due to people’s increasing dependence on social networks, it is essential to develop a consensus model considering not only their own factors but also the interaction between people.Both external trust relationship among experts and the internal reliability of experts are important factors in decision-making.This paper focuses on improving the scientificity and effectiveness of decision-making and presents a consensus model combining trust relationship among experts and expert reliability in social network group decision-making (SN-GDM).A concept named matching degree is proposed to measure expert reliability.Meanwhile, linguistic information is applied to manage the imprecise and vague information.Matching degree is expressed by a 2-tuple linguistic model, and experts’ preferences are measured by a probabilistic linguistic term set (PLTS).Subsequently,a hybrid weight is explored to weigh experts ’ importance in a group.Then a consensus measure is introduced and a feedback mechanism is developed to produce some personalized recommendations with higher group consensus.Finally, a comparative example is provided to prove the scientificity and effectiveness of the proposed consensus model.
Keywords: social network group decision-making (SN-GDM),trust relationship, expert reliability, consensus model, probabilistic linguistic term set (PLTS).
1.Introduction
In social network group decision-making (SN-GDM), the ultimate goal is to reach a consensus that satisfies every member in a group.However, some experts with or without direct relationships participate in this process, and they come from different knowledge backgrounds.This can easily lead to non-cooperative behavior within the group.In recent years, several studies [1-9] have taken trust relationship among experts into consideration in group decision-making (GDM) issues.Besides, a large number of consensus models have added a recommendation mechanism to increase the consensus level to an acceptable degree.This is profoundly different from the traditional GDM problem.
In recent years, the consensus model based on trust relationship among experts has been widely used in SNGDM.The research work mainly contains the following aspects:
(i) Consensus model based on interaction among experts.This model was mainly developed by Wu et al.[1,2-4].In addition, according to this, several trust propagation operators were proposed, such as the uninorm trust propagation operator [3] and the dual trust propagation operator [1].
(ii) Linguistic information-based consensus model.Experts are inclined to express their preferences with linguistic information, which is assumed more practical in reality [5].Jin et al.[6] explored a probabilistic linguistic preference relations-based consistency and trust relationship-driven consensus model.Wu et al.[7] presented a distributed linguistic trust propagation operator to the SNGDM.
(iii) Consensus model based on psychological factors.In general, experts have different knowledge backgrounds, experiences, or risk attitudes.Hence, they will have a unique psychological perception of the same decision-making problem, which may have an impact on the decision-making result.For example, experts ’ self-confidence or self-esteem would affect the decision-making results [7,8].Liu et al.[8] introduced a consensus model on account of self-confidence, which considers both trust relationship between experts and experts ’ internal selfconfidence.
(iv) Consensus model based on managing non-cooperative behavior.Experts from different groups pay attention to the interests of personal or the organization.To decrease the effects caused by non-cooperative behavior,it is essential to design a novel consensus model to manage it.Du et al.[9] provided a consensus convergence model for managing the non-cooperative behavior in a social network by combining trust relationships with the similarity of opinions.
The above research has enriched the theoretical research of the consensus reaching process (CRP) based on trust relationship among experts.It shows that the real SN-GDM cases are not only related to quantitative mathematical formulas but also some subjective factors of experts [8].Expert reliability is an important concept in GDM.Different scholars have different definitions of expert reliability.Fu et al.[10] defined expert reliability as a combination of the similarities between the preferences provided by experts before the group discussion and the assessments provided by other experts after the group discussion.Xue et al.[11] proposed that the expert reliability is utilized to measure the ability of experts to give a correct evaluation, and it is decided by some factors, such as knowledge, experience, or intelligence of experts.In reality, experts act as boundedly rational, and expert reliability will significantly influence the outcome of the SN-GDM issue.Yet previous studies rarely considered expert reliability, or they simply assumed that every expert has the same reliability [10].
Several studies considered expert reliability in CRP.Most of them employed the similarity of the assessment between experts or the support degree from other experts to reflect expert reliability [10,11].For instance, Fu et al.[10] introduced a novel method based on the evidential reasoning approach to analyze GDM problems by the combination of expert reliability and expert weight.Xue et al.[11] proposed a new CRP by combining expert weight and expert reliability, and at the same time applied the dynamic changes of other experts ’ support degree to measure expert reliability.In addition, Xue et al.[12] also presented a dynamic expert reliability-based CRP to support the distributed preference relations.Nevertheless,almost all studies have ignored the key factor of the matching degree between experts and GDM problems.For example, John is a dentist, and Tom is a repair driver.Mike, who is their mutual friend, asks John and Tom about which surgeon is the best.Assuming that Tom is Mike’s best friend, they have a strong trust relationship,so Mike is likely to follow the advice of Tom.Yet because John is a doctor, it is hard to say whose suggestion Mike will listen to in the end.In this scenario, trust relationship is not the only factor influencing the final decision.The matching degree may be more important than the trust relationship.
In addition, due to the complexity of GDM and the fuzziness of experts ’ assessments, linguistic information is usually applied to represent the preferences of experts.However, in this process, experts would hesitate to choose multiple linguistic terms as their preferences.There is uncertainty in expressing the evaluations of experts with linguistic information.Thus, Rodriguez et al.[13] proposed hesitant fuzzy linguistic term sets(HFLTSs) to solve this issue.Although this method allows experts to give their preferences in multiple linguistic information, the linguistic terms provided by experts have the same weight, which is inconsistent with the actual decision-making environment.The probabilistic linguistic term set (PLTS) allows experts to describe their evaluations by multiple linguistic terms, and it considers the probability of experts selecting different linguistic information [14].The PLTS is the combination of linguistic terms and their corresponding probabilities[14], and it has been used for decision-making problems in different fields, including healthcare management [15],projection evaluation [16], education [17], and emergency management [18].
In SN-GDM, linguistic terms describe experts’ opinions through qualitative information, while probability indicates the possibility of experts holding certain opinions[19-22].This paper selects PLTS as experts’ preferences based on the following two points: firstly, PLTS provides a more natural and accurate way to express opinions for experts; secondly, the properties of PLTS make it superior in aggregating the preferences of different experts through linguistic terms, so that it can be applied to consensus measures.
In this article, we take into account trust relationships among experts and expert reliability simultaneously in SN-GDM.Meanwhile, a matching degree is employed to measure expert reliability.Furthermore, PLTS is introduced to improve the scientificity of expert evaluation in the social network environment.Then a novel consensus model is proposed, including a consensus measure, a feedback mechanism, and a selection process.
Our research framework mainly consists of the following aspects: Section 2 presents some fundamental definitions relevant to PLTS and trust relationship among experts in SN-GDM.Section 3 provides hybrid weights based on trust relationship among experts and expert reliability.Section 4 explores a novel consensus model,including a consensus measure, a feedback mechanism,and a selection process.In Section 5, a comparative case is presented to illustrate the significance of considering expert reliability.This paper is summarized and the future research prospects are put forward in Section 6.
2.Preliminaries
2.1 Basic definitions related to PLTSs
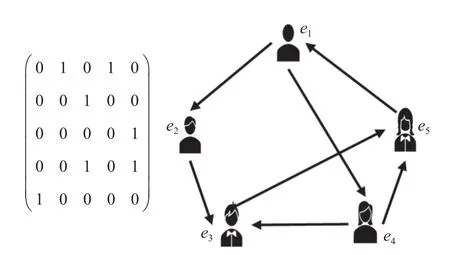
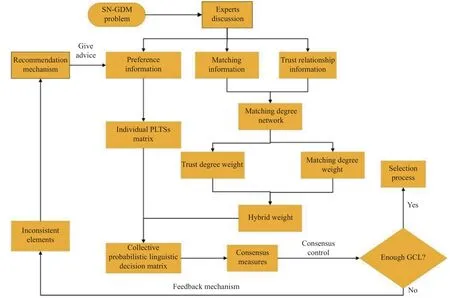
In this paper, a 2-tuple linguistic model is employed to represent the matching level.LetS={si|i=0,1,···,τ} be a linguistic term set (LTS), with the following ranking order, i.e.,s0 Definition 1 [24] Let β ∈[0,τ] be a value obtained by symbolic aggregation in LTS.The function expression of 2-tuple with β as equivalent information is as follows: where α is called a symbolic translation, and round(·) is the general round operation. In addition, the inverse function of ∆ is defined as Based on the discrete LTS, Xu [25] proposed the continuous LTS: It satisfies the following combined operational rule:give two linguistic termsthe following formula can be obtained [26]: In addition, it turns out that due to the complexity of GDM problems, it is incredibly tough for experts with limited knowledge or hesitant to provide crisp numerical preference information.To solve this issue, PLTS is used to describe the evaluation information of experts on alternatives. Definition 2 [14] Assuming thatis an LTS, a PLTS is the combination of an LTS and its corresponding probability.It can be defined as In our research, it is supposed that all PLTSs have been normalized in advance. After defining PLTS, some of its operational laws will be introduced for the following research.Firstly, because the position of linguistic terms can be swapped arbitrarily, the definition of the ordered PLTS is presented: Theorem 1 Give three ordered PLTSsL1(p),L2(p),andL3(p) , λ ≥0. (i) Commutativity: (ii) Associativity: The PLTS possesses combinatorial and multiplication operation laws, but it does not solve how to get the overall consensus level of the group.Hence, a probabilistic linguistic weighted averaging (PLWA) operator is presented to aggregate multiple PLTSs. To determine the consensus level, it is necessary to explore the definition of the distance measure between two PLTS.Distance measure has been widely used for decision-making.In this paper, we employ the Hamming distance to determine the distance between two PLTSs. Suppose that a GDM issue consists ofmalternatives,ncriteria, andlexperts.LetX={x1,x2,···,xm} be the set of alternatives,C={c1,c2,···,cn} is the set of criteria andE={e1,e2,···,el} is the set of experts, wherexirepresents theith alternative,cjis thejth criterion andeudenotes theuth expert.An SN-GDM problem mainly includes three main contents: several experts with or without direct trust relationship, a decision-making problem needed to be tackled, and a common solution required to be obtained.Two processes need to be carried out in SN-GDM problems: consensus process and selection process.In general, the consensus process is dynamic and iterative [27]. In a social network, experts can share their attitudes and communicate with each other.There exist three notational schemes in SN-GDM problems: Graph: Fig.1 shows a social network where nodes represent experts and edges denote trust relationships between experts. Fig.1 Trust network Algebraic: It permits the distinction between several different trust relationships and the different combinations of them.The algebraic form of Fig.1 can be expressed as Sociometric: It is utilized to represent trust relationship among experts.Assumetijdenotes the trust relationship between experteiandej.tij=1 suggests experteitrusts expertejdirectly,tij=0 means that experteidoes not trust expertejdirectly.The corresponding sociometric representation of Fig.1 is as follows: The above three notational schemes denote a binary complete relation.However, experts express their opinions with vague values rather than absolute ‘trust’ or‘distrust ’ in reality.In this paper, a trust network that includes trust and distrust statements is presented to represent trust relationship between experts.Moreover, since there is no direct relationship between some experts in the group, we adopt a dual trust propagation operator to propagate trust or distrust [1]. In the dual trust propagation operator,t-norm is served to propagate trust, andt-conorm is employed to propagate distrust.In addition, thet-norm andt-conorm are represented by the Einstein product ⊗ε, and Einstein sum⊕εrespectively.The definition of the dual trust propagation operatoris asfollows. Definition 5 [1] A tuple of the type λ=(t,d) wheretrepresents a trust degree andddenotes a distrust degree is viewed as a trust function (TF) value, in whicht,d∈[0,1].Let λ1=(t1,d1) , λ2=(t2,d2) ,···, λs=(ts,ds) besTFs, the computation of the dual trust propagation operator is as follows: A mapping on the set of TFs is referred as trust score(TS), where T S ∈[0,1].The TS of experteuis The TS of experts can be used to measure the trust degree weight of experts.According to Yager’s order weighted averaging (OWA) operator, the calculation of the trust degree weight of experts [28,29] is as follows: We would construct a matching degree network, differently from trust network in [1-4].Given a weighted direct graphG={E,L}.LetE={e1,e2,···,el} be a set of nodes, and each node has an associated vector of attribute(feature) values.Each nodeeu∈Erepresents an expert in a group.tijis the edge from experteito expertej.In a matching degree network, edges represent the trust relationship between experts, and nodes represent the reliability of experts.In this article, the trust relationship among experts in a matching degree network denotes the richness of the interaction between experts.We define expert reliability as the matching degree of expert’s knowledge, experience, and talent with GDM issues.It is measured by the matching degree weight of experts.The size of the node is employed to measure the matching degree weight of experts βu(u=1,2,···,l).The larger the node is, the greater the matching degree weight of the expert, and the more reliable the expert is.Fig.2 is the matching degree network of a decision problem.It is shown that experte5has the largest node, which also means that experte5is the most reliable expert in this group. Fig.2 Matching degree network (i) In the short term, it is difficult to change the trust relationship among experts in a group.However, due to the different backgrounds of experts, their reliability in various decision-making issues is inconsistent.This is because experts have a limited range of expertise and it is impossible to be familiar with issues in all fields.For example, there are two GDM questions: which book to read and which computer to choose.The constructed matching degree network can be seen in Fig.2 and Fig.3.Suppose experte3loves reading, so he has high reliability on the first question.However, on the second question, he has low reliability. Fig.3 Matching degree network (ii) Consequently, this paper proposes a matching degree network that combines the same trust relationship between experts and different expert reliability for different decision-making problems, which is helpful to provide personalized recommendations.In order to distinguish the expert weights in traditional GDM problems,this paper defines the expert weights in SN-GDM as hybrid weights.The hybrid weight ϑu(u=1,2,···,l) indicates the importance of experteu, which is the result of considering trust relationship between experts and expert reliability.It not only reflects the overall trust level of experts in a group, but also reflects the reliability level of experts in GDM.The trust relationship among experts is determined by the trust degree weight αu(u=1,2,···,l)obtained in Subsection 2.2.In this paper, the matching degree weight βu(u=1,2,···,l) is employed to represent the reliability level of experteu.Its definition and calculation process will be given in Subsection 3.2. Matching degree indicates the similarity between experts and decision problems.It depends on experts’ knowledge,experience, and talent.The higher the matching degree of experts, the more reliable the evaluation value they provide.The matching degree weight is the normalized representation of the matching degree.In this paper, it is assumed that we can obtain the matching level of experts by conducting background investigations on them.If it is on the Internet, data mining can be used to get relevant information.In order to generate the matching degree weight of experts, it needs to define a matching deviation level (MDL) of experts based on the distance measure. Thus, the matching degree MD(eu) of experteuis Then, the matching degree can be normalized to obtain the matching degree weight βuof experteu: As aforementioned, the hybrid weight of experts can be obtained by aggregating the trust degree weight and the matching degree weight as follows: Let φu(u=1,2,···,l) be the trust degree weight of experteu, and βu(u=1,2,···,l) be the matching degree weight of experteu.The hybrid weight ϑucan be defined as where θ is a control parameter to control φuand βu.The value of θ depends on the type of group.θ=0.5 indicates that trust relationship among experts is as important as expert reliability in CRP.If it is a relationship-oriented group, then the trust degree weight is higher.At this time, in order to reduce the impact of the trust relationship on decision-making, the value of θ should be appropriately reduced. Hybrid weight is a combination of trust degree weight and matching degree weight.The higher the hybrid weight ϑu, the more important the experteuis. This consensus model can be described in Fig.4.Suppose that we can get relevant information of experts,including preference information, matching information,and trust relationship information.Construct a matching degree network through this information.After that, compute the hybrid weights by aggregating matching degree weight and trust degree weight.Then get a collective probabilistic linguistic decision matrix according to the hybrid weights and individual PLTSs matrices.Later, calculate the consensus measure to know if the consensus level has reached the threshold value.If it does, go to the selection process, otherwise use a feedback mechanism. Fig.4 General process of the consensus model In general, we can summarize the implementation of this method into the following steps: Step 4 Feedback mechanism.Judge if consensus control is needed by comparing GCL and the threshold value ξ.If necessary, identify the set of evaluation elements that need to be adjusted, and introduce a recommendation mechanism for adjustment. Step 5 Selection process.The sequence of alternatives is obtained through computing the score of the overall attribute values.We have introduced Step 1 and Step 2 above, and the rest will be covered in Subsections 4.2 and 4.3. A consensus measure is employed to calculate the consensus level of experts and groups.It can judge whether it has reached a satisfactory level of consensus.Hence, it is necessary to introduce a collective probabilistic linguistic decision matrix, which denotes the overall evaluation of different alternatives by all experts under different criteria.In addition, since the fuzziness of expert expression,the combination of probability information and linguistic information can convey the expert’s preferences more accurately.Through the PLWA operator, the calculation formula of the collective probabilistic linguistic decision matrix is as follows: where ϑu(u=1,2,···,l) is the hybrid weight of experteu,andAudenotes the individual PLTSs matrix provided by experteu. Thus, the ICL and GCL can be computed through the collective probabilistic linguistic decision matrix.The consensus measure proves useful for reckoning the differences between experts ’ preferences [19].In former researches, they determined the consensus level through the distance or similarity function obtained by comparing the views of experts with other experts or the group [20].In our research, the distance function is applied to measure consensus, the ICL of experts and GCL are calculated as follows. ICL: LetAube an individual PLTS matrix,A¯ be the collective probabilistic linguistic decision matrix.The ICL of experteuis computed by the opinion distance among individuals and groups: In order to reach a satisfied solution for SN-GDM, a threshold value of consensus ξ ∈[0,1] needs to be predefined.If GCI ≥ξ, then a satisfactory consensus has been reached.Otherwise, it needs a feedback mechanism to enhance the consensus level. The feedback mechanism introduced in this paper mainly contains four steps. Step 1 Judge whether the GCL is higher than the threshold value ξ.This SN-GDM issue is solved if GCL ≥ξ.If not, transform to Step 2. Step 2 Find experts who contribute less to consensus reaching, i.e., those experts whose ICL is below the threshold value: Step 3 For each identified experteu(u∈EXP), compute his/her distance matrix: where Step 4 Identify the maximum element in distance matrix, and get an evaluation element set APS that needs to be adjusted [3]: After obtaining the APS, develop a recommendation mechanism to put forward some personalized recommendations to the corresponding experts: where ζ ∈[0,1], which is viewed as a feedback parameter to control the change rate from the initial preference to the collective preference. If ζ=0, then the collective preference will entirely replace the initial preference, while ζ=1 represents that the initial preference remains unchanged. After that, we can getanovelcollective probabilistic lin guisticdecisionmatrixA¯.Subsequently, recalculate the new ICL and GCL, and return to Step 1.If the threshold value ξ is reached, then take the next step, i.e., the selection process. In the selection process, we can get the overall attribute values of alternatives by the PLWA operator [14].Then the sequence of alternatives can be presented through the arrangement of overall attribute values.The overall attribute values can be calculated as Tom wants to buy a new computer to prepare for the coming college life.Based on the online evaluation, he decides to choose one of the following three brands:HUAWEI, DELL, and HP.Thus, he asks his five friends for advice by considering three criteria: price, appearance, and quality.We can get from this SN-GDM issue that there are three alternative computers {x1,x2,x3}, three criterias {c1,c2,c3} , and five experts {e1,e2,e3,e4,e5}.The weight vector of criteria isw=[0.3,0.2,0.5]T.A 2-tuple linguistic modelS={s0: very low;s1: low;s2: slightly low;s3: medium;s4: slightly high;s5: high;s6: very high} is used to measure matching degree.For example, experte2majors in computer science in college, which indicates that he/she may have a high matching degree on this decision-making issue.At the same time, PLTSs have been utilized to measure the evaluation value of experts with the LTSS={s0: very poor;s1: poor;s2: slightly poor;s3:medium;s4: slightly good;s5: good;s6: very good}.For example, assume experte1is 70% sure HUAWEI under the very good price criterion and he/she is 30% sure HUAWEI under the medium price criterion.Thus, the evaluation value of HUAWEI under the price criterion from experte1is The calculation process is as follows. Step 1 Construct a matching degree network. Assume the matching degree network is shown in Fig.2.Its corresponding trust sociometricTLand the matching matrixLuof experts are as follows: Step 2 Compute the hybrid weight of experts. (i) Compute the trust degree weight of experts. Based on (13) and the shortest trust path propagation rule, we can compute the completed trust sociometricT¯c: Using (21), the collective probabilistic linguistic decision matrix can be aggregated: Then,ICL(A1) =0.868,ICL(A2)=0.872,ICL(A3)=0.858, ICL(A4)=0.924 , I CL(A5)=0.885,GCL=0.882. Step 4 Feedback mechanism.value ξ is 0.890.Due to GCL=0.882<0.890, further In this decision-making issue, we assume the threshold optimization is needed for this decision-making issue. Besides, Thus, EXP={1,2,3,5}.The distance matrix can be computed as follows: To prove the advantage of the algorithms presented in this paper, we will calculate the result of a decision-making issue that only considers the trust relationship between experts, and conduct a comparative analysis.The calculation process is as follows. The collective probabilistic linguistic decision matrix: Due toGCL’’=0.887<0.890, further optimization is needed for this decision-making issue. Thus, EXP={1,2,3}.The distance matrix can be calculated: The results of this example indicate that these two situations have different solutions for a same SN-GDM issue.When considering the combination of trust relationship among experts and expert reliability, the best alternative isx2, otherwise the best choice isx1.It shows that it is not enough to only consider the trust relationship among experts.Expert reliability affects the decision-making results to a great extent. In this paper, we develop a consensus model based on trust relationship among experts and expert reliability to solve different GDM issues.This research has the following contributions: (i) A consensus model is developed by combining trust relationship among experts with expert reliability.And a matching degree network is constructed to solve different GDM problems.Fully considering the internal and external factors of decision-makers is conducive to improving the quality and efficiency of decision-making.Besides, a hybrid weight is calculated by aggregating trust relationship-based trust degree weight and matching degree weight.The hybrid weight shows the importance of experts in a group, and it is a more comprehensive indicator. (ii) We present a collective probabilistic linguistic decision matrix, which is aggregated by the hybrid weight and the individual PLTSs matrix to show the overall evaluation of different alternatives by all experts under different criteria.Since the uncertainty or vagueness of experts in qualitative contexts, the probabilistic linguistic approach has provided significant results.The probabilistic linguistic approach can solve the fuzzy problem of expert preference to a certain extent and improve the scientificity of GDM in the social network environment. Although this paper explores a consensus model based on trust relationship among experts and expert reliability,the two factors considered in this paper are fixed.Nevertheless, in the process of experts’ communication, both of them will evolve along with the decision-making process.In our future research, on the one hand, we will explore how the trust relationship among experts and expert reliability evolve dynamically in different decision-making stages.On the other hand, we will focus on the key factors affecting the change of trust relationship among experts and expert reliability in the decision-making process.Besides, in terms of the expression of experts ’assessments and matching degrees, we will continue to explore more scientific and objective evaluation methods in future research.




2.2 Trust relationship among experts in SN-GDM


3.Determination of hybrid weights
3.1 Construction of a matching degree network
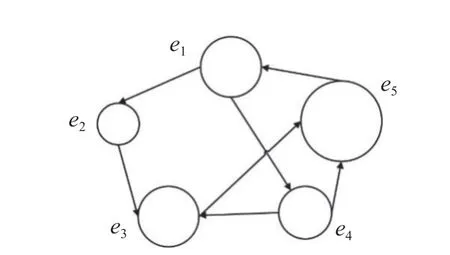
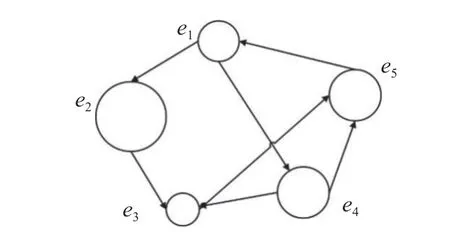
3.2 Matching degree weight of experts

3.3 Hybrid weights of experts
4.Consensus model based on matching degree network
4.1 General process of consensus model

4.2 Consensus measures
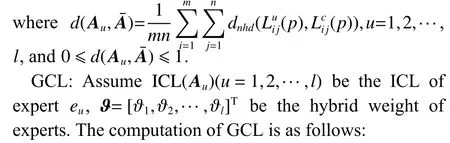
4.3 Feedback mechanism

5.An illustrative example
5.1 Calculation process




5.2 Comparative analysis with trust network



6.Conclusions
 Journal of Systems Engineering and Electronics2023年6期
Journal of Systems Engineering and Electronics2023年6期
- Journal of Systems Engineering and Electronics的其它文章
- Support vector regression-based operational effectiveness evaluation approach to reconnaissance satellite system
- K-DSA for the multiple traveling salesman problem
- Uncertainty entropy-based exploratory evaluation method and its applications on missile effectiveness evaluation
- Formal management-specifying approach for model-based safety assessment
- A cooperative detection game: UAV swarm vs.one fast intruder
- Complex task planning method of space-aeronautics cooperative observation based on multi-layer interaction
