Formal management-specifying approach for model-based safety assessment
XU Changyi, DUAN Yiman, and ZHANG Chao,*
1.School of Control Science and Engineering, Key Laboratory of Intelligent Control and Optimization for Industrial Equipment of Ministry of Education, Dalian University of Technology, Dalian 116024, China; 2.State Key Laboratory of Fluid Power and Mechatronic Systems, School of Mechanical Engineering, Zhejiang University, Hangzhou 310027, China
Abstract: In the field of model-based system assessment,mathematical models are used to interpret the system behaviors.However, the industrial systems in this intelligent era will be more manageable.Various management operations will be dynamically set, and the system will be no longer static as it is initially designed.Thus, the static model generated by the traditional model-based safety assessment (MBSA) approach cannot be used to accurately assess the dependability.There mainly exists three problems.Complex: huge and complex behaviors make the modeling to be trivial manual; Dynamic: though there are thousands of states and transitions, the previous model must be resubmitted to assess whenever new management arrives;Unreusable: as for different systems, the model must be resubmitted by reconsidering both the management and the system itself at the same time though the management is the same.Motivated by solving the above problems, this research studies a formal management specifying approach with the advantages of agility modeling, dynamic modeling, and specification design that can be re-suable.Finally, three typical managements are specified in a series-parallel system as a demonstration to show the potential.
Keywords: model-based safety assessment (MBSA), management, availability, reliability, maintainability, continuous time Markov chain.
1.Introduction
Model-based safety assessment (MBSA) [1,2] is an indispensable branch of system engineering [3].As for a system design document, MBSA merges safety assessment models, such as the continuous time Markov chain(CTMC).They consider the complex behaviors of the system [4,5], and handle the safety requirements verification [6,7], time indicator calculation, etc.[8,9].Normally,the assessment result helps to resubmit an improvement of the dependability of the system’s design.However, the system will not always be static as it is initially designed during its whole life.Various management requirements,such as downtime maintenance, are dynamically set for the system to optimize the system’s service [10,11].These management requirements will always affect the system’s dependability.Although faulty behaviors can be successfully considered in traditional manual approaches, there is still a lack of a formal method to stochastically specify the various managements into the models.
Model generation depends on the skill of the system analyst, and the challenges are as follows.
(i) Complexity specifying: if the system’s scale and behavior complexity increase, the management modeling task becomes trivial and the assessment accuracy decreases [12–14].
(ii) Dynamically specifying: as the management is dynamically set for the system, the models should be resubmitted whenever a new management requirement arrives.It is not possible to employ a group of analysts responsible for this work during the whole lifetime of the system [15,16].
(iii) Multiply specifying: the management specification is not reusable.Although the same requirement is applied, the safety assessment model must be resubmitted for different systems, regardless of the scalability and complexity of the system [17,18].
However, the existing MBSA framework cannot handle formal, automatic, dynamic, and general modeling solutions to overcome the abovementioned challenges.Graphical interface for reliability forecasting (GRIF) [19]has some basic packages for the dependability model generation, such as the Markov chain package and fault tree package.In GRIF, all the management-specified behaviors should be established manually.Management specifications are far from formalized and dynamic.The Boolean-driven Markov process (BDMP) [20] uses the tree models to automatically generate the Markov model.The operator establishes logic gates according to the structure and assigns the leaves according to the components’ behaviors.Particularly, the triggers in its model are applied to denote the happening sequence of the components, which is similar to the destination of expressing management requirements.However, these triggers can only describe the limited failure-related operations, such as cold redundancy management (after the main component breaks down, the expletive component starts to work).It is unable to model repairing-related management.AltaRica [21] is another normally used modeling tool, in which the design document and verification task of the safety critical projects can be programmed.It has rich interfaces with system models such as system modeling language (SysML) [22], Event-B [23], and UPPAAL[24], and these interfaces strongly enhance its modeling ability.However, aiming at the management expression,AltaRica only handles it by manually detailed coding programs.This loses formalization and increases the complexity of model generation.
This study aims to achieve a formal management-specifying approach to assess the systems in the form of the CTMC model.The specifying approach is achieved by converting the CTMC into an event-driven automaton(EDA) and designing the specification automaton based on multiple management requirements.With the help of a safety assessment model synchronized with the specification automaton, the system assessment model will be generated.
The main advantage of this study is: there is no need to modify the previous CTMC assessment model due to that any new management requirement can be specified by further synchronizing its coherent specification automaton.In addition, the same management requirement specifying the task is solved by following the same establishing principle for different systems.
In this study, a formal management specifying approach with the advantages of agility modeling,dynamic modeling, and specification design is proposed to be used in a series-parallel system.Firstly, the background, big issues, and basic models are reported.Secondly, the formal specifying approach to solve the problem is used.Finally, a benchmark to further interpret the solution is applied.Through this paper, three widely applied system management requirements, “system downtime maintenance (DM)”, “component first failed first repaired (FFFR)” and “special component has the priority to be repaired (PtR)”, are specified in the availability,reliability and maintainability CTMC models in a seriesparallel system.
1.1 CTMC model
As a stochastic process, the Markov process is named by the Russian mathematician Andrey Markov.System performances are described as variable states, and the transitions are used to illustrate the relationships among the states.The Markov process has the memoryless property:if the value in the current state is already known, the variable value in the next state only depends on this current state without recalling the system’s history [25].The discrete-time Markov chain and CTMC are two model branches of the Markov process.The discrete time Markov chain model is regarded as a system driven by a common time clock, and the transitions among the states are distributed by probability.In contrast, the CTMC considers the occurrence rate of various events, while these events contribute to state transit [26].A CTMC describes a faulty/repairable system from the viewpoint of safety analysis.There are two states, an initial system working state and a system broken down state, and the transitions are driven by real time, denoted by failure rate and repair rate.If the CTMC is achievable, the equivalent transition matrix and state equation are achievable, which makes mathematical calculations possible [27,28].As the CTMC is naturally suitable for describing the systems,and its calculating function can be used for the assessment task, the CTMC is a widely applied modeling approach in model-based safety analysis.With the help of the Laplace solution, the CTMC assesses the system by calculating time indicators: for availability CTMCA(t), it calculates the mean time before failure (MTBF); for reliability CTMCR(t), it calculates the mean time to failure(MTTF); for maintainability CTMCM(t), it calculates the mean time to repair (MTTR) [29–31].The assumption of the CTMC to transition matrix is: (i) the rate is the happening rate of the transition; (ii) the sum of the happening ratexishould be “1”,, which means all the possibility is considered.
1.2 Availability CTMC model
Both the failure and repair system characteristics are considered in availability model.The definition of the availability function is denoted byA(t); in a certain situation,the rate of the system contributes its function at a certain timet.The availability CTMC model presents all the possible functional and dysfunctional situations by state,while the model transition presents the possible failure rates and repair rates [32].
State 1 is the initial state, which means the system is initially working healthily.And, by failure rate “λ”, the system breaks down to state 2.From state 2 to state 1, the system can recover by a successfully repaired rate “μ”.
1.3 Reliability CTMC model
The performance during healthy working to breaking down is depicted in the reliability model.Reliability is defined to be in a certain situation, and in a certain period(0,T), the system achieves its desired function.At timet=0, the system is working completely healthily, and at timet=T, total breakdown occurs in the system.In the meantime, in (0,T), the rate of the system ability to achieve its function is denoted byR(t) and 0≤R(t)≤1[32].
The model starts from state 1 (healthy state); by a failure rate ofλ, the system breaks down to state 2, and then,this model ends.
1.4 Maintainability CTMC model
The characteristics from breaking down to finally healthy operation are depicted in the maintainability model.The definition of the maintainability function, denoted byM(t), is the system successfully recovering its rate in a certain situation in a demanded time period (0,T).After the failure occurring in this repairable system, as a quantification description of system reparability by rate,M(t)is: at the beginning timet=0, the system is in the failure situation, and beforet=T, the system recovers to a healthy function.
The initial state of the maintainability model is state 2(describing the system starting from the brokendown state); by a successfully repaired rate “μ”, the system reaches healthy state 1, and then, the model ends [32,33].
2.Management-specifying approach
This part studies the management-specifying approach.Subsection 2.1 generally introduces the workflow of this approach, and it mainly has two important steps: the first step is to convert CTMC to EDA, which will be presented in Subsection 2.2; the second step is to design the specification automaton to specify the MBSE models,which will be presented in Subsection 2.3.
2.1 Management-specifying proposal
The work of Ionescu enables the CTMC model to be transformed with EDA by regarding the occurrence rate of the transition events directly presented by the events[34].Therefore, when only focusing on the events and the local component transition events are unique (although the component transition event rate values are probably the same, it is supposed that the events are also unique),the occurrence rate of the events in the CTMC can be equivalent to the transition events in EDA [35].
Based on the specifying solution in discrete event system theory [36,37], management can be modeled as specification automata.After the synchronization of EDA and specification automata, EDA is able to contain specifying information.
As it is depicted in Fig.1, this specifying solution is

Fig.1 Management requirements specifying the algorithm
(i) Based on the system structure and the component behaviors, the availability, reliability, and maintainability CTMC models are established as normal.
(ii) These CTMC models are translated into EDA.
(iii) According to the management, the specification automata are designed.The synchronize operation of EDA with specification automata produces the specified safety EDA models.
(iv) The specified EDAs are translated back into CTMCs for the purpose of assessment.
2.2 Equivalence model conversion: CTMC and EDA
Explained in (1) and (2), the system behavior is described as a discrete languageLsys.Lsyscan be regarded as the union of sublanguages associated with every state, and sublanguageLiassociated with state xi is defined as the universe of event sequences, while the events drive the system from the initial state to the considered state xi:
Based on Arden’s rule [38,39], the CTMC can be presented by a sequence of events instead of the event occurrence rates.In (2),AandBare the universe set of event sequences, and the sublanguageLiis as follows:

The CTMC is defined by the following:
whereQmcis the state set,Emcis the transition set, δmcis the transition function explaining the state evolution relationship excited by the transitions, andq0mcis the initial state.Based on CTMC definition and the system can be presented by the union of sequences of event-associated states, the states xi union in (1) is equivalent to the state set in the CTMC:
The transition function in the CTMC describes the transition relationship between states and focuses on the events causing the state transition.The transition function δmcin the CTMC is equivalent to the system describing languageLsys:
The EDA is defined as follows:
whereQEDAis the state set,EEDAis the transition set,δEDAis the transition function,q0EDAis the initial state, andqmEDAis the marked state.By the same principle, according to (1) and (2), we can also obtain the state set:
Additionally, the transition function is described by the system describing language:
Assumeexyis one of the system events, and it causes the state to evolve from one statexto another stateyby the rate ofR-exy.Because the CMTC and EDA describe the same system, the conclusion is as follows:
which can be further explained as follows:
It is equal to the following:
For example, in Fig.2, the models describe repair with an initial working state S0 and a failure meaning state S1.The failure event (denoted by f1) occurs at the rateλ, and the system successfully repairing operation (denoted by r1) occurs at the rateμ.According to (1) and (2):
whereL1= (L1r1)f1, and the solution is as follows:
Therefore, for the conversion of the CTMC and EDA,the events drive the state transition, and each event has an occurrence rate shown in the middle of Fig.2; thus, the state set is as follows:
In CTMC,
In EDA, which is equal to the following:
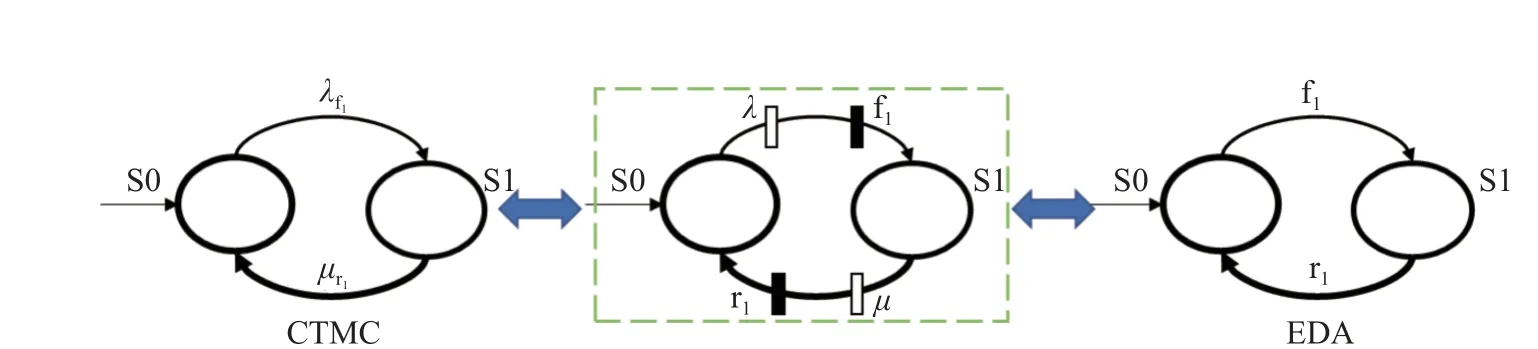
Fig.2 Model conversion between CTMC and EDA
2.3 Management-specifying method by using an EDA synchronize operation
In the field of discrete event system theory application,the specification automaton is designed to contain the specifying information.With the synchronize solution of the EDA and specification automaton, management-specifying demand is achieved.The specification automaton is defined as follows:
whereQSPis the state set,ESPis the transition set, δSPis the transition function,q0SPis the initial state, andqmSPis the marked state.
Then, the result of the synchronize operation (denoted“//”) [37] is also an automaton, and this specified automaton (denoted “SPA”) is defined as follows:
where Ac is the accessible part, and the symbol “ ×”denotes the Cartesian product [40,41] between the state set or transition event set.
The transition function of SPA is inspired by the transition function of SP and EDA, and it is explained by the following equation.Here, the symbol “” denotes the complement set operation in (16).
Assume the following management requirement: among all the components in the system, the most important one owns the priority to be repaired firstly.Fig.3 shows a series-structural system constructed by G1 and G2.When both of these components are broken down, G1 has the priority to be repaired first.
In Fig.3, series system is the availability model of this system:
these states respectively mean: both G1 and G2 are working; G1 is working, but G2 is broken down; G1 is broken down, but G2 is working; and both G1 and G2 are broken down.
The transition function δEDA1that evolves the states is shown in Fig.3.According to the management requirement, when both components are broken down (state B1.B2), the first repair operation should be distributed to G1, which means that transition B1.B2→-r1W1.B2 is legal and transition B1.B2→-r2W1.B2 is illegal.Therefore, to express a management requirement, the illegal transition should be dismissed by a formal solution.
In Fig.3, the specification automaton SP1 is
whereQSP1={S0,S1};ESP1={f1,f2,r1,r2};q0SP1={S0};andqmSP1=∅.The transition function is as follows: the self-loop events of S0 are {f2,r1,r2}, driving no state evolution from S0 to S1, since these events do not break the management requirement.Then, the transition from state S0 to S1 is event {f1}; the statement “if f1happens, the requirement should begin to be respected” is considered;the self-loop of S1 is {f1,f2}, where there is no repair operation r1or r2, since after f1happens there should be no repair operation distributed onto G2 and r1will be further treated; from S1 to S0 is repair operation r1, since after f1happens G1 should be repaired and turns to the initial state.
The synchronize result of SP1 and EDA1 is


then
where
where this state does not exist.As the synchronization result has been dismissed, the G2 repair operation event r2from both components is a broken down state (B1.B2.S1), and the management requirement is satisfied.
In summary, whenever a management requirement arrives, the CTMC can be translated into EDA.The SP(specification automaton) is designed.By the synchronization operation of EDA and SP, the SPA can be achieved.Translating SPA to the CTMC model, a manageable CTMC that satisfies the management requirement is generated.
3.Management requirements specifying the benchmark
Various management requirements are set in a practical application process, and the variety of system architectures and system behaviors further adds to the complexity of generating the model.This solution has the advantage of agility.Facing various CTMC models, one kind of management requirement has one consistent specifying solution.For example, in Fig.3, the system architecture is a series of working systems constructed by two components, and in Fig.4, the system architecture is a seriesparallel working system constructed by three components.Obviously, these two different systems have different availability models.However, if the management requirement demand is the same as “One of the components has the priority to be first repaired”, the specification automaton must be uniform, as depicted in Fig.3(c)and Fig.5(c).Moreover, this uniform specification automaton design is suitable for all CTMC models.

Fig.4 EDA models

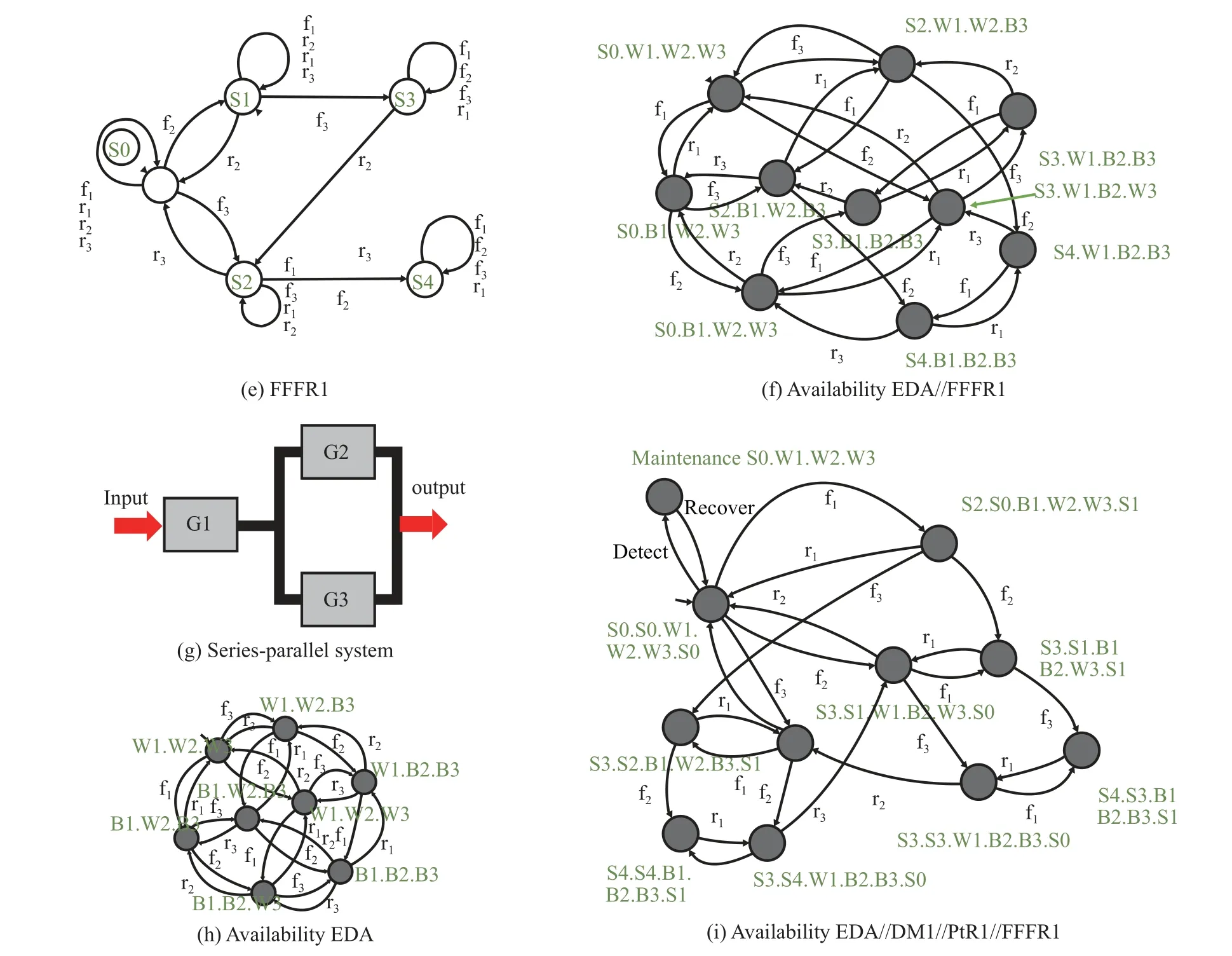
Fig.5 Availability model specified by various management requirements
As the management requirements are uncountable in reality, this part offers a benchmark for three widely used management requirements: DM, PtR, and FFFR.A seriesparallel system is used to study this specifying solution.Component G1 has PtR for its relatively important position.Components G2 and G3 are repaired according to FFFR, assuming that G2 and G3 are lying in similar positions.The whole system needs a DM at the initial state,and all the components are healthy (“test” behavior for beginning of maintenance and “recover” behavior for system recovery to work).These management requirements are specified for availability, reliability and maintainability models.Based on the algorithm shown in Fig.1, as the converted CTMC and EDA are already introduced,this example begins from the system EDA models.After the specified EDA models are achieved, the specified CTMC will be reasonably achievable.
3.1 Repairable series-parallel system
To illustrate the specifying method of different management requirements, a typical series-parallel system is studied.Depicted in Fig.4(a), this system is constructed by three components, G1, G2, and G3, and they are all repairable if broken down.G1 treats the system input, and its output feeds the input of G2 and G3.G2 and G3 both contribute their output to the system’s production.
Moreover, as shown in Table 2, each of these components has unique behaviors, which means that the transitions in the CTMC model and EDA model are unique (λiis the failure rate, fiis the failure event,μiis the successfully repaired rate, and riis the successfully repaired event).
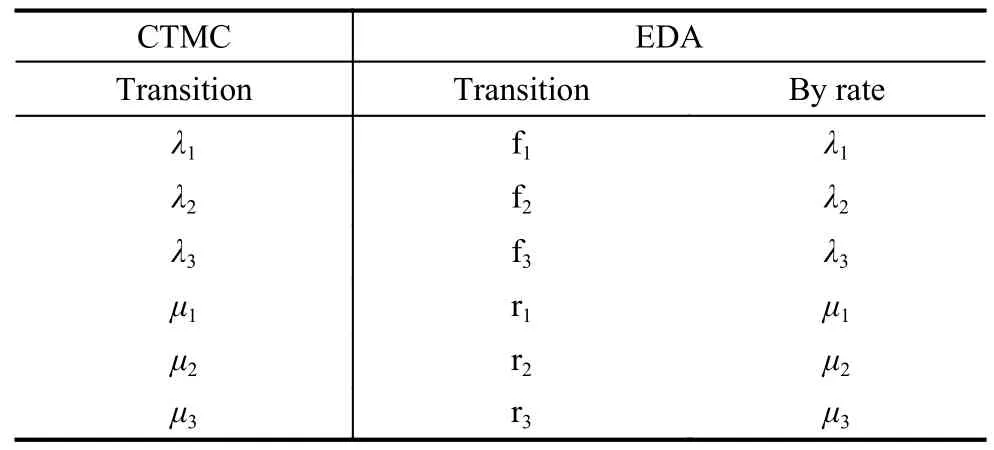
Table 2 Transition equivalence conversion
According to the definitions of availability, reliability and maintainability, the corresponding models are established in Fig.4.Availability denotes the system initially working healthily.With the possible failures of each component, the system is totally broken down, and each component can be repaired.Reliability only focuses on how the system breaks down, and maintainability only focuses on how the system recovers, while during breakdown and recovery, the components can be further broken and repaired in a timely manner.For the state names,“Wi” is the “working” situation of Gi, and “Bi” is the“broken down” situation of Gi.For example, in the reliability model, the models start from W1.W2.W3, which means that these three components are all working healthily.Whenever G1 breaks down by f1, the system comes to B1.W2.W3, which means G1 is broken down and G2/G3 are working healthily, and then the model ends because the system is totally broken down.
3.2 Availability model-specifying approach
The downtime maintenance management requirementspecifying solution is illustrated by a new state in which the maintenance operation is added to the original availability model.From the initial state in which all the components are working well, driven by the system test operation, the system reaches the maintenance state.After maintenance, driven by the “recover” operation, the system recovers to work.In Fig.5(a), the automaton is designed by the semantic “keep the availability model as original and adding a maintenance state into the model”:first, the maintenance state changes from the initial state,and then, the transition between states S0, S2, S3, and S4 are {f1, f2, f3} and {r1, r2, r3}, describing the availability model.“From the initial state, a stochastic state is reached, and the failure of G1, G2, and G3 occurs, as well as the repair operations”.Based on (3), the synchronized result of the specification automaton and original automaton is in Fig.5(b).This result satisfies the management requirement by adding a state (maintenance.W1.W2.W2)that represents the system maintenance operation driven by “test” and “recover” events.
Already introduced in the example of the series system in Fig.3, because G1 is the priority and the first to be repaired, the specification automaton PtR1 in Fig.5 is designed: in case the failure of G1 happens (in PtR1, the transition isno repair operations of G2 or G3 should happen while the only allowed repair r1 if returning to the initial state.The specified model is Availability EDA//PtR1, which satisfies the management requirements; for example, state B1.B2.B3.S1 indicates that all components are broken down, and the output transitions of this state have only one repair r1: “until component G1 is repaired, G2 and G3 are allowed to be repaired”.

For some cases, after the system has been specified by one requirement and another requirement comes as a supplement, there is no need to design a specification automaton to contain all the information of these two management requirements.With the precondition that“The multiple management requirements aiming at one system are not conflicting”, this research offers a stochastic multi-specifying function by continuously varying specification automata, where each specification automaton contains one kind of management requirement, without the necessity of modifying the previous models regarding compatibility.For example, as shown in Fig.5,as series-parallel system management requirements are as follows: (i) G1 has the priority to be first repaired, as presented by PtR1; (ii) G2 and G3 share the “first broken down, first repaired” condition, as presented by FFFR1;(iii) the system needs downtime maintenance, as presented by DM1.These multiple management requirements are comprehensively specified into the system model by synchronizing the refereed specification models EDA//DM1//PtR1//FFFR1.


PtR1//FFFR1 and also suitable for Subsection 3.3 and Subsection 3.4.
3.3 Reliability model-specifying approach
The reliability EDA of the series-parallel system shown in Fig.6 presents the system from the initially healthy working to the system broken down, and this reliability EDA naturally satisfies the management requirement “G1 should be repaired first” because if G1 is broken down, the model stops without applying a further repair operation to G1 (state B1.W1.W2, state B1.W2.B3 and state B1.B2.W3 are absorbing states); additionally, this reliability EDA also satisfies “G2 and G3 are first broken down and first repaired” because when G2 and G3 are both broken down, the reliability model stops without a further repair operation (state W1.B2.B3 is an absorbing state).Therefore, the only management requirement that should be specified is downtime maintenance.
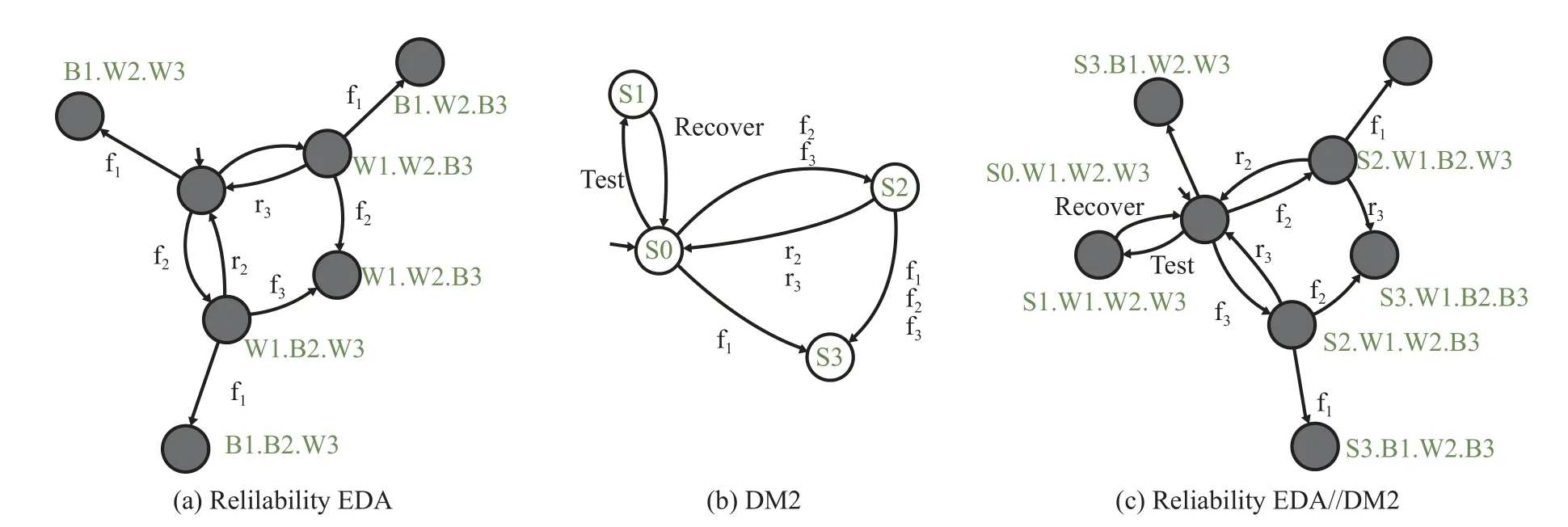
Fig.6 Reliability model specified by downtime maintenance management requirement
The downtime maintenance management requirement specifying automaton DM2 is shown in Fig.6, since the same establishment principle is already introduced in DM1, which is: adding a maintenance state to present downtime operation from the initial state.Moreover, the transitions among S0, S2, and S3 are applied to describe the behaviors of the reliability EDA, ensuring that the synchronized result will remain the same transition situation as the reliability EDA.Based on (3), the synchronized result is reliability EDA//DM2, which satisfies this management requirement.
3.4 Maintainability model specifying approach
Unlike the reliability and availability models, the initial state of the maintainability model is B1.B2.B3, because the maintainability model assesses the system characteristics recovering from the total broken down state to working state.Aiming at this series-parallel system, the management requirements “G2 and G3 first fail and are first repaired” or “system downtime maintenance” are not suitable; the only specifying task is for “G1 has the priority to be first repaired”.
In Fig.7, transitions between states S0 and S1 allow component G1, “repair” and “failure”, and transitions from states S1 to S2 further repair G2 and G3.This specification automaton design can ensure that the model can freely repair G1, and after G2 or G3 is further repaired,the series-parallel system recovers to a healthy state.Then, the maintainability model stops, without the possibility of failure occurring in G2 or G3 (depicted in PtR2,where state S2 is an absorbing state); thus, the management requirement is satisfied.

Fig.7 Maintainability model specified by priority to be first repaired management requirement
According to (3), the specified result is shown in maintainability EDA//PtR2, where the management requirement is satisfied.
This approach can be developed to be a safety-assessment tool package as a software plug-in of the engineering tools.This application could serve the full life cycle of the industrial systems.
In the system designing stage, the hardware structure is integrated to be the EDA, and the planed managements are integrated to be the specification automata (SP).By synchronizing EDA and SP (SPA=EDA//SP), the specified models (SPA) which fuse the managements and the system structure are made.After several times of iterations and upgrades, a safety critically considered system is able to be produced.
In the operation and maintenance stage, various situations can timely happen to the industrial system, for example, A: objective change, B: new management plans,C: maintenance requirements, etc.Whenever these new managements arrive, the system operators work on the tool and assign the corresponding SPs (SP-A, SP-B and SP-C) and the dynamic specified model SPA=EDA//SPA//SP-B//SP-C is obtained.Dynamic reliability, availability and maintainability models are handled, as well as model-based assessment can be realized in actual system.
4.Conclusions
This research provides a stochastic management requirement specifying approach for system assessment CTMC models by converting the CTMC model into EDA models and designing specification automata based on various management requirements.After the synchronize,operation is applied to the specification automata and the system EDA models, a management requirement specified system EDA model is obtained.With the further conversion from EDA to the CTMC, the management requirement specified CTMC is achievable, and the system can be assessed considering the management requirements.In this paper, a benchmark of a series-parallel system constructed by three faulty and repairable components is applied, while three popular applied DM, PtR, and FFFR management are specified in the availability, reliability,and maintainability model of this series-parallel system.
Due to the agility of this approach, with the precondition of “the multiple management requirements aiming at one system are not contradictory”, one principle specification automaton is established according to one kind of management requirement.Moreover, in case multiple management requirements are set, the specifying solution is illustrated by multiplying and synchronizing the corresponding specification automata.
By the normal approach of merging the safety assessment model based on the system architecture and system behaviors, if one new management requirement is set in the system, the safety model should be resubmitted to satisfy this management requirement, which requires redundant work by a system analyst.Additionally, even given the same management requirement, facing a different system, a new safety model should be also resubmitted,regardless of the scalability and complexity of the system.These two problems are solved in this research by management requirement coherent specification automata synchronized with the previous safety assessment model and by following the same specification automaton establishment principle.
Countless management requirements exist according to different stochastic situations and different systems, so this research provides an open issue for specifying approaches.
 Journal of Systems Engineering and Electronics2023年6期
Journal of Systems Engineering and Electronics2023年6期
- Journal of Systems Engineering and Electronics的其它文章
- Support vector regression-based operational effectiveness evaluation approach to reconnaissance satellite system
- K-DSA for the multiple traveling salesman problem
- Uncertainty entropy-based exploratory evaluation method and its applications on missile effectiveness evaluation
- Consensus model of social network group decision-making based on trust relationship among experts and expert reliability
- A cooperative detection game: UAV swarm vs.one fast intruder
- Complex task planning method of space-aeronautics cooperative observation based on multi-layer interaction
