Algorithms for automatic measurement of SIS-type hysteretic underdamped Josephson junction’s parameters by current-voltage characteristics

Aleksey G.Vostretsov,Svetln G.Filtov

a Laboratory of Quantum Cryogenic Electronics,Novosibirsk State Technical University,Novosibirsk,630073,Russia

b Chinakal Institute of Mining,Siberian Branch,Russian Academy of Sciences,Novosibirsk,630091,Russia

Keywords:Algorithm design and analysis Critical current Current-voltage characteristics (IVCs)Josephson junction (JJ)Measurement errors Parameter estimation

ABSTRACT Some electrical parameters of the SIS-type hysteretic underdamped Josephson junction (JJ) can be measured by its current-voltage characteristics (IVCs).Currents and voltages at JJ are commensurate with the intrinsic noise level of measuring instruments.This leads to the need for multiple measurements with subsequent statistical processing.In this paper,the digital algorithms are proposed for the automatic measurement of the JJ parameters by IVC.These algorithms make it possible to implement multiple measurements and check these JJ parameters in an automatic mode with the required accuracy.The complete sufficient statistics are used to minimize the root-mean-square error of parameter measurement.A sequence of current pulses with slow rising and falling edges is used to drive JJ,and synchronous current and voltage readings at JJ are used to realize measurement algorithms.The algorithm performance is estimated through computer simulations.The significant advantage of the proposed algorithms is the independence from current source noise and intrinsic noise of current and voltage meters,as well as the simple implementation in automatic digital measuring systems.The proposed algorithms can be used to control JJ parameters during mass production of superconducting integrated circuits,which will improve the production efficiency and product quality.

1 Introduction

Superconducting cryogenic electronics is one of the rapidly developing areas in electronics at present.Its formation is due to the achievements of scientists in the field of superconductor physics and the significant progress in the field of nanotechnology.The key element of cryogenic electronics is a Josephson junction (JJ).Researchers all over the world are working on the creation of new technologies for producing both high-temperature superconductors (HTSs) and low-temperature superconductors (LTSs) [1–4].Among different types of JJs,the superconductor-insulator-superconductor (SIS)-type junctions have the widest applications.A lot of new devices based on JJs have appeared.These are superconducting quantum interference devices (SQUIDs) [5],single photon counters [6,7],superconducting qubits [8,9],cryogenic memory [10,11],radio astronomy devices [12],high-temperature superconductors [13],etc.

Superconducting integrated circuits (SICs) have been developed,and some enterprises manufacturing such SICs emerged [14].SIC manufacturing includes producing thousands of JJs.Under these conditions,JJ should have parameters that are repeatable with high accuracy.Therefore,a necessary step in creating and studying a novel element based on JJ,developing and debugging the manufacturing technology,and monitoring its mass production is the measurement of its parameters.

The rapid development of digital and information technologies since the 80s of the last century has led to a new approach to the creation of testing and measuring instruments [15,16].Measurement and instrumentation science has begun to be treated as “a coherent part of the science of information,systems,and computing,with distinctive features” [17].Digital information measuring systems have become widespread.The usage of the digital measuring technology has allowed automating the testing and measuring processes.In addition,it improves the accuracy and reliability of measurement results,including that in the noise environment [18,19].Automation of the testing and measuring processes is especially important for the mass production.

A characteristic feature of measuring the JJ parameters is that the measurement results are significantly affected by inherent thermal and quantum noise both in the measuring instruments including the voltage and current meters and in JJ itself [20–25].This leads to the need for multiple measurements with subsequent statistical processing of their results.A relevant problem is the development of algorithms that would allow multiple measurements and automatic verification of the JJ parameters in a digital form with the required accuracy.

The automatic measurement of parameters requires an adequate mathematical model for the sample to be measured.The resistively and capacitively shunted (RCSJ) models proposed by McCumber [26],Stewart [27],and Johnson [28] are the first and frequently used models of JJ.For this kind of models,a balance equation of currents is used to obtain the current-voltage characteristic (IVC).Using the RCSJ model,Alam et al.[29]proposed a Verilog-A based compact model to simulate both hysteretic and non-hysteretic current-voltage responses for SIS-type JJs.Based on a tunnel junction microscopic model,a different model has also been proposed,which makes it possible to derive an analytical expression of IVC of generic junctions [30,31].

This paper focuses on the automatic measurement of five basic electric parameters of SIS-type hysteretic underdamped JJs by IVC,including the critical currentIc,the gap voltageVg,the maximal currentIgat the gap voltageVg,the normal resistance of the junctionRN,and the resistanceRlgwhich characterizes the leakage current of the barrier layer due to the imperfection of the interlayer material.These parameters are very important for the design of quantum cryogenic electronics.The quality of SIS-type JJs is evaluated by the ratio of the resistancesγR=Rlg/RN.The critical currentIcand the maximal currentIgare important for the design of microwave single photon counters [6,7].To improve the detection efficiency of the single photon counters,the critical currentIcshould be as close as possible to the maximal currentIg.To estimate JJ overheating when it switches into the resistive state,the normal resistance of the junctionRNshould be measured.Here the case is considered where JJ overheating is negligible.The proposed approach to the synthesis of the measurement algorithms can be applied to further develop parameter measurement algorithms for different types of JJs,which have appropriate mathematical models.

Most of the studies devoted to measuring IVC of JJs focus on the critical current measurement technique.The classical method is based on the dependence measurement of the voltage across the junction on the current flowing through it [32–34].Then the desired parameters are determined according to the obtained dependence.In order to reduce the influence of noise,multiple measurements are carried out to average the values of the measured voltages and currents.Reference [32] describes the direct measurement technique of the Josephson supercurrent in ultra-small JJ by using the SQUID series array with 100 direct current (DC)SQUIDs.Reference [34] proposes to employ the first and third harmonic lock-in measurements of the junction resistance in the critical current measurement procedure.

However,there is no published literature on developing algorithms exactly for the automatic measurement of all parameters by IVCs of JJs.Han et al.firstly adopted digital measuring systems to obtain the preconditions for the automatic measurement of DC parameters of SIS-type hysteretic underdamped JJs [35].They proposed to drive JJ by a sequence of triangular current pulses,and to take the current and voltage readings at the junction by a data acquisition board synchronously.They defined the critical current value for each pulse as the value of the current reading at which the voltage on the junction exceeds a certain threshold.Statistical processing of the measurement data was performed on a computer.However,only two parameters (the critical current and the normal resistance) were evaluated in this work.In addition,Han et al.did not take into account the discrete nature of current and voltage data acquisition,which leads to an additional measurement error.The noise influence of the current pulse generator and measuring instruments on the resulted error was also not considered.

Similar to the most well-known studies [36–38],typical IVC of SIS-type hysteretic underdamped JJ(Fig.1) is used for the algorithm synthesis in this paper.

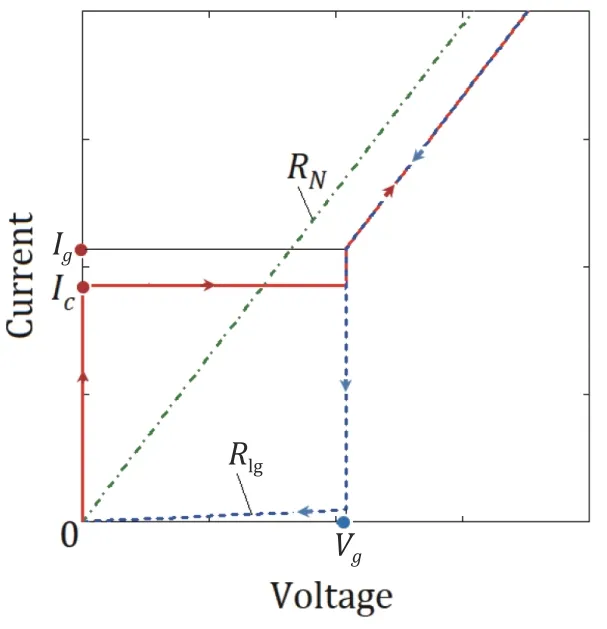
Fig.1.Typical IVC of SIS-type hysteretic underdamped JJ.

Since the gap voltageVgfor the SIS-type hysteretic underdamped JJs is relatively high (for Nb/AlOx/Nb junctions,Vg≈3 mV at the temperature of 4.2 K),it is easy to measure the voltages in the range ofV≥Vg,but the current remains relatively low.Therefore,the main difficulty is to realize the automatic measurement in the irregular IVC range.For the SIS-type hysteretic underdamped JJ,this means the automatic measurement of the currentsIcandIg,as well as the resistanceRlg.

In our previous work [39],an algorithm is proposed to automatically measure the critical current of the SIS-type hysteretic underdamped JJ based on the data obtained similarly to Ref.[35].To further develop the algorithms for the automatic measurement of parameters of SIS-type hysteretic underdamped JJs,here the algorithms are proposed to measure five parameters of the SIS-type hysteretic underdamped JJ for automatic digital measuring systems.Finally,the algorithm performance is studied through computer simulations.

This paper is organized as follows.Section 2 presents the measurement system and the model of observed processes.In Section 3,an algorithm is proposed to check the operability of JJ.In Section 4,the extended description of the critical current measurement algorithm proposed in Ref.[39] is presented.In Section 5 and Section 6,algorithms are proposed to measureRlg,as well asRN,Ig,andVg,respectively.Finally,the simulation results and conclusion are given in Section 7 and Section 8,respectively.

2 Model of the observed process

Fig.2 schematically illustrates the automatic system used to measure the JJ parameters.A current pulse generator generates a packet of triangular current pulses.A current meter and a voltage meter with a set sampling period synchronously form the vectors of current and voltage readings at JJ,which are then transmitted to a digital processing device.Finally the parameters are estimated by using the specified algorithms.

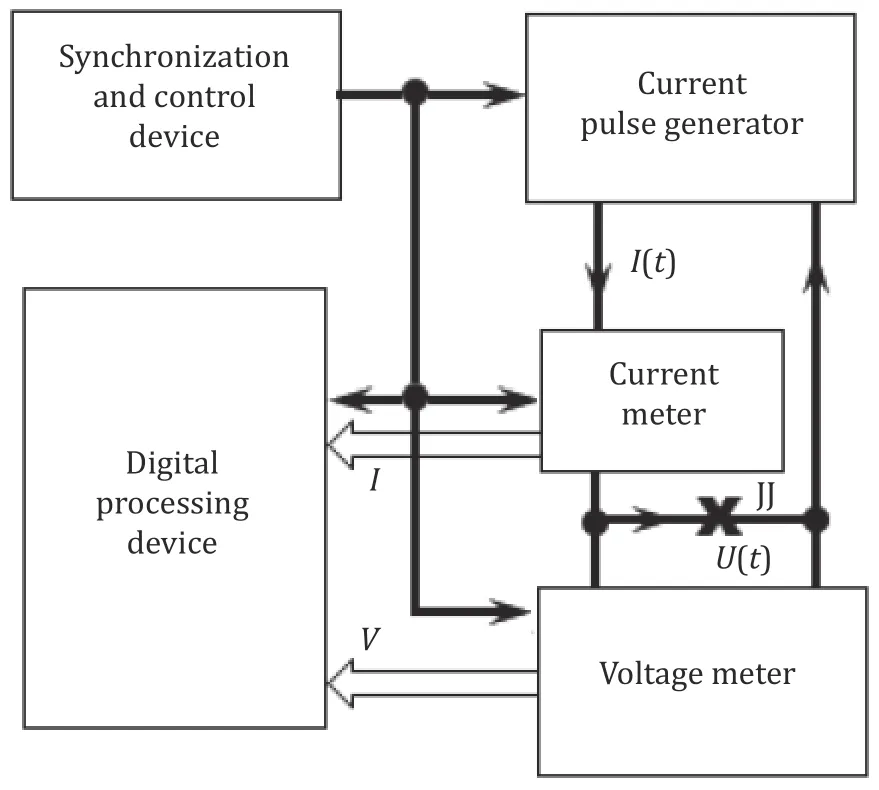
Fig.2.Structure of an automatic system for measuring DC parameters by IVCs of JJ.

A packet of symmetrical triangular current pulsesIS(t) which have slowly rising and falling edges and a pulse ratio of 1.5 is employed as the test signal (Fig.3):

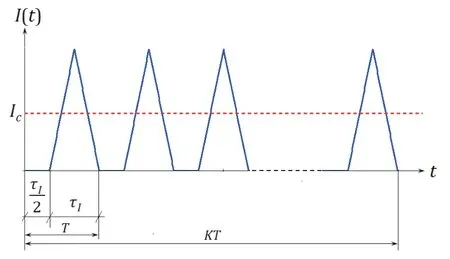
Fig.3.A packet of symmetrical triangular current pulses.

whereτIis the pulse base length,Tis the pulse period,k=1,2,…,K,vIis the current rising/falling rate,and=0.5vIτIis the current pulse amplitude.

The actual test signal is an additive mixture of the generated current pulse packet and a random componentξI(t):

whereξI(t) is a stationary Gaussian random process with a zero mean and a variance of.The pauses between pulses are to return JJ to the superconducting state and used as the reference intervals containing only noise readings when the algorithms are constructed to detect breaks in IVC.Considering that the proposed algorithms focus on digital measuring systems,the pulse base lengthτI=2Mτd,whereM>1 is an integer.The pulse period is equal toT=3Mτd.

The piecewise linear approximation of SIS-type hysteretic underdamped JJ IVC is applied.It is determined by the five above-mentioned parameters.With increasing and decreasing currents,IVC approximation takes the following respective forms:

Since the current is a composition of a random process and deterministic one,the voltage as a function of time is also a random process.According to (1)–(3),the timing diagram of the voltageU(t) at JJ takes the form shown in Fig.4,when driven by a symmetrical triangular current pulseI0(t)containing a random component.Moreover,a random error is also introduced into the measurement result by the current and voltage meters due to the intrinsic noise of the electronic components.

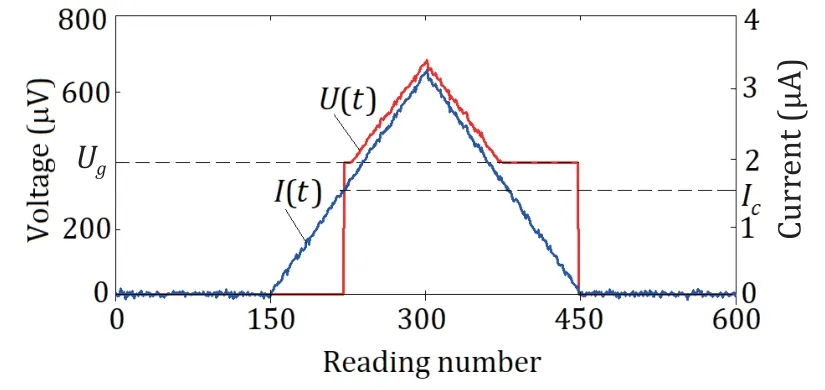
Fig.4.Timing diagram of the voltage at the SIS-type JJ driven by a symmetrical triangular current pulse containing a random component.

Assume that the intrinsic noise of a current meter and that of a voltage meter are also Gaussian processes,which are denoted byηA(t) andηV(t),with a zero mean value and,in the general case,with unknown variances of,respectively.The algorithms are synthesized to measure the parameters for the case of.Then the influence of the current measurement error in the measured results of the JJ parameters is investigated.Initial data for the algorithm synthesis is the synchronous readings of the current and the voltage taken within the current pulse packet length with a fixed periodτd.Denote the voltage and current readings asViandIi,i=1,2,…,3MK,respectively.Within thekth pulse period,the firstMcurrent readings have a zero value,the followingMreadings correspond to the rising sections of the current pulse,and the remainingMreadings correspond to the falling sections of the pulse.

3 Checking the operability of the Josephson junction

When manufacturing JJs,several reasons may lead to defective products,resulting in these JJs out of operation.The most common faults include dielectric breakdown and shunting in the junction.The most prominent sign of these faults is the absence of a voltage jump on the junction when the bias current reaches a critical value.Therefore,if the voltage jump is not observed when measuring IVC,a decision should be made about the JJ failure.

The problem of detecting the voltage jump on JJ at the time (3M(k-1)+M+i)τdis equivalent to the problem of testing statistical hypotheses regarding the non-centrality parameter to the Student’st-distribution:

The most powerful unbiased algorithm used to solve the problem (5) takes the following equivalent forms [40]:

4 Critical current measurement algorithm

5 Leakage resistance measurement algorithm

To measure the leakage resistanceRlg,the voltage and current readings corresponding to the falling edges of the current pulses are used.In accordance with IVC,while the current passing through JJ decreases fromIcto almost zero,its corresponding voltage remains constant and equalsVg(Fig.4).Correspondingly,the average value of the measured voltage readings at the time points (3Mk-)τdis equal to the gap voltageVg,i.e.,=Vg.First,the readings corresponding to the falling segments of the current pulses are determined,at which the voltage across the junction drops fromVgto 0.Then the algorithm is synthesized to estimateRlg.

The reading numbers corresponding to the falling edge of the voltage are determined in two stages.In the first stage,readings with the average value less than the gap voltageare detected.The algorithmφ1(⋅) applied to detect such readings is similar to (6):

In the second stage,at the falling edge of the voltage,the voltage readings with the average values of>0 are determined.The algorithmφ2(⋅) used to detect such readings is obtained similarly to the way doing at the first stage,with the following form:

To synthesize the algorithm for theRlgestimation,suppose that the measurements of the values of the current readings are accurate.Then,the effect of current measurement errors on the total error in measuring the leakage resistance is evaluated.SinceRlgis quite large,which is 30–40 times or more larger than the normal junction resistanceRN,then,at a fixed sampling period,the current falling rate in the pulse,determined by the length of the falling edge,is selected such that the falling section accounts for at least two sampling periods.Since the current falling rate at a fixed sampling period is determined by the number of the readingsMat the falling edge of the pulse,Mmust satisfy the inequalityM≥2ImaxRlg/Vg.Preliminarily,Mcan be estimated by assuming,for example,thatImax=5Ic,and using the parameters ofIc,Rlg,andVgobtained at the design stage of JJ.This value ofMcorresponds to the minimal error rate of the parameter estimation,as shown in Section 7.

By denotingZ+as the vector composed of the non-zero components of the vectorZ,the conditional probability density function (PDF) of the vectorZ+has the following form:

To obtain the estimate ofRlg,the estimation technique proposed in Ref.[41] is used.First,the desired parameter is expressed in terms of the mathematical expectation of the statisticsT2.Second,the mathematical expectation is substituted with the value of the complete sufficient statisticsT2in the resulted expression.The resulted estimate has a minimum variance [42]; the simulation method will be further applied to estimate the bias magnitude.In the absence of bias,the estimate is efficient.

The mathematical expectation of the statisticsT2has the following form:

The desired measurement valueof the leakage resistance is achieved by solving (11) with respect toRlgand substitutingE(T2) with the statisticsT2value:

6 Algorithms for measuring the parameters of RRRNNN,IIIggg,and VVVggg

To synthesize algorithms for measuring the parameters ofRN,Ig,andVg,it is necessary to determine the numbers of the current and voltage readings corresponding to the IVC segment where the voltage at the junction is larger thanVg.

By applying the same approach as that in the synthesis of the algorithms (6),(8),and (9),the most powerful unbiased algorithms are obtained to make the decision whether the magnitudes>0,i.e.,JJ is in the normal state,at the time points (3Mk-M-lk)τdand (3Mk-M+nk)τd:

where

withjk=3M(k-1)+1,3M(k-1)+2,…,3M(k-1)+Mandk=1,2,…,K.The threshold constantC(α)=t(1-α),(M-1)is still defined as the (1-α) level quantile of Student’st-distribution.

The vector of parametersΘ=[ϑ1,ϑ2,ϑ3,ϑ4]Ttakes values from the 4-dimensional interval(-∞,0)×(0,∞)×(-∞,∞)×(0,∞) since the parametersσV,RN,Vg,andIgcan take arbitrary values.Therefore,the sufficient statistics are complete [40].By applying the technique proposed in Ref.[41],a system of equations is compiled to express the desired parameters in terms of the mathematical expectations of complete sufficient statistics:

By solving (18)–(20) and substituting the mathematical expectations with the values of complete sufficient statistics,the estimates of the desired parameters can be obtained as

7 Simulation results

The performance of the proposed algorithm is analyzed through Monte Carlo computer simulations.By using MATLAB,the synchronous voltage and current readings at the measuring unit output (Fig.2) are simulated with various parameters of the current pulse generator and the standard deviations (root-mean-square errors) of the voltage and current meters.The following values of the JJ parameters are adopted as the initial data:Ic=1.8 μА,Imax=2.12Ic,andVg=365 μV which are taken from Ref.[39];RN=150 Ω;Rlg=4.5 kΩ;Ig=1.98 μА.The sampling period is assumed to be constant throughout all experiments and equal toτd=0.25 ms,which corresponds to the current pulse generator bandwidth of 2 kHz.To investigate the performance of the proposed algorithms,the relative total error is used to measure the JJ electric parameters:

The dependence of the relative total error (24) on the following parameters is estimated: The normalized standard deviation of the random component of the current readings generated by the current pulse generatorδI=σI/Ic,the normalized root-mean-square error of the current meterδA=σA/Ic,the normalized root-mean-square error of the voltage meterδV=σV/Vg,the number of pulsesKin the packet,and the number of readingsMwithin the length of the rising/falling edge of a pulse.It is assumed that all errors obey the Gaussian distribution.The measurement errors caused by current and voltage meters have a zero mean.The average values of current readings are determined by the current values at the current generator output.

First,it is noted that once the current and voltage readings (the ideal meters) are accurately measured,the resulted measurements of all parameters,except for the critical current,do not contain errors.In this case,the error in measuring the critical current is determined by the discrete nature of the readings.In the absence of current fluctuations,the maximum valueof the relative error in measuringIcis equal to half of that in the current quantization step,i.e.,=Imax/(2MIc).The presence of current fluctuations increases the measurement error.The dependence of the relative total errorin measuring the critical current on the relative standard deviation of fluctuations of the current generator and current meter has been obtained in Ref.[39].The measurement error depends on the standard deviation of current fluctuations and has a local minimum,which becomes less pronounced as the valueMincreases.In the range from 0.01δIto 0.02δI,the dependence is close to each other.The current meter noise with a relative standard deviationδA=0.003 increases the critical current measurement error by no more than 0.16% in the range from 0.005δItoδI.

Fig.6 shows the dependence of the relative total errorsin the measurements ofRlg,Ic,RN,andIgon the ratioγ=δA/δIwith fixed valuesδV=0,δI=0.02,K=50,andM=250.The total deviation of theVgmeasurement herein remains equal to zero.

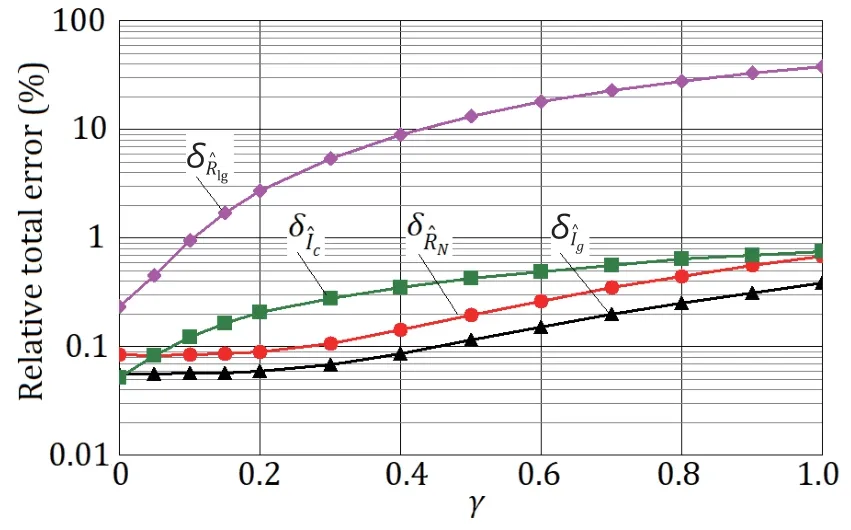
Fig.6.Dependence of the relative total errors of the parameter measurements of Rlg,Ic,RN,and Ig on the ratio γ of the standard deviation of the current meter to the standard deviation of the current random component for error-free measurements of the voltage readings with K=50,M=250,and δI=0.02.

As shown in Fig.6,the measurement error in the current readings leads to an error in the parameter measurements ofIg,RN,andRlg,and increases the error in measuring the critical current by approximately 0.7% when the standard deviation of the current is equal to that of the current meter(γ=1).The largest total error in the measurement of the resistanceRlgis observed.Forγ≤0.15,the total error in measuringRlgdoes not exceed 2%; for the other parameters,it remains less than 0.2%.

The presence of an error in the voltage meter also leads to an additional increase in the total error when measuring each of the JJ parameters,except forIc.Fig.7 presents the dependence of the relative total errorsin the measurements ofRlg,Ic,RN,Ig,andVgon the relative standard deviationδIof the current generator fluctuations at relative standard errorsδA=0.003 andδV=0.015 of the current meter and the voltage meter,respectively,withK=50 andM=250.

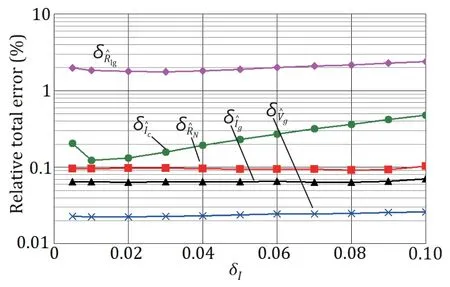
Fig.7.Dependence of the relative total errors in the parameter measurements of Rlg,Ic,RN,Ig,and Vg on the standard deviation of the current fluctuations with δA=0.003 ,δV=0.015,K=50,and M=250.

As shown in Fig.7,in the range ofδI<0.07,the total errors in the measurements of all parameters,except for the critical current,practically are independent on the level of current fluctuations.At the relative standard deviation of the voltage meterδV=0.015,the measurement errors ofRNandRlgincrease by 0.025% and 0.010%,respectively,while that ofIgpractically does not change,when compared with the error-free voltage measurements.

Fig.8 (a) shows the dependence of the relative total error in the parameter measurements ofRlg,Ic,RN,Ig,andVgon the number of the current pulsesKin the packet withδI=0.02,δA=0.003,δV=0.015,andM=250.Fig.8 (b) shows their dependence on the number of readingsMwith the same values ofδI,δA,andδVwhileK=50.

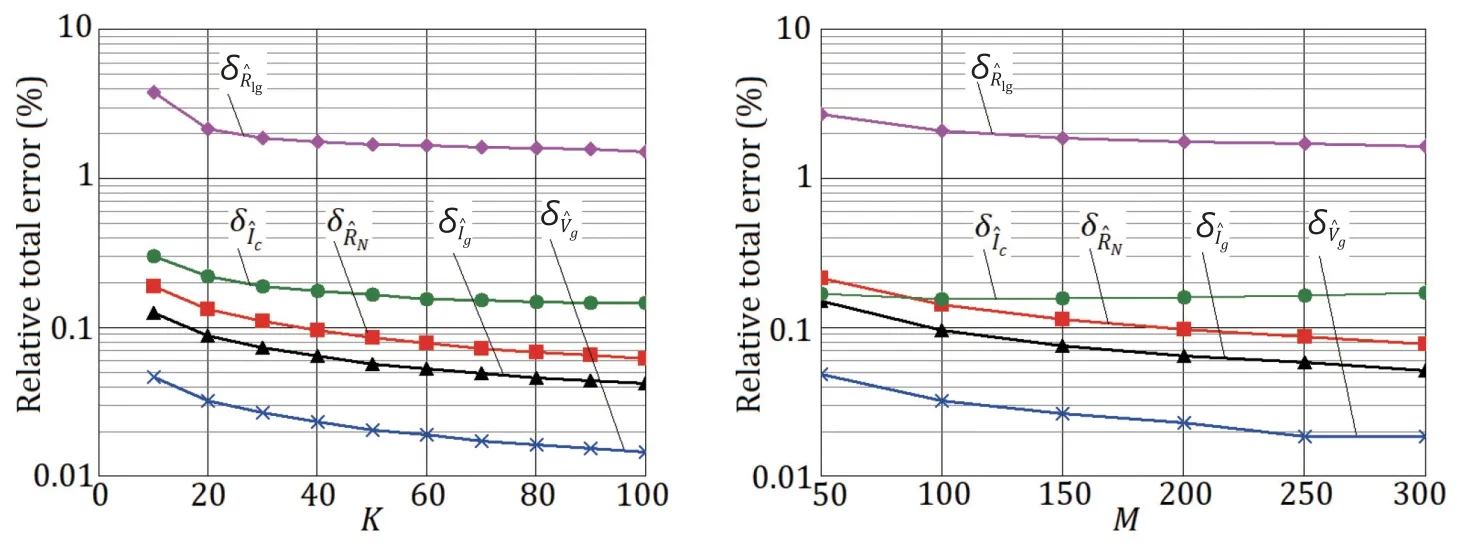
Fig.8.Dependence of the relative total errors in the parameter measurements of Rlg,Ic,RN,Ig,and Vg with δI=0.02,δA=0.003,and δV=0.015 on: (а) the number of pulses K in the packet with M=250 and (b) the number of readings M with K=50.

The dependence of errors in the parameter measurements ofRN,Ig,andVgon the number of pulsesKin the packet and on the number of readingsMhas the forms of,respectively,and the error decrease in the parameter measurements ofRlgandIcwith increasingKandMoccurs at a significantly slower rate whenK≥50.

8 Summary and conclusion

The algorithms have been proposed to measure the parameters of the SIS-type hysteretic underdamped JJs by automatic digital measuring systems.The piecewise linear approximation of JJ IVC is applied,which is determined by the five electrical parameters of the junction including the critical currentIc,the gap voltageVg,the maximal currentIg,and the leakage resistanceRlg.These parameters are estimated by the proposed algorithms.The synthesis method of the most powerful unbiased signal detection algorithms is used to determine the breakpoints of IVC.This approach is relevant since the transition of JJ from the superconducting state to the normal state and vice versa is characterized by a significant change in the voltage at JJ.This change is much higher than the noise level in the system.To overcome a priori uncertainty of the noise variance,the contrast method is applied.The pauses between pulses are used as the reference intervals containing only noise readings when the algorithms are constructed to detect breaks in IVC.This allows automatic adaptation of the algorithms to the background component parameters.

The parametersRlg,RN,Ig,andVghave been estimated by solving a system of equations composed of the expressions for the first initial moments of complete sufficient statistics,followed by substituting the true moments with complete sufficient statistics.When the desired parameter constitutes a linear combination of the moments of complete sufficient statistics,such an approach provides an efficient (unbiased and with the minimum value of the quadratic loss function) and essentially unique estimate of the parameter [42].In our case,such an estimate is the estimate of the parameterVg.For the parametersRlg,RN,andIg,the dependence on the initial moments has turned out to be nonlinear.Thus the obtained estimates may be biased.However,it minimizes the quadratic loss function in class of estimates with this bias and is essentially unique [43].Therefore,the relative total error (24) is used to characterize the accuracy of the estimates.

The simulation results show that the proposed algorithms used to estimate the electrical parameters have relative total errors of less than 1% in estimating all parameters when the employed measuring equipment has an error rate of 0.3% for the current measurement and 1.5% for the voltage measurement.The exception is the estimate of the leakage resistance,the total relative error of which can be ensured at the level of 1%–2%.An essential advantage of the proposed algorithms is the independence of their structures on the actual noise levels of the current pulse generator and the intrinsic noise of the current and voltage meters.The algorithms can be implemented in automatic digital measuring systems since only synchronous voltage and current readings at JJ in the test signal interval are required.

The universe approach has been proposed to synthesize algorithms for the automatic measurement under noise conditions.To create the algorithm,all you need are a mathematical model to measure parameters and a noise probability model.If the JJ type is uncertain,a database of expected IVC forms should be first created.Then,an appropriate IVC model should be identified from this database,for example,using the technique of testing multi-alternative hypotheses.Finally,the corresponding measurement algorithm can be applied.

For example,it is known that,for aluminum (Al) SIS-type junctions at mK-level temperatures,IVC back-bending can occur due to sample overheating when switching into the resistive state (Fig.2 (a) in Ref.[7]).Overheating depends on the measurement duration,the thermalization quality of JJ,the normal resistance value,and the current flowing through the junction.The measurement can be performed in two steps if it is not known whether JJ has been overheated.In the first stage,the test signal (1) is applied to JJ and a set of the synchronous readings of the voltage values and the corresponding readings of the current values is formed (see Section 4).Then,by using the algorithm (7),the critical current and defined numbers of readings corresponding to the expected flat part of IVC at the falling edge of each pulse of the test signal are measured.If the mean values of these corresponding readings averaged on all pulses of the test signal statistically differ,then overheating occurs.If the analytical form of IVC back-bending is unknown,only the readings corresponding to the rising edges of the current pulses of the test signal can be used,and the measurement of a leakage resistance becomes unavailable.

Funding

This work was supported by the Ministry of Science and Higher Education of the Russian Federation under Grant No.FSUN-2023-0007.

Declaration of competing interest

The authors declare no conflicts of interest.