Life-cycle assessment of batteries for peak demand reduction
Dylon Ho Cheng Lm,Yun Seng Lim,Jinhui Wong,Siti Ndih M.Spihie
a Department of Electrical and Electronic Engineering,Universiti Tunku Abdul Rahman,Kajang,43000,Malaysia
b Group Research & Technology Division,PETRONAS,Bandar Baru Bangi,43650,Malaysia
Keywords:Degradation estimation Maximum net savings Peak demand reduction State of health (SOH) estimation
ABSTRACT At present,a life-cycle assessment of energy storage systems (ESSs) is not widely available in the literature.Such an assessment is increasingly vital nowadays as ESS is recognized as one of the important equipment in power systems to reduce peak demands for deferring or avoiding augmentation in the network and power generation.As the battery cost is still very high at present,a comprehensive assessment is necessary to determine the optimum ESS capacity so that the maximum financial gain is achievable at the end of the batteries’lifespan.Therefore,an effective life-cycle assessment is proposed in this paper to show how the optimum ESS capacity can be determined such that the maximum net financial gain is achievable at the end of the batteries’ lifespan when ESS is used to perform peak demand reductions for the customer or utility companies.The findings reveal the positive financial viability of ESS on the power grid,otherwise the projection of the financial viability is often seemingly poor due to the high battery cost with a short battery lifespan.An improved battery degradation model is used in this assessment,which can simulate the battery degradation accurately in a situation whereby the charging current,discharging current,and temperature of the batteries are intermittent on a site during peak demand reductions.This assessment is crucial to determine the maximum financial benefits brought by ESS.
1 Introduction
The peak demand reduction is a critical criterion to ensure the network stability as well as reliability of electricity supply [1–3].Energy storage systems (ESSs) using lithium-ion (Li-ion) batteries are one of the recent proposed solutions for peak demand reductions [4,5].ESS can store excess electricity during lowdemand periods and discharge electricity during high-demand periods,effectively reducing the strain on the power grids and hence deferring the needs of network upgrade and additional generation capacity.With the appropriate battery capacity,a commercial customer can save up to USD 4000 in electricity bills annually.The utility company can save up to USD 21000 and avoid up to 16 tons of CO2annually [1].However,the operation of ESS for peak demand reductions involves frequent charging and discharging cycles,causing the battery to degrade rapidly and hence affecting the overall performance and lifespan of ESS.An accurate life-cycle assessment is therefore necessary in this commercial aspect because the optimum capacity of the batteries can be determined to achieve the maximum financial benefits to the utility companies and customers.
The battery degrades due to the loss of lithium inventory,active material decomposition,and structure changes [6,7].Different characteristics of the discharging current,charging current,temperature,and depth of discharge (DOD) of the batteries can cause the battery degradation differently [8].Hence,the battery lifespan will be affected differently.However,many existing battery models are not able to predict the degradation due to the different characteristics of the discharging current,charging current,and temperature.Most existing battery models can only be used with their specific limitations.For example,the empirical model proposed by Sarasketa-Zabala et al.[9] only considered DOD and cumulative usage capacity(Ah) in the degradation model.Wang et al.[10] proposed the degradation model that only considered the constant temperature,DOD,and discharging current.Peterson et al.[11] estimated the battery degradation based on the discharged capacity only.Han et al.[12] presented a generic model based on the constant discharging current and DOD only.Other empirical models only considered constant charging and discharging currents [13,14],or specific currents such as 0.7C,1C,and 2C by Diao et al.[15] and 1C,2C,and 5C by Chen et al.[16].In addition,the degradation does not include the idling degradation at all.The temperature and state of charge (SOC) over time are the primary factors that affect the idling degradation [17].All these degradation models are not suitable to be used to carry out a comprehensive life-cycle assessment for the batteries in ESS for peak demand reductions.
Recently,a comprehensive degradation model,known as the characteristic-based degradation model,is proposed in Ref.[18].This model can simulate the battery degradation with different characteristics including the charging current,discharging current,battery temperature,and DOD.The model accuracy is well verified.In this paper,a comprehensive life-cycle assessment is presented to determine the optimum capacity of ESS to achieve the maximum financial gain by the utility companies and customers when used for peak demand reductions.All the case studies show exactly how the optimum size of ESS is determined on a particular site under the given commercial framework of electricity trading.The battery degradation model is an important component in this life-cycle assessment as it can accurately predict the battery lifespan based on how the batteries are charged and discharged together with the temperature the batteries are subject to.In the sensitivity analysis,it is demonstrated that the results of the life-cycle assessments are still accurate and valid even if the battery degradation model is calibrated with some errors.
A comparative analysis of this research work with other related studies [14–16,18] is carried out and shown in Table 1,which highlights several novelties of the proposed model in this work.Specifically,the battery degradation model proposed in this paper accounts for idling degradation,which has not been considered in the other studies.Furthermore,the different characteristics of the discharging current,charging current,and temperature are explored in this paper.In Ref.[18],instantaneous discharging and charging currents are addressed,but the temperature is assumed to be constant at 30 °C.Reference [15]presents the battery degradation model with the discharging current and charging current being fixed at a particular C-rate in each time with a constant temperature,where the C-rate is defined as the time required to fully charge or discharge a battery.Similarly,Ref.[16] only focuses on the battery degradation with a constant C-rate of 1C,2C,and 5C and a constant temperature of 25 °C,45 °C,and 55 °C,respectively.In comparison,the battery degradation model proposed in this paper considers the instantaneous changes in the discharging current,charging current,and temperature over time.In addition,such a comprehensive battery model is used in the life-cycle assessment for the first time to evaluate the financial viability of ESS,providing new and valuable information with regard to the commercial aspects of ESS.

Table 1 Comparative analysis of the proposed model in this work with other related models.
At present,a comprehensive life-cycle assessment of ESS is not available in the literature as shown in Table 1.This life-cycle assessment is increasingly vital nowadays as ESS is recognized as one of the essential components in power systems to reduce peak demands for improving the affordability of electricity.As the battery cost is still very high at present with a short lifespan,this comprehensive assessment is proposed and presented in this paper to determine the optimum ESS capacity to achieve satisfactory net financial gain for the utility companies or customers,otherwise ESS may remain as a pessimistic solution.The assessment results accurately reflect the financial performance of ESS over its lifespan.Such findings should be made available in the public domain because the government,policy makers,and utility companies can understand the potential benefits and contribution of ESS towards the affordability of electricity and environmental sustainability.As a result,appropriate regulatory and commercial frameworks for the ESS deployment can be developed for the country.
The remainder of this paper is organized as follows.Section 2 describes the characteristic-based battery model used for the life-cycle assessment.Section 3 explains the methodology of the life-cycle assessment.Section 4 shows how the degradation is calculated with an instantaneous discharging current or a constant discharging current.Section 5 compares the battery degradation under an instantaneous battery temperature and a constant battery temperature.Section 6 presents a sensitivity analysis to show the robustness of the assessment against different calibration errors.Section 7 shows how the life-cycle assessment determines the optimal ESS capacity for the maximum net savings in peak demand reduction applications.Finally,this paper is concluded in Section 8.
2 Proposed characteristic-based battery model for the life-cycle assessment
A comprehensive approach is developed and presented in this paper to show how the optimum ESS capacity can be determined to achieve satisfactory financial gain for power utility companies or customers.The proposed approach uses a versatile battery degradation model to simulate and determine the battery lifespan accurately under the instantaneous charging current,discharging current,and temperature.Many existing battery models cannot determine the battery degradation accurately because they do not consider all the three instantaneous charging current,discharging current,and temperature simultaneously as shown in Table 1.In the following subsections,the simplified version of the degradation model as proposed in Ref.[18]is described.Then the total battery degradation due to the discharging current and idling is presented.The procedure for calibrating the model is also briefly described.
2.1 Degradation caused by charging and discharging
In the battery model,the daily discharging and charging degradation exponentϵdis,chg(n) on thenth day represents the impact of the discharging and charging cycles on the battery degradation [18].This value,along with the daily idling degradation exponent valueϵidle(n),is used to calculate the total battery degradation.The battery degradation during discharging and charging is primarily influenced by four main factors: Discharging current,charging current,temperature,and DOD.In the battery model,they are represented by the degradation factorsθI,dis(n),θI,chg(n),θT(n),andθDOD(n),respectively.These degradation factors are derived from the life-cycle model proposed in Ref.[14],which originally calculates the battery lifespan based on a constant discharging current,charging current,battery temperature,and DOD for continuous discharging and charging cycles.However,in peak demand reduction applications where the discharging current and battery temperature vary over time,the original model in Ref.[14] is not applicable.Therefore,this paper modifies it by considering the instantaneous changes in the discharging current and battery temperature at each minute.
The impact of the discharging current on the battery degradation is represented by the daily discharging current degradation factorθI,dis(n).Since the discharging current fluctuates during peak demand reduction applications,the instantaneous discharging current degradation factorθI,dis(t) at the minutetis calculated at every minute using the measured instantaneous discharging current values.The sum of allθI,dis(t) values throughout the discharging period givesθI,dis(n).The equations forθI,dis(n) andθI,dis(t) are as follows:
wheretdisis the total time of the discharging period in minutes (min),Idis(t) is the discharging current at the minutet(C-rate),Idis,refis the reference discharging current (C-rate),andγ1is the calibrated coefficient for the discharging current.
The impact of the charging current on the battery degradation is represented by the daily charging current degradation factorθI,chg(n).In peak demand reduction applications,the battery charging current is typically constant and does not fluctuate.The battery is charged slowly at a low and constant current during off-peak hours to minimize the battery degradation.Therefore,θI,chg(n) only needs to be calculated once each day.The equation forθI,chg(n) is
whereIchg(n) is the charging current at thenth day (C-rate),Ichg,refis the reference charging current (C-rate),andγ2is the calibrated coefficient for the charging current.
The impact of the battery temperature on the degradation is represented by the daily temperature degradation factorθT(n).The battery temperature is influenced by the ambient temperature and output current.During idling periods,the battery temperature is similar to the ambient temperature,but it increases proportionally with the output current magnitude when the battery is charged or discharged.These fluctuations in the battery temperature are considered by using the instantaneous temperature degradation factorθT(t) which is calculated at every minute.The equations forθT(n) andθT(t) are as follows:
wheretdis,chgis the total time of the discharging and charging cycles in minutes (min),T(t) is the instantaneous battery temperature at the minutet(K),Trefis the reference battery temperature (K),andψis the calibrated coefficient for the battery temperature.
The impact of DOD on the battery degradation is represented by the daily DOD degradation factorθDOD(n).DOD is defined as the percentage of the battery’s discharged capacity relative to its overall capacity.The DOD value on thenth day DOD(n) andθDOD(n) are calculated by
where DODrefis the reference DOD (p.u.),ξis the calibrated coefficient for DOD,and SOC(n) is the minimum SOC value of the battery at the end of the discharging cycle (p.u.).For example,a battery that is discharged from 100%-SOC to 20%-SOC will have a DOD(n) value of 0.8.Since DOD(n) is calculated at the lowest point of the battery’s SOC at the end of each discharging cycle,there is only one DOD value for each day.
The batteries are discharged to supply power to the loads to reduce peak demands from the grid during day time and then charged during night time,hence making the batteries undergo a complete discharging and charging cycle per day.If the battery is discharged starting from 100%-SOC and then charged back to 100%-SOC,then this cycle is considered as a complete discharging and charging cycle.If the starting SOC before discharging or the ending SOC after charging is lower than 100%,then this cycle is considered as an incomplete discharging and charging cycle.The parameterNeqis used to account for the completion degree of discharging and charging cycles.For complete discharging and charging cycles,Neq=1.For incomplete discharging and charging cycles,Neqis calculated by
where DODstart(n) and DODend(n) are the DOD values at the start and end of the cycle,respectively.They can be calculated as follows:
where SOCstart(n) and SOCend(n) are the SOC values at the start of the discharging cycle and the end of the charging cycle,respectively (p.u.).
After all the degradation factors are calculated,the daily discharging and charging degradation exponentϵdis,chg(n) is calculated by
whereNc,refis the reference cycle life of the battery given in the battery datasheet.
2.2 Degradation caused by idling
In peak demand reduction applications,the battery is idle during the days when the load is low,such as weekends and public holidays [19].During this period,the battery is neither discharged nor charged.The impact of the idling period during these inactive days on the battery degradation is represented by the daily idling degradation exponentϵidle(n).The battery degradation that occurs during idling is mainly affected by the battery SOC and temperature.During idling,the battery temperature is similar to the ambient temperature and follows the changes in the ambient temperature throughout the day.Therefore,the instantaneous idling degradation exponentϵidle(t) is used to consider the changes in the battery temperature at every minute.The daily idling degradation exponentϵidle(n) is then calculated by taking the sum of all theϵidle(t) values throughout the day.Theϵidle(n) andϵidle(t) values are calculated as follows:
wheretidleis the idling period of the battery in minutes (min),W0is the parameter of the Lambert function,A′is the pre-exponential factor (p.u./min),Eais the activation energy (eV),kis the Boltzmann constant (eV/K),Bis the fitted parameter of the idling degradation equation,SOC(t) is the battery SOC at the timet(p.u.),andzis the parameter of the capacity loss function.
The equations for the idling degradation exponent are based on the idling degradation model proposed in Ref.[19].The original idling degradation model calculates the idling degradation when the battery is stored at a constant temperature.It does not consider the changes in the battery temperature during idling.Therefore,they are modified in this paper by taking the changes in the battery temperature at every minute into consideration.All the parameters are calibrated against Li-ion batteries and are given in Table 2.Further explanations related with these parameters can be found in Ref.[19].

Table 2 Parameters for the idling degradation equations.
2.3 Total battery degradation
After all theϵdis,chg(n) andϵidle(n) values are calculated for each day,the total degradation exponentϵtotalis calculated by
wherendis,chgandnidleare the numbers of the days that the battery carries out peak demand reductions and the battery is idle,respectively.
The battery degradation exhibits a non-linear characteristic over time.The degradation is slower when the battery is new and then accelerates as the battery ages.This degradation pattern is due to the chemical properties of the battery,which changes non-linearly as the battery ages.Therefore,the non-linear aging exponentαis used to represent the non-linear characteristic of the battery degradation over time.The value ofαvaries depending on the battery type and is determined empirically.Based on the above parameters,the capacity loss of the batteryQlossis calculated by
whereQ100%is the battery capacity (Ah) when the state of health (SOH) is 100% andQEOLis the battery capacity (Ah) at the end of the cycle life as defined during calibration.
Then,the battery SOH after degradation is calculated as
whereQnomis the nominal capacity of the battery (Ah).
2.4 Procedure for calibrating the batteries
Before the model is used to calculate the battery degradation,it must first be calibrated against the physical battery.The calibration process can be carried out by using the parameters listed in the battery datasheet [18].If the required parameters cannot be found in the battery datasheet,they also can be obtained empirically.The calibration procedures are as follows:
i) Determine the first set of the reference discharging current (Idis,ref),reference charging current (Ichg,ref),reference battery temperature (Tref),reference DOD (DODref),and the corresponding cycle life (Nc,ref) when the battery is cycled using the reference parameters.The reference values of these parameters (Idis,ref,Ichg,ref,Tref,and DODref) are selected based on the nominal or rated values given in the battery datasheet.The batteries are charged and discharged repeatedly atIdis,ref,Ichg,ref,Tref,and DODref.The number of cycles that the battery takes to drop its SOH from 100% to 90% is recorded asNc,ref.
ii) Determine the second set of the reference parametersIdis,ref2,Ichg,ref2,Tref2,and DODref2.The values for the second set of these reference parameters should be different from the first set of the reference parametersIdis,ref,Ichg,ref,Tref,and DODref.Then,the batteries should be cycled again with one of the parameters using the second reference value and the other three parameters keeping the original reference values.The corresponding cycle life is then recorded.For example,to obtain the corresponding cycle lifeNc,Idisfor the second reference discharging currentIdis,ref2,the battery is cycled by using the parametersIdis,ref2,Ichg,ref,Tref,and DODref.This step is repeated to find the values for the cycle lifeNc,Ichg,Nc,T,andNc,DOD.All the reference parameters along with their corresponding cycle life are listed in Table 3.

Table 3 Reference parameters and their corresponding cycle life.
iii) After all the reference parameters and the corresponding cycle life are determined,the coefficientsγ1,γ2,ξ,andψare calibrated by using the following equations:
iv) After the coefficientsγ1,γ2,ξ,andψare calibrated.The calibration process of the battery model is completed.The battery model can then be used to calculate the battery degradation using (1)–(20).
3 Methodology of life-cycle assessment
The flowchart of the life-cycle assessment,as shown in Fig.1,is described in this section.First,the suitable ESS capacity is selected based on the estimated capacity required for the peak demand reduction application.The corresponding cost of ESS is calculated.The maximum peak demand reduction savings that can be generated using ESS are calculated for every month and the charging and discharging strategy is determined.The battery model is then used to predict the battery degradation that will occur based on the operation strategy.From the predicted battery degradation,the battery lifespan is calculated along with the corresponding net savings that can be generated over its service lifespan.Different ESS capacity is selected,and the previous steps are repeated to calculate the net savings for the new ESS capacity.The ESS capacity that can generate the highest net savings over its service lifespan will be the optimum ESS capacity for the peak demand reduction scenario.

Fig.1.Flowchart of the life-cycle assessment using the battery model.
4 Case 1: Battery degradation with an instantaneous/constant discharging current
Case 1 is carried out to show how the battery degradation can be affected by an instantaneous discharging current and a constant discharging current as represented by the scenarios 1a and 1b,respectively.In this case study,the 200-kWh ESS is charged and discharged with its SOC varying between 20% and 80% in a cycle before it is idle for next 24 hours.
The average value and total capacity (Ah) of the instantaneous discharging current of 1a are the same as those of 1b (see Fig.2 ).The average discharging current is 0.05C and the total discharged capacity is 120 Ah.The output current and SOC for the scenarios 1a and 1b are shown in Figs.2 and 3,respectively.
The required parameters for Case 1 are the discharging current,charging current,temperature,and DOD.For both scenarios,the charging current is 10 A and DOD is 0.8.The temperature is assumed to be 30 °C throughout the experiment.In the scenario 1a,the instantaneous discharging current varies with time and has an average value of 10 A,a minimum value of 0,and a peak value of 15.7 A.In the scenario 1b,the discharging current is 10 A.In both scenarios,ESS is idle for 24 h after the discharging and charging cycle.SOC of ESS during idling is 80%.Based on the above parameters,(1)–(15) are used to calculate the following parameters given in Table 4.

Table 4 Parameters used in Case 1.
Based on Table 4,it can be seen that there is a difference in the capacity loss between 1a and 1b even though the total discharged capacity is equal in both scenarios.When ESS is discharged with an instantaneous current,Qlossis 0.007961 Ah which is lower than that of 0.008017 Ah obtained with a constant current.In addition,it is noticed thatθI,dis(n) of 1a is lower than that of 1b even though the charging current,battery temperature,DOD,total charged energy,and total discharged energy are the same.The only difference between the two scenarios is that the discharging current is instantaneous in 1a and constant in 1b.Therefore,it can be concluded that the degradation discrepancy for these two scenarios is caused by the different profiles of the discharging current.
As mentioned in Section 1,most of the existing degradation models in literature did not consider this discrepancy.These existing degradation models only considered a constant or average current rather than the instantaneous current.This discrepancy can cause inaccuracy in the degradation estimation as most of ESSs used for peak demand reduction applications are discharged intermittently.Therefore,it is more efficient for the battery model to consider the instantaneous current rather than just the average or constant current.
5 Case 2: Battery degradation with an instantaneous/constant battery temperature
Case 2 is carried out to show the degradation affected by the instantaneous battery temperature and constant battery temperature,as described by the scenarios 2a and 2b,respectively.The battery temperature data over a nine-month period is collected.One-month data is shown in Fig.4.For weekdays,ESS is discharged during peak hours and charged during off-peak hours at night,causing the battery temperature to be high.On weekends and public holidays,the load is usually low.Therefore,ESS is idle during this period,making the battery temperature relatively low.When the battery is idle,the battery temperature is dependent on the ambient temperature.When the battery is charging or discharging,the battery temperature is affected by both the ambient temperature and output current.This means that a higher output current leads to a larger rise in the battery temperature.
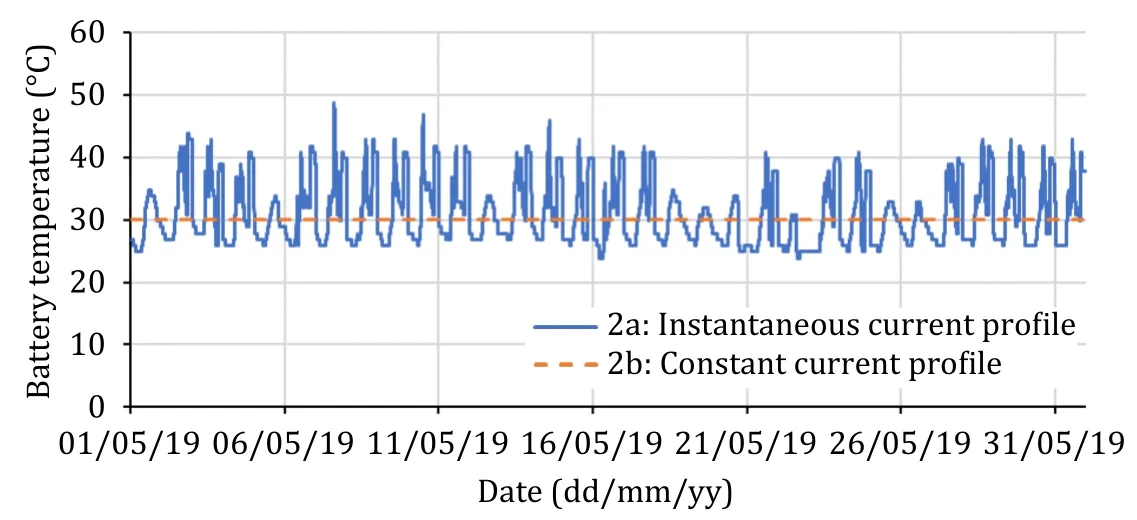
Fig.4.Changes in the battery temperature over a period of one month.
Fig.5 shows the changes in the battery temperature with time for a weekday and a weekend day.On the weekend,the battery is completely idle throughout the day,and the battery temperature is close to the ambient temperature ranging from 26 °C to 34 °C.Usually,the ambient temperature is high in the afternoon and then low early in the morning or night.During a weekday,the batteries are discharged during peak hours and charged during off-peak hours.During peak hours,the battery temperature can rise possibly to the highest of 42 °C.During off-peak hours,the battery temperature can drop possibly to the lowest of 26 °C.On the weekday,the battery temperature during charging reaches up to 42 °C.However,the battery temperature varies from day to day depending on both the ambient temperature and the output current.A summary of the battery temperature during the nine-month period is given in Table 5.The average battery temperature is found to be 30 °C,which is close to the average daily temperature in Malaysia.The maximum battery temperature is 51 °C,which is still within the safe operation range stated in the battery datasheet.

Fig.5.Example of the battery temperature variations during a weekday and a weekend day.

Table 5 Summary of the battery temperature over the nine-month period.
In 2a,the instantaneous battery temperature is recorded every minute and used as the input to the battery model.While in 2b,a constant battery temperature of 31 °C is used,even though in the actual scenario,the battery temperature varies from 23 °C up to 51 °C depending on the time of the day.All other inputs of the battery model,such as the discharging current,charging current,DOD,and SOC,are equal in these two scenarios.The capacity losses for 2a and 2b over the nine-month period are shown in Fig.6.Obviously in 2a,the capacity loss after nine months is calculated to be 6.3 Ah,whereas in 2b,the calculated capacity loss is 7.3 Ah.This capacity loss is extrapolated by the battery lifespan from 100%-SOH to 80%-SOH.The change in SOH over the battery lifespan is shown in Fig.7.When the battery degradation model considers the changes in the battery temperature at every minute,the estimated battery lifespan is about 7.1 years.However,most existing battery degradation models did not consider the changes in the battery temperature and assumed the temperature to be constant.When the battery degradation model assumes a constant battery temperature,the estimated battery lifespan is about 6.3 years.The difference is about 11% in the battery lifespan.Therefore,it can be concluded that the model using the instantaneous battery temperature is more feasible than the one using a constant battery temperature.

Fig.6.Comparison of the calculated capacity losses over time in 2a and 2b.

Fig.8.Comparison of the estimated SOH throughout the ESS lifespan when the calibrated coefficient values are varied.

Fig.9.Comparison of the SOH estimation error throughout the ESS lifespan when the calibrated coefficient values are varied.
6 Sensitivity analysis of the battery model
Although knowledge of the battery chemical characteristics is not required for the proposed battery model,it is still necessary to carry out experiments on the physical batteries to calibrate the model.Therefore,a sensitivity analysis is necessary in this case to evaluate the robustness of the simulation results due to the possible calibration errors being introduced to the model inadvertently.The degradation coefficients of batteries due to the instantaneous charging current,discharging current,and temperature are determined and incorporated in the sensitivity analysis to show that the battery model is robust against any small errors that may occur during the calibration process.The coefficient values of the discharging current(γ1),charging current (γ2),DOD (ξ),and temperature (ψ) are changed by ±5% from the reference values as given in Table 6.

Table 6 List of coefficients for each scenario.
The simulation results due to different coefficient values are shown in Figs.8 and 9.They indicate that the changes in the coefficient values do not impose any significant difference in the simulation results.It is therefore concluded that the simulation results are very robust towards the errors that may occur in the coefficient values during the simulation.
7 Net savings analysis for peak demand reductions of a university building
A life-cycle assessment is carried out to determine the optimal ESS capacity to achieve maximum net savings when ESS is used for peak demand reductions.The one-month load profile of the building for the Faculty of Medicine and Health Sciences at Universiti Tunku Abdul Rahman is collected and shown in Fig.10.The daily peak demand is not consistent throughout the month with 1.24 MW being the maximum demand and 300 kW being the lowest demand.
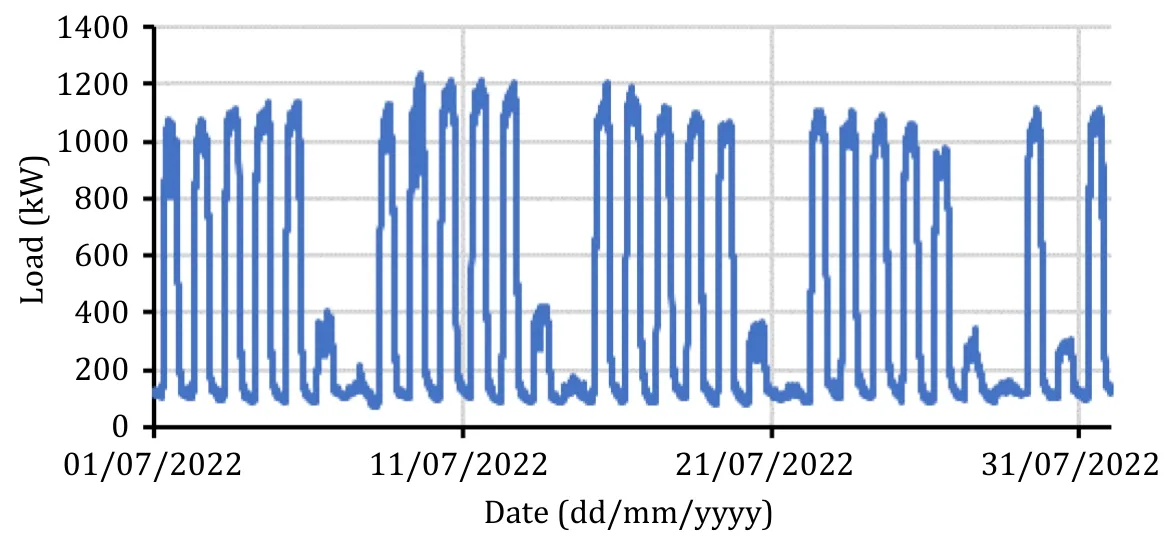
Fig.10.Load profile of the university building over a period of one month.
Fig.11 shows the power supply of ESS and the power supply by the grid when the ESS capacity is 381 kWh.It is noticed that the maximum power supply by the grid is reduced because ESS supplies the necessary power to the load such that the power demand from the grid is reduced.

Fig.11.Power supply of the 381-kWh ESS and power supply by the grid.
In this life-cycle assessment,the ESS capacity is varied from 27 kWh to 917 kWh.In each ESS capacity,the reduction in maximum demands,savings in electricity bills,and the cost of ESS are determined with the assumptions that SOH of the batteries is cycled between 100% and 60%.Table 7 shows the ESS capacity with the corresponding cost,lifespan,and the total savings.The battery lifespan is determined by using thesimulation model based on the discharging current profiles.The unit cost of ESS is 1250 MYR/kWh.The total savings are calculated based on the peak demand charges of 45 MYR/kW.
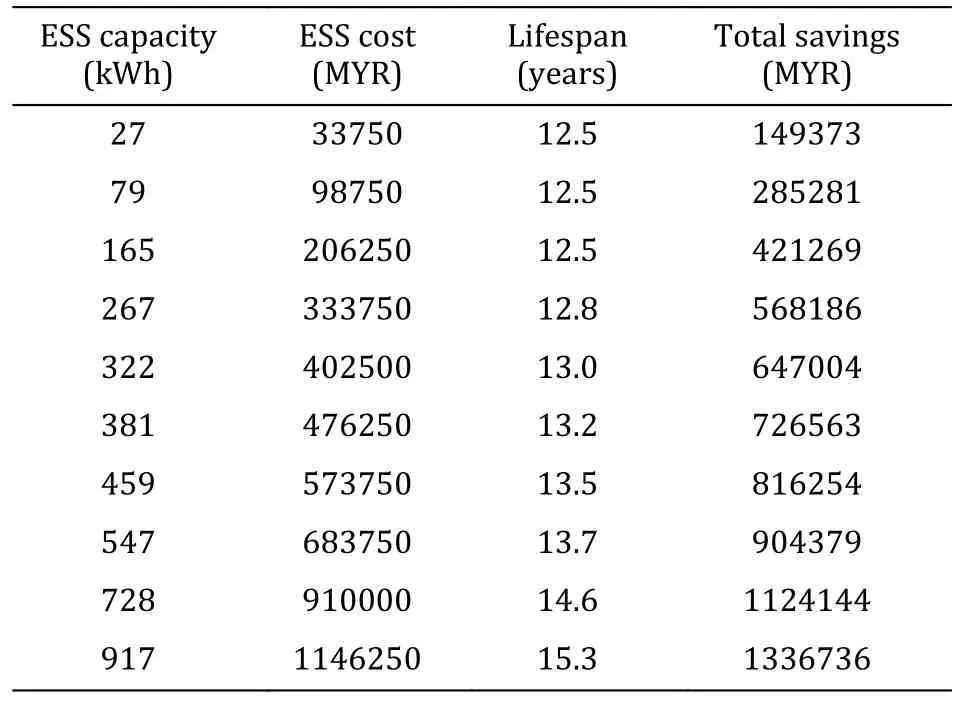
Table 7 Lifespan and total savings of each ESS capacity with its corresponding cost.
It is noticed that the ESS lifespan ranges from 12.5 years to 15.3 years.This lifespan is longer than the typical lifespan expected by Li-ion batteries mainly due to two factors: i) SOH of the batteries is cycled between 100% and 60% instead of 100% and 80% as typically seen in electric vehicle applications;ii) ESS stays in the idling state and only operates for a few days out of the whole month.The resulted net savings for each ESS capacity is shown in Fig.12.It is noticed that 381-kWh ESS provides the highest net saving of 250313 MYR.Therefore,381 kWh is the optimal ESS capacity to achieve the maximum net savings for peak demand reductions.

Fig.12.Comparison of net savings generated by each ESS capacity over its operational lifespan.
The findings on the life-cycle assessment suggest that it is financially viable to use ESS to reduce peak demands such that the affordability of electricity can be further improved.Such findings should be made available in the public domain because the government,policy makers,and utility companies can understand the potential benefits and contribution of ESS towards the affordability of electricity and environmental sustainability.As a result,appropriate regulatory and commercial frameworks for the ESS deployment can be developed for the country.
8 Conclusion
Power utility companies or energy providers have the obligation to provide a reliable electricity supply to customers.It is therefore necessary to carry out regular augmentation in electric networks and power generation to meet the increasing maximum power demands.The costs associated with the augmentation can be recovered by increasing the selling price of electricity.The economic growth is severely affected by the increased electricity prices especially in the poor and developing countries.ESS has been proposed recently to reduce the increasing maximum demands such that the needs of augmentation can be deferred or avoided.However,satisfactory cost savings can only be realized if a comprehensive approach,also known as life-cycle assessment,is developed and presented in this paper to determine the optimum ESS capacity for a grid service.Several case studies are carried out to show the financial gain by different ESS capacity.The optimum ESS capacity is the one that provides the maximum financial gain.
This paper presents a life-cycle assessment that determines the optimal ESS capacity that provides the maximum financial gain.All the case studies presented in the paper show how the optimum ESS capacity is determined for peak demand reductions on a particular site.The proposed battery model considers the instantaneous nature of the discharging current and battery temperature.By incorporating these factors into the battery model,a more accurate mode of the battery degradation in real-world scenarios can be achieved.Several key findings are drawn from the case studies.The importance of considering the instantaneous changes in the discharging current and battery temperature over time is shown.The results from these case studies show that there is a significant difference in the resulted degradation when the instantaneous discharging current and battery temperature are used instead of the constant ones.In addition,the battery model is shown to be robust against calibration errors as shown in the sensitivity analysis.
The life-cycle assessment is used to determine the optimal ESS capacity for peak demand reductions of a university building.The ESS capacity ranging from 27 kWh to 917 kWh is considered.The operation strategy of ESS is designed to provide the maximum savings in the peak demand charges while also maximizing its lifespan.The peak demand savings are calculated based on the electrical tariff in Malaysia.The ESS lifespan is calculated by using the battery model.Based on the results,381-kWh ESS can provide the maximum net savings of 250313 MYR over its operational lifespan of 13.2 years.
The findings of this paper have important implications for the design and operation of ESS in peak demand reduction applications.By using the life-cycle assessment,battery operation strategies can be optimized to minimize the degradation and maximize the battery lifespan while also achieving the maximum peak demand reductions,therefore providing additional financial incentives for more consumers to consider the use of ESS for peak demand reductions.The battery model has not been used for other grid services such as frequency control,voltage mitigation,and net zero carbon emissions.There will be different challenges and requirements when the model is used for different grid services.The ESS capacity evaluation is important in the financial feasibility study and should be aided with the proposed battery model as it can consider the different charging and discharging scenarios to determine the degradation accurately.Such an evaluation should be a common or standard practice in the future.
Acknowledgement
The authors would like to gratefully acknowledge the financial support from PETRONAS.
Declaration of competing interest
The authors declare no conflicts of interest.
 Journal of Electronic Science and Technology2023年4期
Journal of Electronic Science and Technology2023年4期
- Journal of Electronic Science and Technology的其它文章
- Developing microwave-induced thermoacoustic tomography: System,application,and reconstruction
- Low working loss Si/4H-SiC heterojunction MOSFET with analysis of the gate-controlled tunneling effect
- High-sensitivity phase imaging eddy current magneto-optical system for carbon fiber reinforced polymers detection
- Algorithms for automatic measurement of SIS-type hysteretic underdamped Josephson junction’s parameters by current-voltage characteristics
- Boundedness and liveness enforcement for labeled Petri nets using transition priority
- Characteristics of sub-synchronous oscillation in grid-connected wind farm system
