基于高斯Copula贝叶斯模型的盾构下穿既有隧道施工风险的分析

吴忠坦

(武汉地铁集团有限公司, 武汉 430030)

如何有效评估和控制盾构下穿既有隧道施工安全风险,降低事故发生概率,是隧道工程亟待解决的问题。外部地质环境和内部隧道结构是动态变化的,盾构施工安全致险因素间也存在一定的相关性,增加了风险分析的不确定性。目前,国内外对于盾构下穿既有隧道的施工安全研究主要集中于既有隧道的变形预测,一般采用理论公式法、数值模拟法和模型试验法。Zhang等提出求解新建隧道下穿施工下既有隧道变形响应的解析方法,模拟新隧道开挖引起既有隧道的地面扰动。[1]陶宇等以在建地铁隧道下穿既有隧道为研究对象,对盾构下穿既有车行隧道施工引起的结构变形及地层土体变形影响情况进行综合分析并提出新建盾构隧道合理的掘进方案。[2]Yin等采用有限元分析软件ABAQUS模拟了盾构下穿既有隧道施工过程,考虑土压平衡盾构开挖间隙对既有隧道沉降的影响。[3]黄向阳等基于Midas GTS构建精细化的盾构下穿既有隧道施工的模型,分析了盾构下穿既有隧道施工中隧道的应力和变形,评估了上软下硬地层中盾构下穿既有隧道施工过程中既有隧道的响应和安全。[4]Ma等进行了一系列三维离心机模型试验,研究不同深度的并列双隧道对干砂中既有埋藏管道的影响。[5]阿卜杜拉等通过盾构隧道的挖掘模型试验,针对既有隧道的应力变化,研究了盾构下穿对既有隧道施工的影响。[6]上述研究侧重于既有隧道变形响应,缺乏从施工系统的角度进行安全风险分析。而隧道外部环境和内部结构不断动态变化,均会给风险分析带来不确定性。[7]传统的云模型、事故树、层次分析法等风险评价分析手段,不能很好地考虑因素关联性,且模型不能动态更新,不利于管理人员实时决策。因此,建模时须考虑各种风险指标的耦合关系,实现基于实测数据的风险评估结果的实时更新,进而合理控制盾构下穿既有隧道施工过程中的风险。[8]

考虑到影响盾构下穿施工风险的因素较多,且各因素之间存在耦合作用,因此,将贝叶斯网络的动态推理诊断与Copula理论的依赖性表达相结合,在不确定和不完全信息下构建了盾构下穿既有隧道施工风险分析的高斯Copula贝叶斯网络(GCBN)模型。通过高斯Copula学习确定潜在风险因素的最佳拟合边际分布,在确定贝叶斯网络的结点和相关性后,建立GCBN模型,识别施工安全风险状态,并从定性和定量两方面推理分析各因素的敏感性,确定较为敏感的风险因素作为重点关注对象,为盾构隧道下穿既有隧道施工风险分析提供决策支持。

1 方法及原理

1.1 高斯Copula理论

Copula理论可以解决多维参数之间构建联合分布函数的问题,变量间边际分布函数的选择与Copula函数的选择互不干扰,可以分别进行,灵活性很高。即使在很大的统计不确定性下,高斯Copula也很容易构建依赖关系,是唯一可以用不完全数据模拟二元分布的Copula函数。[9]高斯Copula分布函数[10]如式 (1)所示:

CGaussian(u1,u2,…,un;θ)=Φn(Φ-1(u1),Φ-1(u2),…,Φ-1(un);θ)

(1)

式中:θ为对角线上所有元素为1的n阶对称正定矩阵,表示copula函数的相关参数;Φn(Φ-1(u1),Φ-1(u2),…,Φ-1(un);θ)为一个n维标准正态分布函数,其相关系数矩阵为θ;Φ-1为一维正态分布函数Φ的反函数,高斯Copula的概率密度函数如式 (2)所示:

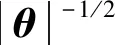
(2)

其中ζ′=Φ-1(u1),Φ-1(u2),…,Φ-1(un)

式中:|θ|为矩阵θ的行列式值;ζ′为标准正态分布变量;I为一个n阶单位矩阵;n阶对称矩阵θ的相关参数θij∈[-1,1](i=1,2,…,n-1;j=2,3,…,n),参数的绝对值越接近1,说明参数之间的相关性越强;参数的绝对值越接近0,说明参数之间的相关性越弱。

1.2 贝叶斯网络

基于有向无环图,贝叶斯网络描述了变量之间的概率关系,概率用于解决变量之间的条件相关性引起的不确定性,而不确定性知识和信息可以被推理。一个贝叶斯网络可以表示为:

BN=〈X,E,P〉

(3)

其中X={x1,x2,…,xn}
E={a11,…aij,…,ann}

式中:〈X,E〉为贝叶斯网络结构的二进制矩阵;X为贝叶斯网络中每结点变量的矩阵;E为贝叶斯网络中结点xi与结点xj间关系的矩阵[11];P为贝叶斯网络中每个结点xi∈X的条件概率,可以定量描述每个结点之间的依赖关系,记为P(xi|Pa(xi));Pa(xi)为网络结构〈X,E〉中的父结点xi的集合,贝叶斯网络中结点间的联合概率分布,如式 (4)[12]所示:

(4)

2 基于GCBN盾构施工安全风险分析方法

考虑到盾构下穿既有隧道施工安全风险因素的复杂性和依赖性建模的难度,很难对施工风险进行全面有效的分析,因此,将高斯Copula集成到贝叶斯网络中,不仅可以实现基于贝叶斯网络结点因子间的实时推理,还可基于高斯Copula挖掘现有数据集中变量间的依赖关系。基于GCBN模型的盾构施工安全风险分析过程,包括三个主要步骤:1)高斯Copula学习;2)贝叶斯网络拓扑构建;3)推理分析。

2.1 高斯Copula学习

2.1.1边际分布识别

根据测量数据选择指标的边际分布是使风险评估过程动态和连续的重要步骤。因此,选取正态分布函数、对数正态分布函数和Gamma分布函数作为候选函数,选择最符合实测数据分布趋势的函数作为最优函数。Akaike信息准则(AIC)实现简单,在识别效果最佳的函数方面表现良好,在当前研究中得到了广泛应用。AIC可通过式 (5)[13]计算,最佳边际分布对应AIC值最小的分布函数类别,[14]考虑到并非所有风险指标都服从相同的边际分布,因此须分别计算各个指标的AIC值。

αΑΙC=-2lnL+2n

(5)

式中:L为模型的极大似然函数;n为参数维度,由于文中每一个风险指标对应一个最优分布函数,n值取为1。

2.1.2模型验证

为验证每个指标所选边际分布的有效性,进行Kolmogorov-Smirnov (K-S)拟合优度检验,衡量估计的边际分布与经验分布函数之间的距离,可通过式 (6)[15]计算:

Dn=max|Fexp(x)-Fobs|

(6)

式中:Fexp为原假设中的累积分布函数;Fobs为经验分布函数。

假设检验的目的是判断一组样本是否服从某个概率分布,或者比较两组样本的分布是否相同,对于选定的显著性水平,如果Dn值等于或大于临界值,则拒绝原假设。

2.2 贝叶斯网络拓扑构建

2.2.1网络结点识别

构建贝叶斯网络模型首先须识别网络中的结点,表征网络中的系统变量。网络中结点按影响方向可分为根结点、中间结点和叶结点。根结点是顶端结点,表示事故的直接致因;中间结点连接根结点和叶结点,表示事故引发的响应;叶结点是末端结点,表示事故造成的状态或结果。[16]

2.2.2网络结构开发

网络结构的构建依赖于变量结点间的因果关系。在传统的贝叶斯网络中,事故风险因素被视为网络结点,用有向箭头连接各个结点,以表征事件中变量间的相关性。为此,开发了GCBN网络模型,将相关系数添加到结点的方向箭头以量化相关关系,相关系数越大,相关性越显著。结合工程经验和专家知识,将事故系统中的风险因素作为贝叶斯网络结点输入模型。根据风险因素的实测数据,对构建的网络模型中的结点进行基于Pearson相关系数的独立假设检验,进而确定最终适合事故原因分析的GCBN模型的贝叶斯网络结构。Pearson相关系数γx1,x2衡量两个变量x1与x2之间的线性关系的强度,通过式 (7)[17]计算获得:

(7)

式中:μx1、μx2分别为x1、x2的均值;σx1、σx2分别为x1、x2的标准差。

2.3 推理分析

为验证所开发的GCBN模型的准确性,将模型输出结果与实际盾构下穿施工安全风险状态进行对比,通过相关分析可以找出对施工安全敏感的关键风险因素,实现对盾构下穿施工安全风险动态和全面的评估。

2.3.1盾构下穿施工安全风险评估

通过构建GCBN风险决策分析模型,将施工安全风险视作动态、连续过程,针对工程项目划分风险等级后,将风险因素实测数据输入GCBN模型,输出条件下隧道漏水风险值的分布。根据模型计算出的施工安全风险平均值和最大值与风险等级区间的对应关系,确定GCBN模型输出的盾构下穿施工安全风险等级状态。通过将GCBN模型输出的施工安全风险状态与实际风险状态进行对比,判断该模型是否能够很好地捕捉施工风险系统的结构关系,从而对施工风险状态进行准确分类,为事故防控提供科学决策支持。

在已知联合概率分布的情况下,通过网络模型推理,可以计算根结点下m个致险因素Vi(i=1,2,…,m)共同作用后叶结点下施工安全风险OC的概率区间,如式 (8)所示:

P(OC=t)=P(OC=t|V1=v1,V2=v2,…,Vn=vn)P(V1=v1,V2=v2,…,Vn=vn)

(8)

式中:P(OC=t)为施工安全对应风险等级t下的概率;Vi=vi为根结点Vi对应的风险等级状态为vi,P(OC=t|V1=v1,V2=v2,…,Vn=vn)为叶结点下施工安全风险OC的条件概率分布,P(V1=v1,V2=v2,…,Vn=vn)为根结点下致险因素Vi组合的联合概率分布。

2.3.2相关性分析

相关性分析主要是根据风险系统中指标的相关程度来确定决策的优先级。高斯Copula可以有效获取参数间相关关系,相关性较大的风险指标是管控的关键指标,具有优先决策顺序。采用蛛网图定性分析风险指标之间的相关性,[18]可视化展示施工安全致险因素的分布,横坐标为系统中的风险指标Vi,纵坐标为对[0,1]区间的划分,反映了各指标取值占比,单一样本全部风险指标取值组合构成了模型中一条折线。进一步地,可以对蛛网图进行条件化处理,通过设定某一因素取值区间观察其余因素受该因素影响后取值变化情况,有助于挖掘施工安全系统中敏感性风险因素。

相关系数可定量分析变量之间的相关程度。[19]通过计算各致险因素与施工安全风险值间相关系数可以确定有较大概率导致风险事件发生的关键指标。对于风险系统中的线性相关,选择Pearson系数来确定每个风险指标(Vi)和风险值(OC)是否线性相关,衡量这种关系正负情况,并确定显著程度。计算式如式 (9)[20]所示:

(9)

对于风险系统中的非线性相关,选择Spearman系数来判断每个风险指标(Vi)与风险值(OC)之间是否存在非线性相关,并衡量显著程度。

3 案例分析

以武汉轨道交通12号线茶叶所站—青菱站区间下穿既有7号线湖工大站—板桥站区间隧道为研究对象。新建12号线区间纵断面线路出茶叶所站后到达青菱站,结构覆土厚度为10.5～32 m,区间场地为长江二—一级阶地。既有7号线湖工大站—板桥站区间线路右线长为843.024 m,左线长为842.388 m,隧道顶覆土厚为15.1～21.3 m。考虑到下穿段发生施工风险事故概率较高,选择12号线左线下穿施工区间段作为研究对象,具体从CK33+850—CK33+950,综合考虑施工参数、地质参数和几何参数,实现隧道掘进施工过程中的安全风险实时分析和控制。

3.1 盾构施工安全风险指标体系的构建

1)隧道相关参数:既有隧道健康情况(V1)一定程度上决定了隧道承受变形的能力,[21]对施工安全风险控制有重要影响。新建隧道相关参数的设计对盾构隧道周围土体和结构有重要影响,可以反映隧道开挖的总体情况。新建隧道直径将直接影响新建隧道对周围土体的扰动,对既有隧道的变形产生影响。[22]考虑到对于一个特定的隧道工程项目,隧道直径是确定的,故研究不作为分析指标。此外,两隧道净距(V2)和两隧道夹角(V3)对盾构施工过程中既有隧道正常运营有重要影响。[23]

2)地质参数:作为一种中间介质,土体条件对盾构下穿施工造成既有隧道产生变形的影响重大。不同的土质会产生不同的扰动,导致既有隧道不同程度的变形。[24]其中,压缩模量(V4)、黏聚力(V5)、内摩擦角(V6)和孔隙比(V7)是表征土体性质的几个常见影响因素。

3)盾构施工参数:在新建隧道施工阶段,合理控制盾构施工参数对于既有隧道运营管理非常有帮助,具体选择了土仓压力(V8)、总推力(V9)、掘进速度(V10)、刀盘扭矩(V11)和注浆压力(V12)5个主要施工参数,考虑到盾构施工过程的复杂性和环境的敏感性,须根据实际情况选择合适的施工参数范围。

为评估12号线隧道下穿既有7号线施工阶段安全风险,更好地进行风险管理,在该区段内共设置了100个监测点,获取相关监测数据如表1所示。

表1 盾构下穿施工区段监测数据

表2 施工安全风险等级划分标准

选取基于盾构下穿施工相关项目研究和不同单位同一梯队的专家的经验知识获取的12个确定的变量作为评价指标,衡量变量对案例施工安全风险的影响。综合考虑以往盾构隧道工程中专家意见和与施工安全风险相关的知识库,将施工安全风险等级映射到[0,1]区间,依次对应为5个安全状态,各施工安全风险等级与划分区间值的对应关系[8]如表 2所示。

盾构下穿施工安全风险值OC通过专家组决策得到,OC的期望值越大,发生安全事故的风险就越大,因此,须识别安全风险系统中的关键因素,并加强安全管控。

3.2 高斯Copula贝叶斯模型构建

3.2.1风险指标边际分布类型的确定

施工安全风险系统中,不同因素服从的边际分布是不同的。利用式 (5)计算实测数据在不同边际分布下αΑΙC,确定最能表征风险指标实测值分布规律的最优边际分布函数为使得αΑΙC最小的函数。采用K-S检验对计算得到的边际分布的有效性进行验证,设置置信区间α为0.05。

图1给出了12个施工安全风险影响因素的边际分布拟合情况。

a—既有隧道健康对数正态分布概率; b—两隧道净距正态分布概率; c—两隧道夹角伽马分布概率; d—压缩模量正态分布概率; e—黏聚力对数正态分布概率;f—内摩擦角伽马分布概率; g—孔隙比正态分布概率; h—土仓压力伽马分布概率; i—总推力对数正态分布概率; j—掘进速度正态分布概率; k—刀盘扭矩正态分布概率;l—注浆压力伽马分布概率。μ为样本均值;σ为样本标准差;α、β分别为伽马分布的形态参数和尺度参数。

图2 盾构下穿施工安全影响因素的相关性分析

图3 盾构下穿施工安全风险分析GCBN模型

可以发现:不同风险因素的最佳拟合边际分布也不相同。

图 1中:两隧道净距、压缩模量、孔隙比、掘进速度和刀盘扭矩的最优分布类型为正态分布,既有隧道健康情况、黏聚力和总推力的最优分布类型为对数正态分布,两隧道夹角、内摩擦角、土仓压力和注浆压力的最优分布类型为伽马分布。

3.2.2结点间的独立性检验

为了减少对专家知识的依赖,提高所构建贝叶斯网络的可靠性,基于式 (7)Pearson相关系数表达式表征网络中各结点间的连接关系,并绘制热图,如图 2所示。设定显著性水平为0.1,若P值大于显著性水平0.1,则两结点为独立关系,反之,两结点间存在一定程度的相关关系。在图 2中,大于0的Pearson秩相关系数值用红色方形表示,小于0的Pearson秩相关系数值用蓝色方形表示。颜色越深,表示两个变量间相关程度越强。值得注意的是:尽管基于Pearson秩相关系数的热图反映了各施工安全致险因素之间相关性的强弱,但不能确定连接结点间箭头的方向。因此,为构建完整的贝叶斯网络,仍须依赖专家知识和现场检查结果对网络进行完善。

3.2.3GCBN模型开发

结合因素间相关关系和专家知识,可以表达贝叶斯网络中结点连接关系,进而构建盾构施工安全风险分析GCBN模型,如图 3所示。在图 3中,12个潜在致险因素和施工风险值OC被作为GCBN模型中的各结点,结点间的连线表示了因素间复杂的因果关系。图 3将边际分布可视化,并详细显示了各结点的均值和标准差。观察可见:在不同的边际分布下,每个结点的特征存在明显的差异。

3.3 结果分析

3.3.1施工安全风险评估

为验证构建的GCBN模型的可靠性,从在项目区段设置的100个监测点中随机抽选10个监测点,依次编号。输入每个监测点对应的施工安全风险指标归一化后的实测值,GCBN模型会输出对应的施工安全风险值(OC),依据表 2中施工安全风险值与安全状态的对应关系,可确定每个监测点对应的施工安全风险状态,结果如图 4所示。

在图4中,通过虚线将盾构下穿施工安全风险值划分为了5个区间。观察发现:针对施工安全风险值,GCBN模型预测结果与专家评价结果吻合,对应相同的施工安全风险状态,验证了所构建GCBN渗漏水风险分析模型的可靠性。应该注意的是:图 4中10个监测点均有不同程度的施工安全风险,4号和5号监测点的施工安全风险状态为Ⅰ级,即安全状态;剩下的监测点中,4个监测点施工安全风险状态为Ⅱ级,即较安全,分别是1号、2号、6号和10号监测点;3个监测点施工安全风险状态为Ⅲ级,即基本安全,分别是3号、8号和9号监测点;7号监测点施工安全风险状态为4级,即较危险。

图5 条件化百分位蛛网

在图4中,该新建隧道施工安全风险均值计算结果为E(OC)=0.414,对应等级为基本安全。标准差计算结果为σ(OC)=0.321,则隧道的施工安全风险值位于[0.093,0.735]内。考虑到隧道施工安全风险值方差较大,若控制不当,风险等级会处于较危险状态,如图 4中的7号监测点。因此,有必要对隧道施工安全风险指标进一步分析,确定施工安全风险关键影响因素,进而采取措施进行防治。

3.3.2定性分析

蜘蛛网图用于对高维模型联合分布的可视化探索,横坐标代表各风险因素,纵坐标代表各风险因素的取值百分位数[0,100%]。为探究隧道施工安全风险值(OC)与风险因素(Vi)间的关系,分别取OC处于安全[0.00,0.10]和危险[0.75,1.00]两种状态进行研究,如图 5所示。设定样本量为5 000,从左到右的竖直线依次表示隧道施工安全风险值(OC)和12个施工安全风险因素。通过条件化区间,发现当施工安全风险值处于危险(高值)状态时,V1、V2和V3处于低值,集中在蛛网图底部。当施工安全风险值处于安全(低值)状态时,V1、V2和V3处于高值,集中在蛛网图顶部。由此可以说明,既有隧道健康情况(V1)、两隧道净距(V2)和两隧道夹角(V3)的变化与隧道施工安全风险值(OC)是完全相反的,意味着这三个因素更有可能对隧道施工安全风险产生相当大的影响。

为进一步说明因素V1、V2和V3与盾构隧道施工安全风险值OC的相关性,绘制OC-V1、OC-V2和OC-V3散点图,并选择OC-V4作为对比,如图 6所示。横坐标分别反映了因素V1、V2、V3和V4的取值波动范围,纵坐标反映了盾构隧道施工安全风险值OC的对应变化情况。相比于图 6d中散点的随机分布,由图 6a、6b和6c可以发现:OC-V1、OC-V2和OC-V3存在显著的负相关关系,这也验证了图 6中百分位蛛网图的结果。从定性的角度,认识到既有隧道健康情况(V1)、两隧道净距(V2)和两隧道夹角(V3)是影响盾构隧道施工安全风险的关键因素,在隧道施工安全风险控制中须优先进行管理决策。

3.3.3定量分析

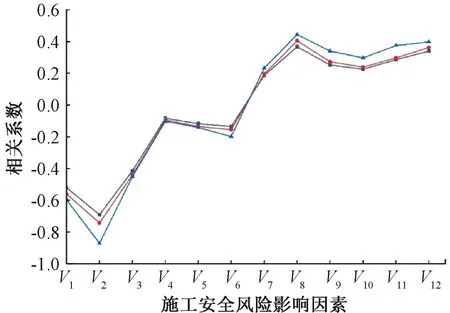
构建的盾构隧道施工安全风险系统GCBN模型中,底层风险指标与施工安全风险间可能存在线性相关关系,故根据式 (7)计算各个底层风险指标关于施工安全风险的Pearson积矩相关来判断系统风险指标的线性相关关系的显著程度,结果如图 7所示。通常,当相关系数的绝对值大于0.5时,认为两个变量相关性较强。在图6可以发现:既有隧道健康情况(V1)和两隧道净距(V2)与盾构隧道施工安全风险值(OC)间Pearson相关系数绝对值最大,均大于0.5,说明这两个因素与盾构隧道施工安全风险呈显著负相关。在线性相关关系下计算底层风险指标与盾构隧道施工安全风险值间的回归系数,进一步判断线性相关关系的大小。构建施工安全风险值为纵坐标y,12个风险因素值为横坐标x的二元一次线性关系式y=ax+b,可以发现:斜率a的绝对值的最大值出现在以两隧道净距(V2)为横坐标的二元一次方程中,为0.873 2。说明在12个风险指标中,两隧道净距(V2)与盾构隧道施工安全风险的线性相关关系最强。

a—OC-V1; b—OC-V2; c—OC-V3; d—OC-V4。

a—防治前 ; b—防治后。

在盾构下穿施工安全风险系统中,底层风险指标与施工安全风险间的相关关系也可能为非线性,此时计算出的Pearson相关系数绝对值会较小,故依据线性相关关系的判断原则,可能判断两者间为

不相关或相关关系较低。故根据式 (9),计算各个底层风险指标关于渗漏水风险的Spearman秩相关系数来判断风险系统中底层风险指标(Vi)与施工安全风险值(OC)的非线性关系的显著程度,结果如图 7所示。可以发现:Spearman秩相关系数中最大的两个值出现在OC-V2和OC-V1中。以V2为例,OC-V2的Spearman相关系数为-0.742 6,则两隧道净距(V2)与施工安全风险(OC)间存在显著非线性负相关关系。同理,既有隧道健康情况(V1)与施工安全风险的非线性关系也呈显著负相关。

3.4 风险防控

研究基于构建的GCBN模型,确定了武汉市轨道交通12号线下穿既有7号线盾构施工过程安全风险等级处于基本安全状态,但某些区段监测点施工安全风险较高,须采取措施进行有效防控和治理。研究确定了隧道施工安全风险的关键影响因素为既有隧道健康情况(V3)和两隧道净距(V4)。考虑到两隧道净距已经确定,无法进行优化调整,为了有针对性地降低隧道施工安全风险,对既有隧道健康情况进行改善。专家认为既有7号线隧道渗漏水情况较严重,综合采取表面封堵法、防水板防水法、喷涂堵漏法、注浆治理法和密封垫防水法进行控制。邀请专家对治理后案例中既有隧道健康情况再次进行打分评价,基于因素V1变化后的结果实现对研究构建的GCBN模型的条件化更新,通过模型中施工安全风险值的变化来反映采取防治措施后隧道施工安全风险优化情况。采取防治措施前、后因素V1数据的变化情况如图 8所示。

在图 8中,经专家评价的既有隧道健康情况得分分布在[45,80]区间内,其中半数以上的监测点健康情况分布在[60,75]区间内,约有1/3的监测点得分低于60,对盾构下穿施工安全控制会产生不利影响。在图 8b中,所有监测点的健康情况得分均达到60以上,其中半数以上的监测点健康情况达到了75分以上。图 8说明了通过采取渗漏水防治措施后,既有隧道健康情况得到了显著提升。

将采取防治措施后由专家评价获取的既有隧道健康情况数据输入构建的GCBN模型进行更新,通过隧道施工安全风险值(OC)的变化情况可以衡量采取的防治措施对隧道施工安全风险的影响,结果如图 9所示。

图 9中,采取控制措施前,既有隧道健康情况(V1)的平均值为63.9,标准差为9.16。对渗漏水进行防治后,既有隧道健康情况(V1)平均值为73.9,标准差为6.98,得到显著改善。通过观察盾构隧道施工安全风险值OC可以发现:在采取预防措施之前,OC的平均值为0.414,标准差为0.321。隧道施工安全风险总体为Ⅲ级,但有向Ⅳ级的趋势,属于高风险状态。采取预防措施后,OC平均值为0.299,标准差为0.248。隧道施工安全风险总体仍为Ⅲ级,但风险值在[0.051,0.547]区间内,相比于原[0.093,0.735]区间,风险状况得到了有效控制。进一步分析表明,开发的GCBN模型条件更新后,隧道施工安全风险值OC的变化主要由既有隧道健康情况(V1)引起。V1结点与OC结点的相关系数为-0.55,为降低盾构下穿工程安全风险作出了较大贡献。

4 结束语

提出了一种混合高斯Copula贝叶斯模型来分析盾构下穿既有隧道施工安全潜在致险因素之间的相互作用。确定了施工安全的关键影响因素,实现了下穿施工过程施工安全风险动态评估。以武汉某隧道下穿既有隧道施工为例,验证了该方法的有效性和实用性。结果表明:

1)基于案例数据得到的隧道施工安全致险因素的边际分布类型不同。考虑正态分布、对数正态分布和Gamma分布三种不同类型分布函数可以更准确地描述不同因素的特征,有助于更合理地开发GCBN风险评估模型。

2)通过蛛网图和散点图进行定性分析,通过相关系数进行定量分析。确定既有隧道健康情况(V1)、两隧道净距(V2)和两隧道夹角(V3)是影响盾构隧道漏水风险值OC的最重要指标。

3)GCBN模型通过更新网络中某些结点的概率,实现对运营隧道漏水风险的实时评估。通过控制既有隧道健康状态(V1)可以实现施工安全风险的合理概率分布,避免事故发生。实例结果表明所提出的GCBN网络模型可以通过动态推理和更新,为运营盾构隧道漏水风险分析提供实时决策支持,从而有效降低复杂系统的风险。