空间关键字top-k查询的why问题
黄金亮,李艳红,卢航
(中南民族大学 计算机科学学院,武汉 430074)
随着移动终端和位置定位技术的飞速发展,越来越多的web 对象具有位置-文本属性,基于地理位置的服务(LBS)逐渐成为了日常所需.在LBS 中,用户可以发起一个查询,检索k个与查询位置最邻近且与查询关键字最相关的兴趣点.虽然LBS 在近些年得到了迅猛的发展,但在查询结果可用性上尚有欠缺.例如,用户想查找周边5 个“咖啡店”,却发现一家“奶茶店”意外地出现在系统返回的查询结果集中(称为why对象),于是对查询结果产生质疑,提出一个why 问题,并且想知道要如何修改自己的查询参数,才能将why对象从查询结果中剔除.若查询系统能对用户提出的why 问题做出合理解释,并向用户提供相对原始查询而言只有微小修改的精炼查询,使why对象被排除在查询结果之外,那将大大提高查询结果的可信度,从而进一步促进LBS 的发展.
传统的空间关键字查询(SKQ)旨在查找与查询关键字最相似、与查询点的位置最邻近的若干个空间文本对象.为了加快SKQ的查询速度,研究者们提出了一系列的查询技术及算法.文献[1]中,用R-tree索引空间对象的位置信息,用倒排文件索引文本信息,但两者并无直接联系,仅是分别通过两种索引查找候选对象,然后将查询结果进行合并.文献[2-3]中,IR-tree 在R-tree 的基础上,为每个结点关联了一个倒排文件,提高了搜索效率.文献[4]提出一种名为IL-Quadtree 的索引结构,该索引结构是由线性四叉树和倒排文件组合构成,为每一个关键字维护一个线性四叉树用于存储包含该关键字的所有对象.此外,文献[5]对不同空间关键字查询索引和查询处理技术进行了综述,为SKQ 的进一步研究提供指导.
查询结果的可用性近几年也成为研究者们关注的热点.文献[6]中指出基于内容意料之外的查询结果分为两种:1)用户想要的对象(why-not)没有出现在结果中;2)用户不想要的对象(why)出现在查询结果中.现有解决why-not问题的方法主要分为三大类,即操作定位、数据库修改和查询修改.这三类方法中,查询修改方法是解决交互性why-not问题的一种绝佳方式.文献[7]使用查询修改来回答top-k偏好查询中的why-not 问题.他们的目的是通过最小限度地修改原始查询使丢失对象出现在结果集中,其中采用了一个度量修改量的惩罚函数.同时,查询修改模型已被应用于回答不同查询和数据设置的why-not 问题,如文献[8-11].最近,文献[12-14]对空间关键字top-k查询的why-not问题进行了研究,这些文献中均使用查询修改来回答空间关键字top-k查询的why-not 问题,分别通过修改用户的偏好、修改查询关键字集以及修改查询方向来回答用户的why-not 问题.文献[15]研究了反向top-k查询中的why-not 与why 问题,其中why 问题部分采用了与解决why-not问题一样的方法,即查询修改.
然而,到目前为止,尚无研究者对空间关键字top-k查询的why 问题展开研究,也没有提出相关研究成果.为此,本文首次定义并研究了空间关键字top-k查询的why 问题.由于能使why 对象被排除在查询结果集之外的精炼查询数量巨大,找出代价最小的精炼查询的时间成本过高.为了加速空间关键字top-k查询的why 问题处理过程,本文设计了一种名为WIR-tree 的混合索引,以在访问一个非叶子结点下的子树前,先估算此结点索引的所有对象与查询之间的空间距离和文本相似性的上限值,进而作相应的剪枝操作.此外,还提出了一个WSKQK 算法,通过编辑距离递增方式枚举候选关键字集,并结合查询处理提早结束策略,加速枚举候选关键字集的整个过程,以达到算法效率提升的目的.
1 问题描述
1.1 空间关键字top-k查询
用D表示空间中的对象集合,任意o∈D都有两个属性(o.loc,o.doc),其中o.loc 和o.doc 分别表示对象的位置和描述对象的文本信息.一个空间关键字top-k查询q=(loc,doc,k,α)包含四个参数,其中,q.loc表示查询位置,q.doc表示查询关键字集,q.k表示检索的对象个数,q.α表示用户的偏好.空间关键字top-k查询根据一个同时考虑空间距离和文本相似度的得分函数检索出k个得分最高的对象.为了提高普适性,本文采用一个较为广泛使用的得分函数[12-14],具体如下:
其中,α表示用户对空间距离和文本相似度的相对偏好.SDist(o,q)表示归一化后的o.loc与q.loc之间的欧式空间距离,可由D中两点之间最大距离对o.loc与q.loc之间的欧式距离进行归一化而获得.TSim(o,q)表示归一化后的o.doc和q.doc的文本相似度,可通过信息检索模型来计算,本文选择Jaccard 相似度模型,具体如下:
其中,|o.doc∩q.doc|表示o.doc与q.doc 交集的关键字个数,|o.doc∪q.doc|表示o.doc 与q.doc 并集的关键字个数.通过上述得分函数计算对象的得分,得分越高的对象其排名越高.对象o的排名具体如下:
定义1空间关键字top-k查询.空间关键字top-k查询返回来自D的k个对象的集合RS,其中,∀o∈RS(∀o′∈D-RS,ST(o,q)≥ST′(o′,q)).
1.2 空间关键字top-k查询的why问题
用户通常很难找到最能描述其查询意图的关键字.因此,确定合适的查询关键字集可以说是发起空间关键字top-k查询的主要挑战.当用户发起一个查询q=(loc,doc0,k0,α)并接收到结果后,可能会发现一个或多个非期望的对象出现在结果集中(称为why 对象).然后,用户提出一组why 对象集W={w1,w2,…,wn},要求系统返回一个精炼查询q′=(loc,doc′,k′,α),以使why 对象被排除在结果集之外.通过对查询关键字集q.doc0和查询对象个数q.k0的修改,可能会产生许多能排除掉why 对象的合格查询.为获得对原始查询修改最小的精炼查询,本文对文献[7,15]采用的代价函数进行微调整,以量化精炼查询相对原始查询的修改量,具体如下:
其中,三个偏好系数β、γ和(1-β-γ)取值范围均为(0,1),分别表示用户对修改q.doc0、修改q.k0和失准度(后续将给出失准度的说明)的偏好.对于精炼查询q′,why 对象的排名q′),查询个数k′=R′(W,q′)-1,k的修改量Δk=|min(0,k′-k0)|,用k0-R(W,q)+1对Δk进行归一化.为简单起见,编辑距离仅考虑插入和删除这两种编辑操作,查询关键字修改量Δdoc 为将doc0转化成doc′所需最小编辑操作数.类似地,用将doc0修改为doc′所需的最大编辑操作数对Δdoc 进行归一化.除此之外,本文将失准度ΔcntN作为结果集对象变化的度量,ΔcntN具体表示精炼查询结果集相对原始查询结果集新加入对象的个数,即ΔcntN=|RS′-RS|,用原始查询的k0对其归一化.
图1给出原始查询q和四个不同对象的位置、文本信息,其中,q.doc0={t1,t2},k0=3,α=0.5.表1列出每个对象归一化后的1-SDist(o,q)值、TSim(o,q)值,以及对象的最终得分ST(o,q).根据这些得分值,why对象w排名第2,它出现在原始结果集中.表2列出了几个精炼查询的详细信息,Δk、Δdoc 和ΔcntN已归一化.由于精炼查询的q′.loc 和3 个偏好系数与原始查询保持不变,表中没有将其列出.本例中,β=0.4,γ=0.3,k0-R(W,q)+1=2,|doc0∪W.doc|=3,由式(4)计算出精炼查询的修改代价,如表2 中Penalty 栏所示,q4的修改代价最小,所以q4为最优的精炼查询.
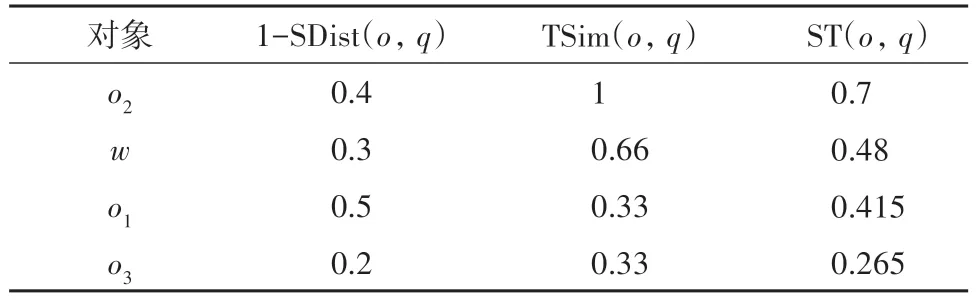
表1 四个空间对象的得分详情Tab.1 Score details of the four spatial objects
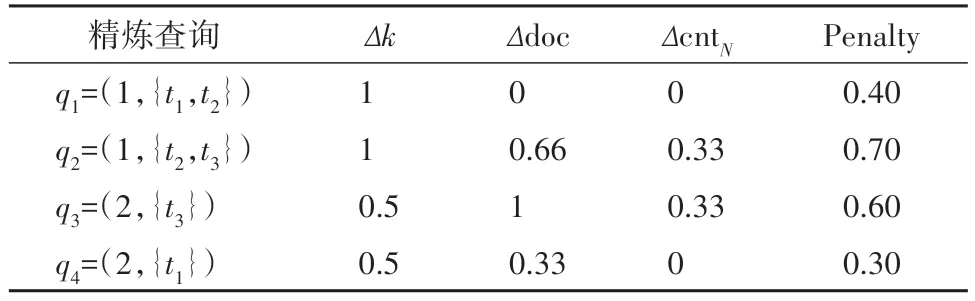
表2 精练查询示例Tab.2 An example of refined query

图1 原始查询及四个空间对象的信息Fig.1 The information of origin query and four spatial objects
定义2空间关键字top-k查询的why 问题.给定原始空间关键字查询q=(loc,doc0,k0,α),原始查询返回的结果集RS,why 对象集W.根据式(4)定义的代价方程,查询系统将返回一个代价最小、且why对象均被排除在结果集RS′之外的精炼查询q′=(loc,doc′,k′,α).
2 WIR-tree索引结构
为了有效地处理空间关键字top-k查询的why问题,本文提出了一种混合索引以同时估算空间距离和文本相似度,该索引结构支持Jaccard 相似模型.这种索引名为WIR-tree,是IR-tree[3]的一种变体.WIR-tree 的叶子结点的结构为(o,mbr,pks),其中,o表示空间中的一个对象,mbr 表示对象的最小边界矩形,pks则表示指向对象o的关键字的指针.WIR-tree的非叶子结点的结构为(pc,mbr,pku,pki),其中,pc表示指向其孩子结点的指针,mbr表示其子树的最小边界矩形,pku 表示指向其索引的所有对象的关键字并集的指针,pki则表示指向其索引的所有对象的关键字交集的指针.图2 为WIR-tree 的示例,非叶子结点R3,它的并集(交集)为R1和R2下所有对象的关键字的并集(交集).
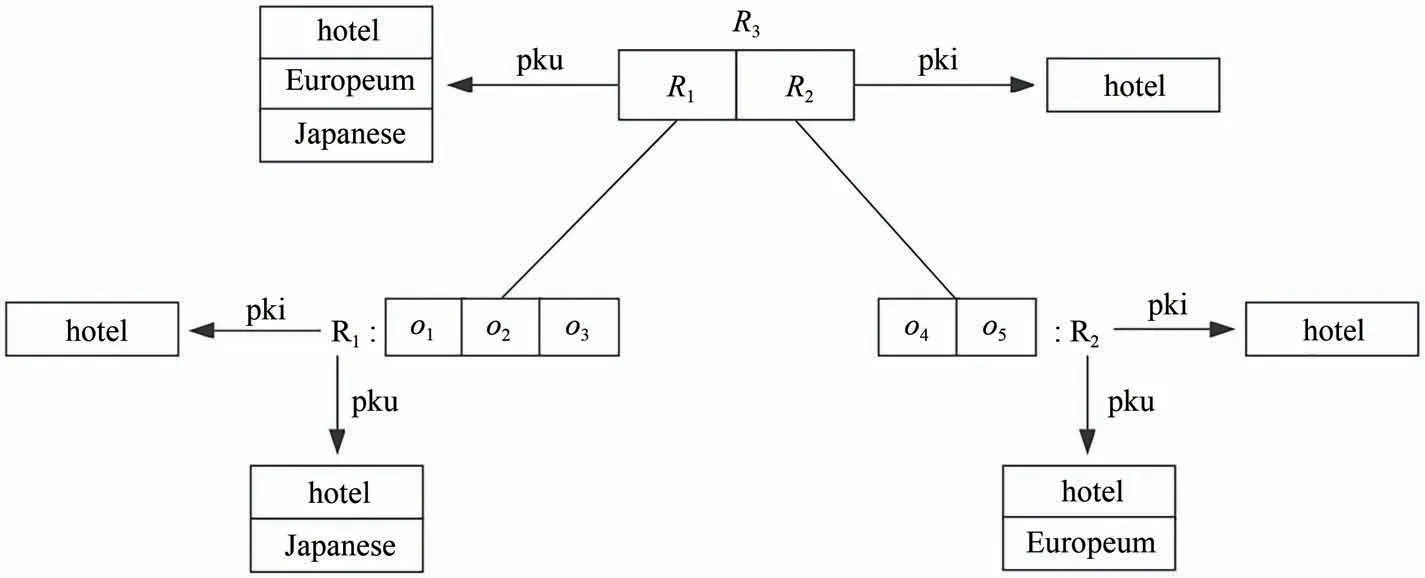
图2 WIR-tree示例Fig.2 An example of WIR-tree
定理1给定查询q=(loc,doc,k,α),WIR-tree中的非叶子结点N,N索引的对象集合S,记MDist(q.loc,N.MBR)为q.loc 和N.MBR 的最小距离,N∪和N∩分别表示结点N下的所有对象的关键字的并集和交集,则下式(5)成立.
证明:由于o被N.MBR 包含,故o.loc 和q.loc 之间的距离一定大于MDist(q.loc,N.MBR),则下式(6)成立,
又因o.doc∈N∪且N∩∈o.doc,得出o.doc∩q.doc∈N∪∩q.doc和N∩∪q.doc ∈o.doc∪q.doc,故下式(7)成立,
结合得分函数ST(o,q)=α·(1-SDist(o,q))+(1-α)TSim(o,q),式(5)中不等式右边的两项都分别大于得分函数中的两项.因此,定理1成立.
定理1 能够利用WIR-tree 来同时估算空间距离和文本相似性的上界,在访问非叶子节点的子树前,先估算其子树下所有空间对象的得分上界,若得分上界小于当前排名为k的对象,则该非叶子结点及其子树可安全地剪枝,这有助于搜索出top-k个最相关的对象.
3 WSKQK算法
基于上述WIR-tree,本文提出了WSKQK 算法,具体思路如下:首先,通过原始查询确定why对象的排名;接着,通过编辑距离递增方式,依次枚举所有可能的查询关键字集;算法执行过程中,始终维护一个当前最优的精炼查询及其修改代价,并结合查询处理提早结束策略,加速枚举候选关键字集的整个过程.最后,返回一个代价最小的精炼查询.
接下来,需要解决的一个重要问题是获取可能的查询关键字集.由于对象集D中不同关键字的总数可能很大,所以可能的查询关键字集个数会很多.因此为每一组关键字执行空间关键字top-k查询是不现实的,为此,提出了以下解决方案.
考虑到添加一个和原始查询结果集不相关的关键字可能会使非why 对象也被排除在结果集之外,同时会加入更多新的结果对象,因此候选关键字只考虑原始查询结果集中存在的关键字.将原始查询结果集中所有对象的关键字划分为3 个子集,即SW、Sc和S!W.其中,SW表示仅why 对象包含而其他结果对象不包含的关键字集合,Sc表示why 对象和其他结果对象均包含的关键字集合,S!W表示why对象不包含而其他结果对象包含的关键字集合.为了在最小程度影响原有结果集的前提下去除why 对象,候选关键字集可以通过将S!W添加到q.doc0或从q.doc0中删除SW、Sc而获得.
3.1 编辑距离递增方式枚举关键字集
候选关键字集的枚举顺序对算法的性能起到关键性作用.候选关键字集的枚举过程中,应该优先考虑更有可能成为最优精炼查询的关键字集,因为对于原始查询关键字集编辑距离越小的精炼查询关键字集,其修改代价越小,因而越有可能成为最优精炼查询的关键字集.首先考虑编辑距离为0的基本精炼查询q′=(q.loc,q.doc′,k′,α),其中基本精炼查询的关键字集与原始查询的关键字集完全相同,即q′.doc′=q.doc,查询个数缩小为q′.k′=R(W,q)-1,由式(4)计算得出基本精炼查询的代价为:
接着根据编辑距离递增的原则,依次枚举编辑距离为n(n=1,2,…,|doc0∪W.doc|)的候选关键字集,具有相同编辑距离的关键字集枚举顺序具体如下:ⅰ)从原始查询关键字集中删除n个关键字,记为dn(Ew=Sw∩q.doc,Ec=Sc∩q.doc,∀dn∈Ew∪Ec);ⅱ)在原始查询关键字集基础上插入n个关键字,记为in(∀in∈S!W).其中,每个候选关键字集将通过执行一个空间关键字top-k查询获得R′(W,q′).最后,由式(4)计算该关键字集对应的精炼查询的修改代价,始终维护当前最优精炼查询最小代价pmin.随着编辑距离n的递增,若出现下式情况:
关键字部分的修改代价已大于pmin,通过代价公式(4)知,剩余的候选关键字集的修改代价绝不会小于pmin,此时,整个候选关键字集枚举过程结束,pmin为最优精练查询的修改代价.
3.2 候选关键字查询处理提早结束策略
对于精炼查询q′(loc,doc′,k′,α),若其为最优精炼查询,由式(4)、(8)得:
上式成立则必须满足Δk′<Δk,即
因此,在执行空间关键字top-k查询过程中,若why 对象的排名不满足式(11),则该候选关键字集的查询处理过程可提早结束,且可安全地排除.若当前查询到的最相关对象个数等于k0时,why 对象还未出现,该关键字集的空间关键字top-k查询处理过程也可提早结束.取k′=k0,此时Δk=0,该关键字集对应的精炼查询代价最小,p′为式(4)的后两项关键字修改代价和失准度之和,即
算法1 为WSKQK 算法的伪代码.ⅰ)首先确定why 对象在原始查询结果集中的排名,使用基本精炼查询初始化最优精炼查询,由式(8)知,此时的pmin为β(第1~2 行);ⅱ)然后,根据候选关键字集枚举顺序,取出下一组关键字ks(第5行),执行空间关键字top-k查询(第10 行),执行过程中每查询到一个top-k对象,判断是否符合提早结束条件(第20~23行);ⅲ)若符合,则结束本轮的空间关键字top-k 查询,否则确定why 对象的排名,进而计算其代价p′,并判断是否更新当前最优精炼查询及pmin(第12-15行).不断从候选关键字集中取出下一组关键字,重复步骤ii)和iii),直至算法结束条件成立,算法结束(第6~7行),返回最优精炼查询(第17行).

4 实验与分析
以基于SetR-tree 索引结构的BS 算法[13]作为对照算法,通过一系列对比实验来验证本文提出的基于WIR-tree索引的WSKQK算法的性能.
4.1 实验设置
4.1.1 实验设备及评估指标
所有实验均在同一台PC 上进行,PC 的配置为Intel Core i7,2.20 GHz CPU 和8 GB 内存.所有算法皆使用Java实现,运行在Windows10操作系统上.本文采用查询时间作为算法性能的评估指标,对每一组实验,随机生成500 个查询取其平均查询时间作为查询时间结果.
4.1.2 数据集
实验选取了EURO和GN两个真实数据集,EURO是一个兴趣点数据集,兴趣点包含ATMs,hotels 和stores.GN 是来自US Board on Geographic Names 提供的公开数据集,包含大量的地理对象.这两个数据集常用于空间关键字的相关研究,它们都包含了许多由一个空间位置和一组关键字表示的对象,更多详情信息见表3.

表3 数据集详情Tab.3 Datasets information
4.1.3 参数
本文通过改变查询的对象个数k0、why 对象的排名R(w,q)、用户对空间距离与文本相似度的偏好α、代价函数的偏好系数(β,γ)及查询关键字个数来评估所提方法的性能.这些参数及其默认值(粗体)如表4所示.
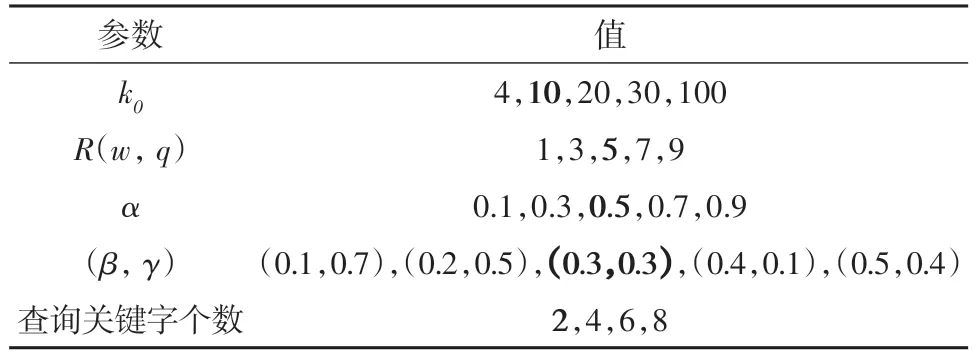
表4 参数设置Tab.4 Parameters setting
4.2 实验结果及分析
(1)k0对算法性能的影响.选取排名为当前k0的一半(即R(o,q)=k0/2)的对象为why 对象,以验证不同的k0取值对算法性能的影响.例如,当原始查询由top-4 变化到top-10 时,相应的why 查询中,why 对象相应为排名第2 的对象和排名第5 的对象.实验结果如图3 所示,由于BS 算法为每一个候选关键字集执行一个空间关键字top-k查询,因此,随k0取值的增长,候选关键字集增大,从而使执行空间关键字top-k查询的时间增大,故BS算法性能对k0的变化非常敏感.然而,WSKQK 算法得益于编辑距离递增方式枚举关键字集和查询处理提早结束策略,它对k0取值的变化敏感降低.如k0=100 时,WSKQK 算法的运行时间约为BS算法的1/3.

图3 k0对算法性能的影响Fig.3 Impact of k0 on algorithm performance
(2)why对象排名对算法性能的影响.由于原始查询为空间关键字top-10 查询,此组实验发起了why 对象的排名分别为1、3、5、7 和9 的5 个why 查询,以验证不同的why 对象排名对算法性能的影响.实验结果如图4 所示,因其候选关键字集的规模并未发生变化,BS 算法的运行时间几乎不受why 对象排名变化的影响.而WSKQK 算法的运行时间随着why 对象的排名增大而减小.具体的原因是,why 对象的排名与k0更接近时,当前最优精炼查询的代价pmin会更小,算法初始的剪枝能力会更强,能够更早地结束查询处理过程.
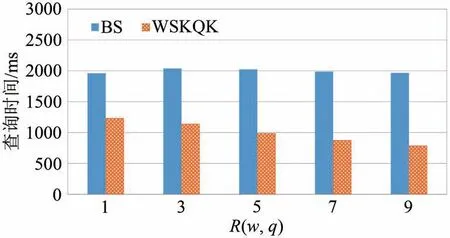
图4 R(w,q)对算法性能的影响Fig.4 Impact of R(w,q)on algorithm performance
(3)α对算法性能的影响.根据空间关键字topk查询的得分公式(1)可知,α越小意味着文本相似性的权重更高,这就降低了空间距离的重要性,因此,基于R-tree及其变体设计的索引,其剪枝能力会降低,可能需要访问更多的树结点以查找到最相关的k个对象.若α越大,则空间近邻度的权重越高,从而降低了文本维度的裁剪能力.实验结果如图5所示,正如以上分析,当α取中间值时,BS和WSKQK算法的运行时间都更短.
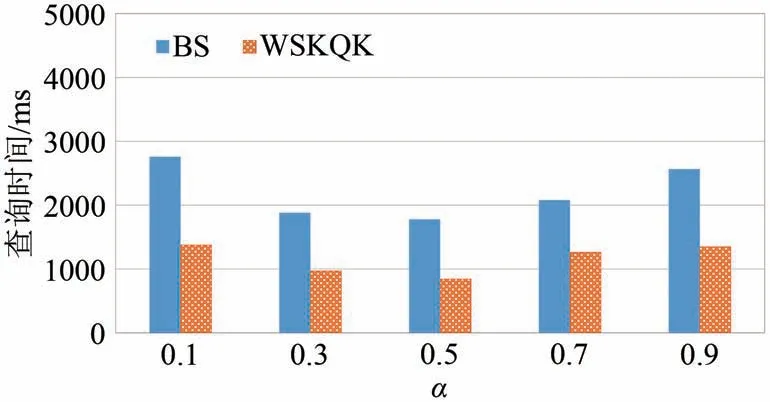
图5 α对算法性能的影响Fig.5 Impact of α on algorithm performance
(4)β和γ对算法性能的影响.这两个参数为用户在修改查询关键字、修改查询个数及失准度这三者之间的偏好.实验结果如图6 所示,由于β和γ只用于在执行空间关键字查询确定why 对象的排名后,计算候选关键字集的代价,所以β和γ对BS算法的性能几乎没有影响.然而,在WSKQK 算法中,使用基本精炼查询初始化最优精炼查询,且始终维护目前最优精炼查询及其代价,以便尽早结束查询处理过程,因而算法性能受β的影响.根据式(6),基本精炼查询的代价为β,较小的β使得初始的pmin较小,这可以提高算法效率,因此,WSKQK 算法的查询时间随着β的增大而增大.

图6 β和γ对算法性能的影响Fig.6 Impact of β and γ on algorithm performance
(5)查询关键字个数对算法性能的影响.关键字的数量会在两个方面影响到算法的性能:ⅰ)查询关键字的增多使候选关键字集的规模增大;ⅱ)关键字数量的增加使计算对象文本与查询关键字的文本相似度所花费的时间有所增加.实验结果如图7所示,候选关键字集规模的增大,使BS 算法的运行时间随关键字数量的增多而显著增加.相比之下,WSKQK 算法的性能随着关键字数量的增多越来越优于BS算法.

图7 查询关键字个数对算法性能的影响Fig.7 Impact of query keyword numbers on algorithm performance
(6)数据集大小对算法性能的影响.为验证算法的可扩展性,本组实验从GN 数据集中随机选择不同数量的空间对象(从0.1 M 到1.7 M),执行空间关键字top-10 查询,以评估不同数据集大小下的算法性能.实验结果如图8 所示,随数据集基数的增加,两种算法的执行时间几乎呈线性增长.具体原因是,这两种算法中候选关键字集的大小不会随着数据集大小的增加而增加.这意味着本文提出的WSKQK算法的性能在不同的数据集下呈平稳趋势.

图8 数据集大小对算法性能的影响Fig.8 Impact of dataset size on algorithm performance
5 结论
本文首次定义并研究了空间关键字top-k查询的why 问题,为用户提供了更能描述他们查询意图的关键字集.设计了一种名为WIR-tree 的索引结构,旨在访问非叶子结点下的子树前完成剪枝操作.基于WIR-tree 索引,提出了WSKQK 算法,通过编辑距离递增方式枚举关键字集,并结合查询处理提早结束策略,来加速整个候选关键字集的枚举过程.最后,采用两个真实数据集,通过WSKQK 与BS 算法的一系列对比实验,验证了所提方法的高效性和可扩展性.未来将探讨不同的文本相似模型及处理多个why对象的情形.

