苏黔两省小学四年级学生数学情境问题解决能力的调查研究

徐时芳,伍国艳

(黔南民族师范学院数学与统计学院,贵州都匀,558000)

一、问题提出

数学情境问题是把数学问题嵌入一个情境之中,包括现实生活情境、其他学科情境。传统的应用题、数学建模都属于数学情境问题。目前大多数情境未受到教科书编制和课堂教学的重点关注,多是人造的、虚拟的情境,鲜见与学生真实生活经验紧密联系的情境。《普通高中数学课程标准(2017年版)》和《义务教育数学课程标准(2022年版)》明确把会用数学的眼光观察现实世界,会用数学的思维分析现实世界,会用数学的语言表达现实世界界定为数学核心素养。[1-2]

许多学者就解答情境问题展开了深入研究。Verschaffel等人和Greer对小学生解答真实性问题做了调查,[3-4]刘儒德等人采用Verschaffel等人和Greer的测验题目对北京市两所小学的学生进行了真实性问题测验,结果发现只有约四分之一的小学生在解答问题时考虑了问题情境的真实性[5]。为了深入了解这个问题,Greer选取了由10个主题组成的情境问题,每个主题都包括两个数学问题,一个是标准的算术问题,另外一个是真实性问题。结果发现,只有17%的小学生在解答问题时考虑了真实情况,大多数学生在解决真实情境问题时表现出了一种排除现实世界的知识倾向。[6]Xin等人仿照国外研究,探究了中国小学四、五、六三个年级学生真实性问题的解决能力,研究结果与国外一致,即学生有较强的排除现实世界的知识和不进行现实考虑的倾向。[7]学生忽视在现实世界用知识解决问题,主要由两个教学因素导致。一方面,刻板的、非创造性的标准情境问题,只要直接使用给定的数学公式、一个或多个数字进行算术运算,就可以将问题解决。另一方面,当前教学实践要求学生必须使用确定的、正确的算术运算解决设定的情境问题,未将建模视角作为真正的数学系统解决方式。[8]

国际学生评估项目(programme for international student assessment,PISA)将数学素养的考查以解决现实世界中真实情境问题为指标,其数学素养测验题目都是情境问题。陈敏等人从PISA试题中选取部分题目进行改编,对六年级学生真实情境问题解决能力的现状展开调查。结果发现,不同的情境对学生解决真实情境问题的能力有不同的影响:学生擅长解决背景素材熟悉问题;语境呈现方式虽不是影响解题的主要因素,但特殊文本会影响学生解答问题;语境干扰程度影响学生对数学问题情境的解答;学生解决情境与数学高度融合的问题与学生本身的知识储备不对应。[9]邓海英等人就数学情境问题解决能力对湖南省小学四年级学生开展了调查研究。结果显示,湖南地区小学四年级学生数学情境问题解决能力不足,不存在性别差异,存在地区(城市、农村)差异,学习成绩与知识迁移显著相关。[10]伍国艳等人调查得出贵州地区小学四年级学生数学情境问题解决能力总体不足,除知识理解得分达到及格水平外,另外两个水平得分均未达到及格水平;江苏地区小学四年级学生数学情境问题解决能力总体较好,知识理解、知识迁移得分达到及格水平,知识创新得分接近及格水平。[11]

解答数学问题可以不考虑现实背景,用纯粹数学的方法解答,但这种学习方法放到现实情境中会出现与现实状况不吻合的情形。对真实性问题的探讨,国内学者多是作重复性验证研究,测试工具大多来自国外,而且研究思路较窄,缺少跨区域研究。对于教育水平存在差异的江苏省和贵州省,其学生在解答情境性问题方面是否存在差异,是一个值得研究的问题,追究其原因对深化教育改革有参照意义。

二、研究方法

(一)被试选择

本研究随机选取贵州江苏两省城市与农村样本共2030名。其中,贵州地区样本数859,占总样本的42.3%;江苏地区样本数1171,占总样本的57.7%。贵州地区样本包含317名农村样本(占总样本的15.6%)和542名城市样本(占总样本的26.7%),分别来自贵州省G县1所乡镇小学2个班;H县1所乡村小学1个班,1所中心完全小学2个班,1所乡镇小学2个班;J县1所中心完全小学2个班;K市1所学校2个班;L市2所学校4个班;M市2所学校6个班,共计农村5所小学9个班,城市5所小学12个班。江苏地区样本包含586名农村样本(占总样本的28.9%)和585名城市样本(占总样本的28.8%),分别来自江苏省N市某实验小学5个班;O市某实验小学3个班;P市某实验小学8个班;Q市1所小学3个班;R市1所小学4个班,共计农村3所小学13个班,城市3所小学16个班。

(二)研究工具

喻平参照布鲁姆模型、PISA模型和可观察学习成果结构模型,将数学知识学习分为知识理解、知识迁移、知识创新三个水平。[12]本研究参照此评价体系,将小学四年级学生数学情境问题解决能力划分为知识理解水平、知识迁移水平、知识创新水平,三种水平能力逐级递增。同时参照喻平“小学四年级学生数学情境问题解决能力测试卷”[10]对小学四年级学生的数学情境问题解决能力进行测试。测试卷中,知识理解水平4道题、知识迁移水平7道题、知识创新水平2道题,试卷满分100分,各水平所占分数比例为28∶41∶31。本研究将小学四年级学生数学情境问题解决能力视为“小学四年级学生数学情境问题解决能力测试卷”得分,在数据处理时,按照惯例将得到该水平总分值的60%视为及格。在2030名被试中随机选取300名被试,经检验,该测试卷的信效度能够进行下一步分析。

三、结果与讨论

本研究基于两省的测试结果,探究两省整体差异、两省在各水平上的差异、两省不同地区的差异、两省学生同一题目得分的差异。

(一)总体情况差异分析

将收集到的贵州省、江苏省学生数学情境问题解决能力测试结果,按学生所在省份进行分组,检验两省学生数学情境问题解决能力的整体差异,结果如表1所示。

表1 两省整体差异

由表1可知,两省的平均值均未达到及格水平,但江苏省平均分更高,且显著高于贵州省。结合教师的教学内容、学生的生活经历和学校资源方面,可能的原因有以下几点。第一,教师在数学领域中的专业素养、在教学过程中对数学知识内容缘由及生成的思考、联系实际生活补充数学知识背景的能力、创新意识及能力等方面都是培养学生数学情境问题解决能力的关键因素。[13]经了解,贵州省农村小学数学教师进行再学习、再深造的机会少于江苏省。第二,测试题目本身并未考虑学生本身的生活经历,如在“颜色合成”与“开车上班”等题中涉及的情境,贵州农村地区学生并不熟悉,可能导致学生不能主动发现数学问题、提不出有价值的数学问题等。第三,学校所在省份或城市不同,其经济水平也不同,导致各学校的教学设备、师资力量、教学资源、教师培训等方面存在差异。这些都可能是影响两省学生数学情境问题解决能力的因素。

(二)两省三个水平差异分析

检验两省学生数学情境问题解决能力在知识理解、知识迁移、知识创新三个水平的差异,结果如表2所示。

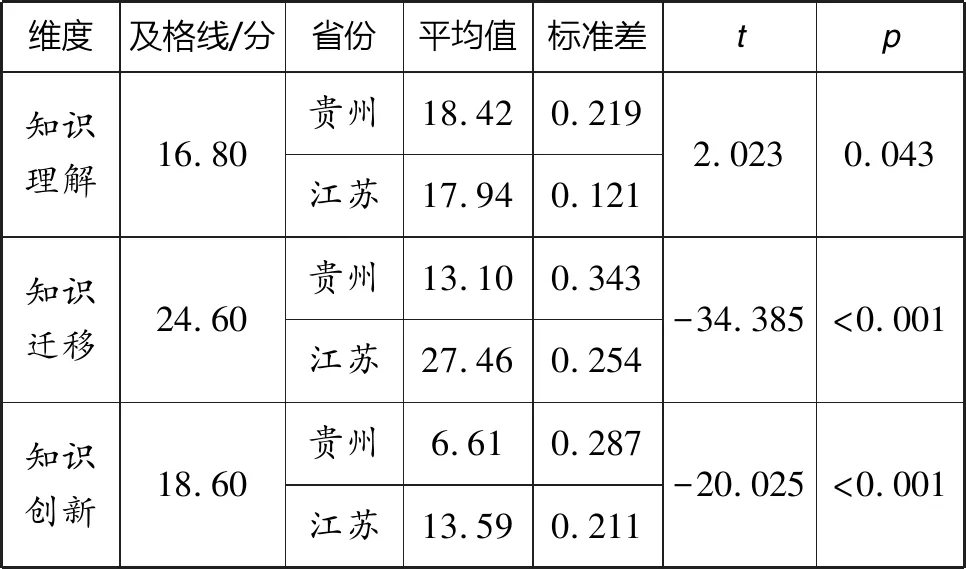
表2 两省三个水平得分差异统计

两省学生知识理解水平分数分别为18.42和17.94,均达到及格线,且贵州省学生得分高于江苏省学生得分,存在显著差异。两省知识迁移水平得分分别为13.10和27.46,江苏省学生达到及格水平,两省存在显著差异。两省被试知识创新水平得分分别为6.61和13.59,均未达到及格水平,且贵州省学生得分显著低于江苏省学生得分。

从上述数据可知,两省被试知识理解能力均达到及格水平,这可能与我国重视“四基教育”(基础知识、基本技能、基本思想、基本活动经验)有关。贵州省学生在数学情境问题解决能力整体水平低于江苏省学生的前提下,其知识理解能力水平显著高于江苏省,可能说明贵州省教师比较重视学生对基础知识的掌握,故学生基础知识夯实,得分较高。另外,测试卷中学生知识理解水平涉及的情境可能更贴近小学生的日常生活,更易于其数学信息的提取,提高了学生解决此类数学问题的正确率。江苏省学生知识迁移与知识创新能力水平得分显著高于贵州省,造成差异的原因可能如下:第一,教师课堂教学的侧重点不同,导致学生数学知识学习的三个水平发展不均衡;第二,不同地区教师的专业素养不同,提出、分析并解决问题的教学策略不同,在日常数学课堂中创设的数学情境类型与取材来源不同,导致两省学生的步伐不一致;第三,部分教师未及时关注教育研究领域的前沿发展,不重视与学校管理者、其他教师、家长、学生的交流。

(三)两省不同地区差异分析

分别检验两省的农村与城市地区学生知识理解、知识迁移、知识创新和数学情境问题解决能力总体的差异,结果如表3所示。

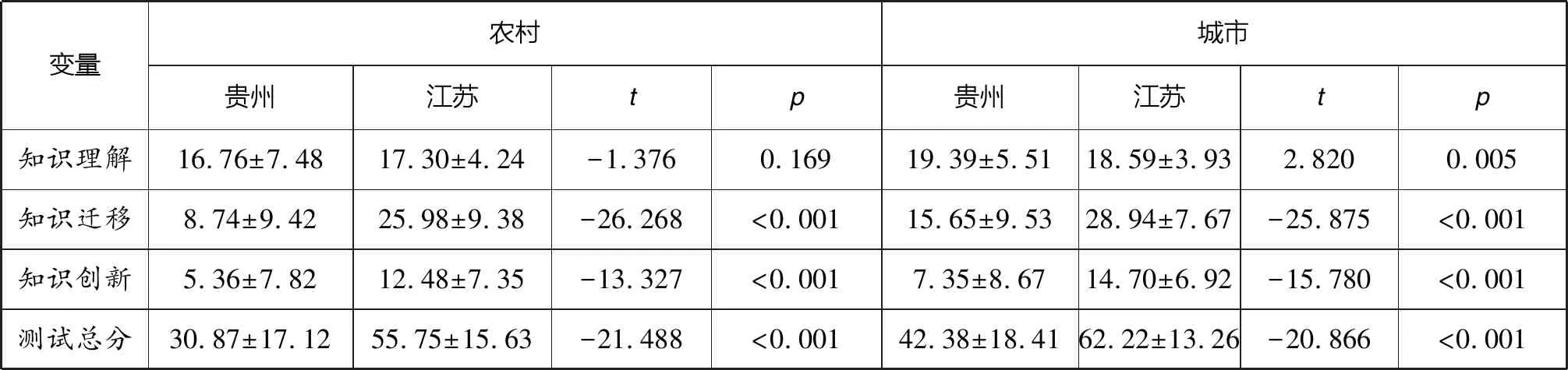
表3 两省不同地区学生均值差异(M±SD)

在农村学生中,两省学生的知识理解水平不存在显著差异,但在知识迁移水平、知识创新水平、数学情境问题解决能力总体上存在显著差异。城市学生中,两省学生数学情境问题解决能力及三种水平都存在显著差异。

从数据上看,不论是在农村还是在城市,学生的知识理解能力基本上能达到及格水平。但具体到作答结果上,与城市学生相比,农村学生的作答有以下几个特点:第一,不提问题或仅提出简单的问题,提出的具体问题仅限于学过的教材内容;第二,不能切身感受教师情境-问题教学中的情境,不能深入了解教师所设情境;第三,提出问题时表述不清晰,文字表达与交流能力差;第四,从数学情境中观察、提取有用信息并解决问题的能力较弱。由于社会发展和生活的需要,农村学生大多数父母会外出务工,学生则成为留守儿童。有学者对贵州农村部分地区留守儿童的父母的文化程度进行调查,发现其父母的受教育程度大多较低,祖辈的文化程度更是如此。[14]学生各项能力和学习习惯没有得到较好的培养,对学习的兴趣也不高。此外,这类学生的家校合作也无法达成,教学效果也无法最大化展现。

(四)两省同一题目两省结果差异分析

两省在本次测试知识中迁移水平均值相差最大的是第5题、知识创新水平均值相差最大的是第9题,具体分析如下。

测试卷第5题:已知颜色的数组表示形式,根据自己的理解,表示出“标准黄色”和“偏红黄色”。

不考虑最终结果的正误,将学生的作答情况分为三类:第一类,未对本题作答;第二类,结果未以数组的形式呈现;第三类,结果以数组形式呈现。分析其具体回答情况可得出以下结论。第一,未对本题作答的学生占大多数,这类学生的基础可能相对较差。相比于学生日常学习中练习的题干,本题题干的字数更多。学生平时练习的题目多是从简短的题干中提取必要信息进行解题,此时遇到题干较长的题目可能无法集中注意力将题目读完,或者缺乏读题兴趣。第二,结果未以数组形式呈现的学生虽然敢于尝试,写下了自己认为正确的答案,但在日常学习中,这类学生的思维可能比较刻板,认为答案就要以数的形式呈现。尽管题干中已经清晰地说明了颜色的数组表示形式,但是这类学生未准确理解,或者无法跳出固有的思维形式。第三,结果以数组形式呈现的学生的基础在整体中相对较好,能以数组的形式呈现答案,能将知识从已知向未知迁移。结合以上分析,联系两省的做法,结果发现,贵州省与江苏省的学生在本题中存在较大差异的原因在于,贵州省处于第一类和第二类的学生多于江苏省,而给出正确结果的学生在第三类。

测试卷第9题:已知蔡老师上班的概况,请自己设计一个情境,提出数学问题并解决。

此题是开放性问题,目的是让学生联系生活实际和自己已有知识,从数学的角度设计一个数学问题情境,并综合运用已有经验作答。将学生的作答结果分为三类:第一类,未对本题进行作答;第二类,只提出了问题却未作答或根据自己的理解列出了算式,得出了没有意义的作答结果;第三类,设计情境、提出问题并解答。在本研究中,两省学生存在显著差异的原因可能是:第一,贵州省未对本题进行作答学生多于江苏省的学生,设计情境、提出问题并解答的学生少于江苏省的学生;第二,江苏省学生提出并解决问题的能力优于贵州省学生;第三,贵州省学生的表达能力较弱,仅有极少数学生可以提出有价值的问题,大多数学生只能提出一步运算的常规性问题;第四,贵州省学生提出问题时更多考虑的是如何更简便地获得正确答案,并未考虑问题本身是否有价值。

问题提出是创新思维的着力点,能够激发学生的创造性思维。[15]张莎莎等人对参加了重庆小学数学“问题提出”教学工作坊教师的教学过程进行研究,发现大部分教师在问题提出教学中设置的任务情境大多是基于教科书内容,围绕教学目标展开,在教学中大多明确且细致地引导学生提问,导致学生自主提问的机会较少。[16]这种引导方式虽然能够避免学生出现大错误,但也限制了学生思维的发散,导致面对开放题时,学生常常会由于缺少教师的步步引导而无从下手。

四、思考及建议

(一)思考

在本研究中,就贵州省和江苏省的教育现状来说,贵州省学生数学情境问题解决能力总体得分与江苏省学生相差过多,值得深思。

第一,按贵州省学生在知识理解水平的表现,推测贵州省学生在知识迁移与知识创新水平得分应与江苏省学生不相上下,甚至更好,但实际比较具体结果则相反:贵州省学生在知识迁移和知识创新方面的得分只有江苏省学生的一半甚至更低。贵州省教师应该思考,在日常教学中,是否只重视学生对基础知识的掌握,并未注重发展学生的其他能力。

第二,从江苏省学生在知识迁移和知识创新水平上的表现来看,其知识理解水平也应高于贵州省学生。但是实际上,城市中江苏省学生知识理解得分低于贵州省学生。江苏省教师应该注意,这可能是因为在日常练习时,没有强调基础知识的重要性,没有培养学生认真审题的习惯,导致学生在测试时忽视了基础知识的重要性,存在不认真读题等情况。

第三,教师需要思考在保证学生知识理解能力充分发展的前提下,均衡发展学生的知识迁移、知识创新能力,以培养学生将同一个知识点迁移运用到另外相似的题型中的能力,更要引导学生对题型进行归纳总结,设计出具有自己思维特点的新题型。

第四,教师要注意提升自己的专业素养,提升自己的教学设计能力,合理地设计出生动有趣、学生愿意参与的“问题提出”课堂。同时,教师也需要思考如何基于学生提出的问题进行合理评价,并能根据问题层层深入,以培养学生的发散思维。教师更要思考如何充分实现家校合作,使家长能够主动、及时地与教师沟通,使家长理解沟通的内容及必要性。

(二)建议

根据本次研究学生在数学情境问题解决上存在的问题,提出以下教学建议。

第一,基于情境,及时评价,伺机教学。提出一个问题往往比解决一个问题更重要。对问题提出的教学,教师可以创设开放式任务情境。这种开放式任务情境不仅能够有效减弱任务背景对学生思维的束缚,更有利于培养学生的创造性思维。教师要将学生提出的、有价值的问题作为数学情境,并及时给予评价,尽量避免使用否定、打击学生学习积极性的评价,在一次次训练中强化学生提出问题的意识与能力。此外,教师还需要精心选择学生提出的问题并进行重点讲解,在讲解问题时重视对学生解题思维的训练。在整个学习过程中,教师不仅要肯定学生在学习中的成功,更要引导学生正视出现的错误,带领学生找到关键因素,分析原因。[17]

第二,开展综合实践活动,积累丰富情境素材。综合实践活动同样需要设置一定的考查内容,不可流于形式。综合实践活动对学生来说是一个积累情境素材的重要过程,能够为教师创设问题情境教学打下更坚实的基础。教师需要针对问题开展实践活动,在丰富学生活动的同时,也能使教学内容更加生活化。将学生生活与数学世界有机融合在一起,将问题融入现实世界的情境,有利于培养学生对数学情境的兴趣,提高学生的学习兴趣。

第三,学科融合,实现情境多样化。数学作为一门基础学科,与其他学科关系密切。依照PISA测评对情境的分类,涉及其他学科情境的数学问题属于科学情境。《义务教育数学课程标准(2022年版)》课程总目标要求学生能体会数学知识之间、数学与其他学科之间、数学与生活之间的联系,在探索真实情境所蕴含的关系中,发现问题和提出问题,运用数学和其他学科的知识与方法分析、解决问题。[2]教师在日常教学时应重视学科外部和内部知识的融合、交叉,以实现知识的跨学科整合和学生思维的融会贯通。通过学科的交融,可以实现科学情境的多样化,有助于提升学生的综合素质、科学精神。在数学教学中体现多学科思维,这对教师的专业素养提出了更高的要求。

第四,提高教师素养,促进学生数学情境问题解决能力的发展。教师是学生学习活动的主导者,是培养人才的关键,在贯彻教育方针、实现人才培养目标上起着重要作用,因此,要把提高教师群体素质作为提高教育质量、推进素质教育、发展数学学科核心素养的前提。提高教师情境教学能力,除了教师要不断学习,还需要学校创设学习条件。例如,通过校本教研、业务培训、师徒制、E-learning等方式,丰富、提高教师的新理论、新技术和新管理方法。另外,课堂观摩、课例研究、同课异构、小课题研究、行动研究等方式都能促进教师的专业发展,加深教师对数学情境问题解决的理解。学校也可以和地方高校合作,为学校教师创造学习条件。例如,吕传汉等人在进行跨文化数学教育研究时,为了提高贵州民族地区数学教师的专业素质,实行了顶岗实习、离岗培训的策略,最后使学校、地方双方受益。[18]

五、结论

本研究采用“小学四年级学生数学情境问题解决能力测试卷”,对贵州省、江苏省的城市、农村共计2030名小学四年级学生进行了测试,发现:江苏省小学四年级学生数学情境问题解决能力显著高于贵州省学生;两省学生数学情境问题解决能力整体存在显著差异;构成数学情境问题解决能力的三个能力水平存在显著差异。数学教师教学要注重情境教学,跨学科开展综合实践活动,不断提升自己的素养,以提升学生的数学情境问题解决能力。