基于地表数据及产状数据的交切断层建模方法研究

赵义来, Alison Ord, 汤静如, 胡荣国, 杨启军,汪劲草, 王本达

基于地表数据及产状数据的交切断层建模方法研究

赵义来1, 2, 3, Alison Ord3, 汤静如1, 2, 胡荣国1, 2, 杨启军1,汪劲草1, 王本达4

(1. 桂林理工大学 地球科学学院, 广西隐伏金属矿产勘查重点实验室, 广西 桂林 541004; 2. 桂林理工大学, 有色金属矿产勘查与资源高效利用协同创新中心, 广西 桂林 541004; 3. Centre for ExplorationTargeting, School of Earth Sciences, University of Western Australia, Perth, WA 6009, Australia; 4. 中国有色集团(广西)平桂飞碟股份有限公司, 广西 贺州 542800)

三维地质建模是地质研究的有力工具, 断层的三维建模比其他地质体建模具有更大的难度, 其中一个主要难题是交切断层切割关系的处理。本文以广西珊瑚矿田为例, 探讨了基于地表数据和产状数据的交切断层建模方法, 采用地表断层线‒剖面断层轨迹‒系列断层线‒断层面的技术路线进行切割断层建模, 采用初始断层面‒断后约束条件‒交切处理‒约束插值的技术路线进行被切割断层的建模, 并与其他建模方法的建模效果进行对比和讨论。最终形成了如下建模方法: ①以旋转法求取部分切割断层的错开部位约束, 以平移法求取完全切割断层的错开部位约束; 以断层错开部位约束、地表断层线约束及断层面边界约束为控制条件, 进行断层面DSI插值, 实现断层错动; ②局部法建模、分段断层线的平移连接及过度追求完全切割关系建模可能分别引起断层面延展可控性差、断面整体偏移误差及沿走向过度延伸问题, 与地质事实相悖, 故本文优选采用了整体法建模、顺延连接分段断层线及遵从原有切割关系的处理方法, 获得了较好的建模效果。

三维地质建模; 交切断层; 部分切割; 约束插值; 珊瑚矿田

0 引 言

三维地质建模是地学研究的有力工具, 所建模型可服务于地质体空间关系分析(Zanchi et al., 2009)、地质属性分析(贾卓等, 2021)、地质过程数值模拟(Zou et al., 2019)等研究。不同的研究具有不同的建模目标: 地质体空间关系分析需要进行几何建模; 地质属性分析和地质过程数值模拟需要进行属性建模。从模型类型来看(吴立新等, 2003): 几何建模多建立曲面模型; 属性建模则需建立网格模型; 网格模型一般是在曲面模型的基础上建立实体模型, 再对实体模型进行剖分得到的。可见, 几何建模在三维地质建模工作中处于基础性地位, 模型质量的好坏不仅会影响后续网格模型质量, 也影响研究结论的可信度。

断层是一类常见的建模对象, 因其切割其他地质体, 控制研究区的构造格架, 而且还记录构造演化信息, 因此, 断层的建模效果对模型质量有重要影响。从断层建模的总体思路来看, 其建模方法可分为整体法和局部法(朱良峰和潘信, 2008)。整体法(Wu et al., 2005; 熊天鹤和袁红旗, 2018)基于对断盘标志层的恢复进行建模, 通过对研究区构造发育历史进行反演, 得出初始未错断的地质模型, 再通过正演计算构造运动造成的地层或断层面的位移或应变, 该建模过程从地质成因视角出发, 所建模型更符合地质过程和地质规律。局部法(Wu and Xu, 2003; 王统等, 2020)是基于分区插值的断层建模技术, 对被错断的地质体分别建模, 最终形成研究区的整体模型, 因该方法进行模型分块处理, 具有较高的灵活性, 但在数据不足的情况下, 各曲面、块体相接部位会出现与地质事实不符的情况, 须在各断层模型完成后及时检查、修正被切割地质体的对应情况。

在建模的具体实现上, 包括人机交互建模和自动化建模两种方式。随着技术和算法的进步, 自动化建模的程度不断提高, 尤其在构造简单区的应用更为广泛, 所采用的算法包括序贯高斯模拟(sequential gaussian simulation)及等值面提取(Cherpeau et al., 2010)、断层表达式法(孙劲光和高天鹏, 2016)、方向包围盒(oriented bounding box, OBB)碰撞检测法(张慧等, 2018)、Hermite径向基函数(HRBF)法和二叉树结构法(邹艳红等, 2020)等。对于构造复杂区, 则需要依据地质知识不断进行判断和干预, 以及时修正建模方向, 确保地质合理性, 因此人机交互建模仍是不可或缺的手段, Duvinage (2000)通过删除及重绘多边形线段, 对建模过程中生成的断层多边形进行人机交互修正, 以避免网络空洞及畸变的产生; Tertois and Mallet (2007)探讨了有新数据加入时断层位置的调整方法, 通过人工拖动断层控制点至更新位置, 再自动计算控制点的变形矢量, 并通过离散光滑插值(DSI)对邻近节点的变形矢量进行调整, 实现模型网格的局部修改; Guo et al. (2018)基于HRBF方法进行断层及地质界面建模, 其中原始数据的输入采用了手动描绘和自动获取两种方式, 提高了对建模过程的监控和地质知识的融入度。

相较于其他地质体建模, 断层建模具有更大的难度, 表现在对部分切割关系的处理, 即两盘标志层的建模。如果标志层被完全错开, 建模难度相对较小, 可用局部法对两盘标志层分别建模, 并将其约束至断层面; 也可采用整体法先对错断前的标志层恢复、建模, 再用断层截切、平移, 实现错动。若标志层被部分切割、错开, 其错开距离由开裂点向断层内部逐渐增大, 不能简单以某个滑距值对两盘进行平移处理, 而应从标志层开裂点到它在断层内的尖灭点进行滑距插值, 从而建立部分切割关系。

断层建模的难度还表现在其深部位置数据和产状数据获取困难, 导致断层的延伸/延深与尖灭情况难以确定。对于这一问题, 有研究者对断层进行简化处理, 方法有三种(Hoffman et al., 2007): ①将断层依趋势延伸/延深至模型边界, 便于处理断层与地层、断层与断层的截切问题; ②对于同倾向断层, 减小断层延深量, 以避免交切; ③对于反倾向断层, 在相交无法避免的情况下, 移动或移走个别断层。也有研究者通过对断层延伸规模、位移量、剖面几何特征、标志层几何特征的研究, 由已知参数推断未知参数, 进行断层建模(Gillespie et al., 1992; Galera et al., 2003; 宋忠航等, 2015; 刘光伟等, 2018)。若将地质模型用于数值模拟, 一种常见的处理方法是在尊重基本地质事实的前提下, 将模型进行适当简化, 以使研究工作聚焦于所关注的地质因素及过程, 并在一定程度上降低建模难度。

针对以上难点, 本文以广西珊瑚矿田为例, 探讨基于地表数据和产状数据的交切断层建模方法, 通过人机交互进行曲面建模, 并对局部法与整体法建模、部分切割关系插值、断层的延伸/延深推断等方面进行了建模试验与讨论, 以期为断层三维地质建模工作提供思路和参考。

1 地质背景

珊瑚矿田位于桂东北富贺钟成矿带中部, 是我国重要的钨锡矿生产基地。矿田内出露地层主要为泥盆系, 是矿区原生钨锡赋矿地层。区内出露岩浆岩为盐田岭花岗岩岩株, 据推测, 长营岭和松宫两处存在隐伏花岗岩体(宋慈安, 2001)。矿田内发育断裂及褶皱构造, 其中断裂是重要的构造类型, 控制该区的构造格架及主要矿化产出。主干断层F1和F3将该区分割为西区EW向褶皱带、中区NE向挤压带和东区SN向褶皱带(图1)。中区发育NE向及NW向断裂, 形成网状构造格局, 控制了矿田主要矿化类型钨锡石英脉型矿体的产出; 西区和东区产出(近)EW向、(近)SN向、NE向和NW向断裂; 矿田内断裂具有多期活动特征并互有切割, 从现今所展现的交切关系来看, 具有(近)EW向/NW向断裂切割NE向断裂, NE向断裂切割(近)SN向断裂的特点。

2 断层特征及复杂性

本文所建曲面模型拟服务于矿田网格建模及成矿过程数值模拟, 因此, 建立成矿模拟起算时刻的模型, 而非现今所见地质模型。珊瑚矿田主成矿作用发生在100.2～102.7 Ma(Li et al., 2015; Zhang et al., 2020), 成矿起算时刻取K1末期, 此时该区受NWW-SEE向拉张应力场控制(韦昌山等, 1993; 舒良树, 2012; Wang and Shu, 2012; Mao et al., 2013; 舒良树等, 2020),出于数值计算边界条件施加的需要, 将模型长轴设为120°方向。

2.1 断层切割层位

下文主要以中区NE向、NW向断层为例进行建模方法探讨。据桂林矿产地质研究院(2008)关于本矿区的地质资料, 区内断层一般切入下泥盆统莲花山组(D1), 西区SN向陡倾断层则切入寒武系。向浅部, NE向、NW向断层主要形成于燕山早期, 至成矿起算时刻, 侏罗系已经沉积, 并被NE向、NW向断层切割, 之后下白垩统(K1)基本完成沉积, 相关文献、资料未显示NE向、NW向断层具有同沉积断层的特征, 故认为其不切割K1。

2.2 断层性质及交切关系

中区断层现今表现的切割关系为NW向断层切割NE向断层, 并呈左行错动, 根据两组断层的产状特征推断, NW向断层总体表现为张性, 即正向错动, 模型中, 须在现今关系的基础上移除喜山期SN向压应力场及燕山晚期NWW-SEE向弧后伸展的影响。喜山期作用下, NW向断层和NE向断层均为压剪性; 燕山晚期, 应力场对NW向断层影响不大(2与断层走向垂直), NE向断层则呈张性, 消除上述两期作用的影响后, 成矿起算时刻, NW向断层仍为张剪性, 而NE向断层很大可能为压剪性(两期构造运动的影响相反, 而度量尚未知), 其性质与现今观察一致, 故沿用这一关系进行成矿起算时刻建模。基于上述分析, 建立该区典型剖面的概念模型(图2)。

3 交切断层三维建模

交切断层建模流程见图3, 包括断层线的编辑与提取、切割断层建模和被切割断层建模3个步骤, 各步骤的详细方法介绍如下。

图3 基于地表数据及产状数据的交切断层建模过程

3.1 断层线的编辑与提取

以地表数据及产状数据作为断层建模数据来源, 地表数据为断层在地表的出露迹线, 产状数据为断层在地表及坑道出露的倾向、倾角, 未获得数据的断层参照同组断层数据进行建模。断层迹线数据见图1, 产状数据见表1。

表1 珊瑚矿田主要断层产状数据

断层线的编辑与提取在AutoCAD中完成。在不影响地层单元划分的前提下, 将同方向的多条断层适当进行删除、简化。NE向断层线被NW向断层错断, 对其进行顺延联结, 恢复至断前状态, 具体做法是: 将两盘断点回缩、相连, 回缩量各取滑距的1/2, 调整断点邻近节点, 使联结后的断层线平滑; NW向断层线未被错断, 直接提取使用。

3.2 切割断层建模

断层线提取后, 建立断层曲面模型, 在GOCAD平台进行曲面建模。GOCAD是一款主要用于油藏、地质、地球物理等领域的三维地质建模软件, 它基于离散光滑插值(DSI)技术, 以工作流程为核心, 可以完成点、线、面、体的全方位建模; 软件采用了对不规则地质体适应能力很强的三角剖分和四面体剖分技术, 尤其适用于建立各种复杂地质体的三维模型。

首先对切割断层建模, 本文所述“切割断层”是指切割其他断层的断层, 即NW向断层。在与断层总体走向垂直的方向建立剖面, 在剖面中, 基于地表断层线及产状数据绘制断层轨迹; 基于前述断层切割层位的推断, 将断层轨迹沿倾向平滑顺延; 在剖面断层轨迹约束下, 将地表断层线复制到不同标高, 得到系列断层线。

将断层线导入到GOCAD软件, 采用断面‒不规则三角网(Section-TIN)法建立断层曲面模型(图4), 该方法以连续平、剖面图上的曲线节点为数据源, 按照一定的插点层数对曲线间的空白区域进行不规则三角面剖分, 从而获得地质体曲面模型(吴立新等, 2003)。曲面三角网尺寸受线上节点间距及线间插点层数控制, 本文主要关注断层的曲面建模及交切处理方法, 故节点间距沿用原始数据, 线间插点层数采用默认设置, 未做调整。在后续基于曲面模型的网格模型建模中, 再对整个模型进行拓扑一致性检验、节点调整(网格尺寸控制)及模型二次重构。

(a) 剖面断层轨迹, 灰色面为地表面, 加粗红线为NW向断层地表迹线; (b) 系列断层线, 为便于观察, 消隐了除NW向断层外的其他地表断层线; (c) 断层曲面模型, 向NW看; (d) 断层曲面模型, 向W看, 为了便于观察, 消隐了其余3条断层。

3.3 被切割断层建模

被切割断层, 即NE向断层, 建模的技术难点在于错动关系的表达, 通过多种方法的对比试验, 本文基于整体法建模思路, 采用建立初始断层面‒求取断后约束条件‒交切处理‒约束插值的技术路线进行建模, 下文以F5断层为例, 进行阐述。

(1) 建立初始断层面。NE向断层建模与NW向断层建模方法类似, 基于地表断层线及前述典型剖面概念模型, 以Section-TIN法建立F5的初始断层面, 此时断层面为完整曲面, 未被NW向断层切割。通过三维场景观察可知, NW向断层对F5的切割关系分为完全切割(F8)和部分切割(F27、F17、F49), 以下将对两种情况分别求取断后约束条件。

(2) 求取断后约束条件。约束条件包括3类: 断层错开部位约束、地表断层线约束及断层面边界约束, 将其用于F5初始断层面插值, 作用在于实现断层面交切错动, 将断层面拟合至原始数据, 以及避免曲面边界畸变的发生。

断层错开部位约束控制断层错动后两盘开裂面的最终位置。对于部分切割关系, 以F5被F17切割为例, 如图5所示, AOB为断层F5的初始剖面轨迹, F5被F17切割, O为开裂点, OB段被错动为OC和OD两部分, C′、D′分别为OC、OD与现今地表的交点。B点的错动过程包含沿F17走向和倾向的位移, 因此断后约束OC和OD的求取可通过断层面F5沿O点(空间上为一直线, 本文取F5过O点的走向线)的旋转来实现。参照地表断层线的错动位置, 将F5分别旋转至过C′及D′点, 求取F5与F17的交线, 得到F5开裂部位的断后约束。对于完全切割关系(被F8切割), 依地表所示错动量(滑距), 将F5初始断层面分别平移至两盘错动后的位置, 并提取其与切割断层(F8)的交线, 即为所求约束(图6)。

图5 断层部分切割关系示意图(观察视角平行于F5走向线)

(a) 俯视图; (b) F5与F8交切关系, F5a和F5b分别为断层F5平移后的曲面位置。观察框水平剖切至地表高度。

由于对NE向断层线进行了断点顺延联结,对其邻近节点进行了位置修改编辑, 断层面在上述位置偏离建模数据, 地表断层线约束的作用是在插值处理中将断层面拟合回原始建模数据, 消除误差。故提取F5的地表分段断层线, 作为约束条件之一。

断层面边界约束的目的是保证曲面插值过程中其边界不发生畸变。沿断层边界施加法向约束, 使边界节点在插值中仅沿断层面法向移动, 以避免面网边界塌陷; 又因初始断层面的边界是基于地表数据延伸推断而来的, 无须将其完全约束, 仅沿法向移动为插值提供了更为灵活的选择, 可避免多维度约束下插值导致的面网拓扑错误。

(3) 交切处理。之所以先提取约束, 再进行交切处理, 是因为交切操作会增加断层开裂部位节点数, 若在此基础上提取约束条件, 将使约束点大量增加, 不仅对控制断层面的错动意义不大, 且易于在插值过程造成拓扑错误。以4条NW向断层对F5进行交切处理, 获得相应开裂面, 每个开裂面为断层面新增两条边界, 边界两两重合, 尚未错动。

(4) 约束插值。将上述约束条件以控制节点的形式施加至断层面, 各约束条件与断层面的关系如图7所示。进行约束下曲面插值, 插值方法选用GOCAD内置的离散光滑插值(DSI)技术, 该技术最早由Mallet (1992)提出, 它是根据约束条件所提供的某些点的目标位置, 在这些点的一定邻域内, 通过解线性方程组求取待插值点的空间位置, 且插值过程中使全局粗糙度和约束违反度具有最小值。因此, 离散光滑插值生成的曲面既能准确地拟合约束, 又能有效地控制网格畸变, 对于地质体建模有很强的适应性。通过插值实现错动, 完成交切断层建模(图8、9)。

图中仅显示一条NW向断层F8, 以示其与F5断层及约束条件的位置关系; 为便于观察, 消隐了断层面三角网, F5曲面设置为半透明。

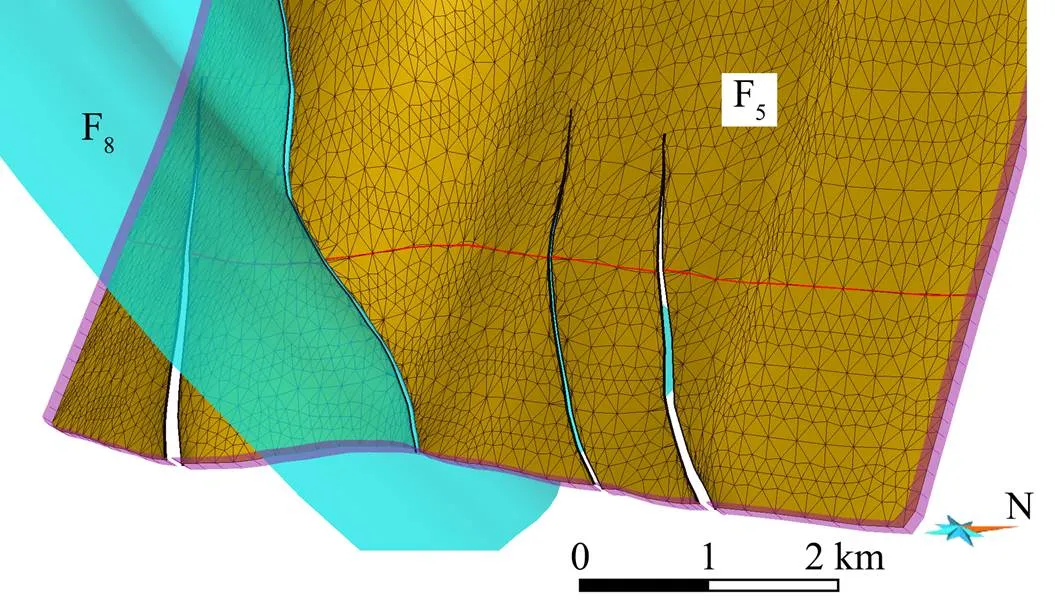
通过插值, 实现了各开裂面的错动; 显示了F5曲面的三角网, 以示约束条件对三角网及节点的控制作用; 图中仅显示一条NW向断层F8, 并设为半透明, 以便于观察; 各约束条件的说明同图7。

(a) 向NE看; (b) 俯视, 建模结果显示了不同方向断层的切割关系, 并完全吻合原始建模数据(地表断层线)。

4 讨 论

除了上述优选建模方法, 本文还尝试使用了其他方法进行建模, 用来对比讨论。

4.1 局部法与整体法建模对比

局部法建模是采用分段建模的思路建立F5各段断层曲面模型, 通过直接提取平面各段断层线, 分别生成其系列剖面线, 以Section-TIN法建立各段断层面, 再以NW断层为边界, 对各段断层面进行延伸或剪切处理, 使之限定在对应的断盘内。

通过试验认为, 该方法在延伸处理环节存在可控性差的问题。因为分段断层面是按照各段的走向趋势进行延伸的, 若断层走向在相邻断盘发生反转, 建模结果无法表达这一特征(图10); 另外, 在剖面上也会引起相邻盘断层面的错动关系与地质事实不甚相符, 如浅部右行错动、深部左行错动(图11)。欲提高断面延展的可控性, 须将相邻盘的断层线设置为约束条件进行插值修正。相比之下, 将各段断层线先行连接, 以整体法建模, 再进行剪切、错动是一个相对高效且符合地质规律的做法。

(a) 局部法建模, 断层沿走向延伸后与相邻断盘数据不甚相符; (b) 整体法建模, 断层面与建模数据吻合度高。观察框水平剖切至地表高度。

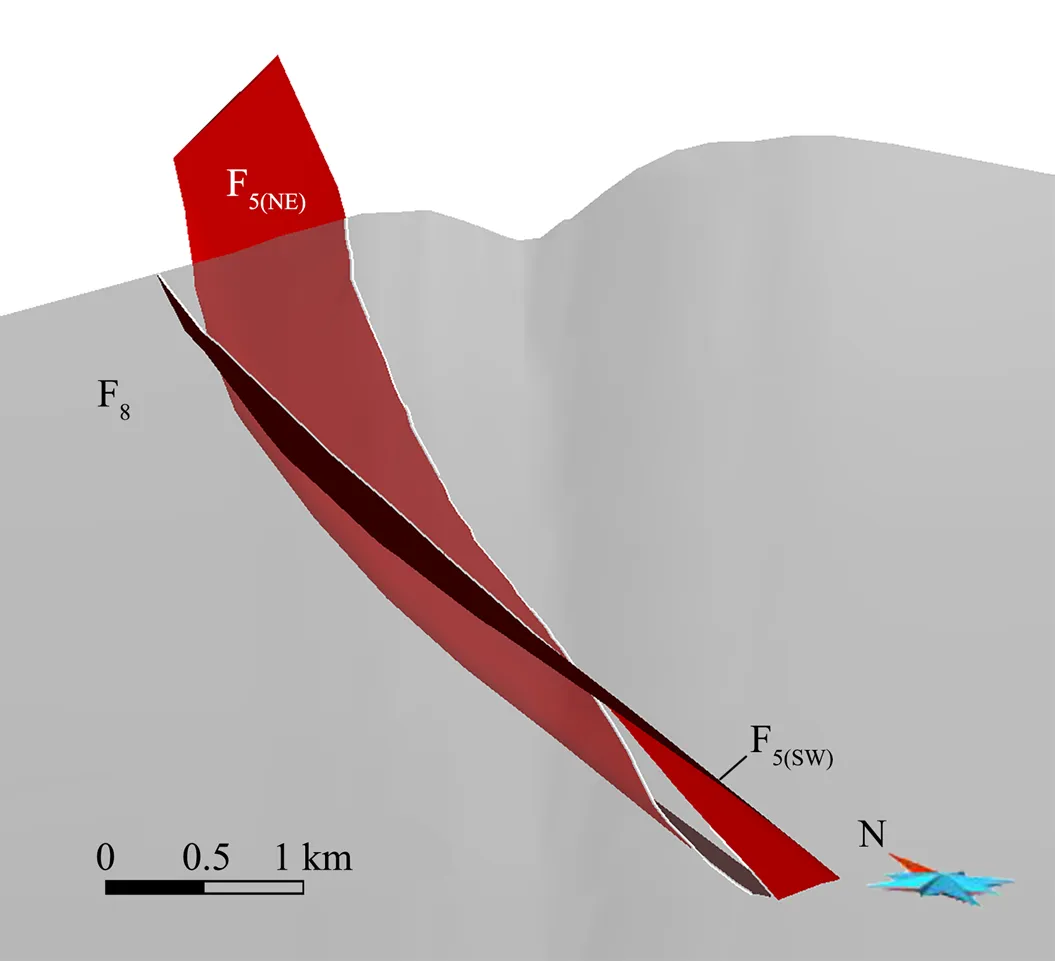
F5(NE)为断层F5北东段, F5(SW)为断层F5南西段, 白色线为断层F5与F8交线, 向NE看。

4.2 断层线平移连接与顺延连接对比

进行整体法建模, 需要对地表断层线进行连接, 前文采用了顺延连接, 兹讨论平移连接方法及其建模效果。以F5断层为例, 该断层由北向南被NW向断层切割为5段, 记为a、b、c、d、e; 保持c段位置不变, b、a段依次向SE平移, d、e段依次向NW平移, 与c段连接, 得F5完整断层线; 生成系列断层线, 建立初始断层面, 求取断后约束条件, 交切处理及约束插值, 建立模型。

通过对比, 认为该方法存在断层面整体偏移误差, 通过约束插值仍然无法消除。虽然借助地表断层线约束, 可将地表位置的曲面插值拟合至原始数据, 但在其他高程上, 断层面仍然存在整体偏移, 即F5的南西段向NW偏, 北东段向SE偏(图12)。该误差源自各段地表断层线平移, 并传导至系列断层线和断层曲面。而顺延连接方法对F5断层线的修改仅限于各段断点及其附近节点, 并可通过约束插值进行消除, 建模效果较好。

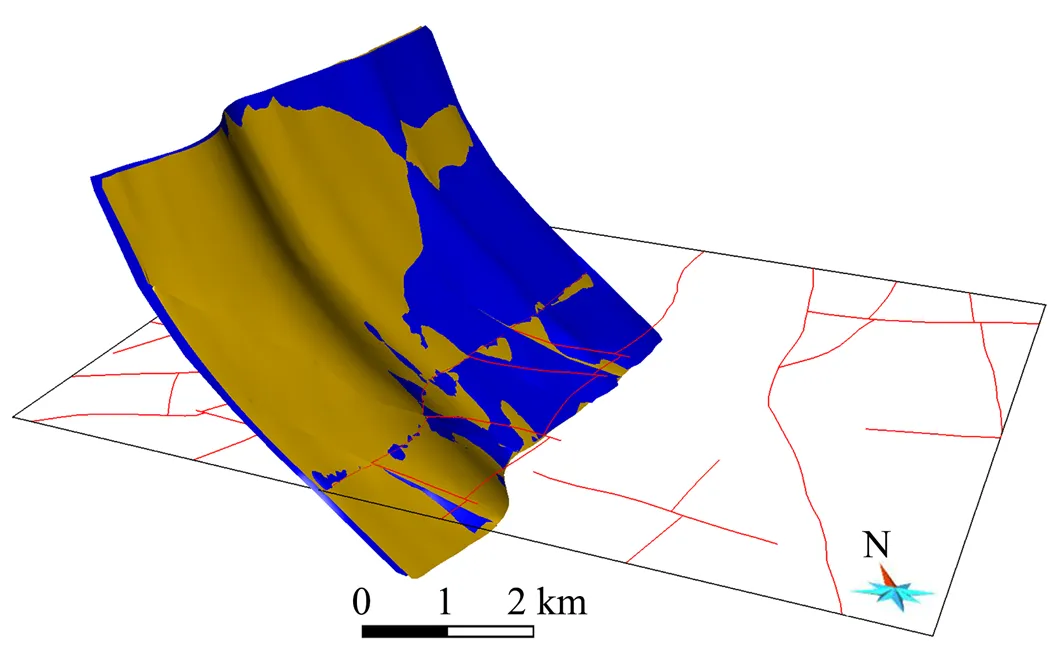
黄色面为断层线顺延连接所建模型, 蓝色面为断层线平移连接所建模型, 红色线为地表断层线。

4.3 断层面完全切割与部分切割对比

建模过程中, 依产状将地表断层线沿倾向延伸、建模, 常导致地表未交切断层在其他高程发生交切, 形成部分切割关系, 这一现象在缓至中等倾斜断层区的表现尤为明显。因部分切割关系的建模具有难度, 简化起见, 尝试将切割断层沿走向顺延, 形成完全切割。通过与原始建模数据对比, 认为断层曲面存在过度延伸问题(图13), 不难推断, 对于多组断层建模, 此方法会造成不同方向断层的“攀比式”顺延, 导致所有切割断层均延伸至模型边界, 大大背离原始建模数据。可见, 断层建模中, 部分切割关系往往不可避免, 应遵从地质事实开展建模工作; 若须将断层面沿走向延伸, 则应基于断层规模、标志层特征、位移量等参数的研究认识, 慎重进行。

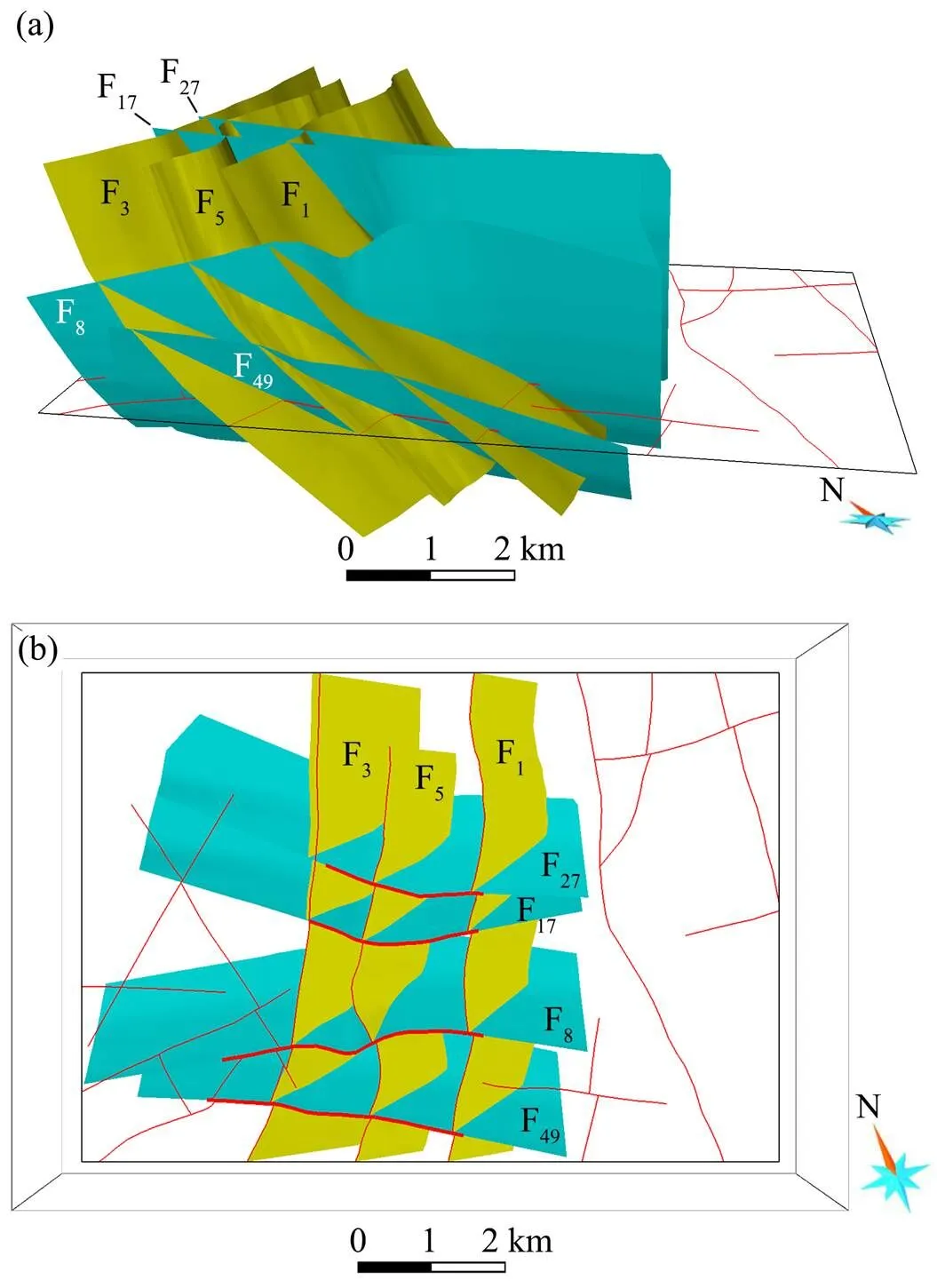
(a) NW向断层对NE向断层的完全切割, 向北东平视; (b) NW向断层面与地表断层线的对比, 断层面大大超出地表断层线。观察框水平剖切至地表。

此外, GOCAD软件自带的构造建模工作流(workflow)功能具有交互性好、建模精度高等特点, 对于交切断层等复杂地质体建模具有借鉴意义。

5 结论及展望

本文以广西珊瑚矿田为例, 探讨了基于地表数据和产状数据的交切断层建模方法, 通过对关键环节的不同建模方法的对比试验研究, 形成了如下认识:

(1) 采用地表断层线‒剖面断层轨迹‒系列断层线‒断层面的路线进行切割断层建模; 在切割断层建模路线的基础上, 采用建立初始断层面‒求取断后约束条件‒交切处理‒约束插值的路线进行被切割断层建模。

(2) 在断后约束条件的求取上, 以旋转法求取部分切割断层的错开部位约束, 以平移法求取完全切割断层的错开部位约束; 约束插值方面, 以断层错开部位约束、地表断层线约束及断层面边界约束为控制条件, 进行断层面DSI插值, 实现断层错动。

(3) 通过对比建模试验认为, 局部法建模存在断层走向延伸可控性差的问题, 分段断层线的平移连接会引起断层面的整体偏移误差, 过度追求完全切割关系建模将导致断层沿走向的过度延伸, 因此, 在上述三个关键环节上, 本文优选整体法建模、分段断层线的顺延连接及遵从原有切割关系的建模处理方法。

(4) 本文通过人机交互的方式建立模型, 若能基于计算机编程及软件平台的二次开发, 自动拟合断层曲面方程并求取插值约束条件, 将有助于建模效率的较大提升。此外, 若将模型用于地质过程数值模拟, 还须在断层格架的基础上建立地层曲面模型, 并对整个模型进行拓扑一致性检验、节点调整(网格尺寸控制)及二次重构, 以获得计算用网格模型, 相关工作将作它文另述。

致谢:两位审稿专家中南大学刘亮明教授及合肥工业大学李晓晖副教授为本文提出了宝贵的意见和建议, 使论文质量得到了很大的提升, 在此致以诚挚的谢意。

桂林矿产地质研究院. 2008. 广西钟山县珊瑚钨锡矿区工作程度图.

贾卓, 刘四新, 赵雪然, 鹿琪, 李宏卿, 王元新. 2021. 起伏地表下的复杂三维地质模型建立与重力异常计算. 吉林大学学报(地球科学版), 51(1): 277–285.

刘光伟, 宋佳琛, 白润才, 李鹏. 2018. 基于Morphing方法的断层面重构. 重庆大学学报, 41(2): 69–77.

舒良树. 2012. 华南构造演化的基本特征. 地质通报, 31(7): 1035–1053.

舒良树, 陈祥云, 楼法生. 2020. 华南前侏罗纪构造. 地质学报, 94(2): 333–360.

宋慈安. 2001. 珊瑚钨锡矿床. 北京: 北京工业大学出版社: 1–159.

宋忠航, 冯阳, 施龙青, 许磊, 高为富, 潘超. 2015. 矿井小断层延伸长度定量化预测在麻黄井田的应用. 煤炭技术, 34(8): 58–60.

孙劲光, 高天鹏. 2016. 地质断层三维建模的表达式方法. 地球信息科学学报, 18(10): 1322–1331.

王统, 田宜平, 罗莹莹, 张睿. 2020. 基于地质大数据与构造语义约束的断层建模. 地质科技通报, 39(4): 69–75.

韦昌山, 熊成云, 刘国庆. 1993. 广西钟山珊瑚矿田的构造变形、动力学演化与控矿关系. 广西地质, 6(4): 63–76.

吴立新, 史文中, Gold C. 2003. 3D GIS与3D GMS中的空间构模技术. 地理与地理信息科学, 19(1): 5–11.

熊天鹤, 袁红旗. 2018. 3Dmove模拟构造裂缝预测技术在川西新场构造须二段中的应用. 矿产勘查, 9(6): 1276–1280.

张慧, 潘懋, 曹凯, 郭艳军, 李珀任. 2018. 复杂断层网建模关键技术. 科学技术与工程, 18(20): 281–285.

朱良峰, 潘信. 2008. 地质断层三维构模技术研究. 岩土力学, 29(1): 274–278.

邹艳红, 李高智, 毛先成, 陈玉婷. 2020. 基于隐函数曲面的三维断层网络建模与不确定性分析. 地质论评, 66(5): 1349–1360.

Cherpeau N, Caumon G, Lévy B. 2010. Stochastic simulations of fault networks in 3D structural modeling., 342(9): 687–694.

Duvinage I. 2000. Creation and consistency of structural models from horizons extracted from three-dimensional seismic data (in French). Nancy: Institut National Polyte­chnique de Lorraine PhD thesis: 1–167.

Galera C, Bennis C, Moretti I, Mallet J L. 2003. Construction of coherent 3D geological blocks., 29(8): 971–984.

Gillespie P A, Walsh J J, Watterson J. 1992. Limitations of dimension and displacement data from single faults and the consequences for data analysis and interpretation., 14(10): 1157–1172.

Guo J T, Wu L X, Zhou W H, Li C L, Li F D. 2018. Section- constrained local geological interface dynamic updating method based on the HRBF surface., 107: 64–72.

Hoffman K S, Neave J W, Nilsen E H. 2007. Beyond the Y-A solution to modeling half-Y and half-λ faults in structuralframeworks., 26(1): 1402–1046.

Li X F, Xiao R, Feng Z H, Wei C X, Tang Y W, Bai Y P, Zhang M G. 2015. Ar-Ar ages of hydrothermal muscovite and igneous biotite at the Guposhan-Huashan district, Northeast Guangxi, South China: Implications for Mesozoic W-Sn mineralization., 65(2): 160–176.

Mallet J L. 1992. Discrete smooth interpolation in geometric modeling., 24(4): 178–191.

Mao J W, Cheng Y B, Chen M H, Pirajno F. 2013. Major types and time-space distribution of Mesozoic ore deposits in South China and their geodynamic settings., 48(3): 267–294.

Tertois A L, Mallet J L. 2007. Editing faults within tetrahedralvolume models in real time.,,, 292(1): 89–101.

Wang D Z, Shu L S. 2012. Late Mesozoic basin and range tectonics and related magmatism in Southeast China., 3(2): 109–124.

Wu Q, Xu H. 2003. An approach to computer modeling and visualization of geological faults in 3D., 29(4): 503–509.

Wu S G, Wang X L, Ji Y X, Liu Y Z, Han W G. 2005. Application of forecasting structural cracks technique of 3DMove in Chengdao buried hill.(), 48(9): 1403–1410.

Zanchi A, Francesca S, Stefano Z, Simone S, Graziano G. 2009. 3D reconstruction of complex geological bodies: Examples from the Alps., 35(1): 49–69.

Zhang D, Zhao K D, Wang B D, Cheng K D, Luo X L, Zhang W, Li Q, Jiang S Y. 2020. Cretaceous granitic magmatism and mineralization in the Shanhu W-Sn ore deposit in the Nanling Range in South China., 126(6): 1–18.

Zou Y H, Liu Y, Pan Y, Yang K D, Dai T G, Mao X C, Lai J Q,Tian H L. 2019. Numerical simulation of hydrothermalmineralization associated with simplified chemical reactions in Kaerqueka polymetallic deposit, Qinghai, China., 29(1): 165–177.

Study on Modelling Method of Intersecting Faults Based on Surface and Occurrence Data

ZHAO Yilai1, 2, 3, ALISON Ord3, TANG Jingru1, 2, HU Rongguo1, 2, YANG Qijun1, WANG Jincao1, WANG Benda4

(1. Guangxi Key Laboratory of Exploration for Hidden Metallic Ore Deposits, School of Earth Sciences, Guilin University of Technology, Guilin 541004, Guangxi, China; 2. Collaborative Innovation Center for Exploration of Nonferrous Metal Deposits and Efficient Utilization of Resources, Guilin University of Technology, Guilin 541004, Guangxi, China; 3. Centre for Exploration Targeting, School of Earth Sciences, Universityof Western Australia, Perth, WA 6009, Australia; 4. Pinggui Feidie Co. Ltd., China Nonferrous Metal Mining Group, Hezhou 542800, Guangxi, China)

3D geological modelling is one of the powerful tools for geological research. The modelling of faults is more complicated than that of other geological bodies, especially in the modelling of a fault partly cutting and offsetting another one. Taking the Shanhu orefield as an example, this paper studies the methods of modelling the intersecting faults based on their surface and occurrence data. The cutting faults are modelled based on the technical route of fault curves on the surface, fault trajectories on cross section, series of curves, and fault surface. The cut faults are modelled based on the route of initial fault surface, post-fault constraints, faults cutting, and interpolation under constraints. In addition, other modelling methods are also tried for comparison and the following understandings are reached: (1) By rotating or translatinga cut fault surface from its initial position to the post-fault position followed by the cutting operation, the splitting position constraints of the cut fault are obtained. Discrete smooth interpolation on the fault surface is carried out to realize fault dislocation constrained by the splitting borders, fault curves on the surface, and the fault frame. (2) Modelling from parts of a fault (namely the part method) may result in poor controllability in the extension of segmented fault surfaces; Recovery of the offset fault curves through curve translation will cause overall offset error in the resultant fault surface; Excessive pursuit of fully cutting relation may lead to overextension of faults along their strike. Therefore, this paper adopts the methods of modelling each fault as a whole (namely the overall method), recovering the segmented fault curves by moving and connecting the nodes, and verifying the original cutting relationship, which show reasonable modelling results. It is expected that the understandings could contribute ideas to the modelling of intersecting faults and of strata cut by faults as well.

3D geological modelling; intersecting faults; partly cutting relationship; interpolation under constraints; Shanhu orefield

2021-11-29;

2022-05-08;

日期: 2023-09-28

国家自然科学基金项目(42362008)、广西自然科学基金项目(2018GXNSFFA281009、2020GXNSFAA297049)和广西科技创新基地建设类项目(桂科ZY21195031)联合资助。

赵义来(1982–), 男, 副教授, 从事三维地质建模及成矿数值模拟研究。E-mail: zyl@glut.edu.cn

P628

A

1001-1552(2023)06-1256-011

10.16539/j.ddgzyckx.2023.01.305