基于PCA-DEA-Tobit 模型的物流企业绩效评价
郭 瑛
(芜湖职业技术学院 经济管理学院,安徽 芜湖 241003)
我国经济目前正处于高速发展的阶段,国内货物的运输量和周转量与日倍增,而自加入WTO 以来,外企大规模进入中国市场,也导致竞争变得日益激烈。因此,构建科学的物流企业绩效评价体系对于物流企业制定战略、调整发展方向,并在激烈的市场竞争环境中占据优势地位具有重要意义。
近年来,对物流企业的绩效评价研究包括面向物流系统建立的指标评价体系[1]、基于层次分析法(AHP)方法的绩效评价模型[2-3]等。基于AHP 的方法主要由决策者进行主观评分并以此建立成对比较矩阵,因过于主观,而忽略了客观数据的重要性。此外,数据包络分析法(DEA)也是物流企业绩效评价中应用较多的一种方法,可以用来分析影响生产效率的因素,以提供相应的改进方向[4-5]。现有文献中基于DEA 方法的研究包括物流企业绩效[6]、基于DEA/超效率DEA/交叉效率DEA 和AHP/IAHP 的各种绩效评价[7-8]等。然而,传统DEA 方法(C2R-DEA 和BC2-DEA)存在固有缺陷,即在自评中为了最大化其评价值,某些指标会获得不现实的权重分配。此外,上述很多研究都未能满足应用DEA 的两个重要条件[9],即被评价单元的总数应在输入和输出指标数之和的两倍以上,且输入/输出指标之间不应存在强相关性。本文的前瞻研究[6]虽然有效解决了DEA 的使用前提问题,但未能区分内部因子指标和外部因子指标,将部分由外部环境决定的且与物流企业具体运营环节无关的指标也纳入了物流企业绩效评价体系,一定程度上影响了各物流企业的最终整体绩效评价及排序的准确性。
鉴于以上方法的局限性,本文首先构建了包含内部因子指标和外部因子指标的新的绩效评价指标体系。为了满足DEA 的使用条件,首先对投入和产出的内部因子指标降维,常用的降维方法包括PCA、基于多项式内核函数的内核PCA(KPCA)[10]、潜在语义分析(LSA)[11]、稀疏随机投影(SRP)[12]、多维缩放(MDS)[13]和Isomap[14]等。鉴于PCA运行速度快且实现较为简单,本文采用PCA 消除原二层内部因子指标之间的相关性,并按照至少85%的累计贡献率提取出新的二层指标并进行正数化处理,进而应用交叉效率DEA 评价各内部因子一层指标,并和由熵权法得到的客观权重相结合,以得到各决策单元的整体绩效值及相应排序,最后以Tobit 回归模型分析外部因子指标与物流企业整体绩效的关联程度及其影响。PCA-DEATobit 模型以客观数据为基础,因此能规避各类主观评分给绩效评价带来的负面影响。
1 绩效评价指标体系
物流系统属复杂系统,指标选择上应贯彻全面性、客观性和可比性,并使选取的指标系统化。本文的决策单元为待评价的物流企业(DMUi),借鉴王瑛等基于两阶段的物流系统综合评价中的数据[1]建立多层次综合指标体系,如图1 所示。依据各指标与物流企业具体运营环节的关联与否,本文将文献[1]中的指标区分为内部因子指标和外部因子指标。(1)内部因子指标关联的是物流企业内部的具体运营环节,包括运输、仓储、库存、经营信息化四个一层指标,并将其进一步区分为与物流企业运营环节契合的二层指标。在二层指标中,依据DEA 算法,将越小越好和越大越好的指标分别定义为投入指标(I 开头)和产出指标(O 开头)。(2)外部因子指标是指与外部环境(例如市场、经济环境等)相关,且可能影响物流企业整体绩效的外部影响因素,主要考虑文献[1]中提供的指标,选取净资产利润率、总资产利润率、资金周转率和市场占有率四项指标,并通过Tobit 回归法分析以上指标与物流企业整体绩效的关联程度及影响程度。

图1 多层次绩效评价综合指标体系Fig.1 Comprehensive multi-level indicators system for performance evaluation
2 基于PCA-DEA-Tobit 的评价方法的构建
2.1 主成分分析法(PCA)
PCA 可以在尽量避免信息损失的前提下从多个相关变量中提取出起主导作用且互不相关的少数几个变量。本文的多层次绩效评价综合指标体系中,二层指标所代表的信息可能有所重叠,且由于各一层指标下的投入/产出二层指标数量和决策单元数量相比过大,因此先使用PCA 消除原二层指标之间的相关性,并按照至少85%的累计贡献率提取出相应的新指标。
2.2 交叉效率DEA 法
在传统和超效率DEA 中,在自评的过程中为了最大化其评价值,某些指标会被赋予不现实的权重分配,导致最终的评价结果不够公平客观。因此,Sexton 等在传统CCR 模型的基础上提出了交叉效率DEA[15],某决策单元DMUd相对于决策单元DMUj的交叉效率见式(1)。
其中,μrj、ωrj分别为CCR 模型以决策单元DMUj为待评价对象时的第r个产出权重和第i个投入权重。而交叉效率评分则通过对决策单元等权集成,即算术平均的方式获得,即:
本文拟运用交叉效率DEA 来避免仅靠自评体系进行评价的弊端,同时用自评和他评评价所有决策单元中各个一层指标的相对效率,得到的结果可进一步与熵权法相结合,以得到各评价单元的整体绩效评价。
2.3 熵权法
熵可用于评估事物无序程度及数据的有效信息量,熵值越小代表其有效性越高,反之越低。与需要决策者进行主观评分的AHP 方法相比,熵权法首先利用客观数据计算信息熵(即指标变异程度),再进一步确定指标权重。
2.4 Tobit 回归模型
Tobit 回归模型是一种因变量受限的回归模型[16],被广泛应用于计量经济学领域解决存在截断数据情况下的统计分析问题,近年来也常用于两阶段DEA-Tobit 模型分析[17]。由于通过DEA 模型计算出来的效率值属于截断的情况,其值在0 与1 之间且最大值为1,如果采用普通最小二乘法来估计回归系数,可能会出现因数据无法完整呈现而导致估计偏差的情况,因此,本文选取Tobit 回归模型来分析外部因子指标与物流企业整体绩效的关联程度及对其影响程度。见式(2)。
其中,Fi为第i个外部因子指标,即自变量,Performance为各决策单元的整体绩效值,即因变量,βi为绩效影响因素的对应系数,ε为随机干扰项。
2.5 基于PCA-DEA-Tobit 的新绩效评价模型
绩效评价的具体步骤如下:
步骤1:使用PCA 消除原二层指标之间的相关性,并按照至少85%的累计贡献率提取出相应的新二层指标并进行正数化处理,新投入指标以nin开头,新产出指标以nou 开头。
步骤2:根据新的二层指标,以交叉效率DEA评价各决策单元的一层指标,并得到各决策单元对各一层指标的相对效率值θij。
步骤3:以熵权法首先计算信息熵(即指标变异程度),再进一步确定所有二层指标的权重,最后以叠加方法得到所有一层指标的权重ωi。
步骤4:根据步骤2 和步骤3 计算得出的θij和ωi,得到各决策单元的整体绩效值
步骤5:以步骤4 的各物流企业综合绩效值为因变量,外部因子指标为自变量,验证相关性及计算相关系数。
3 实例分析
步骤1:使用IBM SPSS Statistics 25.0 软件对原二层指标进行PCA分析,在应用PCA之前,需要:(1)进行KMO 检验,以检查指标之间的相关性及偏相关性;(2)进行巴特利球体检验,验证指标数据的分布及指标间的独立情况。其中,KMO 值越大,代表变量之间的相关性越强,越适合使用PCA,反之,当KMO 值小于0.5 时,不应使用PCA。巴特利球体检验得到的Sig.值应小于0.05,且越小越好。以一层经营信息化指标下面的四个二层产出指标,即实时信息的传输量/信息化投资(O13),网络覆盖率(O14),客户变动的完成率(O15)和平均事后用户满意率(O16)为例,如表1 所示,KMO 值为0.738,且Sig.值为0.013,因此适合应用PCA 进行主成分提取。

表1 KMO 和巴特利球体检验Tab.1 KMO and Bartlett’s Test
同理,如表2 和表3 所示,对其他二层投入和产出指标成功进行KMO 检验和巴特利球体检验之后,分别应用PCA 并按照累计贡献率大于85%得到因子得分系数矩阵,可得出新的二层投入指标和产出指标。通过PCA,每个一层指标下的新投入指标和新产出指标各为两个,而决策单元数目为八个,满足了继续进行DEA 分析的前提。
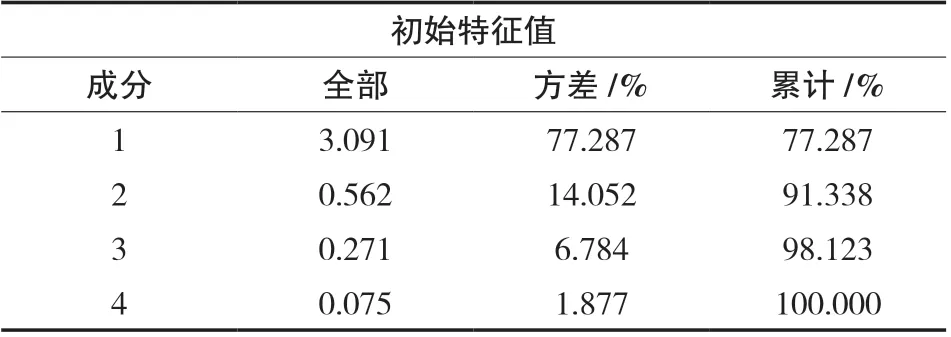
表2 总方差解释Tab.2 Total Variance Explained
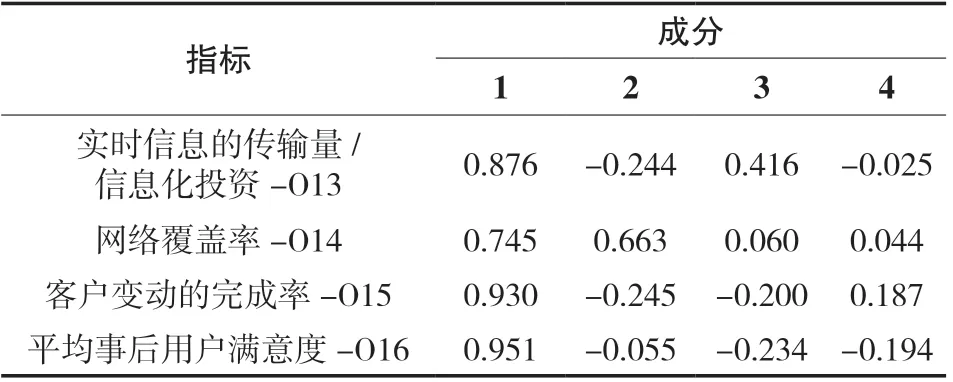
表3 成分矩阵aTab.3 Component Matrix
经PCA 处理后,部分新二层指标为负数,因而需要进行正数化处理以满足DEA 运算要求。正数化处理常用方法包括幂指数或减去负数指标向量中的最小值。然而,幂指数方法不适合数据相近的情况,而减去最小值的方法则会产生零值,均不适合DEA。因此,本文采用式(3)的正数化处理方法[18],得到经过正数化处理后的新二层投入/产出指标值。
其中:xj'为表3 中有负数的投入或产出指标向量,xj则是正数化处理后的新的投入或产出指标。
步骤2:基于经过正数化处理后的新二层投入/产出指标值,应用数学软件MATLAB 2017b 对决策单元的一层指标进行交叉效率DEA 分析,其中一层经营信息化指标的交叉评价矩阵如下:
矩阵中,主对角线元素是各决策单元在经营信息化指标上自我评价的效率值,其中,自我评价达到最大值1 的DMU1,DMU3,DMU6,DMU7 都是相对有效的,然而无法对它们进行优劣排序,因此需计算其交叉效率值(即列向量平均值)加以分析,结果见表4。在一层经营信息化指标上,各决策单元的效率优劣排序为:DMU7>DMU3>DMU6>DMU1>DMU5>DMU8>DMU2>DMU4。

表4 一层经营信息化指标的交叉效率值Tab.4 Cross-efficiency values of first-level management informatization indicator
同理,对其他一层指标进行类似计算,可得到表5。

表5 所有一层内部因子指标的交叉效率值Tab.5 Cross-efficiency values of all first-level internal factor indicators
步骤3:基于经过正数化处理后的新二层投入/产出指标值,应用数学软件MATLAB 2017b 计算得出所有二层指标的权重,并通过叠加方式计算得出各一层指标权重,见表6。

表6 熵权指标权重Tab.6 Entropy weight indicators weight
步骤4:根据表6 的指标权重及表5 的交叉效率值,计算得到各决策单元的整体绩效评价及排序,见表7。

表7 整体绩效评价及排序Tab.7 Overall performance evaluation and ranking
步骤5:Tobit 回归分析。因变量为步骤4 得到的各物流企业的最终绩效;自变量方面,为了避免数据存在异方差性,对外部因子指标净资产利润率(F1)、总资产利润率(F2)、资金周转率(F3)、市场占有率(F4)进行对数变换之后,运用Stata 17.0完成上述回归模型的计算,并得到结果如表8 所示。从结果来看,因P值均小于0.005,所以模型拟合程度良好,回归结果真实有效。其中,净资产利润率(F1)、总资产利润率(F2)和市场占有率(F4)均在1%水平上显著,系数为正。从相关系数来看,市场占有率(F4)对物流企业绩效的正面影响是净资产利润率(F1)或总资产利润率(F2)的数倍,符合预期。此外,分析结果显示,资金周转率(F3)在1%的水平上显著但系数为负,然而因本文仅分析了8 个物流企业,样本有限,因此资金周转率(F3)的弱负相关性还有待增加样本数量,进一步研究确认。
4 结论
基于现有文献的欠缺之处,提出了一个基于PCA-DEA-Tobit 的物流企业绩效新评价方法,并以实证验证了其有效性和可行性。(1)将物流企业绩效的指标分为内部因子指标和外部因子指标,内部因子指标关联的是物流企业内部的各个运营环节,而外部因子指标指与外部环境(例如市场、经济环境等)相关且可能影响物流企业整体绩效的外部影响因素;(2)以PCA-交叉效率DEA 结合熵权法的绩效评价方法模型对文献[1]中的8个决策单元进行了整体绩效评价和排序;(3)使用Tobit 回归模型分析了外部因子指标与物流企业整体绩效的关联程度及其影响,发现净资产利润率、总资产利润率和市场占有率均在1%水平上显著且系数为正,资金周转率在1%的水平上显著但系数为负,其中,市场占有率的相关系数对物流企业绩效的正面影响是净资产利润率或总资产利润率的数倍,符合预期。本文提出的基于PCA-DEATobit 物流企业绩效评价方法模型以客观数据为基础,有助于指导物流企业整体绩效的战略调整。一方面,交叉效率DEA 通过互评体系得到的效率值是相对客观的,这是因为传统DEA 和超效率DEA在自评的过程中为了最大化其评价值,某些指标会被赋予了不现实的权重分配从而导致效率值被高估。另一方面,与需要决策者主观评分的AHP 方法相比,熵权法从客观数据中确定各指标权重,以衡量各个指标对评价结果的影响程度,可以有效消除主观因素带来的负面影响。
本方法对提高物流企业整体绩效具有较强的指导意义,例如表2 可通过横向对比,确认各个决策单元在某一层指标的优劣和排序,并追踪相对薄弱的二层指标;而通过纵向对比可以发现严重影响本决策单元整体绩效的弱势一层指标,例如DMU4的经营信息化及DMU8 的运输。得到的薄弱指标或环节可视为绩效改善的重点方向。此外,本方法还可有效分析外部因子指标与物流企业整体绩效的关联程度及其影响。不足之处在于本文的建模及绩效评价分析均基于文献[1]中的数据,因此研究结果受限于文献中物流企业的样本数量及该文献所提供的评价指标,具体而言:(1)文献中的8个物流企业或许难以充分代表整个物流行业的特点和规律;(2)外部因子评价指标仅包含部分财务和市场的评价因素,不够全面。因此,本文作者将在后续的研究中收集更多的物流企业样本以及更详细的绩效评价指标,以期进一步验证该模型在物流企业绩效评价中的普适型和可推广性。

