受脉冲扰动的多智能体系统的有限时间平均一致性
耿晓鹏,吕晓晓
(青岛大学 自动化学院,山东 青岛 266071)
多智能体系统作为人工智能研究的基本对象受到了国内外研究者的广泛重视。由于其鲁棒性、可靠性及高效性,多智能体系统已广泛应用于计算机网络、电力系统、交通控制和军事等众多领域[1-3]。其中,分布式协调控制是多智能体系统的一个基础研究问题,包括追踪[4]、群集[5]、分布式滤波器[6]、可控性[7]和一致性[8]等。其中,一致性是多智能体系统的最基本问题,它描述了同一系统中每个智能体在预先设定的控制协议下可以达到某种状态[9-11]。在现有的一致性结果中,大多数多智能体系统在一致性控制协议下实现了渐近/指数收敛,这意味着系统只有在无限的时间内才能逐步达到稳定。在实际的工程系统中,如航天系统、机器人控制系统等短时间工作的系统,往往需要的是系统能够在有限的时间内达到渐近稳定[12]。因此,多智能体系统有限时间一致性问题引发了大批国外学者的研究兴趣,相关研究结果被提出[13-16]。
另一方面,网络拓扑在多智能体系统一致性问题的研究中发挥了至关重要的作用。为了获得更好的收敛速度,对于一些特殊的交互图,如包含有向生成树的有向图和强连通的有向图,许多学者都在寻找更好的代数连通性。在实际应用中,通讯干扰或者超出通讯范围都可能会导致智能体之间的通讯中断,同时,又可能在任意两个智能体之间重新建立新的通信链路,这意味着智能体之间的拓扑将随着时间的推移而改变[17]。因此,进一步研究具有切换拓扑的多智能体系统的有限时间一致性具有重要意义[18-20]。
在许多实际情况下,系统在某些时刻可能会遇到一些突变,其状态不再是连续的动态演化,这种突变被称为脉冲现象。近年来,具有脉冲效应的多智能体系统在脉冲微分方程下有着广泛的研究[21-23]。不难发现,脉冲效应对系统的稳定性具有双面性,可分为镇定的脉冲和去稳定的脉冲。一方面,镇定的脉冲是指脉冲控制是一种成本低、鲁棒性强的有效控制策略。因此,基于脉冲控制的多智能体系统的一致性问题近年来被国内外学者们大量的研究[24-26]。另一方面,去稳定的脉冲可以看作是脉冲扰动,这意味着无脉冲效应的系统本身具有一定的稳定性,在脉冲扰动下仍能保持相应的稳定性。由于脉冲扰动对系统的动力学行为有很大的影响,因此研究脉冲扰动对多智能体系统一致性的影响是非常有必要的[27-28]。到目前为止,受扰动的多智能系统的有限时间一致性已有较多结果,但关于脉冲扰动的结论还相对较少。多智能体系统在到达停息时间之前受到脉冲扰动,将会延长原来的停息时间,这激发了我们的研究兴趣。本文研究了脉冲扰动下具有切换拓扑的多智能体系统的有限时间平均一致性问题。主要创新点如下:
1)在多智能体系统的有限时间平均一致性研究中考虑了脉冲扰动,且所研究的是脉冲扰动次数对停息时间的影响,因此脉冲效应只在多智能体系统达到停息时间之前施加。
2)利用Lyapunov 有限时间稳定性定理、代数图论和脉冲控制理论,推导出了具有脉冲扰动和切换拓扑的多智能体系统的有限时间平均一致性的充分条件,并对其停息时间进行了有效估计。
3)本文的停息时间取决于多智能体系统的初始条件、脉冲扰动次数及网络拓扑结构等多种因素。
本文的其余部分组织如下:第1 节给出了有限时间稳定性理论以及代数图论的相关知识;第2 节中介绍了具有脉冲扰动的多智能体系统有限时间平均一致性的主要结果;第3 节给出了一个数值例子;第4 节总结全文。
1 基础知识及模型介绍
在本节中,首先列出本文用到一些符号及代数图论的相关知识,然后是问题的描述。最后,给出了本文需要的引理。
1.1 符号
文中用到的主要符号如下:1n是一个元素全为1 的n 维列向量;R+(Z+)是正实数(整数)的集合;Rn具有Euclid 范数的n 维实空间;D+V(t)表示函数V:R→R 在t∈R 的右上Dini 导数,即:
1.2 图论
考虑由n 个智能体组成的多智能体系统,智能体之间的通信由有向图G=(V,ε,A)来描述,其中V={1,2,…,n}为节点集,节点i∈V 表示第i 个智能体,ε=V × V 为边集,A=[aij]∈Rn×n为邻接矩阵。如果(j,i)∈ε,则邻接矩阵A 中的元素aij不等于0,此时智能体i 是智能体j 的邻居;否则aij=0。智能体i 的邻居组成的集合为Ni={j∈V:(i,j)∈ε}。从智能体i 到智能体j 的有向路径为有限有序边序列,形式为(i,l1),(l1,l2),…,(lk-1,lk),(lk,j)。在有向图中,如果存在一个节点(即根节点),且满足从根节点到任何其他节点至少存在一条有向路径,那么则称该有向图包含一个有向生成树。定义与G 相关的Laplace 矩阵L=[lij]∈Rn×n,如果i≠j,则lij=-aij,且若有向图中所有的入度等于出度,即对于所有的则称有向图是平衡的。
1.3 问题陈述
考虑由n 个相同的智能体组成的多智能体系统,第i 个智能体的状态可以描述为
其中:xi(t)∈R,i∈V 表示系统状态;ui(t)∈Rn表示控制输入;wi(t)为脉冲扰动。wi(t)形式为
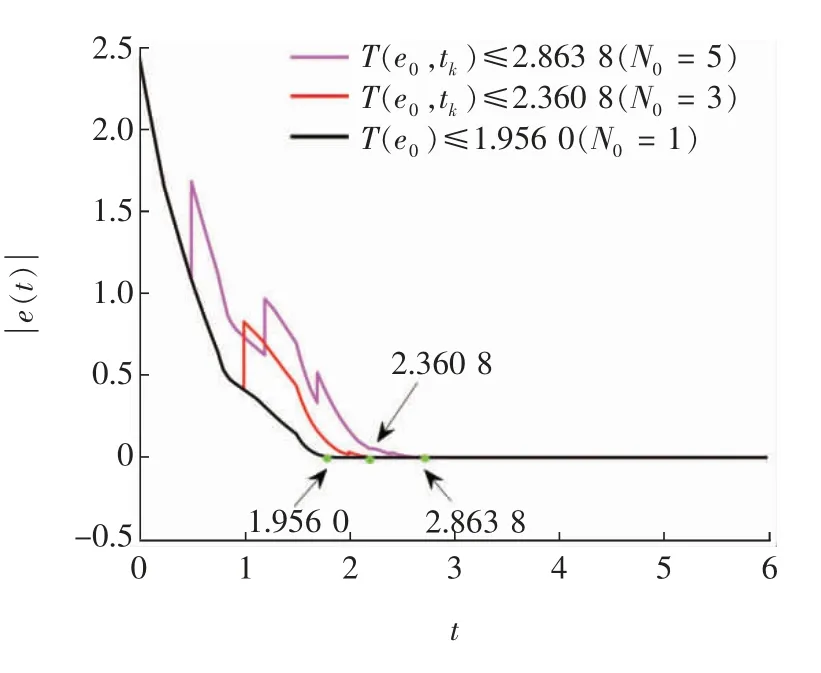
其中:dk>0 为脉冲扰动系数,k∈Z+;δ(·)为Dirac函数。序列S={tk,k∈Z+}是满足0=t0 将系统(1)改写为 引理1[1]设L 为有向图G 相关联的Laplace矩阵,如果G 包含有向生成树,则0=λ1(L)<λ2(L)≤λ3(L)≤…≤λn(L),λ1n(L)=0 且Re(λ1(L))>0,i=2,3,…,n。 引理2[29]令x1,x2,…,xn≥0,0 考虑如下的脉冲控制系统: 其中,f(z(t)),f(z(t-))和z0的定义与文献[30]中的定义相同,这里省略。在此之后,我们建立以下引理。 引理3[30]如果存在正常数β >1,0 <η <1,α,δ 和两个K 类函数φ1,φ2和局部Lipschitz 连续的函数V(z):Ω →R+∪0 使得 考虑具有脉冲扰动和切换拓扑的多智能体系统(1)的有限时间平均一致性。设计如下的控制律: 其中:σ(t):R+→ρ={1,2,…,m}为分段常数信号,被称为切换信号为有向图Gσ(t)邻接矩阵中的元素,0 <γ <1。 假设1有向图Gi,i∈{1,2,…,m}是平衡的且包含有向生成树。 定理1若假设1 成立,存在常数γ∈(0,1),dk>0,β∈[1,∞),使得不等式 成立,则初始条件为ei(t0)∈Ωδ的多智能体系统(1)可以实现有限时间平均一致性,其中ei(t0)=xi(t0)-ξ(t0)且脉冲序列{tk}满足 则停息时间可估计为 类似地,可得Δξ(tk)=0。令ei(t)=xi(t)-ξ(t),则可以写出xi(t)和ξ(t)之间的误差系统为 考虑如下的Lyapunov 函数: 当t≠tk,k∈Z+时,计算V(t)沿误差系统(9)的状态轨迹的右上Dini 导数 根据引理1 和引理2,我们得到 当t=tk时,结合式(6)可以得到 显然,式(7)、(10)—(12)满足引理3 中的 所有条件,因此,受脉冲扰动(2)的多智能体系统(1)在控制协议(5)下可以实现有限时间平均一致性,其停息时间可由式(8)估计。 考虑具有6 个节点的多智能体系统(1),其可能的网络拓扑连接关系如图1 所示,其中网络拓扑每T=2.1 在4 种有向图中进行一次随机切换,显然假设1 成立。考虑系统(1)的参数为γ=0.2,dk=0.55,并且选取如下的脉冲时间序列:t4n-3=2.1n -1.6,t4n-2=2.1n -1.35,t4n-1=2.1n -0.6,t4n=2.1n(见图2)。令β=1.1,初值x0满足<δ=0.6,容易计算出=0.388 20。因此,由引理3(当N0=1 时)可知无脉冲扰动的多智能体系统(1)在控制器(5)下可以实现有限时间平均一致性,且停息时间可估计为T(x0)=1.956 0,如图3 所示。进一步计算可得:t7=3.6 >3.464 5=β6T(x0),则N0=7 成立,那么脉冲时间序列为 图1 切换的通信拓扑Fig.1 Switching communication topologies 图2 脉冲切换信号Fig.2 Impulsive switching signal 图3 无脉冲扰动的受控多智能体系统(1)的有限时间平均一致性(i=1,2,3,4,5,6)Fig.3 Finite-time average consensus for controlled multi-agent systems(1)without impulsive disturbances(i=1,2,3,4,5,6) 若定理1 中的所有条件都满足,则可以得到切换拓扑下具有脉冲扰动(2)的多智能体系统(1)可以实现有限时间平均一致性,且停息时间可估计为T(e0,(tk))=3.464 5,如图4 所示。另一方面,由于T(e0,(tk))=3.464 5 >T(e0)=1.956 0,这意味着在达到停息时间之前,有限次的脉冲扰动将延长系统(1)的未受扰动时的停息时间。 图4 带脉冲扰动的受控多智能体系统(1)的有限时间平均一致性(i=1,2,3,4,5,6)Fig.4 Finite-time average consensus for controlled multi-agent systems(1)with impulsive disturbances(i=1,2,3,4,5,6) 显然,脉冲扰动的个数对于停息时间的影响是显著的,因此分析参数的敏感性是非常有必要的。当选择N0=3,S2={1,2}时,容易计算出此时的停息时间为2.360 8。另外,当N0=5,S4={0.5,1.2,1.7,2.4}时,停息时间为2.863 8,对应的仿真如图5所示。因此,在到达停息时间之前多智能体系统受到脉冲扰动,会延长原来的停息时间,脉冲扰动次数越多,停息时间就越长。 图5 不同N0 时的停息时间Fig.5 The setting-time with different N0 本文研究了切换拓扑下受脉冲扰动的多智能体系统的有限时间平均一致性。利用Lyapunov 有限时间稳定定理、代数图理论和脉冲控制理论,得到了保证有限时间平均一致性的充分条件。在此基础上,根据多智能体系统的初始条件、脉冲扰动的数量及其网络拓扑结构,重新估算出停息时间。最后,通过数值算例对所得结果进行了仿真,验证了所得结果的有效性。1.4 带有脉冲扰动的有限时间稳定
2 脉冲扰动下有限时间平均一致性
3 仿真实例
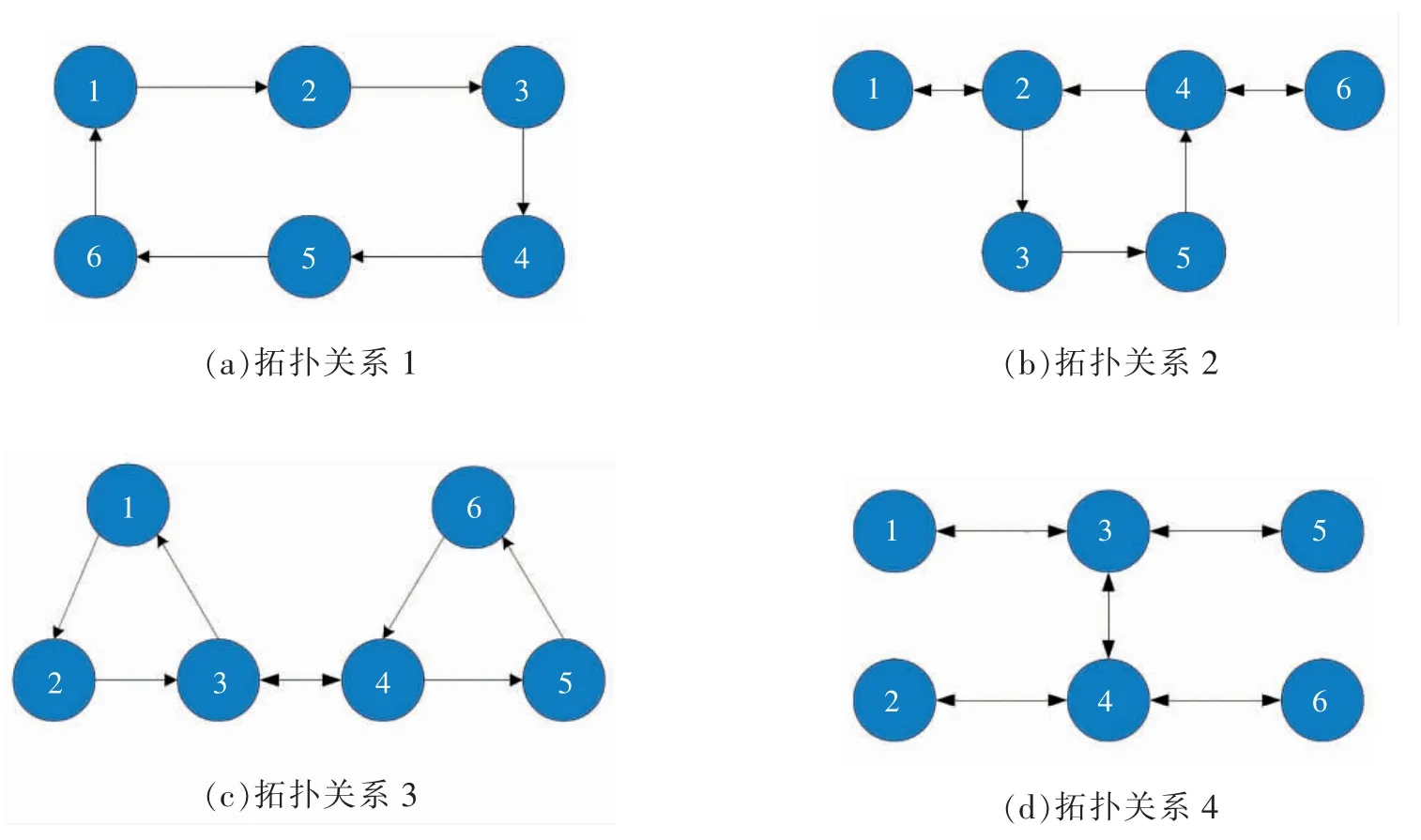
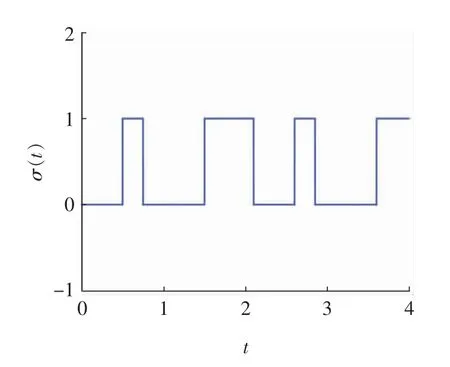
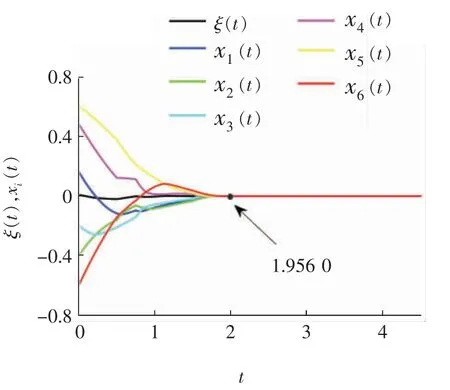
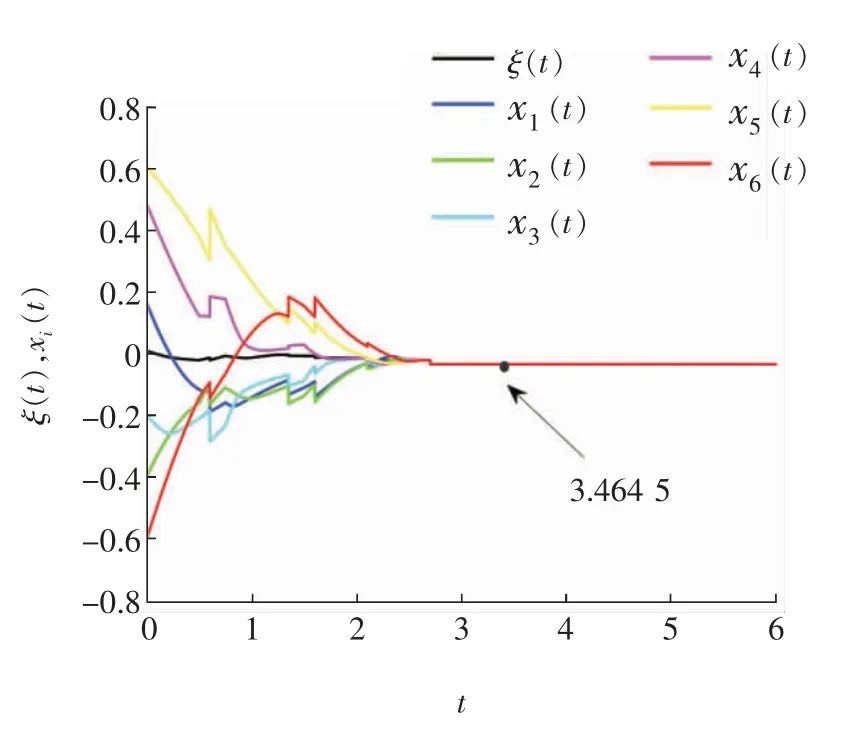
4 结论

