对增阻系数法计算浆体管道阻力的研究

刘德忠(中国恩菲工程技术有限公司, 北京 100038)

1 浆体管道流态判别

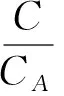
浆体相对体积浓度按H.M.伊斯梅尔方程计算[1]

(1)

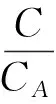
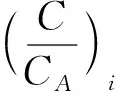
(2)

式中,-Zi为悬浮指数[2],去掉负号的Zi为沉降指数。

沉降指数为

(3)

浆体中粒径di的沉速ωi按表1刘德忠颗粒沉速公式表计算[3]

表1 刘德忠颗粒沉速公式表

(4)

达西摩阻系数λ按恩菲刘德忠公式计算

(5)

(6)

式中:ωi—浆体中粒径di的沉速,按表1恩菲刘德忠粒径沉速公式计算;K—修正卡门常数,K=0.36;β—伊斯梅尔系数,β=1;V*—摩阻流速,m/s;V—浆体输送设计流速,m/s;D—管道内径(m);λ—达西摩阻系数;ε—管道内壁粗糙度,mm,直缝新钢管ε=0.050 8～0.054 0 mm;Re —全部浆体宾汉体雷诺数;η—全部浆体浆体宾汉体刚度系数,η=f(CV)由试验得出(Pa·s);ρ—全部浆体浆体密度,kg/m3;λ1、Re1、η1、ρ1是似均质部分对应的参数。

浆体中似均质体积浓度C1V为

(7)

式中:CV—全部浆体浆体体积浓度;C1V—似均质浆体体积浓度。

浆体中非均质浆体体积浓度C2V为

(8)

式中:C2V—非均质体积浓度。

己知似均质体积浓度C1V,似均质浆体密度ρ1为

ρ1=ρgC1V+(1-C1V)ρs

(9)

式中:ρg—物料密度,kg/m3;ρS—水密度,kg/m3。

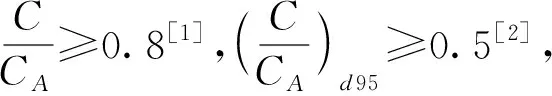
通过流态判别计算可得出以下浆体相对体积浓度

C1V+C2V=CV

(10)

(11)

通过对式(10)和式(11)的分析,提出动态粗细颗粒分界粒径概念和C2V非均质浆体体积浓度增阻概念。

2 粗细颗粒分界粒径的定义

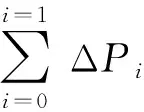
当物料粒径di≤d1m时,所有细颗粒的di体积浓度(C1V)i构成似均质体积浓度C1V,即:

C1V=∑(C1V)i

(12)

当物料粒径di≥d1m时,所有粗颗粒的di体积浓度(C2V)i构成非均质体积浓度C2V,即:

C2V=∑(C2V)i

(13)

d1m是粗细颗粒的分界,也是似均质体积浓度和非均质体积浓度分界,定义粗细颗粒分界粒径有助于对非均质阻力计算研究的深化。

3 浆体管道阻力计算

浆体管道阻力ik按下式计算

ik=i1+Δi2

(14)

式中,i1为C1V细颗粒似均质浆体管道阻力;Δi2为C2V粗颗粒非均质浆体管道阻力;Δi2为是增阻的主因。

C1V细颗粒似均质浆体管道阻力i1按下式计算

(15)

4 增阻系数的定义及对增阻系数公式的推导

4.1 增阻系数的定义

CV全部浆体管道阻力ik除以C1V细颗粒似均质浆体管道阻力i1,定义为增阻系数,符号为k2。

因为,式(14)变为

k2i1=i1+Δi2

(16)

将式(16)各项除以i1得

(17)

Δi2=i1(k2-1)

(18)

式(17)说明增阻系数k2是Δi2的函数,式(18)说明Δi2是k2的函数,二者互为函关系。

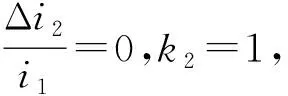
4.2 增阻系数公式的推导

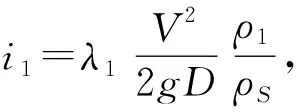
(19)

当di≥d1m时,我们取该段粗颗加权平均粒径d2P及沉速ω2P导出f2(d2P,ω2P,ρg,ρ1)被比较条件函数,k2i1为

(20)

将式(20)除以式(19)得增阻系数函数式为

(21)

式中,ω1m为沉速;d2P为粗颗粒加权平均粒径;ω2P为粗颗粒加权平均沉速。

式(21)主要参数是粒径和沉速,对粒径和沉速受力分析如下:

颗粒球体在浆体中沉降的有效重力为F1为

(22)

牛顿绕流阻力F2为

(23)

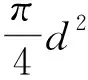
将式(23)除以式(22)得

(24)

对式(24)两边开方并进行量纲分析得Fr

(25)

式中,Fr为颗粒d与沉速ω的佛罗德数。

己知分界粒径d1m和沉速ω1m,得出分界粒径佛罗德数为

(26)

己知粗颗粒加权平均粒径d2P和粗颗粒加权平均沉速ω2P,得出粗颗粒加权平均粒径佛罗德数为

(27)

对于高中浓度浆体管道,增阻系数k2为

(28)

式中,指数n为

(29)

己知增阻系数,浆体管道阻力ik为

(30)

5 对增阻系数法浆体管道阻力计算公式的验证

采用增阻系数法计算浆体管道阻力公式对贵州瓷福磷精矿管道、山西太原尖山铁精矿管道、云南昆明大红山铁精矿管道、内蒙包头白云鄂博铁精矿管道、四川攀枝花市新白马铁精矿管道、巴布亚新新几内亚红土矿管道进行验证[4-5],具体管道阻力数据详见表2。

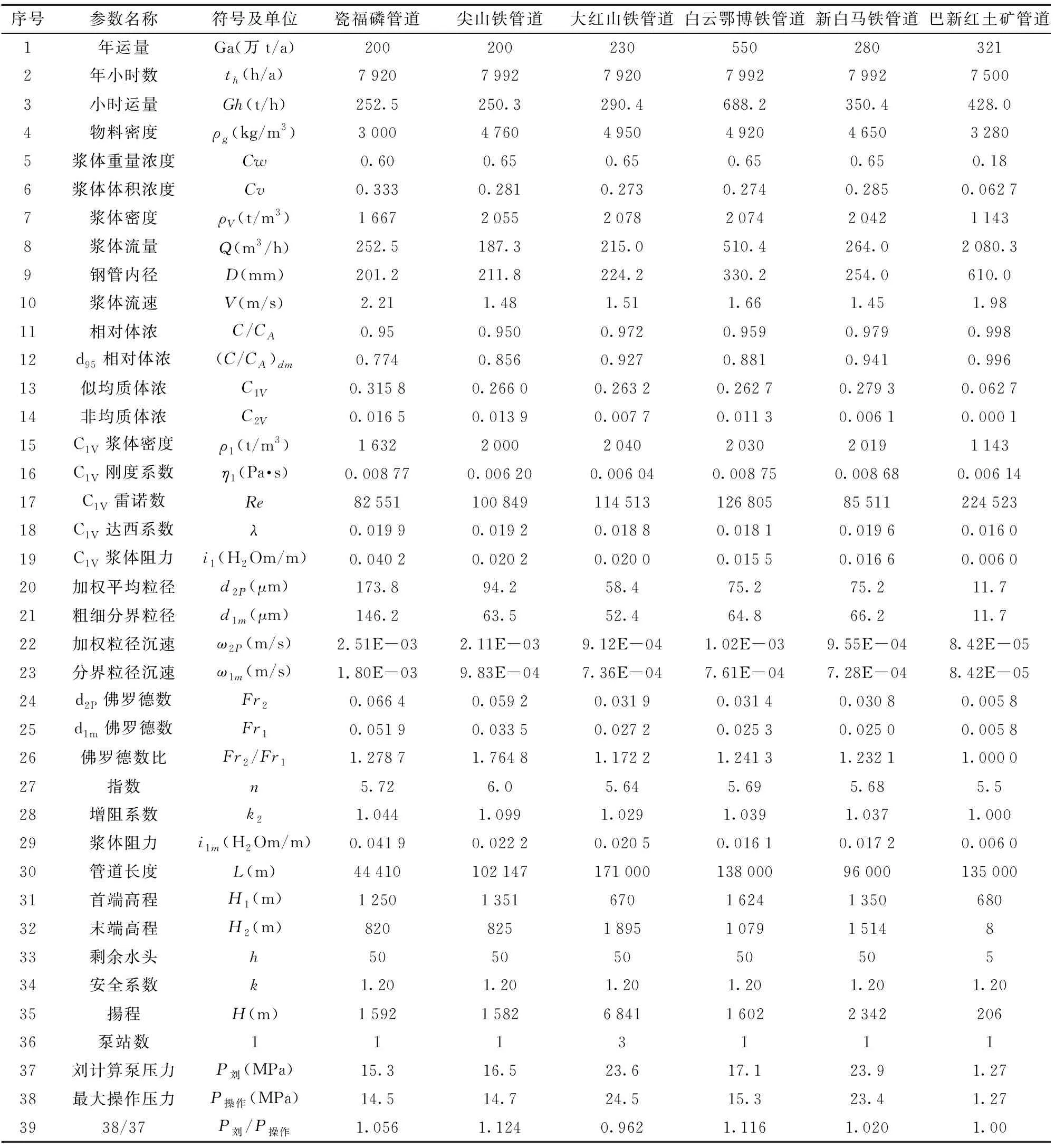
表2 对增阻系数法计算六条长距离管道阻力的验表

从表2可以看出,采用增阻系数法计算六条长距离管道阻力见序号29,计算压力见序号37,最大操作压力见序号38,38/37分别是1.056、1.124、0.962。1.116、1.020、1.000,平均值为1.046 4,最大为1.124 3,最小值为0.962,计算结果相近。

6 结论