基于粗糙集理论的矿柱稳定性影响因素敏感性分析

孙文勇, 王 明(四川鑫科创安安全科技有限公司, 四川 绵阳 621000)

1 前言

房柱采矿法具有采准切割工程量小,矿房生产能力大,通风条件优越,生产工作组织简单等优点,是开采浅部水平和缓倾斜矿体最有效的采矿方法之一,被矿山企业广泛应用[1]。但采用房柱法开采后往往会在采场留下大面积采空区,给采场留下较大的安全隐患。针对这一问题,通常采用预留矿柱来维持采场采空区的稳定。而影响矿柱稳定性的因素较多,研究矿柱稳定性影响因素敏感性,确定各因素对矿柱稳定性的影响程度对于矿山矿柱安全管理具有重要的理论意义和实际意义。

目前,矿柱稳定性影响因素敏感性的研究方法主要有理论分析[2-3]、算法优化[4-5]及数值模拟[6]等。另外,不少学者对矿柱稳定性影响因素进行了探究余佩佩等人[7]引入数量化理论Ⅱ建立了地下矿山矿柱稳定性判别模型,该模型能较好的判别预测矿柱稳定性。张钦礼[8]等人建立了尖点突变模型,分析采场空区能量释放机理,研究表明了矿柱的应变软化特性和刚度比是导致系统失稳的主要因素;过江[9]等人基于普氏理论分析了矿柱的承载机理,根据矿山采场内矿柱失稳的充分条件和必要条件推导得出采场内矿柱极限宽度值的计算方法并对影响矿柱宽度的主要因素进行了研究。李坚玲等[10]采用正交试验的极差分析方法,分析了矿柱稳定性影响因素的敏感性,矿柱稳定性影响最显著的因素为矿房宽度。闫国斌等[11]利用层次分析法研究得到影响矿柱稳定性的主要因素为矿柱形式和尺寸以及矿柱间距、爆破因素、矿柱岩性等。叶海旺等[12]基于极限强度理论并结合数值模拟方法研究了矿柱间距、矿柱埋深、矿柱尺寸等因素对矿柱安全系数和稳定性的影响规律。陈偶等[13]运用ANSYS数值模拟方法对地下矿山水平矿柱的稳定性进行了分析,并提出了水平矿柱稳定性系数的评价指标,影响矿柱稳定的关键外部因素是水平地应力。

粗糙集理论是一种对数据进行分析和推理进而发现隐含的知识、揭示潜在的规律的方法。传统的矿柱稳定性影响因素敏感性分析评价方法多以定性分析为主,或是将其简化为确定性问题来分析,从而造成分析结果的偏差。粗糙集理论能克服传统赋权法主观性较强、所得结果与实际情况相悖的缺点,在各领域得到了广泛的应用[14-15]。因此,本文将粗糙集理论引入到矿柱稳定性影响因素敏感性确定当中,利用数据预处理方法对设计数据进行离散化处理,运用知识约简方法计算出影响矿柱稳定性各因素的权重,从而确定出影响矿柱稳定性最显著的因素。

2 工程背景

四川某锰矿位于四川盆地北部山地,龙门山脉南西缘,属深切割中山构造侵蚀地貌,区内地势陡峻,总体呈北高南低之势。矿区地层、构造简单,无岩浆活动。

矿区内共圈定三条铁锰矿体,矿体分布于寒武系下统邱家河组的炭硅质板岩中,矿体呈层状产出。矿体直接顶板岩性主要为褐灰黑色薄层状含铁锰碳硅质板岩、灰色、灰黑色薄层状～中厚层状含炭质板岩。矿体直接底板为灰黑色薄层状～中厚层状含铁锰炭质板岩、灰黑色炭硅质板岩、褐灰色薄层状～中厚层状变质砂岩。多数围岩与矿层界线清楚,局部有渐变过渡关系。

矿山前期采用平硐开拓、无轨矿用胶轮车运输矿石的地下开采方式。根据矿山地形、地质条件和矿体埋藏情况,矿层为缓倾斜矿床,因此矿山决定采用房柱采矿法回采矿石,使用YT-28型凿岩机凿岩爆破落矿,崩落的矿石采用耙渣机将矿石装入矿车内,然后由矿用胶轮车经主运输巷道运至地面临时堆存。

房柱法采矿的特点是在矿房中布置规则矿柱,以支撑顶板围岩,使人员在空场下顺利完成多项作业。矿山开采多年现已形成部分采空区,随开采工作的推进,采空区显然会逐渐扩大,对地面稳定性影响将进一步加大。在开采过程中,为不使地表塌陷,设计不对采空区矿柱进行回采,因此,为了保证采场的安全性,需要探究矿柱稳定性影响因素的显著性。

3 矿柱安全系数

3.1 矿柱载荷

确定矿柱载荷是矿柱稳定性分析工作的前提,目前,对于矿柱载荷问题,应用较为广泛的是矿柱的面积承载理论,根据该理论,矿柱所承受的载荷是其所支撑顶板范围内直通地表的上覆岩柱的重力[16]。矿柱的底面积S为按矿柱分摊的开采面积与矿柱自身面积之和,因此,矿柱的平均应力可根据式(1)进行计算。

(1)

式中,γ为岩石容重;h为埋藏深度;W0、WP分别为矿房和矿柱的宽度。

3.2 矿柱强度

目前广泛应用的强度计算公式为

(2)

式中,S1为矿岩的强度参数,需根据矿柱布设方式而定。α为常数,取值根据矿柱的宽高比值而定,当宽高比大于5时,α=1.4,而当宽高比小于5时,α=1.0。

3.3 安全系数计算方法

在对矿柱稳定性影响因素进行敏感性分析时,通常需要考虑以下因素;① 采场埋深(H);② 矿房宽度(Wo);③ 矿柱宽度(Wp);④ 矿柱高度(h);⑤ 矿体的单轴抗压强度(σc);⑥ 上覆岩层容重(γ);⑦ 矿柱长度(Lp);⑧ 矿柱长度方向的间距(Lo)。

矩形矿柱安全系数为

(3)

当矿柱的形状为正方形时,矿柱安全系数的公式可简化为

(4)

4 矿柱稳定性影响因素敏感性分析

4.1 粗糙集理论

4.1.1 粗糙集

粗糙集是由Z Pawlak提出的对不完整、不确定知识的研究方法,包括对数据的处理、表达和归纳。它是一种属性数据集合,该方法的研究对象是由一个多值属性集合描述的一个对象集合[17]。粗糙集理论在数据挖掘与处理复杂信息上具有明显优势。

4.1.2 信息系统

粗糙集理论可表示为,信息系统S(U,A),U={u1,u1,…,u|U|},U、A均为有限非空集,其中U={u1,u1,…,u|U|},表示论域,u|U|称为对象;A={a1,a1,…,a|A|}表示为属性;现定义每个a∈A,存在一个映射a:U→a(U),为属性a的值域,有A=C∪D,C∩D=φ,S(U,A)作为决策表,C为条件属性,D为决策属性。

4.1.3 上近似、下近似

假定集合X和Y,P和Q与X和Y近似于等价关系。设RXY是XY上任意二元关系,又设I=PR是不分明关系的积,则R的I+上近似和I-下近似分别被定义如下

I*(R)={(x,y)∈XY:I((X,Y))∩R≠∅}

(5)

I*(R)={(x,y)∈XY:I((X,Y))∈R

(6)

上近似和下近似的差为

BNI(R)=I*(R)-I*(R)

(7)

式(7)为R的边界线区域。下近似又称为R的I正区域,被记成POSI(R)=I*(R)。

4.1.4 不可分辨关系

P为条件属性C的子集,则由P决定的不可分辨关系IND(P)为

IND(P)={(x,y)∈U×U/∀a∈P,f(x,a)=f(y,a)}

(8)

式中,f(x,a)表示论域元素x∈U关于属性a的取值;不可分辨关系IND(P)构成了对论域U的一个分类,记作U/IND(P)。

4.1.5 知识约简

知识约简是在保持各个元素分类能力不变的条件下,删除其中的重复元素。设R是一个等价关系族,r∈R。如果IND(P)=IND(R-{r}),则称r在R中是可被约去的知识,如果P=(R-{r})是独立的,则P是R的一个约简。

4.1.6 属性重要性

P和Q分别为条件属性C和决策属性D的一个子集,则:

(9)

其中:|U|表示元素的个数;|POSp(Q)|表示POSp(Q)中元素的个数。

属性子集CiC关于D的重要性定义为

σD(Ci)=γC(D)-γC-C1(D)

(10)

σD(Ci)的值越大,表明相应属性的重要性越大;反之,重要性越小。

4.2 矿柱稳定性影响因素敏感性

根据四川某锰矿的现场实际条件,同时结合空场采矿法的特点,本文选取矿房宽度、矿柱高度、抗压强度、矿柱宽度、上覆岩层容重、埋深6项指标作为矿柱稳定性的影响因素。随后,根据矿山地质特征及矿体赋存情况,设计得到25组影响因素数据见表1,将其离散化得决策表,见表2。其中各论域U={1,2,3,4,5,…,25},条件属性集C={C1,C2,C3,C4,C5,C6},决策属性集D={D1,D2},C1为矿房宽度,C2为矿柱宽度,C3为矿柱高度,C4为抗压强度,C5为上覆岩层容重,C6为埋深,按式(4)计算得到矿柱安全系数D1,D2为矿柱稳定状态(安全系数小于1.5,通常视为不稳定)。

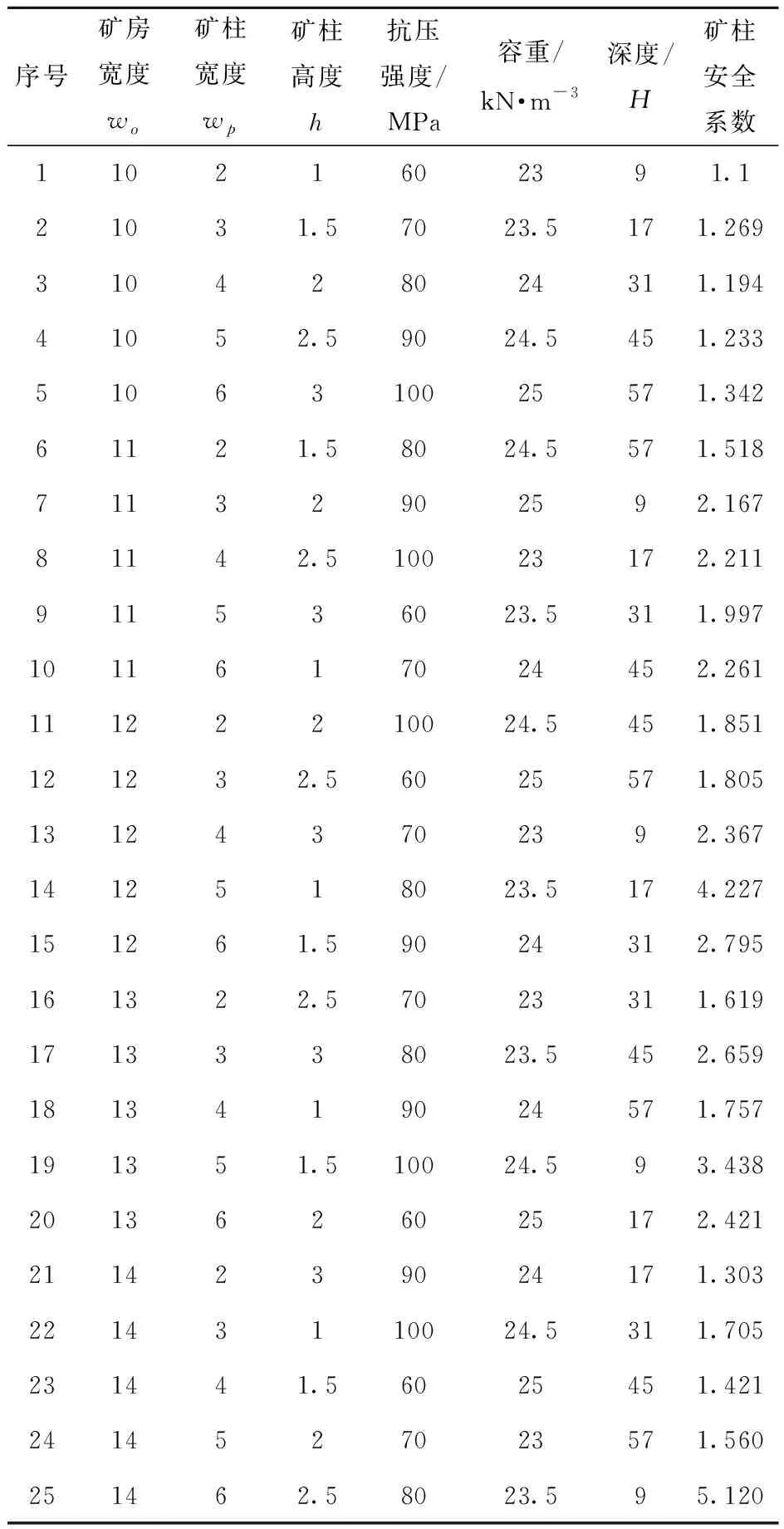
表1 四川某锰矿房柱法采场矿柱稳定性影响因素数据表

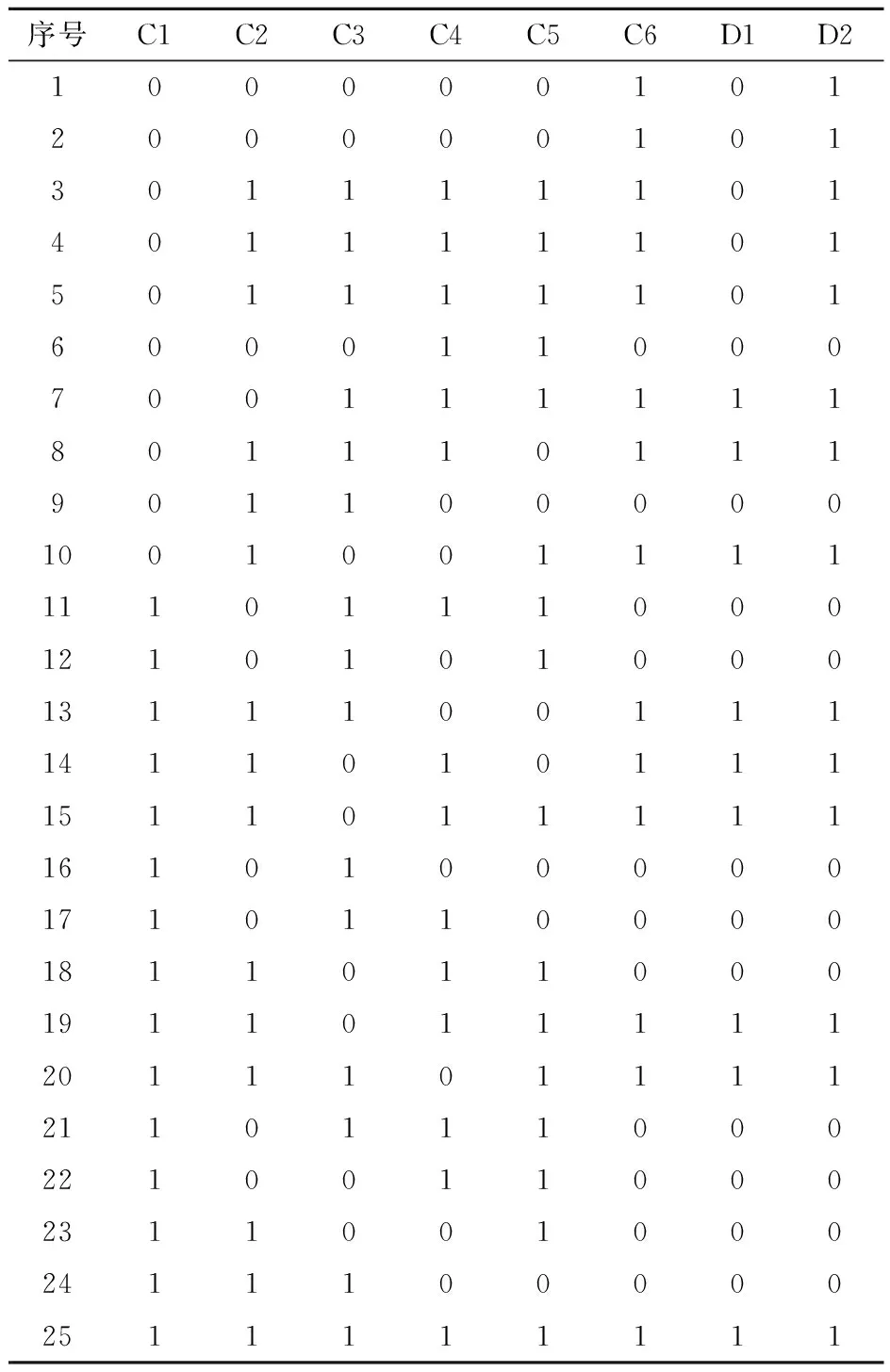
表2 四川某锰矿房柱法采场矿柱稳定性分析决策表

根据决策表将论域条件属性与决策属性分类:

U/IND(C)={1,2},{3},{4,5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18},{19},{20},{21},{22},{23},{24},{25}。

U/IND(D)={1,2,3,4,5},{6,9,11,12,16,17,18,21,22,23,24},{7,8,10,13,14,19,20,25}

去掉一个条件属性:

U/IND(C-C1)={1,2},{3,25},{4,5},{6},{7,21},{8},{9,13},{10,23},{11},{12},{13},{14},{15,19},{16},{17},{18},{20},{24}。

U/IND(C-C2)={1,2},{3,7},{4,5},{6},{8},{9},{10},{11},{12},{13,16},{14},{15,19},{17},{18},{20},{21,25},{22},{23},{24}。

U/IND(C-C3)={1,2},{3},{4,5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15,19},{16},{17},{18},{20},{21,22},{23},{24},{25}。

U/IND(C-C4)={1,2},{3},{4,5},{6},{7},{8,9},{10},{11,12},{13},{14},{15,19},{16},{17},{18,23},{20,25},{21},{22},{24}。

U/IND(C-C5)={1,2)},{3,8},{4,5},{6},{7},{9},{10},{11,17},{12},{13,20},{14.15},{16},{17},{18},{19},{20},{21},{22},{24},{25}。

U/IND(C-C6)={1,2},{3,4,5},{6},{7},{8},{9},{10},{11,21},{12},{13,24},{14},{15,18,19},{16},{17},{20},{22},{23},{24},{25}。

各因素关于决策属性的重要性:

POSC(D)={1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{16},{17},{18},{19},{20},{21},{22},{23},{24},{25}。

POSC-C{1}(D)={1},{2},{4},{5},{6} ,{8} ,{11},{12},{13},{14},{15},{19},{16},{17},{18},{20},{24}。

POSC-C{2}(D)={1},{2},{4},{5},{6},{8},{9},{10},{11},{12},{14},{15},{19},{17},{18},{20},{22},{23},{24}

POSC-C{3}(D)={1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{12},{13},{14},{15},{19},{16},{17},{18},{20},{21},{22},{23},{24},{25}。

POSC-C{4}(D)={1},{2},{3},{4},{5},{6},{7},{10},{11},{12},{13},{14},{15},{19},{16},{17},{18},{23},{20},{25},{21},{22},{24}。

POSC-C{5}(D)={1},{2},{4},{5},{6},{7},{9},{10},{11},{17},{12},{13},{20},{14},{15},{16},{17},{18},{19},{20},{21},{22},{24},{25}。

POSC-C{6}(D)={1},{2},{3},{4},{5},{6},{7},{8},{9},{10},{11},{21},{12},{14},{16},{17},{20},{22},{23},{24},{25}。

经计算,矿柱稳定性各因素条件属性重要性分别为0.381、0.285、0、0.095、0.048、0.2。由此可见,在影响矿柱稳定性的因素中,矿房宽度的影响最大,矿柱宽度、开采深度与抗压强度的影响次之,矿柱高度和上覆岩层容重的影响较小。

矿柱稳定性影响因素敏感性分析中,较为常用的算法为正交极差分析法,本案例中各因素极差值分别为1.381 4、1.309 6、0.559、1.194 8、0.55、1.242,该结果中矿房宽度极差值最大,对矿柱稳定性的影响最为显著,与粗糙集理论所得结果一致,同时也表明粗糙集理论可用于矿山矿柱稳定性分析工作当中。

5 结论

本文提出了基于粗糙集理论的矿柱稳定性影响因素分析方法,并在四川省某锰矿房柱法采场进行了应用。首先,结合采场工程实际情况确定了影响矿柱稳定性的主要因素和次要因素。随后,运用粗糙集理论对各影响因素进行了分析,确定了各影响因素对矿柱稳定性的敏感程度。得到如下结果:

(1)影响四川省某锰矿房柱法采场矿柱稳定性的因素主要包括矿体开采深、矿房宽度、矿柱宽度、矿柱高度、矿体的单轴抗压强度、上覆岩层的容重等。

(2)运用粗糙集理论对各影响因素进行了分析,四川省某锰矿房柱法采场矿房宽度对矿柱稳定性的影响最敏感。

(3)基于粗糙集理论的矿柱稳定性影响因素敏感性分析方法可以克服传统赋权法主观性较强、所得结果与实际情况相悖的缺点,研究结果可为矿山空场法采场矿柱尺寸优化与改进提供理论依据。