基于ESO 的水下机器人机械臂系统鲁棒模型预测控制

王红都,高 枫,黎 明,付东飞

(中国海洋大学 工程学院,山东 青岛,266100)

0 引言

为了精确执行复杂水下作业工作,通常会为自主水下航行器(autonomous undersea vehicle,AUV)[1-3]搭载水下机械臂,构成水下机器人机械臂系统(undersea vehicle manipulator system,UVMS)[4-6]。但水下环境的不确定性和UVMS 的强非线性和强耦合性,使得UVMS 完成跟踪预期轨迹变得具有挑战性,甚至不能保证系统稳定性。此外,UVMS 还需要满足扭矩、安全和机械等约束条件[7],否则会对UVMS 造成一定程度的损坏甚至故障。因此,设计具有良好抗干扰性能和满足约束条件的控制器对UVMS 非常重要。

UVMS 的建模与控制方面迄今已取得了很大的研究进展。Fossen[8]采用牛顿-欧拉公式建立了UVMS 运动学与动力学模型。Tarn 等[9]提出了一种新的基于拉格朗日方程和牛顿-欧拉公式的模型。UVMS 的抗干扰控制方面也取得了一定的研究进展。Lin 等[10]针对UVMS 提出了一种基于多观测器的滑模预设性能控制方法,利用扩张状态观测器和滑模干扰观测器来估计并提前进行补偿,最后采用滑模控制器进行控制,达到了良好的轨迹跟踪效果。Antonelli 等[11]用观测器来估计跟踪控制律中的系统速度,使UVMS 有效地跟踪期望轨迹并在跟踪性能与计算负荷中进行了权衡简化。为了进一步解决UVMS 中的末端执行器跟踪问题,Antonelli 等[12]还提出了一种新型的自适应控制律,将整体控制问题分解,制定模块化控制方案,减少了计算负担。Wang 等[13]采用离散时间延迟估计技术,提出了一种新的非线性鲁棒控制方案,对未知动力学进行了估计补偿,并获得闭环控制系统的期望动态特性,在任务空间中获得了0.064 m 的末端精度。然而,上述算法虽然能实现UVMS 良好跟踪性能,但无法保证约束条件的成立。

模型预测控制(model predictive control,MPC)作为一种最优控制策略,可以有效处理复杂系统的约束问题[14-25]。MPC 在每一采样时刻,根据当前获得的测量信息,在线求解一个有限时域开环优化问题,并将得到的控制序列的第1 个元素作用于被控对象。Shen 等[18]针对水下机器人系统,将路径规划与跟踪控制集成在一起,采用后退水平优化方案,利用b 样条进行路径规划并使用鲁棒模型预测控制器,通过仿真实验证明了其有效性,并分析了闭环系统的稳定性。Dai 等[19]提出基于管的鲁棒模型预测控制(robust MPC,RMPC),用于机器人机械臂系统的时变轨迹跟踪控制,对名义系统的约束条件进行收紧,MPC 在以名义系统轨迹为中心的管内驱动实际系统的轨迹。进一步提出了一种带有卡尔曼滤波目标观测器的鲁棒快速管模型预测控制,用于解决运动约束冗余UVMS 在存在建模不确定性、噪声和外部干扰情况下的移动目标抓取问题,并通过仿真实验验证了其有效性[20]。需要指出的是,现有的UVMS 的MPC 方法能够解决条件约束问题,但不能很好解决干扰抑制与补偿问题。

因此,文中旨在提出一种基于扩张状态观测器(extended state observer,ESO)的RMPC 方法,以同时解决条件约束与抗干扰问题。首先,定义忽略不确定因素和干扰的名义系统,在名义系统的基础上设计RMPC 算法。然后,使用ESO 来估计总干扰并提前进行补偿,以提高UVMS的系统鲁棒性和抗干扰能力。接着利用反馈线性化方法求出作用于真实系统的控制器,并进行稳定性分析。最后,通过仿真实验验证了其有效性。

1 UVMS 建模

1.1 动力学建模

文中采用的UVMS 结构如图1 所示,包括6 自由度的水下机器人和2 关节的机械臂,其动力学模型描述如下:

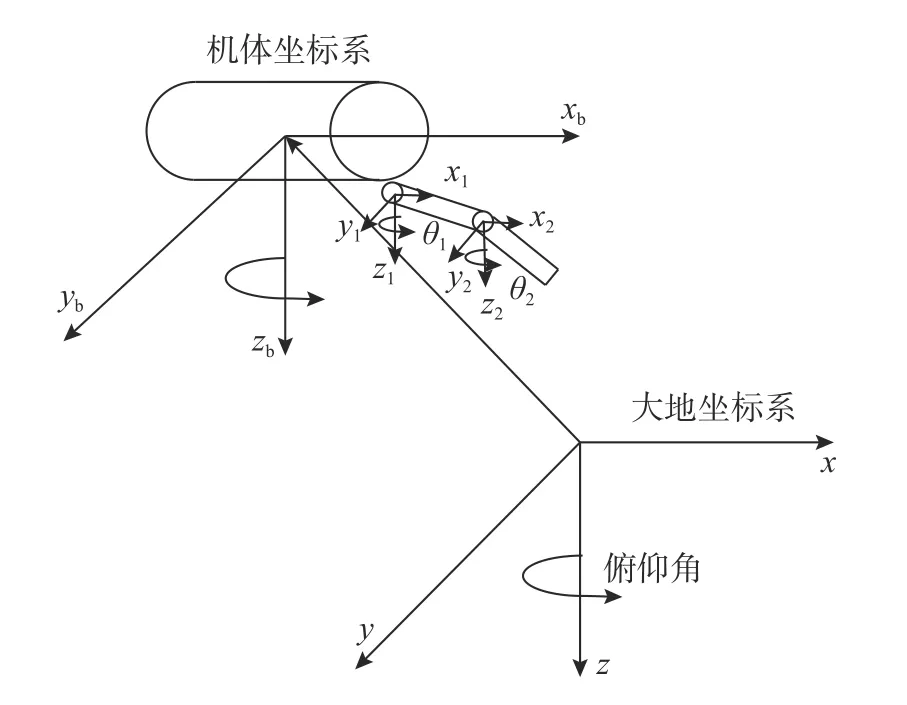
图1 水下机器人机械臂系统结构图Fig.1 Structure of UVMS

式中:q=[qv,qm]T包含水下机器人本体的位姿向量qv=[x,y,z,ψ]T和2个机械臂关节的角度qm=[θ1,θ2]T;ψ为机器人的偏航角;M(q)为系统的惯性力和力矩;C(q,)为 系统的科氏力矩阵;D(q,)为水动力阻尼矩阵;G(q)为 恢复力矩阵;F(q,)表示耦合作用;τc为输入力矩;τd1为未知干扰。

令γ=[u,v,w,r,p1,p2]T表示UVMS 在机体坐标系下的速度向量。由式(1)可得在机体坐标系下的系统动力学模型为

式 中:Mγ=JTMJ;Cγ=JTCJ+MγJ-1;Dγ=JTDJ;Gγ=JTG;Fγ=JTF;τγ=JTτc;J为机体坐标系与大地坐标系下的速度转换关系,有

考虑建模误差引起的不确定性因素,将参数矩阵分成已知与未知部分,即

由式(3)与式(5)可以得到模型

将式(6)改写为每个自由度的表达式为

令x1=q,x2=γ,x=[x1,x2]T,将系统模型以如下增广的状态空间形式描述:

1.2 误差动力学模型

令qR=[xR,yR,zR,ψR,θR1,θR2]T表示UVMS 的期望轨迹,其速度表达式为

进一步可得跟踪误差关系为

可分别表示为前馈控制与反馈控制,则知

详细推导见附录A。

在机体坐标系下,期望轨迹的动态方程为

对le=γ-vf进行微分,并与式(15)相结合得

其中

式中,Fu,Fv,Fw,Fr,Fp1,Fp2见附录B 式(63)～(68)。

结合式(15)与(17)得到增广的误差系统

在式(19)的零平衡点处,即当误差动力学状态为零,结合式(16),显然Fu=FuR,Fv=FvR,Fw=FwR,Fr=FrR,F1=F1R,F2=F2R,实际的控制输 入量与期望的输入量一致。如此可见,可以将期望轨迹的跟踪问题转化为误差系统(19)在平衡点的镇定问题,并可用MPC 实现目标镇定。

2 UVMS RMPC 设计

2.1 RMPC 算法

针对系统(10),忽略系统的不确定性与干扰,可以得到如下名义模型

则其误差动态模型为

设计代价函数

式中:T为预测时域;为阶段代价,其中Q为半正定权衡矩阵,R为正定权衡矩阵;是终端代价,其中P为正定终端权衡矩阵。

有限时域最优控制问题可以表示为最小代价函数问题

选取 δ ∈[t t+T],则

式中: Ω为终端区域;Ue为包含内部原点的区域,对系统的输入限制形式如下

误差控制与实际控制输入之间的关系为

其中

进一步选取终端区域 Ω=Ω1∩Ω2,其中Ω1:=,Ω2由式(32)定义。

整体系统满足以下约束关系:

2.2 反馈线性化控制设计

在MPC 滚动优化过程中,预测状态与实际系统状态会出现偏差,为了使实际系统状态与名义系统状态的误差状态量保持稳定,利用反馈线性化控制设计如下控制器:

式中: ς1∈[t,t+δ];(δ|t)为最优名义输入;(δ|t)为最优名义状态;Ke=[K1K2],其中

选择ki1<0,ki2<0,且+4ki1>0,i=1,···,6。表示实际状态与名义状态的误差状态,则可知

将控制器(34)代入(36)中,再结合式(10)与(20),得到

2.3 ESO 设计

ESO可以根据系统的输入输出估计出控制器的反馈,同时可以将UVMS 内部模型的不确定项、耦合项、模型内部干扰及水下外部干扰等视作一个总的干扰,对这个总扰动进行估计并提前在控制部分进行补偿。因此,对于系统内部与外部的参数摄动与时变干扰都可以进行有效补偿,提高了系统的鲁棒性。

定义f1=γ,f2=τd,将系统模型(3)表示为

针对式(38),构造如下ESO

ESO 的补偿控制输入项

式中,eob=f1-z1。z1,z2为f1,f2的估计值。进一步可得

进一步可知

式中,λmax表示的最大特征值。可知,当t→∞时,xd(t)→0。

2.4 整体控制器设计

整体控制器包括2 个部分,一个是对通过优化问题(24)求优后的最优名义控制输入进行反馈线性化的控制输入部分(34);另一个是ESO 对系统干扰的估计后,为进一步抵消干扰,对控制输入的补偿部分(40)。作用于实际系统的整体RMPC 控制律为

至此,RMPC 整体的算法流程图如图2 所示。

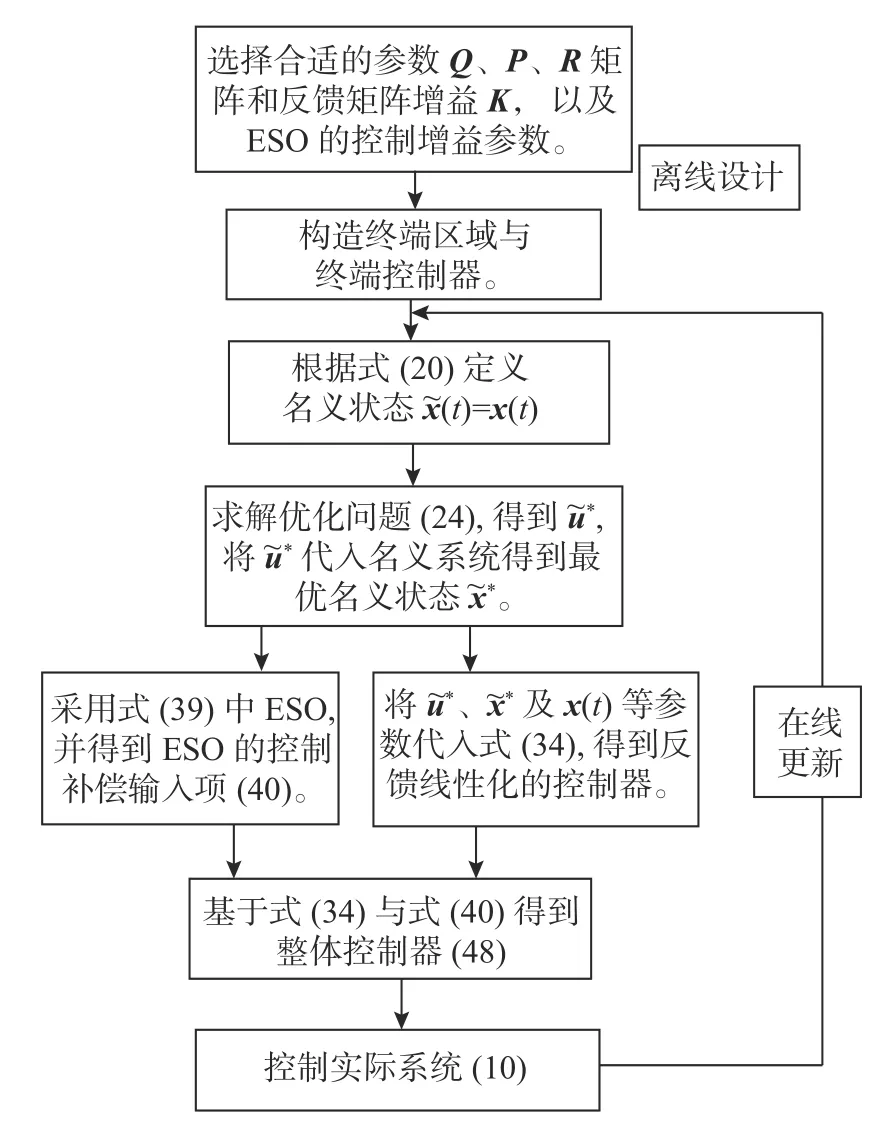
图2 鲁棒模型预测控制算法流程Fig.2 Robust model predictive control algorithm flow

2.5 可行性与稳定性分析

首先对优化问题的可行性进行简要分析,给出如下引理。

引理: 若开环优化问题(24)在t=0 时刻可行,意味着在t≥0时刻都是可行的,且系统状态满足终端约束。

证明: 假设在某一时刻t优化问题存在1 个可行解,则该名义最优控制输入满足输入约束条件,且将控制输入作用于系统生成的最优名义状态也满足状态约束,系统状态轨迹末端进入终端域。在t+δ时刻优化问题的初始状态也是t时刻的最优名义输入,即x(t+δ)=(t)。

在求解下一时刻的优化问题时,构造如下候选控制输入

该函数包括最优名义控制输入项及终端局部反馈控制项。对于第1 部分的控制输入而言,由于t时刻最优名义控制输入满足控制约束且系统状态也满足状态约束,显然t+δ时刻也是满足的。第2 部分的局部反馈控制器控制的终端区域是1 个不变集,也是满足约束条件的。综上,可行性的分析是具有递推性的。

然后对系统稳定性进行分析,选取最优值函数作为李雅普诺夫函数,考虑2 个时刻间的差值:

所以∆J≤0,由此得出系统是渐进稳定的。

3 仿真实验

3.1 参数选取

选取采样间隔为0.01,Mx=147,My=147,Mz=147,Mψ=8,Im1=10,Im2=10,Xu=0,Yv=0,Zw=0,Nr=0,Du=-148,Dv=-148,Dw=-148,Dr=-180,Dm1=Dm2=5。机械臂长度为 0.15 m,预测时域为8 ς,Q=0.4I12,R=0.01I4。将比例-积分-微分(proportion-integral-differential,PID)控制器的比例、积分和微分参数分别设定为

选择2 种工作场景:

且2 种场景下的外部干扰分别给定:

3.2 结果分析

在仿真阶段,将PID 和非奇异终端滑模控制器(non-singular terminal sliding mode controller,NTSMC)进行对比,仿真结果如图3～8 所示。在工况1 下,航行器按照预定的轨迹进行运动,整个过程中机械臂关节角度保持不变。为了与文中所提出的RMPC 进行对比,采用了传统的PID 控制器与SMC 分别对UVMS 进行控制。图3 给出了在不同控制器作用下,UVMS 本体在工况1 下的三维跟踪情况。从图3 中可以看出,基于ESO 的RMPC 有很好的抗干扰效果与跟踪效果。图4 左边一列给出了各个自由度上轨迹跟踪情况,右边给出了相应的跟踪误差。从图4 中可知,在文中方法作用下,航行器每个自由度都具有较好的跟踪效果,且机械臂可以保持在特定的角度,航行器与机械臂的跟踪误差都趋于稳定。图5 展示了ESO 对每个自由度上总干扰的估计情况,从中可以看出,ESO 可以较为准确地估计干扰,其中黑色虚线表示i(i=1,···,6)个自由度上的总干扰。

图3 工况1 下UVMS 本体三维跟踪情况Fig.3 The 3D tracking situation of UVMS in case 1

图4 工况1 下轨迹跟踪情况Fig.4 UVMS tracking situation for case 1

图5 工况1 下ESO 干扰估计情况Fig.5 The situation of disturbance by ESO in case 1

在工况2 下,机械臂不再保持特定的关节角度,在航行器小范围的运动下,机械臂按照期望轨迹进行运动。图6 表示UVMS 本体在工况1 下的三维跟踪情况,从中可以看出,在航行器按照期望轨迹进行小范围移动时,RMPC 方法相比于其他2 种控制器仍具有更好的跟踪与抗干扰效果。图7 的左右2 列分别为各个自由度上轨迹跟踪情况与跟踪误差,从中可以看出,在RMPC 作用下,每个自由度都拥有良好跟踪性能,且机械臂进行工作时可以很好地跟踪期望轨迹,且跟踪误差是收敛的。图8 给出了工况2 下ESO 对每个自由度上总干扰的估计情况。

图6 工况2 下的UVMS 本体三维跟踪情况Fig.6 The 3D tracking situation of UVMS in case 2

图7 工况2 下UVMS 跟踪情况Fig.7 UVMS tracking situation for case 2

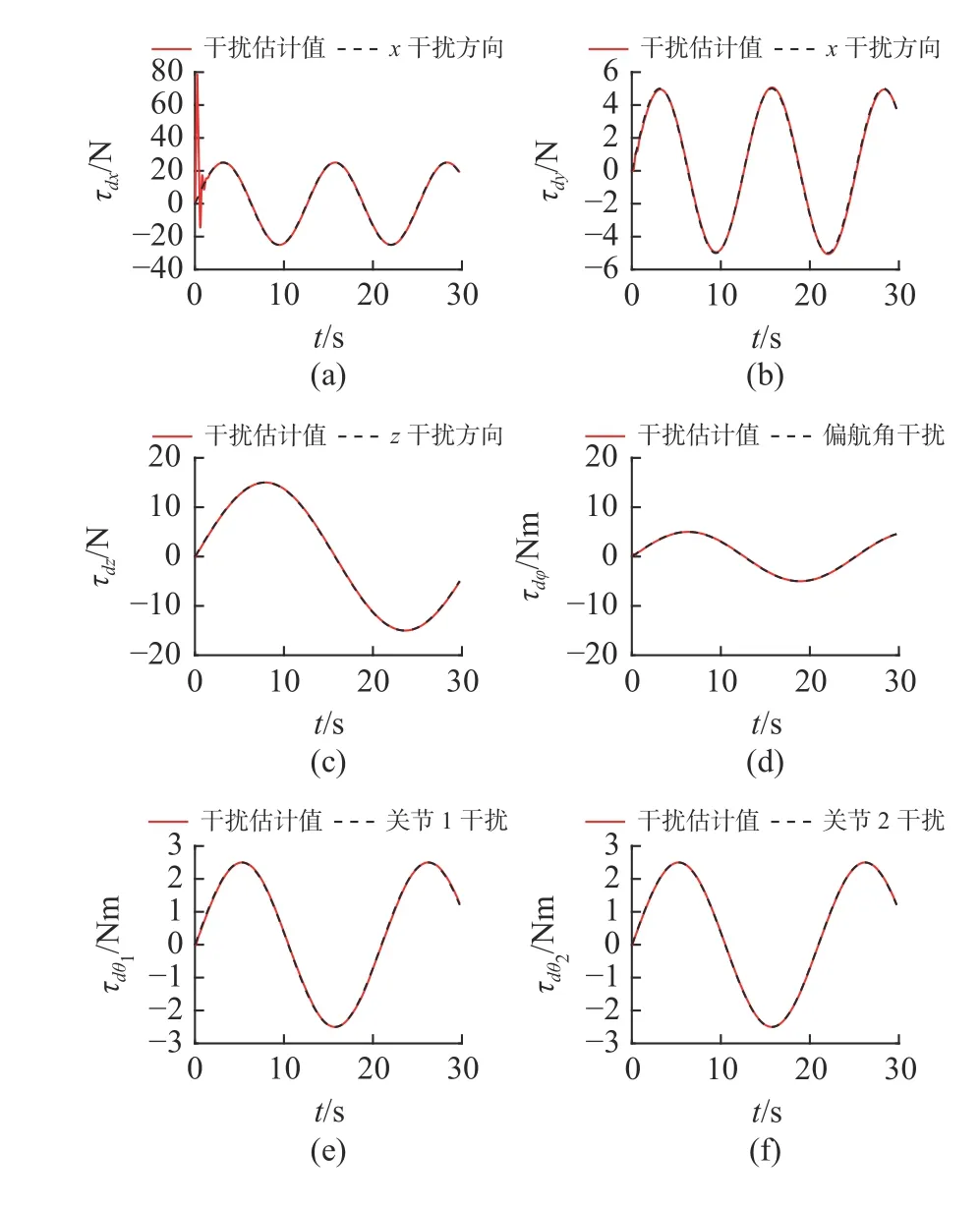
图8 工况2 下ESO 干扰估计情况Fig.8 The situation of disturbance by ESO in case 2

为了进一步对比各个控制器的控制效果,利用每个自由度跟踪误差的均方根(root mean square,RMS)指标进行数值比较,如表1 与表2 所示。表1显示的是工况1 下各控制器对期望轨迹的跟踪误差情况,表2 显示的是工况2 下每个控制器对期望轨迹的跟踪误差情况。可以明显地看到文中所提算法作用于每个自由度的误差RMS 更小,跟踪效果更好。

表1 工况1 下各控制器的跟踪误差RMS 指标Table 1 The tracking error of each controller in case 1

表2 工况2 下各控制器跟踪误差RMS 指标Table 2 The tracking error of each controller in case 2

4 结束语

文中针对UVMS 提出了一种基于ESO 的RMPC 方法。首先对名义模型进行RMPC 算法设计,结合ESO 对干扰提前进行估计并进行补偿,在此基础上利用反馈线性化方法求出作用于真实系统的RMPC 控制器,最后通过仿真实验验证了算法的有效性。未来将进一步研究多关节UVMS的RMPC 跟踪方法并应用于实际UVMS 系统,并开展相应的水池试验或湖试。

附录A

附录B