滚筒内三元颗粒混合的离散元模拟

荣文杰， 瞿林涛， 李嘉钰， 李宝宽

（1.东北大学 冶金学院， 沈阳 110819； 2.矿冶过程自动控制技术国家重点实验室， 北京 102628）

滚筒是在冶金工业中被广泛应用的颗粒物料处理设备，如回转窑、干燥机等［1］.以冶炼镍铁合金工艺的回转窑为例，在生产过程中，红土镍矿、石灰石和烟煤等颗粒状材料进入回转窑后，会随着窑体转动而不断翻滚.但由于这些颗粒物料存在形状、尺寸、密度、表面粗糙度等多方面的差异，颗粒在运动过程中呈现出混合与偏析的现象.不同颗粒的混合程度直接影响物料间的热质传递过程，进而影响产品质量，因此滚筒内的颗粒混合与偏析过程一直备受研究者们的关注.

近年来，很多学者针对滚筒内颗粒混合与偏析过程开展了物理实验和数值模拟研究［2］.与流体混合类似，颗粒混合的3 个主要机理为对流混合、扩散混合和剪切混合［3］.不同物性的颗粒在混合过程中会出现偏析现象，其中颗粒直径和密度的差异是引起颗粒偏析的主要原因.由颗粒直径不同而引起的颗粒偏析现象的机理包括渗透、流动和振动，而浮力是不同密度颗粒偏析的机理.离散元模型（discrete element model， DEM）是常用的数值模拟方法，该模型在计算过程中可以追踪到每个颗粒的位置和速度，从而得到详细的颗粒信息.由于它具有能够预测实验难以测量的颗粒信息，以及比连续性模型更直观显示颗粒的优势，故得到了广泛的应用［4］.Zhu 等［5-6］对DEM 的相关理论发展及其在颗粒系统的应用进行了总结，他们认为DEM 是研究颗粒运动行为的有效方法.Yang 等［7］应用DEM 对不同转速滚筒内同一直径颗粒的宏观和微观行为进行研究，展示并对比了多种颗粒流动状态.胡陈枢等［8］采用DEM 对滚筒内不同直径二元颗粒的运动过程进行模拟，提出了表观混合指数和动态混合指数的概念，并将它们用于计算颗粒的径向混合程度.Xie 等［9］通过研究滚筒内颗粒床的活动区发现，随着弗劳德数的增大，活动区的颗粒速度逐渐增加.葛良等［10］采用DEM 模拟波形滚筒内颗粒混合过程发现，在波形滚筒内使用较低的转速将达到与圆形滚筒较高转速下相同或相近的颗粒混合程度.Fernandes等［11］对颗粒的摩擦系数、恢复系数、杨氏模量和泊松比等输入参数进行不确定性的量化研究，他们发现摩擦系数是滚筒内颗粒流动最主要的影响参数.Zhang 等［12］研究了具有提升板的滚筒内颗粒运动情况并与PIV 测量结果进行对比，结果表明颗粒速度随滚筒转速的增加及填充比的降低而增加.Dury 等［13］研究了滚筒内不同直径颗粒的径向偏析与滚筒转速的关系，提出了描述最终偏析数量和偏析速度的参数.董彦龙［14］研究了滚筒内不同密度颗粒的偏析过程，发现密度比越大，颗粒偏析越明显.Xu 等［15］研究了颗粒尺寸、密度和摩擦对滚筒内颗粒混合的影响，结果表明颗粒尺寸和密度对颗粒混合的影响较大，但对颗粒摩擦的影响较小.Li 等［16］对椭圆柱形滚筒内不同颜色的颗粒混合过程进行研究，他们发现在椭圆柱形滚筒内，转速低时颗粒的混合得到改善，转速较高时颗粒在水平方向上的偏析得到加强.赵永志等［17］通过控制滚筒的转速和填充比分别得到了月亮模式和太阳模式的颗粒径向偏析.Maione 等［18］还对滚筒内圆柱形颗粒的轴向偏析现象进行了研究.上述研究展示了均匀或者二元颗粒在滚筒内的运动过程和混合及偏析现象，并揭示了不同性质颗粒的混合及偏析机理.

当前的研究大多针对均匀颗粒或者二元颗粒，然而工业中应用的颗粒物料往往更加复杂，一般是多种不同性质的颗粒混合在一起.因此，本文中针对不同直径的三元颗粒建立离散元模型，对3 种不同直径颗粒在同体积和同数量工况下的颗粒离散分布、颗粒床动态休止角及颗粒速度分布进行探究，以此开展多元颗粒混合过程的模拟计算，为研究更接近实际的滚筒内颗粒混合过程提供参考.

1 数学模型及计算条件

1.1 离散元模型

DEM 最早由Cundall 和Strack 在20 世纪70年代提出［19］，近年来逐渐得到广泛应用.DEM 利用牛顿经典力学方程，对相邻元之间因接触产生的作用力进行计算.每个单元受力后在合力和合力矩的作用下发生形变和位移，通过牛顿力学方程和运动定律的循环计算，就可以追踪到每个颗粒的位置和速度.离散单元接触模型主要有硬球模型和软球模型.硬球模型假设颗粒与颗粒之间的碰撞是瞬间发生的.软球模型则假设颗粒与颗粒之间发生的碰撞是在某个连续的时间范围内，通过重叠量的大小以及牛顿动力学定律来计算出颗粒间的接触力等状态参数.在软球模型模拟颗粒碰撞的过程中，将两个离散单元颗粒之间的碰撞作用在法向和切向方向都抽象为弹簧、阻尼器及滑动摩擦器的共同作用，通过弹性、阻尼及滑移的力学机理考虑颗粒间的相互作用.图1 为颗粒接触受力示意图.

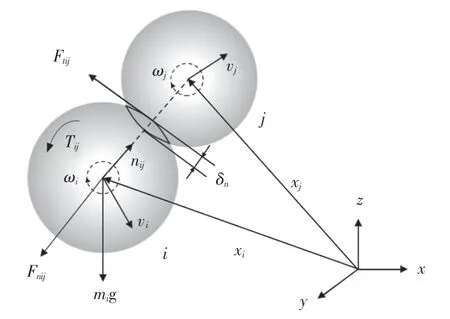
图1 颗粒接触示意图Fig.1 Schematic of two particles in contact

在时间t内，颗粒i的位置、线速度和角速度可依据牛顿定律进行计算.

式中：m，I，v，ω和g分别表示质量（kg）、转动惯量（kg·m2）、线速度（m／s）、角速度（rad／s）和重力加速度（m／s2）；xi表示颗粒i的位置；Fcnij和Fctij分别表示颗粒法向接触力和切向接触力（N）；Fdnij和Fdtij分别表示颗粒法向阻尼力和切向阻尼力（N）；Ttij和Trij分别表示颗粒受到切向力产生的扭矩和滚动摩擦力产生的扭矩（N·m）.DEM 广泛用于颗粒运动过程计算，详细的力和力矩计算公式可以参考文献［5-9］.

1.2 边界条件及模拟参数

本文中根据Parker 等［20］开展的滚筒内颗粒运动实验建立了三维滚筒离散单元模型.实验中滚筒长度为650 mm，但为了减少计算量，本文中模拟了一个长度为16 mm 的短滚筒，并为滚筒两端设置周期性边界条件来保证计算结果的可靠性，该方法已在文献［7］中得到证实.滚筒内放置的颗粒直径为3 mm，密度为2 500 kg／m3，颗粒之间的接触参数及模型其他参数见表1.滚筒内颗粒的运动模式随着滚筒转速不同一般分为6 种，即随着转速增加，依次呈现滑动、坍塌、滚动、倾泻、崩塌和离心.在实际生产中颗粒运动往往处于滚动模式，本文中研究的滚筒内颗粒运动在转速42 r／min时处于滚动模式.在计算过程中，颗粒在滚筒内的指定位置生成后受重力作用下落到底部，考虑到颗粒初始位置及分布并不影响最终的混合结果，颗粒生成位置设定为按空间坐标均匀分布.但是，为了保证颗粒位置和速度在初始状态是稳定的，当所有颗粒下落停稳后，设置滚筒开始旋转.滚筒转动6 圈后，颗粒运动呈现动态稳定状态.为了保证计算结果的可靠性，下文讨论的是滚筒旋转到8 圈以后的计算结果.

表1 模型参数Table 1 Parameters in model

为了完成模型验证，将单一直径颗粒的计算结果与实验结果进行对比.在此基础上，本文中进一步探究了直径为3，4，5 mm 的颗粒在同数量和同体积两种工况下的混合过程.主要原因如下：一方面是考虑到该颗粒体系仍然能够使用原计算网格；另一方面是考虑到渗透原理会导致不同直径颗粒在混合过程中出现偏析，颗粒直径差距过大时偏析规律显而易见，而三元颗粒在直径相近情况下的混合与偏析情况更值得研究.表2 列出了不同工况的颗粒数量.

表2 两种工况下的颗粒数量Table 2 Particle numbers under two working conditions

1.3 离散中心及离散半径

同一直径颗粒在滚筒内会呈离散分布，本文中定义“离散中心”来描述某一时刻同一直径颗粒在整个离散空间分布的中心位置.以建立的滚筒模型中心位置为三维坐标系原点，离散中心坐标公式如下所示：

式中：（xi，yi，zi）为某一直径的颗粒i在三维空间的坐标；ni为该直径颗粒个数；（）为离散中心在三维空间下的坐标.

以离散半径表示某直径颗粒距离其离散中心的平均值，可用此参数反映离散空间上颗粒群分布范围的大小.以R代表离散半径，其计算公式如下所示：

式中：n为颗粒总个数.

2 结果与讨论

2.1 模型验证

Parker 等［20］在滚筒内颗粒运动的实验中采用正电子发射粒子跟踪方法（positron emission particle tracking， PEPT），测量了不同转速下颗粒床动态休止角和颗粒沿颗粒床中心线的切向速度.本文中将转速为42 r／min 的模拟结果与实验结果进行对比，结果如图2 和图3 所示.由图可知，颗粒床动态休止角和颗粒切向速度结果分别与实验值吻合，该结果验证了模型的准确性.

图2 颗粒床动态休止角对比Fig.2 Comparison of dynamic angle of repose of particle bed

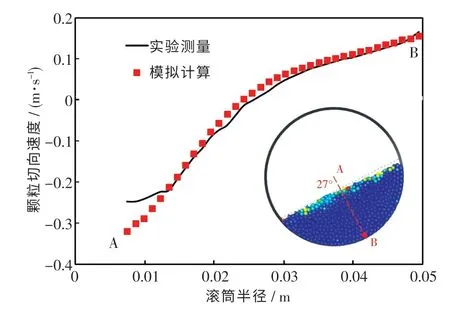
图3 颗粒切向速度对比Fig.3 Comparison of particle tangential speed

2.2 颗粒离散分布

根据前述定义，3 种不同直径颗粒在同数量和同体积两种工况下的离散半径如图4 所示.从图中可以看出，在滚筒旋转至6 圈后，颗粒运动状态基本稳定.在两种工况下，3 mm 颗粒离散半径最小，4 mm 颗粒离散半径居中，5 mm 颗粒离散半径最大.在同数量工况下，3 种颗粒的离散半径差距相当，约为0.005 m；在同体积工况下，5 mm 颗粒与4 mm 颗粒的离散半径差别明显缩小，4 mm颗粒与3 mm颗粒的离散半径差别略微增大.这是由于在同体积工况下，5 mm 颗粒的数量较少，而3 mm 颗粒的数量较多.

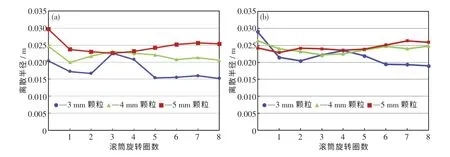
图4 两种工况下离散半径的变化Fig.4 Revolution of discrete radius under two working conditions

图5 更直观地展示了3 种颗粒在同数量工况下的整体分布及各直径颗粒的单独分布.从图中可以看出：3 mm 颗粒集中分布在颗粒床的内部区域；5 mm 颗粒大部分分布在颗粒床的外部区域，并几乎填满了整个外围部分；而4 mm 颗粒大部分填充在3 mm 颗粒与5 mm 颗粒之间.3 种颗粒形态分布大体上可看作为：5 mm 颗粒区域包裹4 mm颗粒，4 mm 颗粒区域包裹3 mm 颗粒，形成典型的“大包小”现象.

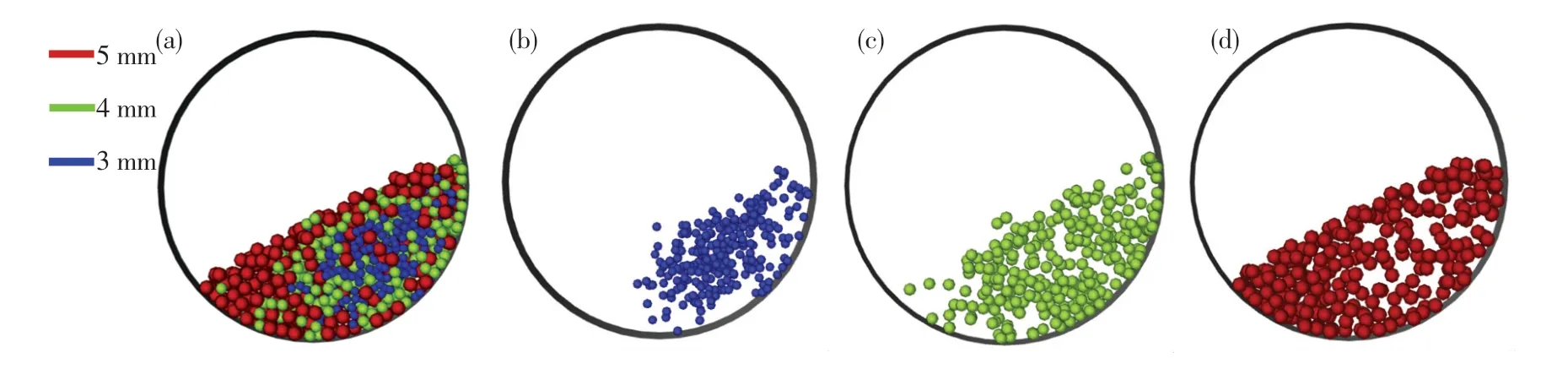
图5 同数量工况下的颗粒分布Fig.5 Spatial distribution of particles under the working condition of the same number

图6 展示了3 种颗粒在同体积工况下的整体分布及各直径颗粒的单独分布.从图中可以看出：3 mm 颗粒主要集中在颗粒床的内部区域，但由于其数量更多，有一部分颗粒向外围进行扩散；4 mm颗粒大部分分布在3 mm 颗粒群的外部，并在一定程度上挤占了本来5 mm 颗粒所处的外围区域；而5 mm 颗粒仍然大部分分布在颗粒床的外部区域.总的来说，3 种颗粒在空间上所占据的总体积是相等的，但依然出现了“大包小”的现象.

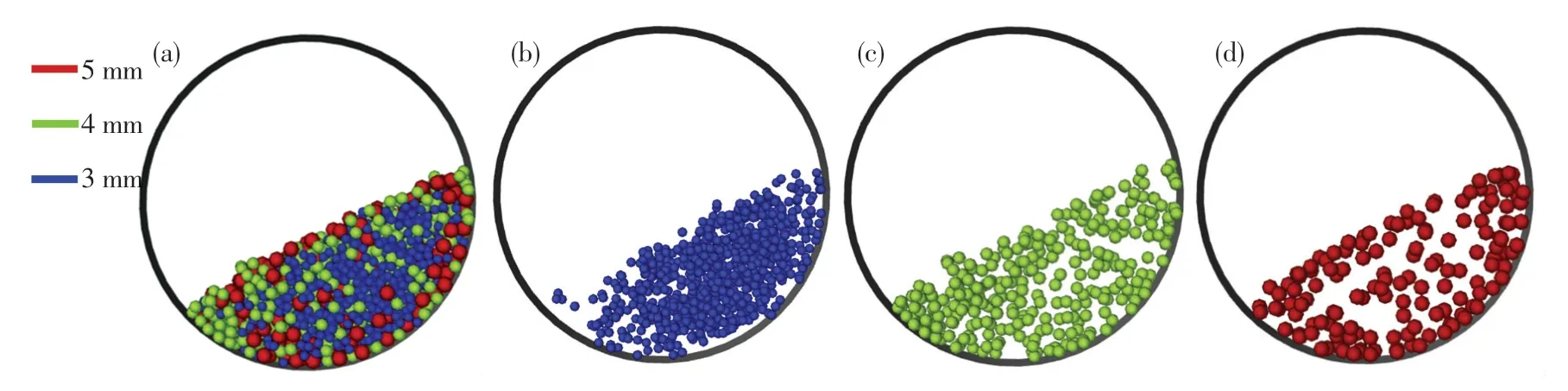
图6 同体积工况下的颗粒分布Fig.6 Spatial distribution of particles under the working condition of the same volume

2.3 颗粒床动态休止角

图7 示出了颗粒床动态休止角的计算结果.由图可知，在转速、填充比及颗粒接触参数一致的情况下，同数量工况下颗粒床动态休止角约为27°，同体积工况下颗粒床动态休止角约为28°，两种工况下的颗粒床动态休止角结果与Parker等［20］实验测量得到的颗粒床的动态休止角几乎是一致的.换言之，当颗粒在滚筒内处于滚动流态时，颗粒之间紧密接触，并且以颗粒床整体的形式一起随着滚筒的转动而运动.这也进一步验证了Mellmann 等［21］对滚筒内混合颗粒运动形态的研究结果：颗粒的大小及数量在固定的操作条件和接触参数下并不会影响颗粒混合后的床层形态.

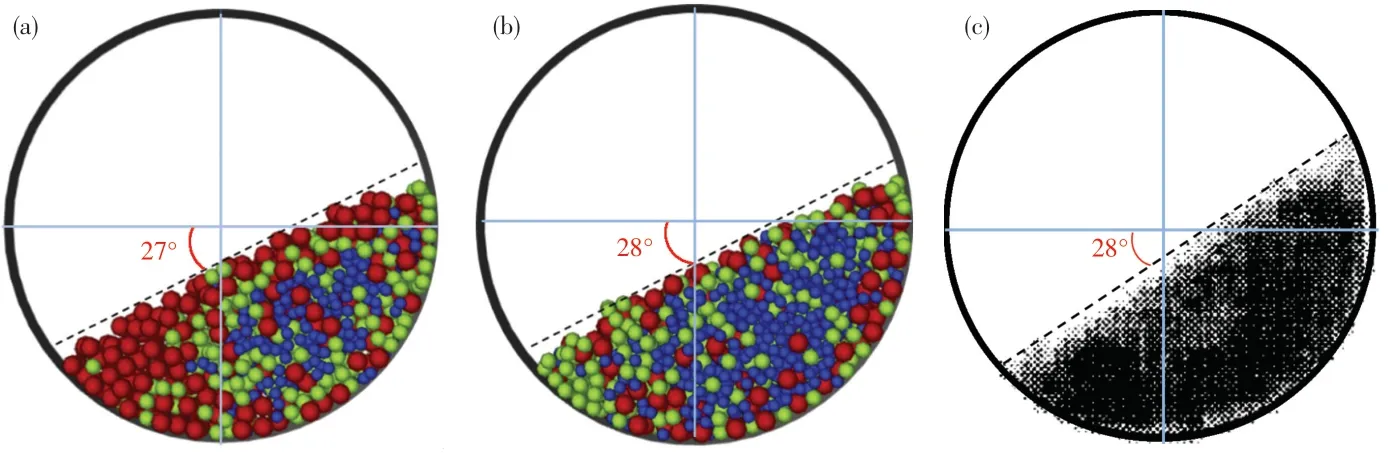
图7 颗粒床动态休止角对比Fig.7 Comparison of dynamic angle of repose of particle bed

2.4 颗粒速度分布

图8 展示了3 种颗粒在同数量工况下的整体速度分布及各直径颗粒的单独速度分布.从图中可以看出：颗粒床的倾斜表面较为平整，并有一层清晰可见的颗粒群从上往下快速滚落；与这些颗粒相比，其他颗粒则以较慢的速度在床层内部和底部循环进行爬升滚落；单一直径颗粒靠近颗粒床倾斜表面的数量越多时，它所占据的大速度颗粒就越多.因此，大部分位于外围区域的5 mm 颗粒群含有的大速度颗粒最多，4 mm 颗粒群次之，3 mm颗粒群中几乎没有速度较大的颗粒.同时，计算出各颗粒群速度的平均值如下：5 mm 颗粒群0.024 3 m／s；4 mm 颗粒群0.016 2 m／s；3 mm 颗粒群0.013 3 m／s.对于各颗粒群的平均速度而言，5 mm 最大，4 mm次之，3 mm 最小，这说明颗粒直径与该直径颗粒的平均速度呈正相关.

图8 同数量工况下的颗粒速度分布及其矢量形式Fig.8 Particle velocity distribution with the corresponding vector form under the working conditions of the same number

图9 展示了3 种颗粒在同体积工况下的整体速度分布及各直径颗粒的单独速度分布.从图中可以看出， 与同数量工况类似，颗粒床表面有一层清晰可见的颗粒群从上往下快速滚落.3 mm颗粒群整体速度偏低，而5 mm 颗粒群所含有的大速度颗粒变少，甚至没有4 mm 颗粒群所含有的大速度颗粒多.这是因为5 mm 颗粒群的外围空间被4 mm颗粒群挤占了一部分.各颗粒群平均速度结果如下：5 mm 颗粒群为0.019 2 m／s；4 mm颗粒群为0.016 9 m／s；3 mm 颗粒群为0.014 1 m／s.与同数量工况的结果类似，颗粒直径与该直径颗粒的平均速度呈正相关.

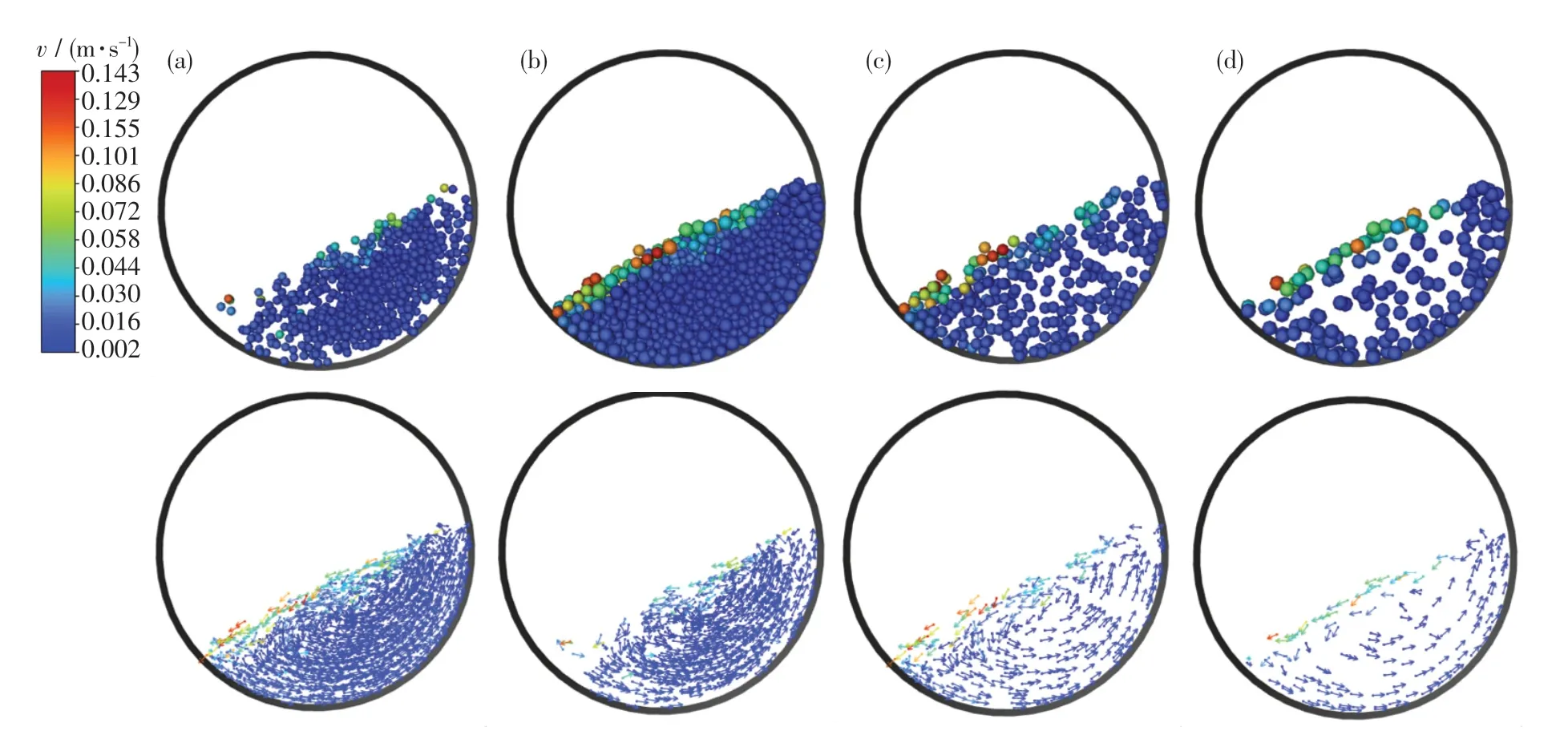
图9 同体积工况下的整体颗粒速度分布及其矢量形式Fig.9 Particle velocity distribution with the corresponding vector form under the working conditions of same volume

3 种直径颗粒在同数量和同体积两种工况下，全部颗粒的平均速度均为0.017 9 m／s.因此，当滚筒的操作条件和颗粒接触参数并未改变时，滚筒壁面传递给其内部颗粒的动量不受颗粒数量和直径的影响.

3 结 论

（1）3 种直径颗粒在同数量和同体积两种工况下，颗粒分布均出现了“大包小”的现象，颗粒的直径越大，对应的离散半径越大.在同数量工况下，3 种直径颗粒的离散半径差距相当；在同体积工况下，5 mm 颗粒的离散半径与4 mm 颗粒的离散半径差别明显缩小，4 mm 颗粒的离散半径与3 mm颗粒的离散半径差别略微增大.

（2）颗粒的直径大小及数量在操作条件和接触参数不变的情况下并不会影响到滚筒内颗粒床的动态休止角大小.

（3）3 种直径颗粒在同数量和同体积两种工况下，颗粒直径均与该直径颗粒的平均速度呈正相关关系；在同体积和同数量工况下颗粒的最大速度分别为0.143 m／s 和0.109 m／s；在两种工况下颗粒整体的平均速度均为0.017 9 m／s.